A semi-empirical approach to simulating the Dst index in global MHD models of Earth’s magnetosphere

pdf

1  Introduction

Dst指数 (Disturbance storm time index, 地磁暴时扰动指数) 是描述磁暴活动强度应用最广泛的指数，对于研究地磁扰动和磁暴具有重要意义。Dst指数的基本概念最初由Sugiura (1960)提出。它通过对四个低纬度观测台站测量的地磁场水平分量减去平静期的平均变化量而获得。选择这些观测台是为了最小化极光区电流 (auroral currents) 和赤道电急流 (equatorial electric currents) 的影响，并且它们的经度在全球范围内大致均匀分布。然而，Dst指数的时间分辨率仅为1小时，这对于描述某些地磁事件来说显得相对较长。作为一种替代方案，SYM-H指数 (Symmetric disturbance field index in H-component, H分量对称扰动场指数) 可被视为升级版的Dst指数，具有一分钟的分辨率，对于中度和强烈磁暴，其偏差通常小于20 nT。与Dst指数不同，SYM-H指数使用来自全球赤道区域经度均匀分布的六个低纬度和中纬度地面磁力仪台站的数据进行计算。

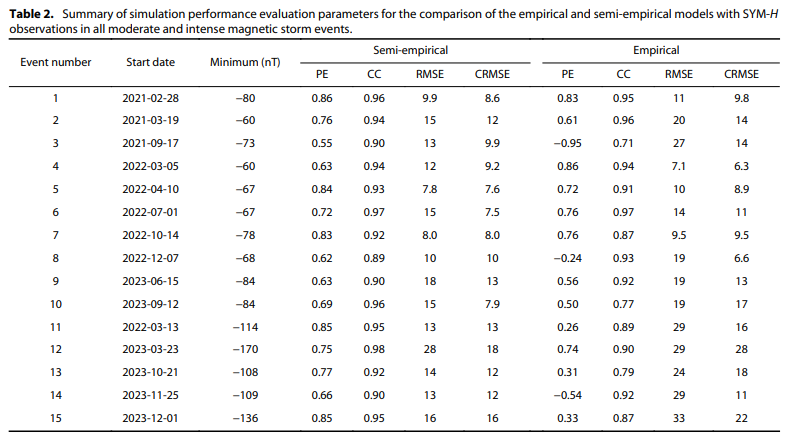
从物理意义上讲，Dst指数的大小是衡量赤道环电流 (equatorial ring current) 强度的尺度，通常可以反映磁暴的强度。Burton等人 (1975) 根据Dst指数的最小值将磁暴分为四个级别：最小值为−30至−50 nT的为小磁暴 (minor storms)，−50至−100 nT的为中等磁暴 (moderate storms)，−100至−200 nT的为强烈磁暴 (intense storms)，以及最小值超过−200 nT的为超级磁暴 (super storms)。

准确预测Dst指数对于磁暴及相关空间天气预报研究具有重要价值。人们已经开发了多种利用观测到的太阳风参数作为输入来预测Dst指数的方法。通常，它们可以分为三类，包括经验公式 (empirical formula)、机器学习方法 (machine-learning methods) 和基于物理的模型 (physics-based models)。其中，经验公式模型因其在数值实现上相对简单而被最广泛使用。在早期研究中，Burton等人 (1975) 提出了一个计算Dst指数的经验公式，该公式使用与太阳风参数相关的项作为微分方程中的系数，考虑了粒子从等离子体片 (plasma sheet) 注入内磁层 (inner magnetosphere) 的过程，并强调了行星际磁场 (Interplanetary Magnetic Field, IMF) 南向分量在计算中的关键作用。随后，该经验模型的一些扩展版本被推导出来并应用于相关领域，并且自Burton等人 (1975) 以来，已有许多基于此经验公式的研究 。

机器学习和神经网络技术已广泛应用于Dst指数的建模和预测 (Lu JY et al., 2016; Camporeale, 2019; Xu WW et al., 2023)。早在20世纪90年代，就有多次尝试利用神经网络预测Dst指数。Jankovičová等人 (2002) 采用全连接神经网络预测Dst指数，开发了一个能够利用ACE卫星数据提前两小时预测该指数的模型。Lundstedt等人 (2002) 研究了太阳风动压 (dynamic pressure) 变化和环电流注入的响应特性及衰减，发现当行星际磁场转向南向时，环电流注入速率与太阳风动压成正比。他们将这一发现应用于Dst指数的预测，提高了预测精度。Caswell (2014) 利用IMF分量、太阳风质子密度、等离子体速度和等离子体流压来提前一小时预测Dst指数。Lazzús等人 (2017) 引入了一个人工神经网络 (Artificial Neural Network, ANN) 模型，在1至6小时的提前时间内实现了更高精度的Dst指数预测。基于ANN模型的类似工作也已被开展，以期获得更好的预测精度和稳定性 (Lethy et al., 2018; Xu SB et al., 2020; Park et al., 2021)。

基于物理的模型通常通过求解描述环电流动力学的第一性原理方程来预测诱导产生的Dst指数。一些模型采用Dessler−Parker−Sckopke方程，将模拟环电流内的总能量转化为Dst，然后计算预期的Dst指数，其中还根据太阳风施加的动压纳入了磁层顶电流 (magnetopause currents) 的校正。Rice对流模型 (Rice Convection Model, RCM) 有效地描述了内磁层等离子体的电动力学 。它采用Hilmer和Voigt的磁场描述，结合Siscoe-Hill  或Weimer 电场模型。该模型基于磁层等离子体的压力梯度，使用Vasyliunas方程计算场向电流 (field-aligned current)。该电流进而确定电离层电位和电场，然后将其映射回内磁层以完成计算循环。这个过程使得计算环电流的能量成为可能。其他用于模拟环电流动力学的内磁层模型包括RAM-SCB (Radiation Belt Environment - Scattered Particle model with Self-Consistent magnetic field)、CRCM (Comprehensive Ring Current Model) 和WINDMI (Wave and Instability, Nonlinear, Driven, Magnetospheric-Ionospheric model) 模型。RAM-SCB是一个开源模拟代码，可模拟主要离子种类和电子在方位角、径向距离、能量、投掷角以及Dst指数等多个参数上的演化。另一方面，CRCM模型能够准确预测日冕物质抛射 (Coronal Mass Ejection, CME) 驱动的磁暴的Dst指数，但它低估了共转相互作用区 (Co-rotating Interaction Region, CIR) 驱动的磁暴的该指数，这种差异可能导致对总环电流能量高达一半的潜在高估，原因在于模拟静态磁场的局限性。最后，WINDMI是一个低阶、非线性环电流模型，能够生成地磁西向极光电集流 (geomagnetic westward auroral electrojet, AL) 指数和Dst指数的输出。

地球磁层的全球磁流体力学 (Magneto-HydroDynamic, MHD) 模型可以通过结合磁层中不同位置处的电流密度，利用毕奥-萨伐尔定律 (Biot−Savart formula) 计算地球中心的磁场扰动来模拟Dst指数。然而，这些模型无法有效模拟环电流，因为它们无法捕捉内磁层中带电粒子的漂移运动。因此，必须将内磁层模型集成到全球MHD模型中，才能更准确地模拟Dst指数。此类全球MHD模型的例子包括BATSRUS (Block Adaptive Tree Solarwind Roe-type Upwind Scheme)、OpenGGCM (Open Geospace General Circulation Model) 和LFM 。例如，BATSRUS模型有与RCM (De Zeeuw et al., 2004) 和CRCM 耦合的版本。当与内磁层模型集成时，BATSRUS显著提高了其在磁暴期间复现Dst值的能力，因为如果没有这个组件，它无法达到低于−30 nT的Dst值 。欧洲日球层预报信息资产 (European Heliospheric Forecasting Information Asset) 与OpenGGCM耦合时，展示了对地磁扰动指数的有效预测，从而增强了空间天气预报能力 。Rastätter等人 (2013) 对这些统计和基于物理的模型在计算Dst指数方面的性能进行了全面的回顾和分析。

不同于引入内磁层模型，本文尝试将经验公式集成到地球磁层的全球MHD模型中，以模拟Dst指数。本文结构如下：第2节介绍了计算Dst指数的方法，包括全球MHD模型和经验公式。第3节概述了分析中使用的具体事件和数据集。第4节展示了模拟结果，随后是对这些事件的讨论。最后，第5节总结了结论。

2. 方法 (Methodology)

2.1 全球MHD模型中的Dst指数 (Dst Index in a Global MHD Model)

Dst指数量化了低纬度地面普遍地磁活动的强度，并用于估计地球附近环电流的能量密度。 然而，其他磁层电流系统，如日侧磁层顶电流 (dayside magnetopause currents) 和夜侧磁尾电流 (nightside tail currents) 也会引起地面磁场扰动，它们可能对Dst指数有次要贡献。

本工作应用了PPMLR-MHD模型 (PPMLR-MHD model) 的修订版本。在该模型中，使用了一种为分解本征磁场而设计的HLL型黎曼求解器 (HLL-type Riemann solver) 的扩展，在MUSCL数值格式 (MUSCL numerical scheme) 中更新网格单元界面处的数值通量。在模拟过程中，任何给定网格点处的磁场B通过时变MHD方程在每个时间步长进行数值更新。磁层电流系统是通过持续的上游太阳风挤压引起的地磁场畸变直接计算得出的。然后，通过归一化关系 j=∇×B 获得电流密度 j，其中包含了大规模的磁层顶电流 (magnetopause currents)、场向电流 (field-aligned currents) 和磁尾电流 (tail currents)。然而，环电流 (ring currents) 并未产生，因为带电粒子的梯度和曲率漂移运动无法在单流体MHD近似中再现。

对于Dst指数，这里不考虑四个主要地磁观测台的确切位置；而是使用地球中心的磁场扰动来表示地面赤道面上的平均地磁扰动，并将对应的地磁扰动的南北轴向分量定义为Dst指数，遵循先前研究者在全球MHD模拟中采用的类似方法。使用毕奥-萨伐尔定律 (Biot-Savart’s Law)，估计的Dst指数表示为地心太阳磁层坐标系 (Geocentric Solar Magnetospheric coordinate system, GSM) 中心处磁场扰动的 z 分量：

其中 R 是电流密度 j 的空间位置，ΔV 是网格体积。来自所有个体的扰动贡献在所有网格体积上求和，并累积为Dst指数Dst_{MHD}。该指数的时间分辨率由电流密度 j 决定，而 j 取决于模拟数据输出的任意间隔。

 在本工作中，选择一分钟的分辨率，这与SYM-H指数相同，但远小于标准Dst指数的一小时分辨率。为简便起见，在下文中将继续使用术语 “Dst指数” 来表示模拟的一分钟分辨率Dst指数。

2.2 来自环电流的经验Dst指数 (Empirical Dst Index from Ring Current)

全球MHD模型中缺乏环电流模型将导致Dst指数估计结果不一致。 例如，磁暴期间Dst指数的突然下降无法在模拟中复现，这主要依赖于内磁层 (inner magnetosphere) 环电流的增强。Rae等人 (2010) 证明，在全球模拟中，当行星际磁场 (IMF) 南向期间，内磁层物理在塑造开放与闭合磁力线边界方面起着关键作用。

为了克服这一差异，需要将一个基于物理的、嵌入了环电流的内磁层模型集成到现有的全球磁层MHD模型中 (De Zeeuw, 2004)。这里我们尝试一种不同的方法——使用一个经验模型 (empirical model)。

Burton等人 (1975) 提出了一种仅从太阳风速度、密度和IMF (行星际磁场) 条件知识计算Dst指数的算法。他们的Dst指数方程（方程中为 Dst*）表示为：

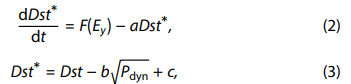
其中：

• a = 3.6 × 10⁻⁵ s⁻¹，是与环电流粒子衰减时间相关的系数；

• P_dyn 代表太阳风的动压 (dynamic pressure)；

• b = 0.2 nT/(eV/cm³)¹ᐟ² 和 c = 20 nT 是系数，分别衡量Dst对太阳风动压和宁静期环电流的响应。

• F(E_y) 代表环电流注入率，它是一个经过延迟和滤波的太阳风电场 E_y 的函数，设定为：

• 

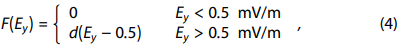
其中 d = -1.5 × 10⁻³ (nT·m)/(mV·s) 是一个常数，用于衡量注入率对 E_y 的响应程度，假设这种响应是线性的。

• F(E_y) 的物理意义是代表粒子注入环电流的速率，它是环电流被晨昏方向太阳风电场增强的速率的函数。

在全球MHD模型中，太阳风电场的y分量 E_y 直接从未受扰动的太阳风速度 v 和 GSM坐标系 中 x = 0 平面处的磁场 B 计算得出：

一旦获得 E_y 和相应的注入率 F，方程 (2) 和 (3) 便被离散化，以在时间上获得经验Dst指数（方程中为 Dst_E）：

注意： 全球磁层电流密度对Dst指数的影响已在全球MHD模型中模拟，可能只考虑来自环电流的贡献，因此通过设定 b = 0 来忽略太阳风动压分量。最终，得到以下方程：

通过这种方式，依赖环电流的Dst指数已通过上述数值实现计算出来，并添加到来自MHD模型的Dst指数中作为最终结果：

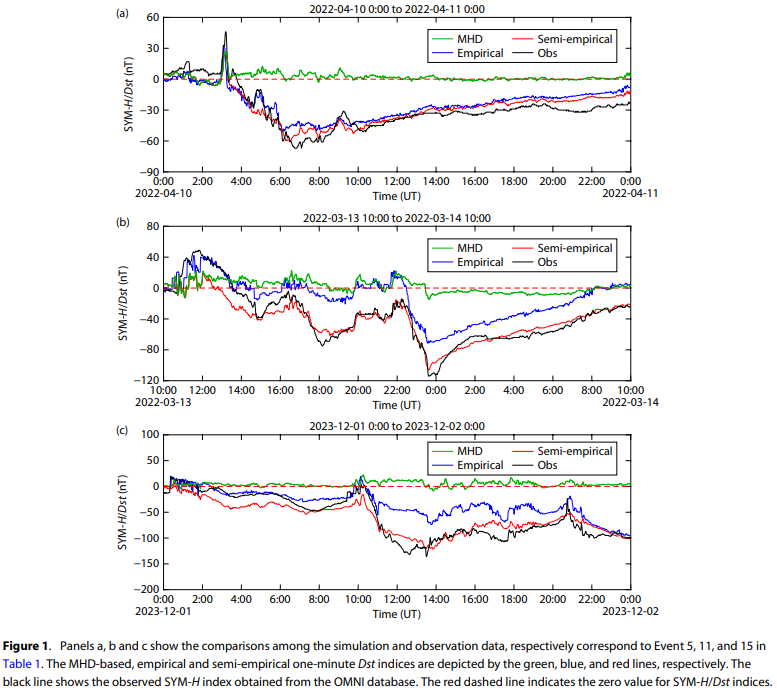
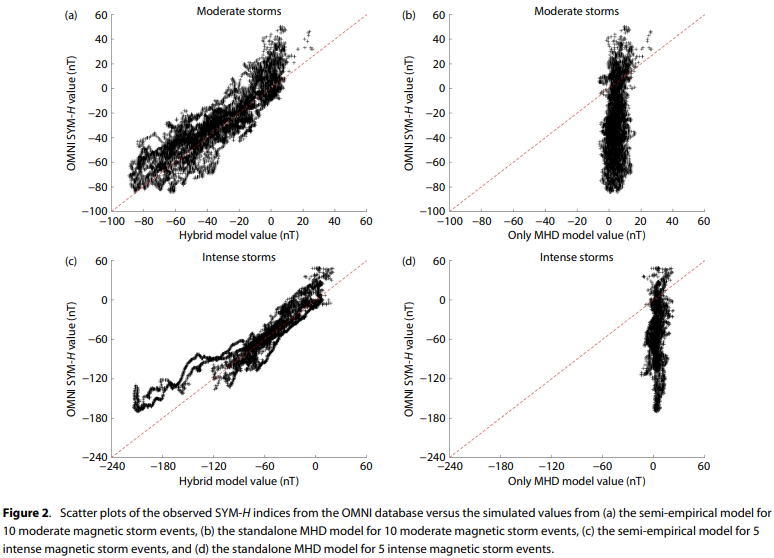
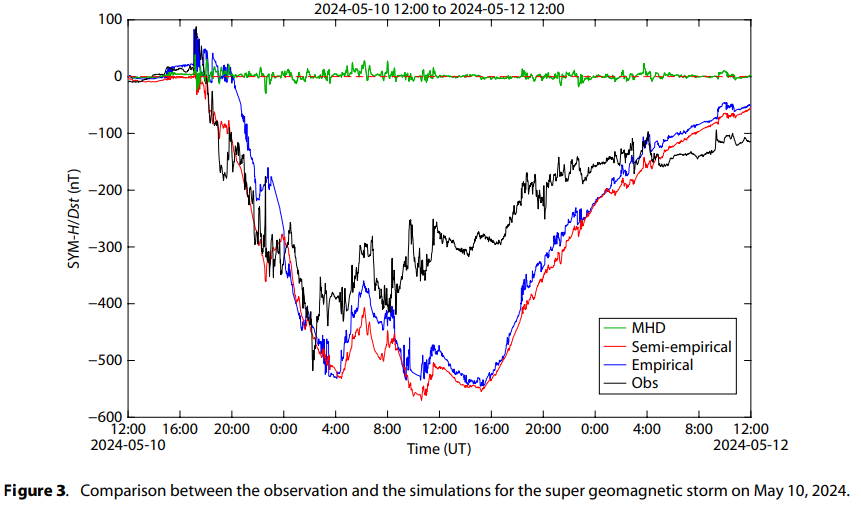
注意：经验分量 Dst_E 不会产生正值，也不能准确预测地磁暴爆发期间Dst指数的突然开始 (sudden commencement)。 然而，MHD分量 Dst_{MHD} 可以有效地模拟由太阳风动压变化引起的Dst变化。 因此，这种半经验模型 (semi-empirical model) 结合了来自基于MHD的磁层电流的Dst贡献和来自经验环电流的Dst贡献，有望在地磁暴期间增强整体模拟性能。模型与观测相比的详细性能将在后续内容中展示。