
笔记整理:兰雅榕,浙江大学硕士生,研究方向为知识图谱、大语言模型
论文链接:https://ojs.aaai.org/index.php/AAAI/article/view/33662
发表会议:AAAI 2025
1. 动机
提高开源大型语言模型(LLM)的数学推理能力是一项有价值但持续的挑战,目前有的利用涉及思维链(CoT) 原理的注释或生成的问题-解决方案数据对对模型进行微调的方法虽然有一定作用,但是对于复杂的数学问题提升不大,且其完全忽略了结合问题思考相应定理的显性思维过程,增加了涉及无关定理和幻觉的危险,该限制阻碍了推理过程的透明度和可解释性,使错误诊断和纠正更加困难。
对于人类而言,能否根据给定的问题选择合适的定理是影响最终解决方案质量的关键因素,但这在 LLM 推理领域的先前研究中却被忽视了。本文提出了一种新颖的方法,以增强 LLM 将数学定理应用于具体问题的能力,我们称之为定理原理 (TR)。
2. 贡献
(1)本文提出了一种方法,用于明确学习如何将定理应用于具体问题,并收集包含 TR 原则的数据集。
(2)本文设计了策略,从问题-定理对中自动演化出面向定理的指令,从而有助于从多个层次的视角学习 TR。
(3)在本文提到的的数据集上进行微调的模型实现了持续的改进,展现了该方法在提升 LLM 数学推理能力方面的潜力。
3. 方法
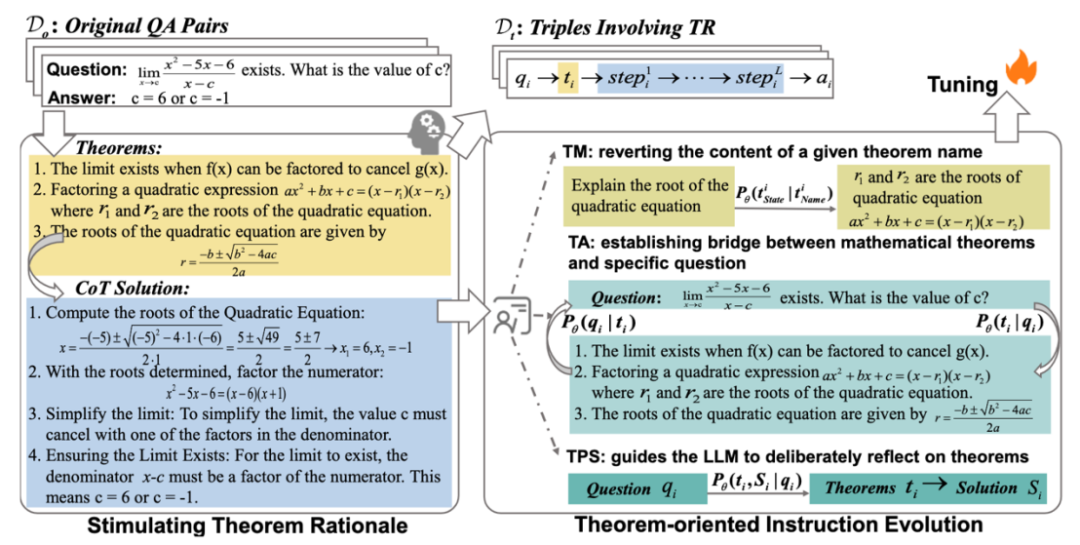
所谓定理基本原理就是涉及为特定问题选择和利用定理原则的联合分布定义,一个关键点在于将特定定理集和特定问题结合的过程,极具挑战但是通常都被忽视。论文中引入了一个特定的提示来刺激 LLM 从每个原始 (qi, ai) 对中自动扩展涉及 TR 的 (qi, ti, Si) 三元组,并伴随着启发式算法进行进一步筛选,以确保数据质量。
原始数据收集:
收集问题-答案对:为LLM提供一些相关信息以生成更准确的三元组,使用BM25从以前的观测中检索最相关的三元组。首先在不同数据集中收集问题-答案对,更关注高水平问题,这些问题对于建立问题和定理之间的联系更有帮助。
生成定理数据:论文中编译了一个专门的提示和少量的上下文示例,以指导 GPT-4o1 从其参数知识中反思对应于 qi 的定理 ti,并在编写解决方案之前明确列出 ti。通过提示中的刺激,生成的响应明确涉及推导出答案 ai 所需的数学定理 ti 和 ti 约束内的逐步解决方案,模仿了人类数学问题解决的过程。因此,我们将 Do 扩展到由并联 (qi, ti, Si) 三元组组成的 Dt。
人工注释和过滤:手动过滤三类不合理样本(包含不一致最终答案的样本,包含明显定理不一致或者错误的样本和包含过长、无意义且重复的解决方案的样本)。此外实施重复数据删除和基于长度的启发式后处理策略。计算 Dt 中所有 (qi, ti, Si) 三元组的解 Si 的长度分布,去除长度异常的解(基于信念:如果模型有足够的信心来掌握问题,则解决方案将在有限的推理步骤内完成。)
以定理为中心的指令优化:
参考人类教师在数学教学化中采用的方法,发展以定理为中心的分层指令;a) 建立概念理解,(b) 将数学概念与其应用联系起来,(c) 培养解决问题的能力。设计与这三种能力对应的指导策略,以从Dt进化指令:
Theorem Memorization(TM)策略:涉及从定理名字到定理内容的映射,从Dt中提取1800个定理完成。
Theorem Alignment (TA):双向TA指令策略:正向出发:提示列出指定问题所需的定理;反向出发:自动编写示例来演示指定定理的应用。
Theorem-based Problem Solving (TPS):模型需要将明确地将思考相应的定理作为解决问题的第一步,而不是像 CoT 中的实践那样将它们耦合到解决方案中。
以 TM、TA 和 TPS 为指导原则,利用 GPT 生成多样化的指令描述,从而从 Dt 中提取总共 30k 的指令数据用于后续训练。
指令微调:
收集了48k个指令和响应数据对,使用因果语言建模来全参数微调llama3-8b。
4. 实验
实验设定:
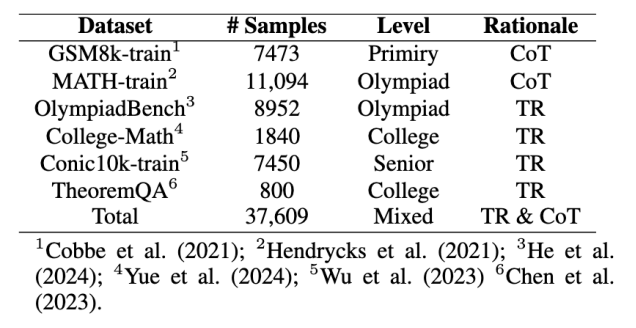
数据集:ID(Conic10K、MATH、GSM8k);OOD(MMLU-pro-Math、JEEBench-Math、SciBench、SAT-Math)包含开放式问题和多项选择题
baseline:具有相同参数尺度的高级开源模型,包括 LLaMA2、Calactica、AQuA-SFT、WizardMath和 MAmmoTHCoT。以及具有代表性的闭源大模型例如 GPT-4、GPT-3.5 和 Claude-2。
评估指标:准确性
实验结果:
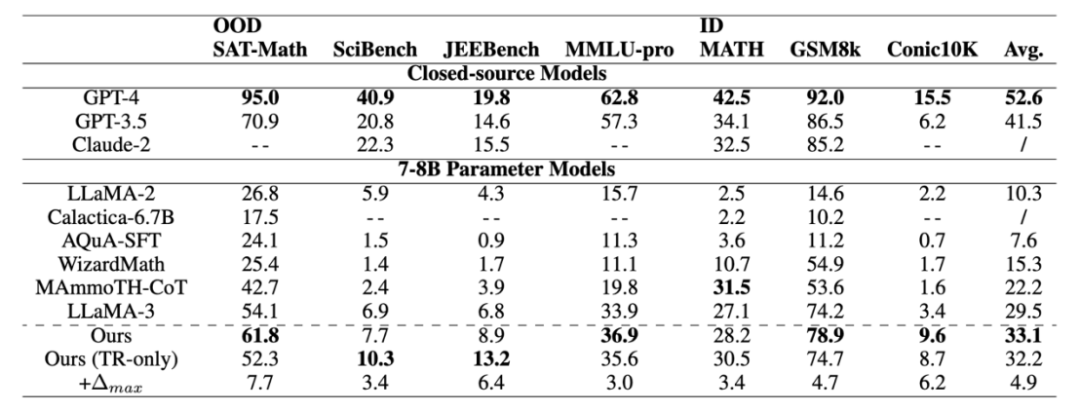
在包含不同数学级别的各种评估数据集中表现出准确性的一致提高,与 IND 数据集相比,模型在 OOD 数据集上获得了更高的性能,这表明从 TR 中学习赋予了模型强大的数学推理能力。
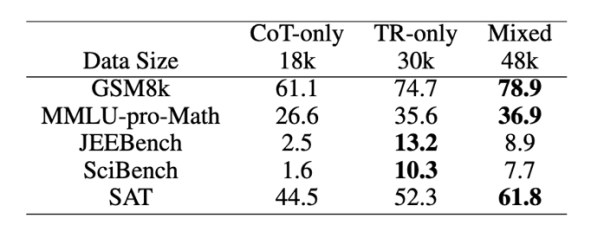
对于知识密集型数学任务,显式学习和利用定理对提高推理能力起着至关重要的作用。
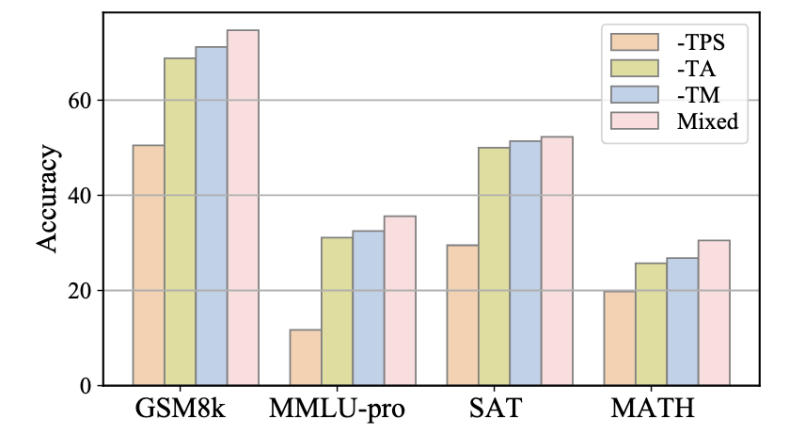
实验还评估了三种指令有效性:对各种提出的面向定理的教学进化策略进行了进一步的消融研究,分别消除了专注于 TM、TA 和 TPS 策略的指令,并使用得到的子集 D-TM、D-TA 和 D-TPS 来微调模型。与使用合并数据集相比,删除这些子集中的任何一个都会导致准确性降低,这凸显了论文提出的指令进化方法而不是直接使用原始问答三元组训练的必要性。比较去除不同子集带来的性能下降,观察到省略 TPS 导致的性能下降最大,其次是 TA 和删除 TM 带来的影响最小。这一发现验证了假设:仅仅将数学定理作为普通文本记忆是远远不够解决数学问题的,关键过程是学习如何将定理应用于特定问题。TA 暗示了将相应的定理与问题对齐的基本原理,而 TPS 在解决方案中进一步引入了定理的约束,因此为解决问题做出了更大的贡献。
5. 总结
本文旨在学习将数学定理应用于具体问题,以提升大型语言模型(LLM)的数学推理能力。该工作精心构建了一个包含并行问题-定理-解三元组的高质量数据集,该数据集涉及TR原则。此外,他们提出了一种以定理为导向的策略来增强三元组中的指令,旨在使LLM能够从不同角度运用定理。在广泛使用的评估基准上进行的大量实验表明,使用此数据集调整的模型获得了强大的数学能力。此外,我们证实了明确引入与定理相关的思想对于提升闭源LLM性能的有效性。该工作为未来的数学推理和纠错工作提供了新的视角。
OpenKG
OpenKG(中文开放知识图谱)旨在推动以中文为核心的知识图谱数据的开放、互联及众包,并促进知识图谱算法、工具及平台的开源开放。







点击阅读原文,进入 OpenKG 网站。

)





:nvidia与cuda介绍)
)

)








