目录
摘要
Abstract
1 CNN--卷积神经网络简介
2 CNN核心操作
2.1 卷积
2.2 池化
3 总结
摘要
本周主要学习了卷积神经网络(CNN)的相关知识,包括概念、基本架构与应用领域等知识,了解了CNN利用其结构高效地从图像等网格化数据中自动提取多层次特征的方法,重点学习了卷积与池化两大核心操作,认识了卷积背后的设计思想,理解了卷积核的使用与计算过程,同时还掌握了池化操作的类型(如最大池化、平均池化)、功能及计算方法。
Abstract
This week, I primarily studied the concepts, basic architecture, and application fields of Convolutional Neural Networks (CNNs). I gained an understanding of how CNNs leverage their specialized structure to efficiently extract hierarchical features from grid-like data such as images. Particular emphasis was placed on the two core operations—convolution and pooling. I explored the underlying design principles of convolution and acquired knowledge of convolutional kernels, their application, and the associated computational process. Additionally, I studied the types of pooling operations (e.g., max pooling and average pooling), their functional roles, and the mechanics of their computation.
1 CNN--卷积神经网络简介
卷积神经网络(Convolutional Neural Network, 简称 CNN)是在传统神经网络(特别是全连接前馈神经网络,也称多层感知机(MLP))的基础上发展出来的一种专门用于处理网格结构数据的深度学习模型,尤其是二维图像数据,因此在图像识别和处理领域表现出色。其设计灵感来源于生物视觉皮层中神经元的感受野机制,能够自动并高效地从原始数据中提取空间层级特征。
全连接前馈神经网络的结构就如之前所学的,包括一个输入层,一个输出层与数个隐藏层,如下图所示。全连接代表相邻两层的每个神经元都与另一层的所有神经元相连接;前馈代表信息从输入层开始,逐层向前传递,最终到达输出层;而多层感知机中的多层则代表包含一个或多个隐藏层,与无隐藏层的单层感知机相区别。
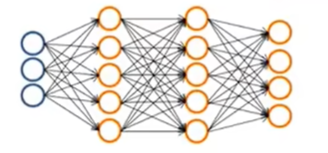
在使用这种结构处理图像时,可能会出现下列问题:
1.参数爆炸问题。例如,假设输入是一张 1000×1000 的图像,则输入维度为 1000000。如果第一隐藏层有 1000 个神经元,则仅这一层就需要 个参数。这会导致模型计算复杂度过高,难以训练且容易过拟合。
2.忽略空间局部性。这种结构将每个像素视为独立特征,忽略了图像中像素之间的空间邻近关系和局部模式(如边缘、纹理),无法有效捕捉局部特征。
3.缺乏平移不变性。如果图像中的物体发生平移,这种结构会将其视为完全不同的输入,导致识别失败。
为了解决上述问题,卷积神经网络引入了卷积和池化两个操作,也由此,一个完整的卷积神经网络通常包括输入层、卷积层 、激活函数层、池化层 、展平层、全连接层与输出层,有时也会有归一化层。卷积层使用可学习的卷积核在输入数据上滑动以提取局部特征;激活函数层通常位于线性变换(如全连接层、卷积层)之后,引入非线性,使网络能拟合复杂函数,常用 ReLU函数(计算高效);池化层降低特征图的空间尺寸(下采样),减少计算量,一定程度上增强平移不变性;展平层在全连接层前,将多维特征图展平为一维向量,为全连接层做准备,有的说法会合并到全连接层;全连接层通常位于网络末端,将高层特征整合,输出一维信息,用于最终分类或回归,其后可以添加全连接层,但不能再加卷积层与池化层,如果要以图像的形式输出,可以将全连接层去掉;归一化层对小批量数据进行标准化,加速训练,提升稳定性。
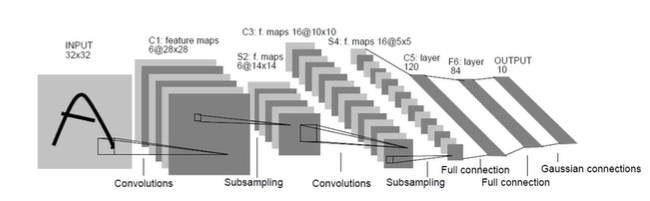
卷积神经网络的主要应用领域是计算机视觉,包括图像分类检索、目标检测与人脸识别等。例如在医疗影像分析时可用于X光、CT、MRI等医学图像的病灶检测(如肺结节、肿瘤)、分割与诊断辅助,具有重要的临床价值。另外它也可用于自然语言处理(NLP),进行文本分类、情感分析与句子建模等任务。
2 CNN核心操作
2.1 卷积
卷积操作背后的设计思想和机制是局部连接与权值共享。
对于图像而言,它具有非常强的区域性,其中的一个像素点,可能只与离它近的像素点关系大,而与离它远的关系小。例如,对于一张人脸照,其眼部的一个像素点与其周围的关系比较大,而与头发部分的关系较小。如果采用局部连接的方式,使每个神经元只与输入图像的一个局部区域连接,就可以在大幅减少参数数量的同时保留对局部空间结构的建模能力,这个局部区域也被称为感受野(Receptive Field)。
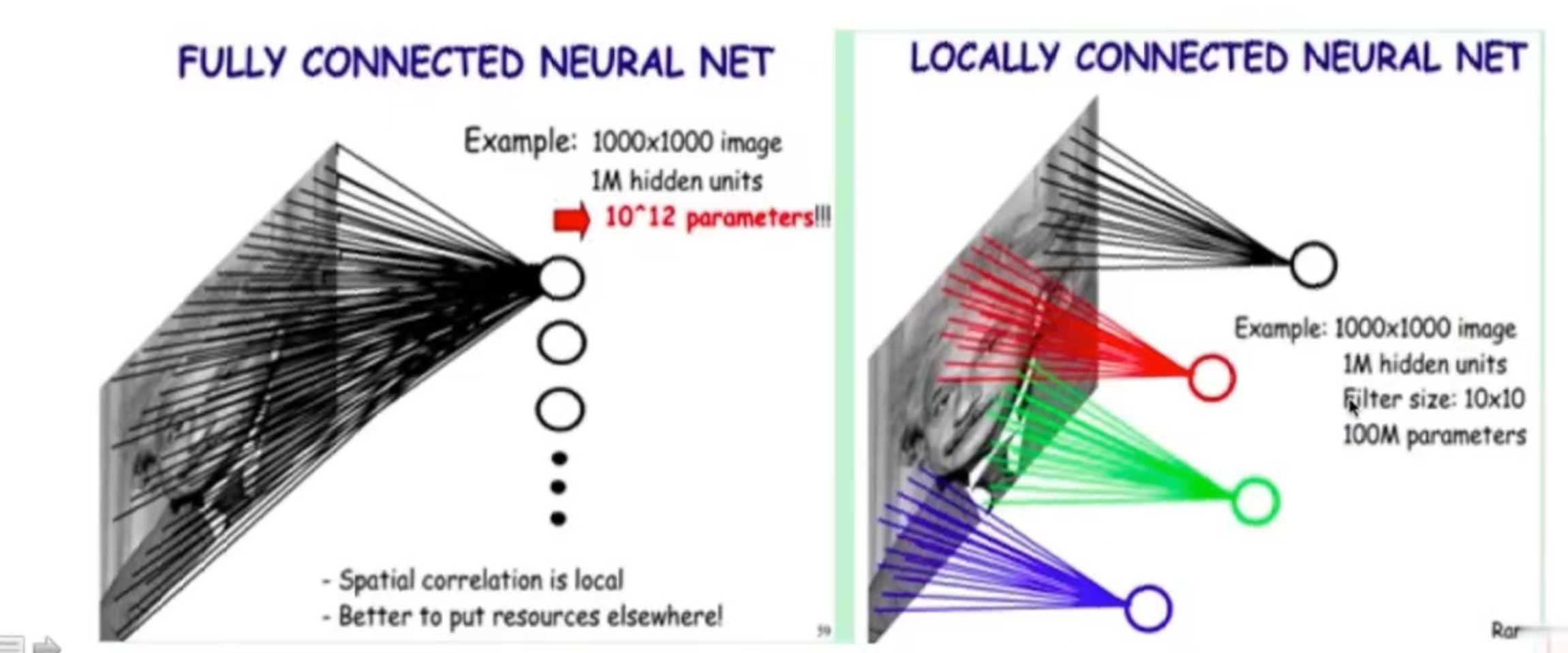
除此之外,图像中的某个特征与其在图像中的位置是无关的。比如对于同样一张人脸,由于拍摄角度的问题,一张照片的眼睛在左边,而另一张的在右边。如果用同一个神经元提取相同位置的特征,由于特征位置在变化,神经元提取到的特征也在变化,那么就不好进行学习。如果采用权值共享的方式,使一组固定的权重在整个输入图像上滑动并重复使用,就可以在继续减少参数数量的基础上实现了平移不变性,这组固定的权重就被称为卷积核。
卷积核(也称为滤波器,Filter)是卷积神经网络中最核心的可学习组件,负责从输入数据(如图像)中提取局部特征。它一般是一个小的数值矩阵,通过与输入数据的局部区域进行点积运算(即卷积操作),生成一个特征图,特征图尺寸公式如下:
其中 W 是输入尺寸,K 是卷积核大小。
即,若输入图像大小为 ,卷积核大小为
,那么输出的特征图尺寸应为
。
下面是一个卷积计算的例子:

的值由蓝框部分与卷积核进行内积运算得到,
的值由蓝框部分向右移一位与卷积核进行内积运算得到,
的值由蓝框部分向下移一位与卷积核进行内积运算得到,其他依此类推。
每次计算,蓝色框都会向右或向下进行移动,移动的距离就是卷积中另一个参数,步长(stride),它控制着卷积核在图像上滑动时每次移动的像素距离。步长越大,卷积核扫描的次数越少,输出特征图的尺寸就越小。引入该参数后,输出特征图尺寸公式如下:
其中 S 就代表步长大小。
前面的例子假设步长为1。如果假设步长为2,那么就会变成:

另外,可以观察到,输出特征图相对输入图像的尺寸是减小的,为了使两者尺寸一致,可以在输入图像的周围加上一些默认值0,即进行填充(padding),填充尺寸公式如下:
同时,如果加入填充,输出特征图尺寸公式如下(有时可能需要别的尺寸):
因此,为了能够对称填充,即在输入图像的上下和左右都进行填充,通常要求卷积核大小为奇数。
前面的计算都是单通道的,如果要处理多通道数据,可以将卷积核也变为多通道,并将之与每个通道相对应的输入数据做内积运算,从而得到输出,每个通道上的参数相互独立。
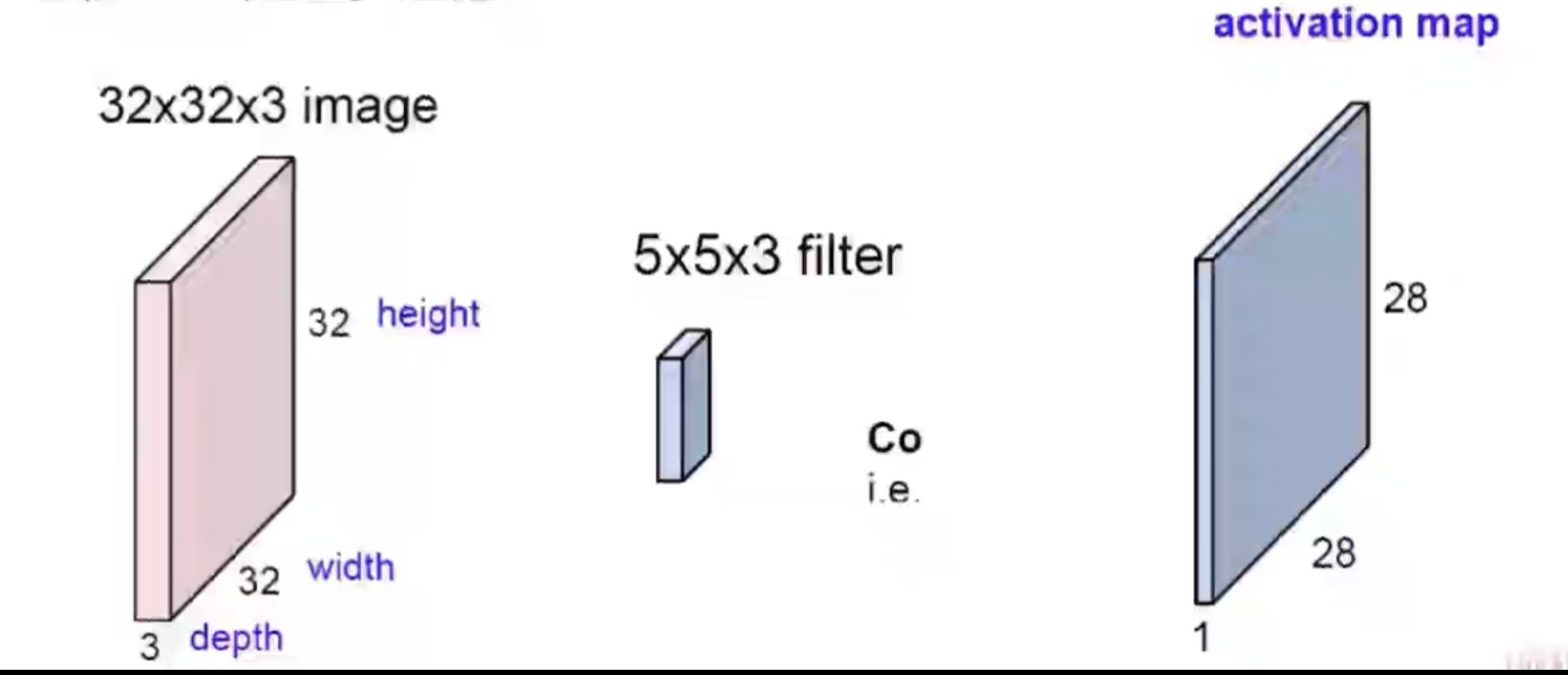
这种情况下,每个卷积核只生成一个输出特征图,如果要得到多通道输出特征图,可以采用多个卷积核,此时卷积核数即为最后生成的特征图的通道数。CNN中真正使用的就是多个多通道的卷积核结构,故卷积核参数量的计算公式为:
Ci 与 Co 分别为输入与输出的通道数,Kw 和 Kh 分别为卷积核长宽。
2.2 池化
池化层采取的池化操作主要利用池化核进行,包括最大池化与平均池化。前者取池化核覆盖输入数据区域的最大值作为输出,保留最显著的特征,最常用;后者取池化核覆盖输入数据区域的平均值作为输出,平滑特征,常用于全连接层前的全局平均池化。池化默认步长与池化核尺寸一致,无重叠。且通常不进行填充,如果有多的则忽略(比如输入为 ,而池化核只有
)。
举例如下:
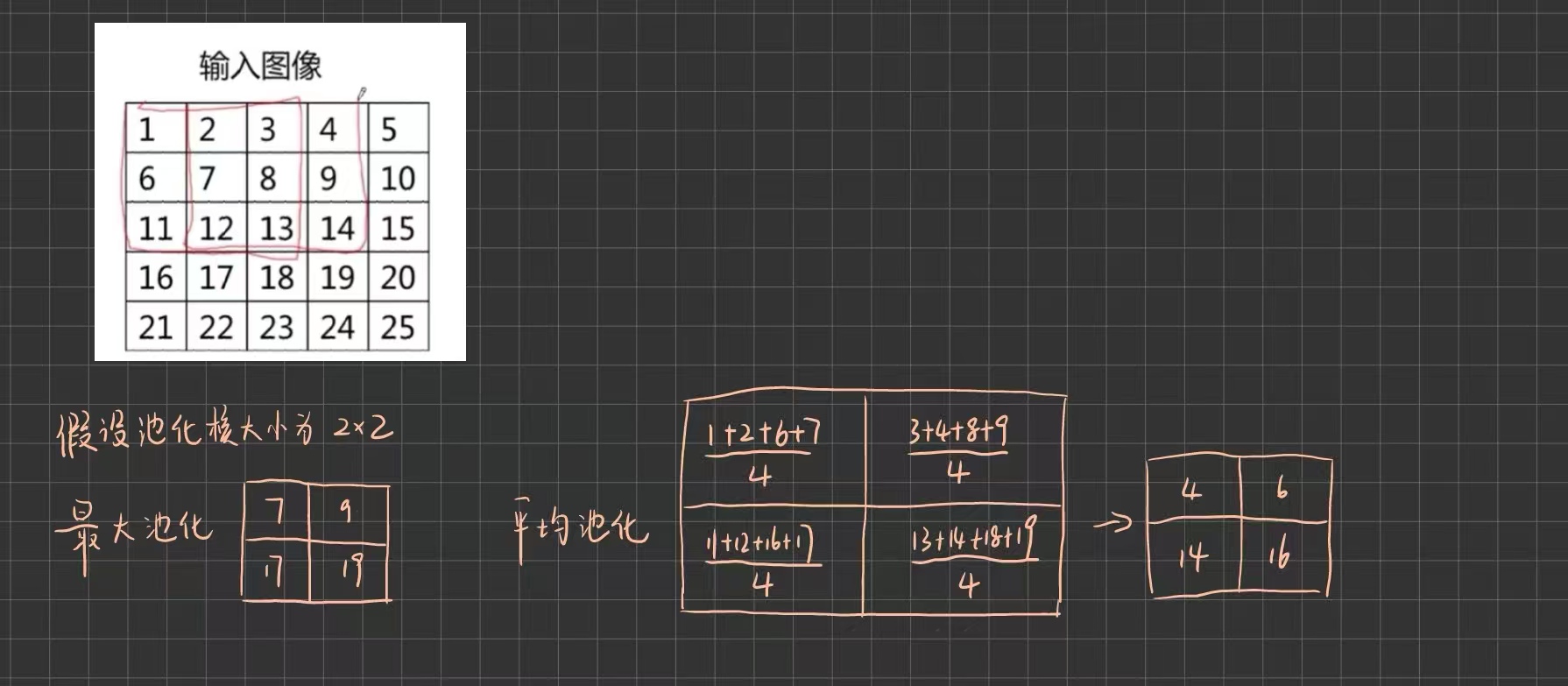
池化操作是固定的数学运算,没有可学习的参数,因此不参与反向传播中的梯度更新。它可以减少图像尺寸,从而使计算量减少,能够一定程度减少平移鲁棒,即使有小幅度偏移,池化结果可能也一样,但这样会损失空间位置精度。
3 总结
本周主要学习了卷积神经网络的相关知识,重点了解了卷积和池化两大操作及其计算。下周计划学习卷积神经网络的经典网络架构,并进行代码实战,加深对其的理解。




常用命令全解析:从基础到进阶)







——线性表(顺序存储和链式存储))
)

微服务篇-参考回答)



(日更))