一、已知无向图的邻接矩阵，求无向图的邻接表。
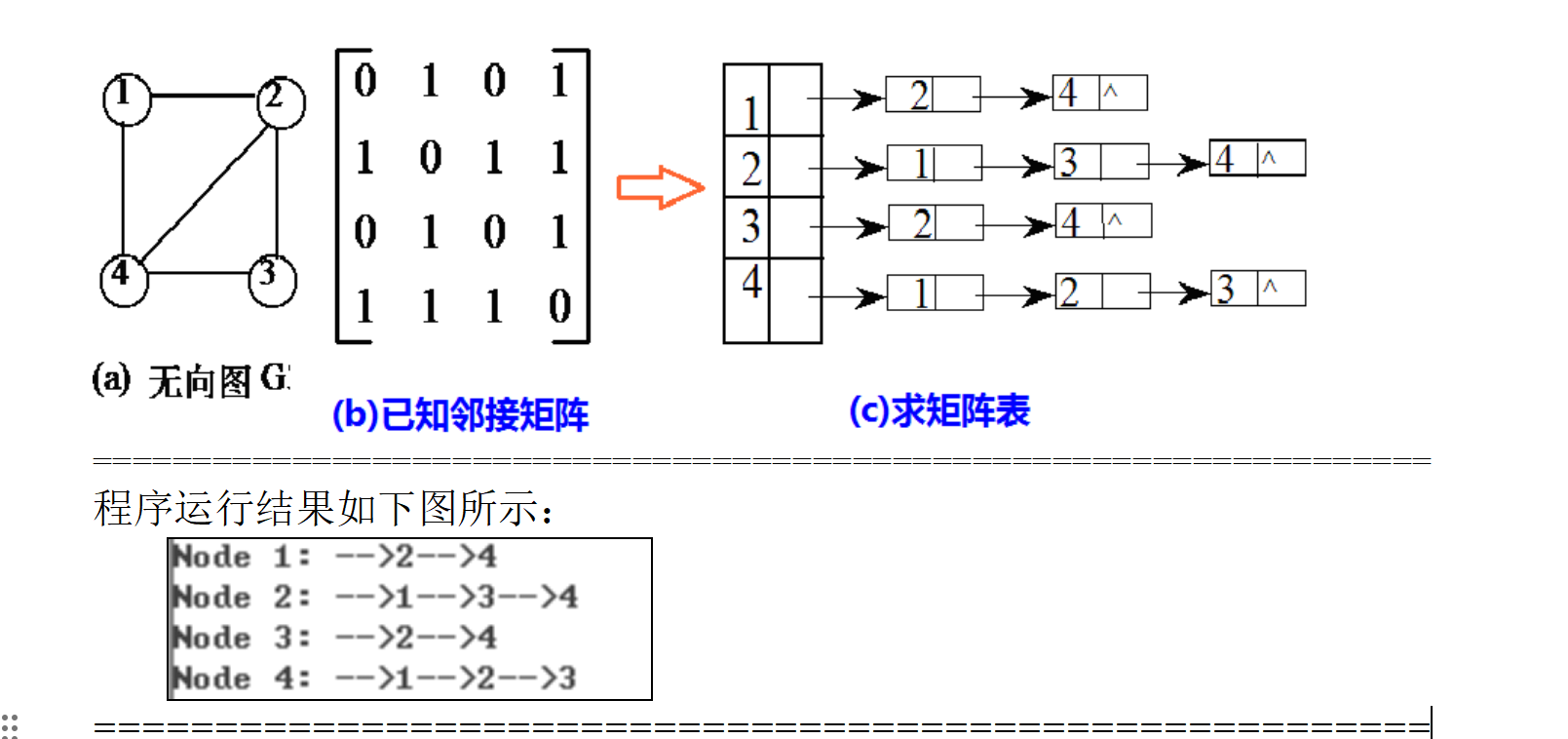
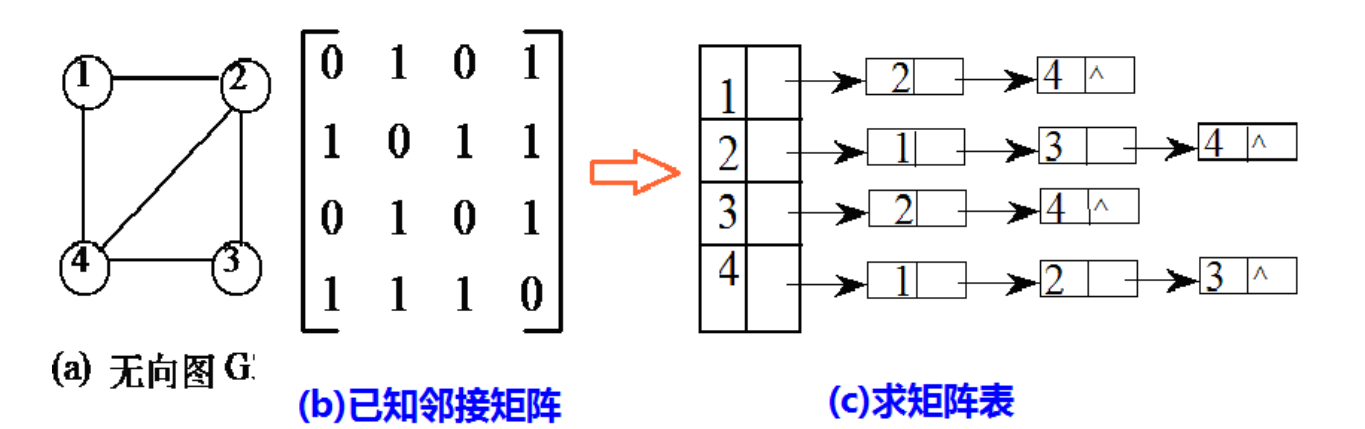
（1）提示：无向图如下图(a)所示，已知邻接矩阵如图(b)所示，求对应的邻接表(c)。
（2）请定义void adjMatrix_2_adjList(int b[4][4], AdjList a)函数。
typedef struct LNode
{int data;//顶点信息，代表入度顶点struct LNode *next;
}LNode, *LinkList;typedef struct
{int data; //顶点信息，代表出度顶点LinkList head;
}AdjList[4];//共4个顶点void adjMatrix_2_adjList(int b[4][4], AdjList a)
{ LNode=*p, *G;
for(int i = 0; i <=4; i++){a[i].head = NULL;a[i].data=i+1;}
for(int i = 1; i <= 4; i++){a.vertives[i].head = NULL;}
for(int i=0;i<=4;i++)
{ for(int j=0;j<=4;j++)
{if(b[i][j]==1)
{p=(LNode*)mallo(sizelof(LNode));
p->data=j+1;p->next= NULL;
if(!a[i].head)a[i].head=p;
else{G=a[i].head;}
while{G->next}
G=G->next;
G->next=p;
}
}
}
}void print_AdjList(AdjList a)//打印邻接表
{for(int i=0; i<4; i++){printf("Node %d: ", a[i].data);LNode *p = a[i].head;while(p != NULL){printf("-->%d", p->data);p = p->next;}printf("\n");}
}二、实现如下功能：已知无向图的邻接表，判断该邻接表是否连通。
//1. 提示：函数可以写成如下形式BOOL judge_is_connected(adjList b[ ])
//2. 提示：（a）结构体自己定义；（b）定义提示1的函数
void BOOL judge_is_connected(adjList b[ ])
{
for(int i= 1,i<=4;i++)
{G->book[i]=0；}
DFS(*a，0);
for(int i= 1,i<=4;i++)
{
if(!G->book[i])
{
return 0;
}
}
return 1;
}
}三、已知无向图的邻接矩阵，求该邻接矩阵的深度优先遍历 。
（1）提示：无向图如下图(a)所示，其邻接矩阵如图(b)所示。
（2）请定义void DFS(MGraph *G, int ves)函数。
#include<stdio.h>
#define MAX 100
#define NUM 8 //图的顶点个数typedef struct
{int e[MAX][MAX];int vesNum; //图中的顶点数；int book[MAX];//标志判断是否有被访问过
}MGraph;int a[NUM][NUM] = { 0, 1, 1, 0, 0, 0, 0, 0,1, 0, 0, 1, 1, 0, 0, 0,1, 0, 0, 0, 0, 1, 1, 0,0, 1, 0, 0, 0, 0, 0, 1,0, 1, 0, 0, 0, 0, 0, 1,0, 0, 1, 0, 0, 0, 0, 1,0, 0, 1, 0, 0, 0, 0, 1,0, 0, 0, 1, 1, 1, 1, 0 };void createMGraph(MGraph *G)
{int i, k;G->vesNum = NUM;//没被访问过的结点置为0for(i=0; i<G->vesNum; i++) G->book[i]=0;//创建邻接矩阵for(i=0; i<G->vesNum; i++)for(k=0; k<G->vesNum; k++)G->e[i][k] = a[i][k];
}
void DFS(MGraph *G,int ves)
{G->book[ves] =1;
printf(“%d”,ves);
for(int i=0;i<G.vesNum;i++)
{if(!G->book[ves])&&(G->e[ves][i]!= MAX)}
{DFS(G,i)}
}
}
void main()
{MGraph G;createMGraph(&G);DFS(&G, 0); //0表示从第1个点开始搜索，如果是1表示从第2个点开始：）
}
)
