目录

一、算法复杂度

二、时间复杂度

1.不同时间度代码举例

三、空间复杂度

一、算法复杂度

        算法复杂度（评估算法优劣一个重要指标）分为时间复杂度和空间复杂度。
        时间复杂度是指执行算法所需要的计算工作量，而空间复杂度是指执行这个算法所需要的内存空间。
        算法的复杂性体运行该算法时的计算机所需资源的多少上，计算机资源最重要的是时间和空间（即寄存器）资源，因此复杂度分为时间和空间复杂度。

二、时间复杂度

        一个算法所需的运算时间通常与所解决问题的规模大小有关，即与算法中语句的执行次数成正比例，哪个算法中语句执行次数多，它花费时间就多。一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)。

常见的算法时间复杂度由小到大依次为：
Ο(1)＜Ο(log 2n)＜Ο(n)＜Ο(n log⁡2n)＜Ο(n^2)＜Ο(n^3) ＜ Ο(2^n) ＜ Ο(n!)

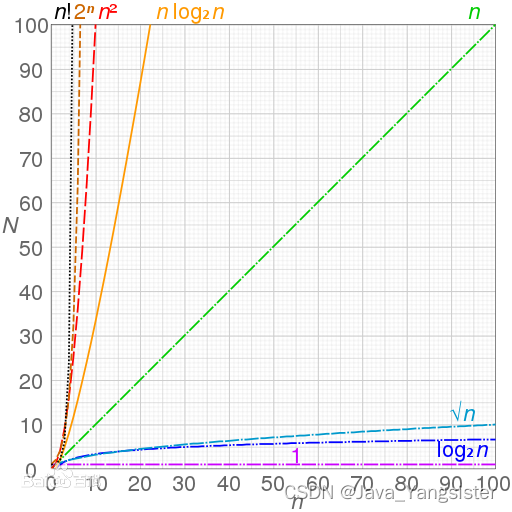
1.不同时间度代码举例

#include <stdio.h>// O(1) 常数时间 - 访问数组元素
int access_element(int arr[], int size) {return arr[0];
}// O(log n) 对数时间 - 二分查找
int binary_search(int arr[], int left, int right, int target) {while (left <= right) {int mid = left + (right - left) / 2;if (arr[mid] == target)return mid;if (arr[mid] < target)left = mid + 1;elseright = mid - 1;}return -1;
}// O(n) 线性时间 - 遍历数组
void traverse_array(int arr[], int size) {for (int i = 0; i < size; i++) {printf("%d ", arr[i]);}printf("\n");
}// O(n log n) 线性对数时间 - 归并排序
void merge(int arr[], int left, int mid, int right) {int n1 = mid - left + 1;int n2 = right - mid;int L[n1], R[n2];for (int i = 0; i < n1; i++)L[i] = arr[left + i];for (int j = 0; j < n2; j++)R[j] = arr[mid + 1 + j];int i = 0, j = 0, k = left;while (i < n1 && j < n2) {if (L[i] <= R[j]) {arr[k] = L[i];i++;} else {arr[k] = R[j];j++;}k++;}while (i < n1) {arr[k] = L[i];i++;k++;}while (j < n2) {arr[k] = R[j];j++;k++;}
}void merge_sort(int arr[], int left, int right) {if (left < right) {int mid = left + (right - left) / 2;merge_sort(arr, left, mid);merge_sort(arr, mid + 1, right);merge(arr, left, mid, right);}
}// O(n²) 平方时间 - 冒泡排序
void bubble_sort(int arr[], int size) {for (int i = 0; i < size - 1; i++)for (int j = 0; j < size - i - 1; j++)if (arr[j] > arr[j + 1]) {int temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}
}// O(n³) 立方时间 - 矩阵乘法
void matrix_multiply(int a[][10], int b[][10], int result[][10], int n) {for (int i = 0; i < n; i++)for (int j = 0; j < n; j++)for (int k = 0; k < n; k++)result[i][j] += a[i][k] * b[k][j];
}// O(2^n) 指数时间 - 汉诺塔问题
void hanoi(int n, char source, char auxiliary, char target) {if (n > 0) {hanoi(n - 1, source, target, auxiliary);printf("Move disk %d from %c to %c\n", n, source, target);hanoi(n - 1, auxiliary, source, target);}
}// O(n!) 阶乘时间 - 排列 (部分示例)
void permute(int arr[], int start, int end) {if (start == end) {for (int i = 0; i <= end; i++)printf("%d ", arr[i]);printf("\n");return;}for (int i = start; i <= end; i++) {int temp = arr[start];arr[start] = arr[i];arr[i] = temp;permute(arr, start + 1, end);temp = arr[start];arr[start] = arr[i];arr[i] = temp;}
}

三、空间复杂度

一个算法的空间复杂度是指程序运行开始到结束所需要的存储空间。包括算法本身所占用的存储空间、输入/输出占用的存储空间以及算法在运行过程中的工作单元和实现算法所需辅助空间。