封装红黑树实现mysetmymap

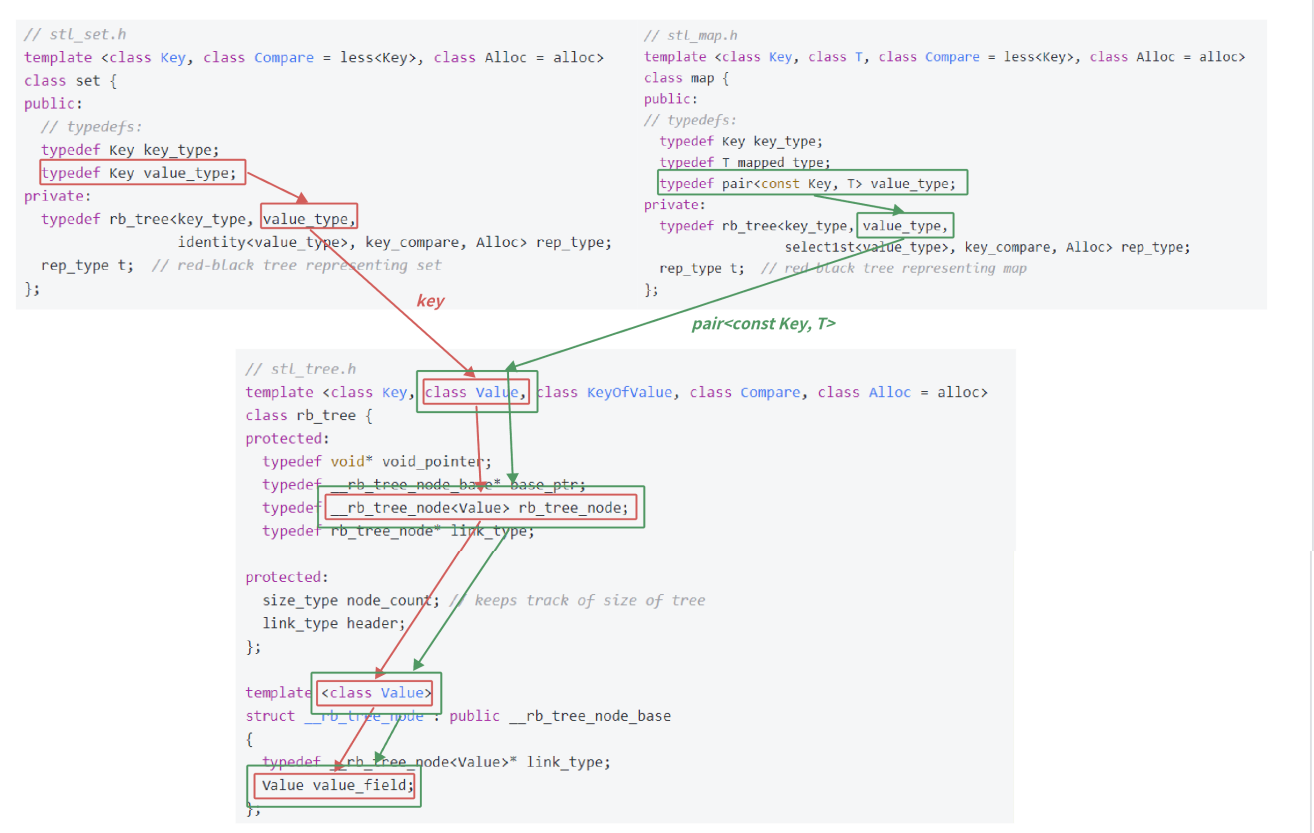
1. 源码分析

  • set实例化rb_tree时第二个模板参数给的是key，map实例化rb_tree时第⼆个模板参数给的是 pair<const key,T>，这样一颗红黑树既可以实现key搜索场景的set，也可以实现key/value搜索场 景的map
  • 源码里面模板参数是用T代表value，而内部写的value_type不是日常 key/value场景中说的value，源码中的value_type反而是红黑树结点中存储的真实的数据的类型
  • 为什么set要传两个key？因为对于 map和set，find/erase时的函数参数都是Key，第一个模板参数是传给find/erase等函数做形参的类型的。对于set两个参数是一样的，对于map不一样了，map的insert是pair对象，但是find和ease的是Key对象

2. 模拟实现map和set

2.1 复用红黑树的框架

  • key参数就用K，value参数就用V，红黑树中的数据类型使用T
  • 因为RBTree实现了泛型不知道T参数导致是K，还是pair<K,V>，那么insert内部进行插入逻辑比较时，就没办法进行比较，因为pair的默认支持的是key和value一起参与比较，我们需要时的任何时候只比较key，所以在map和set层分别实现一个MapKeyOfT和SetKeyOfT的仿函数传给RBTree的KeyOfT，然后RBTree中通过KeyOfT仿函数取出T类型对象中的key，再进行比较
//myset.h
namespace smc{template <class K>
class set
{struct SetKeyOfT {const K& operator()(const K& key){return key;}};
public:
private:RBTree<K,const K, SetKeyOfT> _rbtree;
};}
//mymap.h
namespace smc
{template<class K,class V>class map {struct MapKeyOfT{ const K& operator()(const pair<K, V>& kv){return kv.first;}};public:private:RBTree<K, pair<const K, V>, MapKeyOfT> _rbtree;};
}
// RBTree.h// 实现步骤： 
// 1、实现红黑树 
// 2、封装map和set框架，解决KeyOfT 
// 3、iterator 
// 4、const_iterator 
// 5、key不支持修改的问题 
// 6、operator[] 
enum Colour
{RED,BLACK
};
template<class T>
struct RBTreeNode
{T _data;RBTreeNode<T>* _left;RBTreeNode<T>* _right;RBTreeNode<T>* _parent;Colour _col;RBTreeNode(const T& data): _data(data), _left(nullptr), _right(nullptr), _parent(nullptr){}
};
template<class K, class T, class KeyOfT>
class RBTree
{
private:typedef RBTreeNode<T> Node;Node* _root = nullptr;public:bool Insert(const T& data){if (_root == nullptr){_root = new Node(data);_root->_col = BLACK;return true;}KeyOfT kot;Node* parent = nullptr;Node* cur = _root;while (cur){if (kot(cur->_data) < kot(data)){parent = cur;cur = cur->_right;}else if (kot(cur->_data) > kot(data)){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(data);Node* newnode = cur;// 新增结点。颜⾊给红⾊ cur->_col = RED;if (kot(parent->_data) < kot(data)){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;//...return true;}
}

2.2 支持iterator的实现

  • terator实现的框架跟list的iterator思路是一致的，用个类型封装结点的指针，再通过重载运算符实现，迭代器像指针一样访问的行为
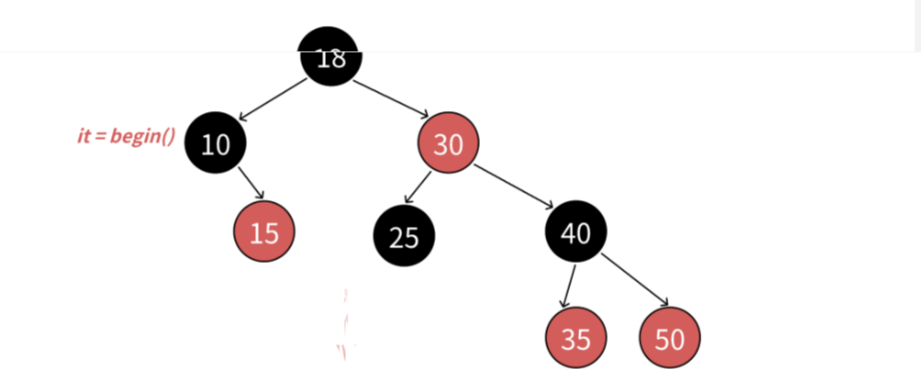
  • 这里的难点是operator++和operator--的实现。之前使⽤部分，map和set的迭代器走的是中序遍历，左子树->根结点->右子树，那么begin()会返回中序第一个结点的iterator也就是10所在结点的迭代器
  • 迭代器++时，如果it指向的结点的右子树不为空，代表当前结点已经访问完了，要访问下一个结点 是右子树的中序第一个，一棵树中序第一个是最左结点，所以直接找右子树的最左结点即可
  • 迭代器++时，如果it指向的结点的右子树为空，代表当前结点已经访问完了且当前结点所在的子树也访问完了，要往上走。而且如果当前it是其父节点的右子树，表示这整个子树都完了，就要去找it的祖先节点
  1. 如果当前结点是父亲的左，根据中序左子树->根结点->右子树，那么下一个访问的结点就是当前结 点的父亲；如下图：it指向25，25右为空，25是30的左，所以下一个访问的结点就是30
  2. 如果当前结点是父亲的右，根据中序左子树->根结点->右子树，当前当前结点所在的子树访问完 了，当前结点所在父亲的子树也访问完了，那么下一个访问的需要继续往根的祖先中去找，直到找 到孩⼦是父亲左的那个祖先就是中序要问题的下一个结点。如下图：it指向15，15右为空，15是10 的右，15所在子树话访问完了，10所在子树也访问完了，继续往上找，10是18的左，那么下一个 访问的结点就是18
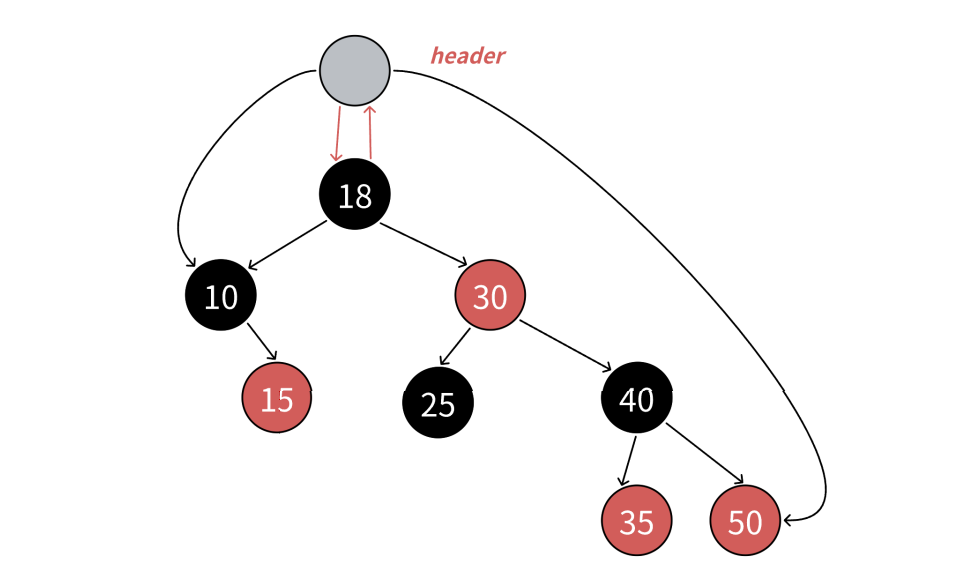
  • end()如何表示？如下图：当it指向50时，++it时，50是40的右，40是30的右，30是18的右，18 到根没有父亲，没有找到孩⼦是父亲左的那个祖先，这是父亲为空了，那我们就把it中的结点指针置为nullptr，用nullptr去充当end。需要注意的是stl源码空，红黑树增加了一个哨兵位头结点 做为end()，这哨兵位头结点和根互为父亲，左指向最左结点，右指向最右结点。相比我们用 nullptr作为end()，只是--end()判断到结点时空，特殊处理一下，让迭代器结点指向最右结点。具体参考迭代器--实现
  • 迭代器--的实现跟++的思路完全类似，逻辑正好反过来即可，访问顺序是右子树->根结点-> 左子树
  • set的iterator也不支持修改，我们把set的第⼆个模板参数改成const K即可， 即RBTree<K,pair<K,V>,SetKeyOfT> _rbtree
  • map的iterator不支持修改key但是可以修改value，我们把map的第二个模板参数pair的第一个参数改成const K即可，即RBTree<K, pair<const K, V>, MapKeyOfT> _rbtree;

2.3 map支持[ ]

map要支持[ ]主要需要修改insert返回值支持，修改RBtree中的insert返回值为

pair<Iterator,bool> Insert(const T& data)

2.4 smc::set和smc::map代码实现

dwaekkiyo/test - Gitee.com

//set.h
namespace smc
{template <class K>class set{struct SetKeyOfT {const K& operator()(const K& key){return key;}};public:typedef typename RBTree<K,const K, SetKeyOfT>::Iterator iterator;typedef typename RBTree<K,const K, SetKeyOfT>::ConstIterator const_iterator;iterator begin(){return _rbtree.begin();}iterator end(){return _rbtree.end();}const_iterator begin() const{return _rbtree.begin();}const_iterator end() const{return _rbtree.end();}pair<iterator,bool> insert(const K& key){return _rbtree.Insert(key);}iterator Find(const K& key){_rbtree.Find(key);}private:RBTree<K,const K, SetKeyOfT> _rbtree;};
}
//map.h
namespace smc
{template<class K,class V>class map {struct MapKeyOfT{ const K& operator()(const pair<K, V>& kv){return kv.first;}};public:typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::Iterator iterator;typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::ConstIterator const_iterator;iterator begin(){return _rbtree.begin();}iterator end(){return _rbtree.end();}const_iterator begin() const{return _rbtree.Begin();}const_iterator end() const{return _rbtree.End();}pair<iterator,bool> insert(const pair<K,V> kv){return _rbtree.Insert(kv);}V& operator[](const K& key){pair<iterator, bool> ret = _rbtree.Insert({ key,V() });return ret.first->second;}iterator Find(const K& key){_rbtree.Find(key);}private:RBTree<K, pair<const K, V>, MapKeyOfT> _rbtree;};void test_map(){map<string, string> dict;dict.insert({ "sort", "排序" });dict.insert({ "left", "左边" });dict.insert({ "right", "右边" });dict["left"] = "左边，剩余";dict["insert"] = "插入";dict["string"];map<string, string>::iterator it = dict.begin();while (it != dict.end()){// 不能修改first，可以修改second //it->first += 'x';it->second += 'x';cout << it->first << ":" << it->second << endl;++it;}cout << endl;}
}
//RBTree.h
#pragma onceenum Colour
{Red,Black
};template <class T>
struct RBTreeNode {T _data;RBTreeNode<T>* _left;RBTreeNode<T>* _right;RBTreeNode<T>* _parent;Colour _col;RBTreeNode(const T& data):_data(data), _left(nullptr), _right(nullptr), _parent(nullptr){}
};template <class T,class Ref,class Ptr>
struct RBTreeIterator
{typedef RBTreeNode<T> Node;typedef RBTreeIterator<T,Ref,Ptr> Self;Node* _node;Node* _root;RBTreeIterator(Node* node,Node* root):_node(node),_root(root){}Self& operator++(){if (_node->_right){Node* minleft = _node->_right;while (minleft->_left){minleft = minleft->_left;}_node = minleft;}else{Node* cur = _node;Node* parent = cur->_parent;while (parent && cur == parent->_right){cur = parent;parent = parent->_parent;}_node = parent;}return *this;}Self& operator--(){if (_node == nullptr){//在end位置Node* rightmost = _root;while (rightmost && rightmost->_right){rightmost = rightmost->_right;}_node = rightmost;}else if (_node->_left){// 左子树不为空，中序左子树最后⼀个 Node* rightmost = _node->_left;while (rightmost->_right){rightmost = rightmost->_right;}_node = rightmost;}else{Node* cur = _node;Node* parent = cur->_parent;while (parent && cur == parent->_left){cur = parent;parent = parent->_parent;}_node = parent;}return *this;}Ref operator*() {return _node->_data;}Ptr operator->(){return &(_node->_data);}bool operator!=(const Self& s){return _node != s._node;}bool operator==(const Self& s){return _node == s._node;}};template<class K, class T,class KeyOfT>
class RBTree
{typedef RBTreeNode<T> Node;public:typedef RBTreeIterator<T,T&,T*> Iterator;typedef RBTreeIterator<T,const T&,const T*> ConstIterator;Iterator begin(){Node* cur = _root;while (cur&& cur->_left){cur = cur->_left;}return Iterator(cur,_root);}Iterator end(){return Iterator(nullptr,_root);}ConstIterator begin() const{Node* cur = _root;while (cur && cur->_left){cur = cur->_left;}return ConstIterator(cur, _root);}ConstIterator end() const{return ConstIterator(nullptr, _root);}pair<Iterator,bool> Insert(const T& data){if (_root == nullptr){_root = new Node(data);_root->_col = Black;return make_pair(Iterator(_root,_root),true);}Node* cur = _root;Node* parent = nullptr;KeyOfT kot;while (cur){if (kot(cur->_data) > kot(data)){parent = cur;cur = cur->_left;}else if (kot(cur->_data) < kot(data)){parent = cur;cur = cur->_right;}else{return make_pair(Iterator(cur,_root),false);}}cur = new Node(data);Node* newnode = cur;cur->_col = Red;if (kot(parent->_data) < kot(data)){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;//如果父亲结点是红的while (parent && parent->_col == Red){Node* grandfather = parent->_parent;if (parent == grandfather->_left){//   g// p   u//Node* uncle = grandfather->_right;//u存在且为红if (uncle && uncle->_col == Red){//变色parent->_col = Black;uncle->_col = Black;grandfather->_col = Red;//继续向上处理cur = grandfather;parent = cur->_parent;}else{//uncle不存在，或者存在且为黑if (cur == parent->_left){// 旋转+变色//    g//  p   u//cRotateR(grandfather);parent->_col = Black;grandfather->_col = Red;}else{// 双旋转+变色//    g//  p   u//    cRotateL(parent);RotateR(grandfather);cur->_col = Black;//cur做了这棵树的根grandfather->_col = Red;}break;}}else{//	 g// u   p//Node* uncle = grandfather->_left;// 叔叔存在且为红 变色即可if (uncle && uncle->_col == Red){parent->_col = Black;uncle->_col = Black;grandfather->_col = Red;//继续向上处理cur = grandfather;parent = cur->_parent;}else//uncle不存在，或者存在且为黑{// 旋转+变色//    g//  u   p//         cif (cur == parent->_right){RotateL(grandfather);parent->_col = Black;grandfather->_col = Red;}else{// 双旋转+变色//    g//  u   p//    cRotateR(parent);RotateL(grandfather);cur->_col = Black;grandfather->_col = Red;}break;}}}_root->_col = Black;//不返回cur是因为旋转后cur可能已经不在原位//所以newnode记录新节点并返回//return make_pair(Iterator(cur,_root),true);return make_pair(Iterator(newnode,_root),true);}bool Check(Node* root, int BlackNum, const int refNum){// blackNum 根到当前结点的黑结点的数量if (root == nullptr){// 前序遍历走到空时，意味着一条路径走完了if (BlackNum != refNum){cout << "存在黑色结点的数量不相等的路径" << endl;return false;}return true;}//检查父亲if (root->_col == Red && root->_parent->_col == Red){cout << root->_kv.first << "存在连续的红结点" << endl;return false;}if (root->_col == Black){BlackNum++;}return Check(root->_left, BlackNum, refNum) && Check(root->_right, BlackNum, refNum);}bool IsBalance(){if (_root == nullptr){return true;}if (_root->_col == Red){return false;}Node* cur = _root;int refNum = 0; // 参考值 while (cur){if (cur->_col == Black)++refNum;cur = cur->_left;}return Check(_root, 0, refNum);}Iterator Find(const K& key){Node* cur = _root;while (cur){if (cur->_kv.first < key){cur = cur->_right;}else if (cur->_kv.first > key){cur = cur->_left;}else{return Iterator(cur,_root);}}return end();}void InOrder(){_InOrder(_root);cout << endl;}int Height(){return _Height(_root);}int Size(){return _Size(_root);}protected:int _Size(Node* root){if (root == nullptr)return 0;return _Size(root->_left) + _Size(root->_right) + 1;}int _Height(Node* root){if (root == nullptr)return 0;int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* ppNode = parent->_parent;subL->_right = parent;parent->_parent = subL;//if (ppNode == nullptr)if (parent == _root){_root = subL;subL->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* parentParent = parent->_parent;subR->_left = parent;parent->_parent = subR;if (parentParent == nullptr){_root = subR;subR->_parent = nullptr;}else{if (parent == parentParent->_left){parentParent->_left = subR;}else{parentParent->_right = subR;}subR->_parent = parentParent;}}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_InOrder(root->_right);}
private:Node* _root = nullptr;
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
如若转载，请注明出处：http://www.pswp.cn/pingmian/95415.shtml
繁体地址，请注明出处：http://hk.pswp.cn/pingmian/95415.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

以OWTB为核心以客户为基础的三方仓运配一体化平台分析V0.2

以OWTB为核心以客户为基础的三方仓运配一体化平台分析V0.2

一、系统概述以OWTB&#xff08;Order-Warehouse-Transportation-Billing&#xff0c;订单-仓储-运输-结算&#xff09;为核心的三方仓运配一体化平台&#xff0c;是专为第三方物流企业打造的深度定制化解决方案。该平台以第三方仓运配为主线&#xff0c;以多客户/多SKU/个性化…
阅读更多...
技术框架之脚手架实现

技术框架之脚手架实现

一、 序言在日常的企业级Java开发中&#xff0c;我们经常会发现自己在重复地做着一些项目初始化工作&#xff1a;创建相似的项目结构、引入一堆固定的依赖包、编写通用的配置文件、拷贝那些几乎每个项目都有的基础工具类和日志配置。这些工作不仅枯燥乏味&#xff0c;而且容易出…
阅读更多...
小迪安全v2023学习笔记（七十七讲）—— 业务设计篇隐私合规检测重定向漏洞资源拒绝服务

小迪安全v2023学习笔记（七十七讲）—— 业务设计篇隐私合规检测重定向漏洞资源拒绝服务

文章目录前记WEB攻防——第七十七天业务设计篇&隐私合规检测&URL重定向&资源拒绝服务&配合项目隐私合规 - 判断规则&检测项目介绍案例演示URL重定向 - 检测判断&钓鱼配合介绍黑盒测试看业务功能看参数名goole语法搜索白盒测试跳转URL绕过思路钓鱼配合资…
阅读更多...
用AI做旅游攻略，真能比人肉整理靠谱？

用AI做旅游攻略，真能比人肉整理靠谱？

大家好&#xff0c;我是极客团长&#xff01; 作为一个沉迷研究 “AI 工具怎么渗透日常生活” 的科技博主&#xff0c;我开了个 AI 解决生活小事系列。 前两期聊了用 AI 写新闻博客、扒商业报告&#xff0c;后台一堆人催更&#xff1a;能不能搞点接地气的&#xff1f;比如&am…
阅读更多...
Axure RP 9 Mac 交互原型设计

Axure RP 9 Mac 交互原型设计

原文地址&#xff1a;Axure RP 9 Mac 交互原型设计 安装教程 Axure RP 9是一款功能强大的原型设计和协作工具。 它不仅能够帮助用户快速创建出高质量的原型设计&#xff0c;还能促进团队成员之间的有效协作&#xff0c;从而极大地提高数字产品开发的效率和质量。 拥有直观易…
阅读更多...
多线程——线程状态

多线程——线程状态

目录 1.线程的状态 1.1 NEW 1.2 RUNNABLE 1.3 BLOCKED 1.4 WAITING 1.5 TIMED_WAITING 1.6 TERMINATED 2.线程状态的相互转换 在上期的学习中&#xff0c;已经理解线程的启动&#xff08;start()&#xff09;、休眠&#xff08;sleep()&#xff09;、中断&#xff08;i…
阅读更多...
IMX6ULL的设备树文件简析

IMX6ULL的设备树文件简析

先分析一个完整的设备树&#xff0c;是怎么表达各种外设信息的。以imux6ull开发板为例进行说明。这个文件里就一个设备信息才这么点内容&#xff0c;是不是出问题了&#xff1f;当然不是&#xff0c;我们知道dts文件是可包含的&#xff0c;所以&#xff0c;最终形成的一个完整文…
阅读更多...
【ARM】PACK包管理

【ARM】PACK包管理

1、 文档目标对 pack 包的管理有更多的了解。2、 问题场景客户在安装了过多的 pack 包导致软件打开比较慢&#xff0c;各种 pack 包颜色的区别&#xff0c;及图标不同。3、软硬件环境1&#xff09;、软件版本&#xff1a;Keil MDK 5.392&#xff09;、电脑环境&#xff1a;Wind…
阅读更多...
【Kubernetes】知识点4

【Kubernetes】知识点4

36. 说明K8s中Pod级别的Graceful Shutdown。答&#xff1a;Graceful Shutdown&#xff08;优雅关闭&#xff09;是指当 Pod 需要终止时&#xff0c;系统给予运行中的容器一定的时间来等待业务的应用的正常关闭&#xff08;如保存数据、关闭连接、释放资源等&#xff09;&#x…
阅读更多...
Paraverse平行云实时云渲染助力第82届威尼斯电影节XR沉浸式体验

Paraverse平行云实时云渲染助力第82届威尼斯电影节XR沉浸式体验

今年&#xff0c;Paraverse平行云实时云渲染平台LarkXR&#xff0c;为享有盛誉的第82届威尼斯国际电影节&#xff08;8月27日至9月6日&#xff09;带来沉浸式体验。 LarkXR助力我们的生态伙伴FRENCH TOUCH FACTORY&#xff0c;实现ITHACA容积视频的XR交互演示&#xff0c;从意大…
阅读更多...
大数据开发计划表（实际版）

大数据开发计划表（实际版）

太好了&#xff01;我将为你生成一份可打印的PDF版学习计划表&#xff0c;并附上项目模板与架构图示例&#xff0c;帮助你更直观地执行计划。 由于当前环境无法直接生成和发送文件&#xff0c;我将以文本格式为你完整呈现&#xff0c;你可以轻松复制到Word或Markdown中&#xf…
阅读更多...
GitLab 18.3 正式发布，更新多项 DevOps、CI/CD 功能【二】

GitLab 18.3 正式发布，更新多项 DevOps、CI/CD 功能【二】

沿袭我们的月度发布传统&#xff0c;极狐GitLab 发布了 18.3 版本&#xff0c;该版本带来了通过直接转移进行迁移、CI/CD 作业令牌的细粒度权限控制、自定义管理员角色、Kubernetes 1.33 支持、通过 API 让流水线执行策略访问 CI/CD 配置等几十个重点功能的改进。下面是对部分重…
阅读更多...
Docker学习笔记（二）：镜像与容器管理

Docker学习笔记（二）：镜像与容器管理

Docker 镜像 最小的镜像 hello-world 是 Docker 官方提供的一个镜像&#xff0c;通常用来验证 Docker 是否安装成功。 先通过 docker pull 从 Docker Hub 下载它。 [rootdocker ~]# docker pull hello-world Using default tag: latest latest: Pulling from library/hello-wor…
阅读更多...
STM32F103C8T6开发板入门学习——寄存器和库函数介绍

STM32F103C8T6开发板入门学习——寄存器和库函数介绍

学习目标&#xff1a;STM32F103C8T6开发板入门学习——寄存器和库函数介绍学习内容&#xff1a; 1. 寄存器介绍 1.1 存储器映射 存储器本身无固有地址&#xff0c;是具有特定功能的内存单元。它的地址是由芯片厂商或用户分配&#xff0c;给存储器分配地址的过程就叫做存储区映射…
阅读更多...
【CouponHub项目开发】使用RocketMQ5.x实现延时修改优惠券状态，并通过使用模板方法模式重构消息队列发送功能

【CouponHub项目开发】使用RocketMQ5.x实现延时修改优惠券状态，并通过使用模板方法模式重构消息队列发送功能

在上个章节中我实现了创建优惠券模板的功能&#xff0c;但是&#xff0c;优惠券总会有过期时间&#xff0c;我们怎么去解决到期自动修改优惠券状态这样一个功能呢&#xff1f;我们可以使用RocketMQ5.x新出的任意定时发送消息功能来解决。 初始方案&#xff1a;首先在创建优惠券…
阅读更多...
Claude Code SDK 配置Gitlab MCP服务

Claude Code SDK 配置Gitlab MCP服务

一、MCP配置前期准备 &#xff08;一&#xff09;创建个人令牌/群组令牌 我这里是创建个人令牌&#xff0c;去到首页左上角&#xff0c;点击头像——>偏好设置——>访问令牌——>添加新令牌 &#xff08;二&#xff09;配置mcp信息 去到魔塔社区&#xff0c;点击mc…
阅读更多...
Eclipse 常用搜索功能汇总

Eclipse 常用搜索功能汇总

Eclipse 常用搜索功能汇总 Eclipse 提供了多种搜索功能&#xff0c;帮助开发者快速定位代码、文件、类、方法、API 等资源。以下是详细的使用方法和技巧。 一、常用搜索快捷键快捷键功能描述Ctrl H打开全局搜索对话框&#xff0c;支持文件、Java 代码、任务等多种搜索。Ctrl …
阅读更多...
关于Spring的一些理解

关于Spring的一些理解

Spring整体结构&#xff1a;Spring实际运行场景&#xff1a;基础 Spring启动过程 传统Spring&#xff1a; &#xff08;1&#xff09;初始化准备阶段 &#xff08;2&#xff09;容器创建与注入 &#xff08;3&#xff09;Bean工厂后置处理 &#xff08;4&#xff09;Bean工厂后…
阅读更多...
Windows右下角系统托盘图标快速显示或隐藏

Windows右下角系统托盘图标快速显示或隐藏

系统托盘指的是Windows电脑桌面右下角的区域&#xff0c;包括时间、wifi&#xff08;网络&#xff09;、音量、电源、输入法、一些程序/应用等。启动了应用后&#xff0c;Windows会把部分应用的图标显示或隐藏在系统托盘区。我们可以根据需要快速显示或隐藏相关应用&#xff0c…
阅读更多...
Kotlin编程学习记录2

Kotlin编程学习记录2

Kotlin编程学习记录2——条件与循环 条件语句&#xff1a;if 与 when ​ Kotlin 的控制流把“表达式优先”作为设计原则——if、when 不只是控制语句&#xff0c;都可以作为表达式使用并返回值&#xff0c;这影响了日常代码风格&#xff08;更函数式、可组合&#xff09;。笔…
阅读更多...
最新文章

Copyright @ 2022~2023