2025.9.5

226. 翻转二叉树

题目

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1：

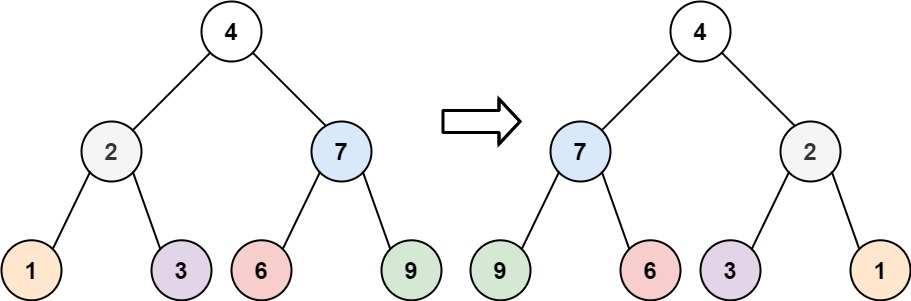
输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

示例 2：

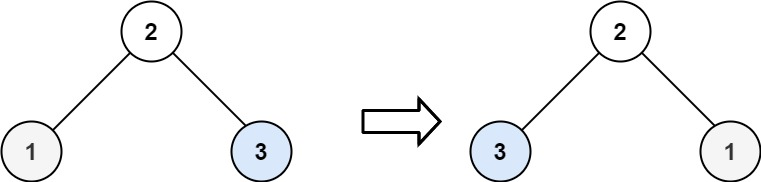
输入：root = [2,1,3]
输出：[2,3,1]

示例 3：

输入：root = []
输出：[]

提示：

树中节点数目范围在 [0, 100] 内
-100 <= Node.val <= 100

总体思路

使用递归的深度优先搜索 DFS方法来翻转二叉树。其核心思想是：

1. 递归地翻转左子树
2. 递归地翻转右子树
3. 交换当前节点的左右子节点
4. 基础情况：当节点为空时，直接返回（递归终止条件）

这种后序遍历的方式确保在交换当前节点的子节点之前，其左右子树都已经被正确翻转。

时间复杂度与空间复杂度

时间复杂度：O(n)

• 每个节点恰好被访问一次，n为二叉树中的节点数量
• 每个节点进行常数时间的操作（交换指针）

空间复杂度：O(h)，其中h是树的高度

• 空间复杂度主要由递归调用栈的深度决定
• 在最坏情况下（树退化为链表），h = n，空间复杂度为O(n)
• 在最好情况下（平衡二叉树），h = logn，空间复杂度为O(logn)
• 平均情况下，空间复杂度为O(h)

代码

golang

/*** Definition for a binary tree node.* type TreeNode struct {*     Val int*     Left *TreeNode*     Right *TreeNode* }*/
func invertTree(root *TreeNode) *TreeNode {if root == nil {return root}root.Left = invertTree(root.Left)root.Right = invertTree(root.Right)root.Left, root.Right = root.Right, root.Leftreturn root
}

/*** Definition for a binary tree node.* type TreeNode struct {*     Val int*     Left *TreeNode*     Right *TreeNode* }*/
func invertTree(root *TreeNode) *TreeNode {// 基础情况：如果当前节点为空，直接返回// 这是递归的终止条件，空节点不需要翻转if root == nil {return root}// 递归地翻转左子树// 将左子树完全翻转后，返回翻转后的左子树根节点root.Left = invertTree(root.Left)// 递归地翻转右子树// 将右子树完全翻转后，返回翻转后的右子树根节点root.Right = invertTree(root.Right)// 交换当前节点的左右子节点// 使用Go的多重赋值特性，不需要临时变量root.Left, root.Right = root.Right, root.Left// 返回翻转后的当前子树根节点return root
}

101. 对称二叉树

题目

给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1：

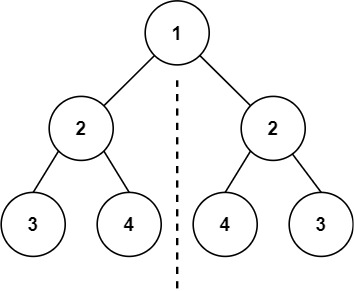
输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

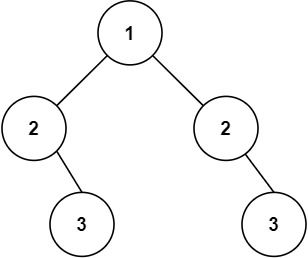
输入：root = [1,2,2,null,3,null,3]
输出：false

提示：

树中节点数目在范围 [1, 1000] 内
-100 <= Node.val <= 100

进阶：你可以运用递归和迭代两种方法解决这个问题吗？

总体思路

这段代码使用**广度优先搜索（BFS）**的方法来判断二叉树是否轴对称（镜像对称）。其核心思想是：

1. 将需要比较的节点成对放入队列中（左子树的左节点 vs 右子树的右节点，左子树的右节点 vs 右子树的左节点）
2. 每次从队列中取出一对节点进行比较
3. 如果所有对应的节点对都满足镜像关系，则二叉树是对称的

时间复杂度与空间复杂度

时间复杂度：O(n)

• 每个节点最多被访问一次，n为二叉树中的节点数量
• 每个节点进行常数时间的比较操作

空间复杂度：O(n)

• 在最坏情况下（完全二叉树），队列中最多会存储约n/2个节点对
• 空间复杂度主要由队列的大小决定

代码

golang

/*** Definition for a binary tree node.* type TreeNode struct {*     Val int*     Left *TreeNode*     Right *TreeNode* }*/
func isSymmetric(root *TreeNode) bool {if root == nil {return true}type pair struct{l, r *TreeNode}q := []pair{{root.Left, root.Right}}for len(q) > 0 {p := q[0]q = q[1:]left, right := p.l, p.rif left == nil && right == nil {continue}if left == nil || right == nil {return false}if left.Val != right.Val {return false}q = append(q,pair{left.Left,right.Right})q = append(q, pair{left.Right, right.Left})}return true
}

package maintype TreeNode struct {Val   intLeft  *TreeNodeRight *TreeNode
}// isSymmetric 判断二叉树是否轴对称（镜像对称）
func isSymmetric(root *TreeNode) bool {// 如果根节点为空，空树被认为是对称的if root == nil {return true}// 定义pair结构体来存储需要比较的一对节点// l: 左子树中的某个节点，r: 右子树中对应的镜像节点type pair struct{ l, r *TreeNode }// 初始化队列，首先将根节点的左右子节点作为第一对需要比较的节点q := []pair{{root.Left, root.Right}}// 当队列不为空时循环处理for len(q) >  {// 从队列头部取出一对节点p := q[0]q = q[1:]  // 移除队列头部元素left, right := p.l, p.r// 如果两个节点都为空，说明对称，继续检查其他节点对if left == nil && right == nil {continue}// 如果只有一个节点为空，另一个不为空，说明不对称if left == nil || right == nil {return false}// 如果两个节点都不为空，但值不相等，说明不对称if left.Val != right.Val {return false}// 将下一层需要比较的节点对加入队列：// 1. 左节点的左子节点 vs 右节点的右子节点（外侧比较）// 2. 左节点的右子节点 vs 右节点的左子节点（内侧比较）q = append(q, pair{left.Left, right.Right})q = append(q, pair{left.Right, right.Left})}// 如果所有节点对都通过检查，说明二叉树是对称的return true
}

知识点

q := []pair{{root.Left, root.Right}}

这一行是 Go 语言里“构造切片并初始化第一个元素”的写法，拆开来看就明白了：

1. []pair{ ... }
   表示创建一个元素类型为 pair 的切片（slice）。
2. {{root.Left, root.Right}}
   切片里只放 一个元素，这个元素又是一个 pair 结构体，所以用两层花括号：
   • 外层 {} 是“切片字面量”；
   • 内层 {} 是“结构体字面量”，给 pair 的字段 l、r 分别赋值为 root.Left 和 root.Right。

等价于：

q := make([]pair, 0, 1)
q = append(q, pair{l: root.Left, r: root.Right})

只是第一种写法更简洁，常用来一次性初始化切片。