---

---

一、二叉搜索树（排序树）

1. 概念初识

我们二叉搜索树有以下几个特点，即

1. 左子树不为空时，左子树节点值都小于根节点的值
2. 右子树不为空时，右子树节点值都大于根节点的值
3. 并且对于左右子树来看，其子树也是满足这两个条件

当我们对这个二叉搜索树进行中序遍历后，得到的就是一个有序的值的集合
以下是这种搜索树的示例

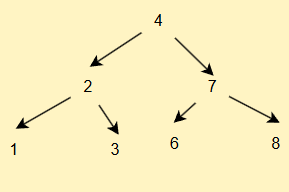
我们进行中序遍历后得到的结果是1 2 3 4 6 7 8

好，当我们插入节点的时候，就不需要去遍历全部的节点了
如果我们插入的节点它的值大于根节点，说明要去右边插入，否则就是左边
比如我想插入9这个节点，直接去根节点为8的右树 插入即可 `
这样就提高了插入效率，类似于“二分”

但是你是否想过一种极端情况，它因为所有节点都是升序的，会变成一颗单分支的树，1-->2-->3，这样就会退化成n的时间复杂度

因此我们定义的二叉搜索树，左右树的高度不能超过1
对于1-->2-->3也不是没有解决办法，我们可以把其进行旋转，这样就可以变成
2
/ \
1 3
有很多种旋转，比如左旋，右旋，或者是双旋，我们熟知的红黑树就是旋转得来的，再加上颜色的标记

2. 模拟实现

1. 创建搜索树节点

static class TreeNode{public int val;public TreeNode left;public TreeNode right;public TreeNode(int val) {this.val = val;}}public TreeNode root;

2. 查找指定元素是否存在

//查找方法public boolean search(int val){if(root == null){return false;}TreeNode current = root;while(current != null){if(current.val < val){current = current.right;}else if(current.val > val){current = current.left;}else{return true;}}return false;}

3. 插入

我们通过之前的概念演示不难看出，我们插入的节点一般都是在叶子节点插入的

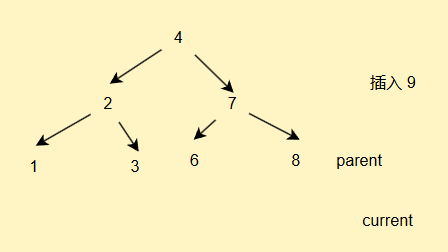
//插入方法public void insert(int val){if(root == null){//说明根节点就是我们的新节点root = new TreeNode(val);return;}//我们插入节点要定义一个双亲节点保存信息//因为我们最后current会走到空的位置，//循环不好出来，此时不好连接TreeNode current = root;TreeNode parent = null;while(current != null){if(current.val > val){parent = current;current = current.left;}else if(current.val < val){parent = current;current = current.right;}else{//重复的值我们不进行存储return;}}TreeNode newNode = new TreeNode(val);//为什么不用判断等于，因为等于的情况我们前面已经return走了if(parent.val > val){parent.left = newNode;}else{parent.right = newNode;}}

4. 删除

这个有点难度，我们得分情况讨论

如果current.left == null

1. 如果current == root，直接root = cur.right
   
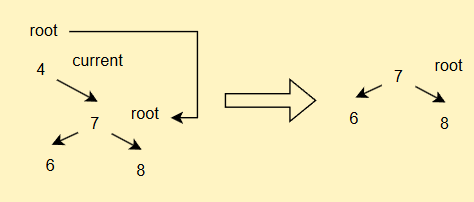
2. 如果current不为root，但是其为parent的左子树
   
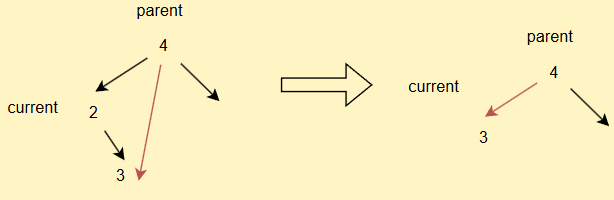
3. 如果current不为root，但是其为parent的右子树
   

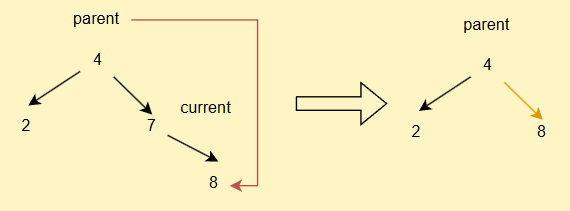
同理，如果current.right == null

1. 如果current == root，直接root = current.left
   
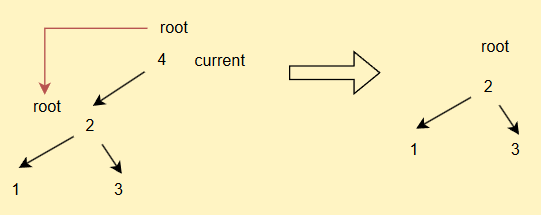
2. 如果current不为root，但是其为parent的左子树，直接parent.left = current.left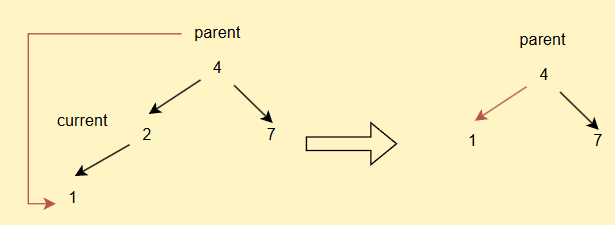
3. 如果current不为root，但是其为parent的右子树，直接parent.right = current.left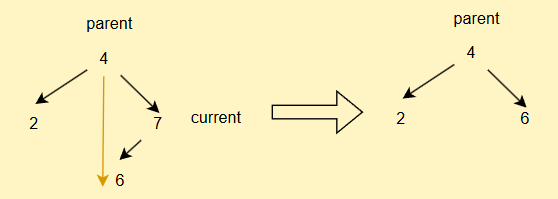

现在，我们处理最棘手的一种情况，即current.left != null && current.left != null
我们要使用替换的思想，而不是真的把目标节点删除，因为我们要保证删除后新的节点的左树小于当前节点值，右树大于当前节点值
因此我们要在右树的左子树搜索最小值，放在当前要删除的节点的位置（或者在左树的右子树中搜寻最大值放在要删除的节点的位置）
因此我们还需要两个遍历，一个是找到最大值的节点的引用target，一个是找到最大值的节点其双亲节点的引用targetParent

//删除方法public void remove(int val) {TreeNode current = root;TreeNode parent = null;while (current != null) {if (current.val > val){parent = current;current = current.left;}else if(current.val < val){parent = current;current = current.right;}else{removeNode(current,parent);return;}}}private void removeNode(TreeNode current,TreeNode parent) {if (current.left == null) {if (current == root) {root = current.right;} else if (current == parent.left) {parent.left = current.right;} else if (current == parent.right) {parent.right = current.right;}} else if (current.right == null) {if (current == root) {root = current.left;} else if (current == parent.left) {parent.left = current.left;} else if (current == parent.right) {parent.right = current.left;}}else{TreeNode target = current;TreeNode targetParent = null;//寻找左树中的最小值while(target.left != null){targetParent = target;target = target.left;}current.val = target.val;targetParent.left = target.right;}}

但是我想告诉你，这段代码有个小错误，在这里

TreeNode target = current;
TreeNode targetParent = null;
//寻找左树中的最小值
while(target.left != null){targetParent = target;target = target.left;
}
current.val = target.val;
targetParent.left = target.right;

为什么？你看，如果我们遇到这种情况

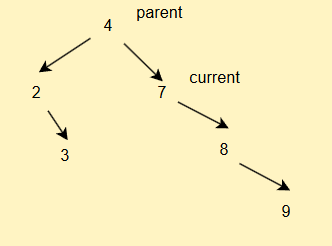
此时targetParent.left = target.right会导致节点错放的问题

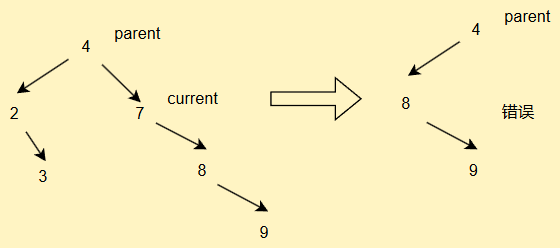
因此要加以判断

if(target == targetParent.right) {targetParent.right = target.right;
}else{targetParent.left = target.right;
}

自定义一个测试类Test

public static void main(String[] args) {TreeNodeTest treeNodeTest = new TreeNodeTest();//创建节点，插入值int [] test = new int[10];for (int i = 0; i < test.length; i++) {test[i] += 2*i;}for(int x:test){treeNodeTest.insert(x);}//查询值是否存在System.out.println(treeNodeTest.search(10));//删除值treeNodeTest.remove(10);//查询值是否存在System.out.println(treeNodeTest.search(10));}

二、Map类

Map类它是一个独立的接口，不继承Collection类，我们之前右讲过哈希表，内部具有映射关系
我们现在就以单词String和这个单词出现的频次Integer来探究这种映射关系
我们新建一个类Map<String,Integer> map = new TreeMap<>();
我们TreeMap其底层就是一个二叉搜索树，HashMap我们之后再讲

我们讲几个常用的方法，以我们刚刚的单词例子

1. put——设置单词以及其频次

map.put("zlh",5);
map.put("hello",1);
map.put("hi",3);

2. get——获取单词频次

System.out.println(map.get("zlh"));//5
System.out.println(map.get("hello"));//1

3. getOrDefault——获取单词频次或返回默认值

这个方法就是如果我们获取的单词不存在，就返回默认值，默认值可以自己设定

System.out.println(map.getOrDefault("hi",999));//3
System.out.println(map.getOrDefault("lll",6666));//6666

4. remove——删除单词频次信息

map.remove("hi");
System.out.println(map.getOrDefault("hi",1111));//1111

5. keySet——取出单词放入大集合Set中

这个大集合Set因为不能有重复元素，因此可以有去重效果

Set<String> set;
set = map.keySet();
System.out.println(set);//[hello, zlh]

6. values——取出对应单词频次放入Collection中

这个Collection可以有重复元素，而且这个是一个数集

map.put("cheerful",5);
Collection<Integer> collection;
collection = map.values();
System.out.println(collection);//[5, 1, 5]

7. containsKey——查看单词是否存在

System.out.println(map.containsKey("zlh"));//true

8. containsValue——查看频次是否存在

System.out.println(map.containsValue(999999));//false

9. entrySet——返回所有的映射关系

Set<Map.Entry<String,Integer>> sets = map.entrySet();
for(Map.Entry<String,Integer> es : sets){//强遍历String str = es.getKey();System.out.print(str+" ");Integer val = es.getValue();System.out.println(val+" ");
}

10. 注意事项

1. 就跟哈希表一样的，单词不可以重复，频次可以重复
2. 单词不可以是空的单词map.put(null,5)，因为底层谁白了也是一颗树，树连节点引用都没有，谈何赋值
3. Map中的Key和Value根据刚刚到演示，看到是可以分离出的

三、Set类

因为Set类继承了Collection类，并且是一个数集，因此只可以存入Value

Set<Integer> set = new TreeSet<>();

我们随便举几个例子，说明其内部的方法

1. add——添加元素

我们是不可以添加重复元素的

set.add(11);

2. contains、clear、remove、size、isEmpty、toArray

分别是检测是否存在，清空，删除，求大小，检测是否是空的，转换成数组

System.out.println(set.contains(11));//true
set.remove(11);
System.out.println(set.size());//1
System.out.println(set.isEmpty());//false
System.out.println(Arrays.toString(set.toArray()));//[999]
set.clear();
System.out.println(set.isEmpty());//true

我们点开TreeSet的源码，发现其底层实现的是TreeMap，这样就保证了集合的数据唯一性

我们不光可以new TreeSet，还可以new LinkedList，这是一个双向链表的集合

四、哈希表（又称散列表）

1. 哈希冲突

我们在放入元素的时候，一般是要去寻找其位置放哪，但是如果我定义一个哈希表长度为10，下标从0~9
那我放入两个元素2和12，我们根据%10求的结果都要放入1下标，此时冲突就产生了

2. 避免哈希冲突

1. 设计哈希函数

我们运用的是除留余数法，即*表中地址数为m，取出一个不大于m的最接近或者是等于m的质数作为除数p，则公式$Hash(Key) = key % p，讲计算结果的关键码转为哈希地址
还有String类中的hashCode方法解决字符串冲突以及Integer中的hashCode方法解决数值冲突

2. 直接定制

我们通常需要设计一个合理的哈希函数，还记得我们之前经常使用的模拟哈希表吗，比如统计字符出现次数
而我们都是-='a'去计算偏移量的

3. 调整负载因子

举个例子，如果是数组，我们就进行扩容操作

3. 解决哈希冲突

1. 闭散列

一般在发生哈希冲突的时候，哈希表是没有满的，因此其必定是有空位置的，我们可以把冲突Key值放入其下一个空的位置中去
每次放的时候，我们都探测一下，这个探测是线性的

但是这样放那面太集中了，容易把冲突的元素放在一块，因此我们给出个优化方法
Hi = (H0+i^2)%m，i代表第几次放入，H0代表第一次放入的位置（不冲突时候），m代表这个表的长度

因此，闭散列无需额外空间就可以删除，而且结果存储是连续的，而且不需要指针去引用
但是，尽管有刚刚的优化方法，还是会导致冲突元素的聚集，而且删除有一个很麻烦的事情
就比如我们刚刚到表，假设我们把2删除后，谁去下标2的位置，而且我们也不知道下标2的元素删没删
因此我们要在各个下标定义标记，为0和1，但是这样继续进来元素，又会导致二次聚集，因此闭散列不可靠，也很不效率

2. 开散列（又称散列桶/哈希桶）

我们采用大小集合结合的方式，我们每一个下标都存入一个小集合，形成映射关系
冲突的元素全部都放入小集合中，如果小集合内部冲突元素太多，我们就把其转换成搜索树或者是哈希函数的再设计

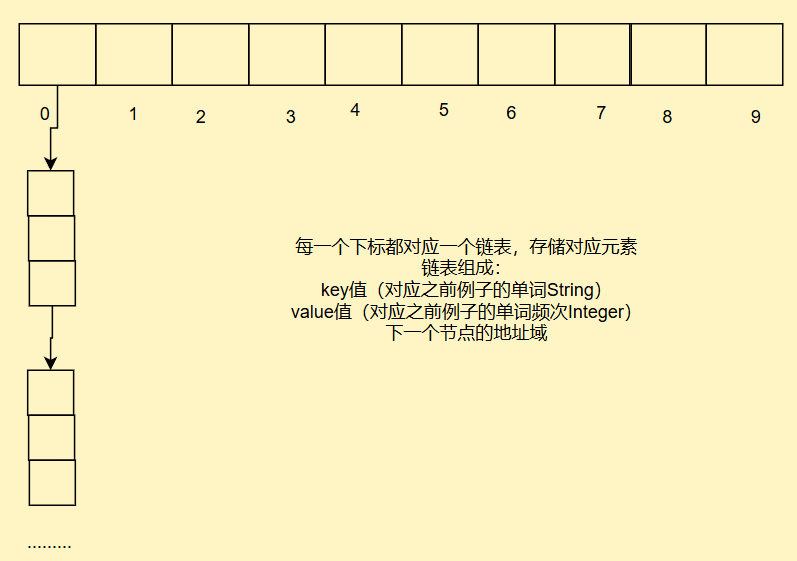
自定义一个类MapAndSetTest实现模拟表

static class Node{public int key;//对应之前例子中单词Stringpublic int val;//对应之前例子中单词频次Integerpublic Node next;//下一节点的地址域public Node(int key, int val) {this.key = key;this.val = val;}}public Node[] array;//表数组public int usedSize;//有效元素个数，用来计算负载因子public double load = 0.75;//默认负载因子大小public MapAndSetTest(){//建立表array = new Node[10];}

1. 插入元素
   如果数组满了要扩容，但是我们不能就简单的扩容，我们扩容之后，原本冲突的值我们要重新规划其放的位置
   比如原本大小为10下标0~9的这个表中，在下标2存放了2,12
   扩容后到了大小为20下标0~19，因此我们要把下标2中的12存入下标12

因此说白了就是扩容后要把表中所有下标的所有元素重新遍历放入新的下标中

//加入元素public void put(int key,int val){//先找到下标位置//找到位置后看看是否和已有的key值重复//不重复的话就采用头插法（尾插也可以）int index = key % array.length;Node current = array[index];while(current != null){if(current.key == key){//如果出现重复的key值，我们就更新内部的value就好current.val = val;}current = current.next;}//说明不存在key值，执行头插操作Node insertNode = new Node(key,val);insertNode.next = array[index];array[index] = insertNode;this.usedSize++;//插入后检查负载因子，如果超过限定额度要进行扩容if(isFull() >= load){//扩容grow();}}private double isFull(){return usedSize*1.0/array.length;//*1.0是为了转换成小数计算}private void grow() {//此时我们先创造一个空的表Node [] newArray = new Node[array.length*2];//遍历原表中的所有下标的所有元素for (int i = 0; i < array.length; i++) {Node current = array[i];while(current != null){int newIndex = current.key% newArray.length;//采用头插法在新的表中的对应下标插入元素//为了防止头茬后我们的current跑到别的下标的链表中去//因此我们要实现保存当前下标的后续链表的信息Node nextCurrent = current.next;current.next = newArray[newIndex];newArray[newIndex] = current;current = nextCurrent;}}//更新表this.array = newArray;}

2. 获取对应key值的value

//获取对应的key值的valuepublic int get(int key){int index = key%array.length;Node current = array[index];while(current != null){if(current.key == key){return current.val;}current = current.next;}return -1;}

3. 测试

public static void main(String[] args) {MapAndSetTest mapAndSetTest = new MapAndSetTest();int[] test = new int[5];Random random = new Random();for (int i = 0; i < test.length; i++) {test[i] = random.nextInt(25);}for (int x : test) {mapAndSetTest.put(x, x / 2);}//查看结果for (int i = 0; i < mapAndSetTest.array.length; i++) {Node current = mapAndSetTest.array[i];if (current != null) {System.out.print("Bucket " + i + ": ");while (current != null) {System.out.print("(" + current.key + "," + current.val + ") ");current = current.next;}System.out.println();}}//获取对应key值元素System.out.println(mapAndSetTest.get(22));}

---

文章错误不可避免，期待您的指正，我们共同进步

---

---

END