本文介绍了《企业IT系统全生命周期管理与运营平台建设方案》的项目内容，包括项目背景、蓝图架构、核心业务流程、系统总体架构、解决方案等。
重点内容：
1. 项目背景：介绍企业IT系统全生命周期管理的重要性。
2. 蓝图架构：描述项目的整体架构设计。
3. 核心业务流程：详述项目的主要流程，如需求管理、任务管理、测试管理等。
4. 系统总体架构：阐述系统的技术架构和组成模块。
5. 一阶段解决方案：介绍项目第一阶段的主要工作内容和成果，包括统一门户、需求任务管理、统一源代码管理等。
6. 二阶段解决方案：描述项目第二阶段的重点工作和目标，如项目立项管理、招投标管理等。
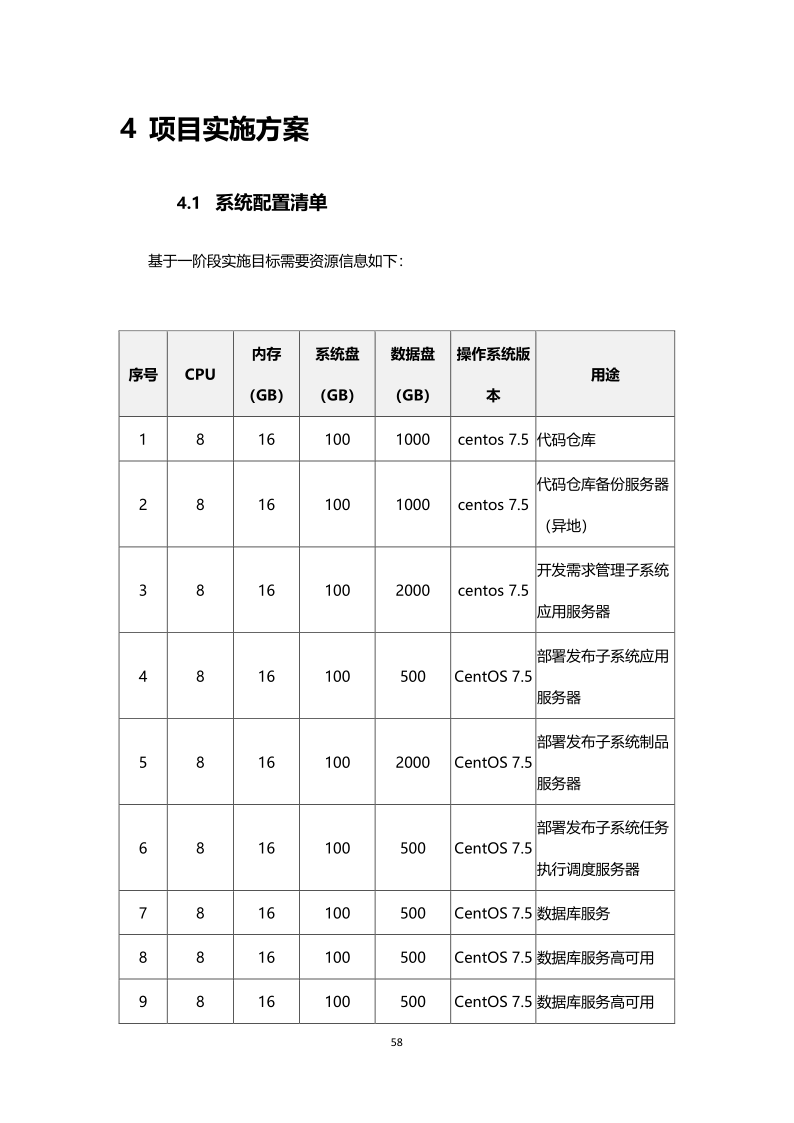
7. 项目实施方案：介绍项目的实施计划和步骤。