3D图像渲染和threejs交互坐标系入门知识整理

1. Games101

b站上面就有，看到第9节课基本对于图形渲染的原理和渲染过程有所了解。然后就可以使用openGL和GLSL。

点输入->投影到二维（生成三角形面）->光栅化为像素->z-buffer深度缓存判断层级->着色shading

2. openGL和GLSL

参考网站：https://www.shadertoy.com/
教程：https://learnopengl-cn.github.io/01%20Getting%20started/01%20OpenGL/
其他：
http://webgl3d.cn/pages/f66004/

3. 一些矩阵概念记录

点乘和叉乘

来自AI：

在图形学中，点乘（点积）和叉乘（叉积）是向量运算的基础，它们的方向判断和物理意义如下：

一、点乘（Dot Product）

1. 方向判断

公式：a⋅b=∣a∣∣b∣cosθ 其中θ是两向量的夹角。
符号含义：
正：θ < 90deg)（两向量方向大致相同）。
零：θ = 90deg)（两向量垂直）。
负：θ > 90deg)（两向量方向大致相反）。

2. 物理意义

投影关系：点乘结果等于向量a在b方向上的投影长度乘以b的模长。
能量传递：例如，光照计算中，光源方向与表面法线的点乘决定了光照强度（夹角越小，光照越强）。
相似性度量：用于判断两个向量的方向一致性（如判断物体是否面向光源）。

二、叉乘（Cross Product）

1. 方向判断

公式： a×b=∣a∣∣b∣sinθ⋅n 其中θ是两向量的夹角，n是垂直于a和b所在平面的单位向量。
方向规则（右手定则）：右手四指从a向b弯曲（夹角 < 180°），拇指指向即为叉乘结果的方向。

2. 物理意义

法向量生成：叉乘结果垂直于两向量所在平面，常用于计算平面法线（如3D建模中的多边形法线）。
面积计算：叉乘的模长等于两向量张成的平行四边形的面积。

三、图形学中的典型应用

1. 点乘的应用

光照模型：计算表面法线与光源方向的夹角，确定漫反射强度（如 Lambert 光照模型）。
背面剔除：判断多边形法线是否背离相机方向（点乘结果为负时剔除背面）。
向量归一化：点乘可快速计算向量长度的平方a⋅a=∣a∣^2。

2. 叉乘的应用

法线计算：由多边形的两个边向量叉乘得到面法线（如三角形面片的法向量）。
坐标系构建：在3D空间中，通过叉乘构建正交基向量（如切线、副切线和法线的 TBN 坐标系）。
碰撞检测：利用叉乘判断点是否在凸多边形内部（通过环绕测试）。

四、对比总结

运算 结果类型 方向规则 物理意义
点乘标量无方向，符号表示夹角投影、能量传递、相似性
叉乘向量右手定则确定垂直方向法向量、旋转趋势、面积

五、示例说明

点乘示例：若表面法线 n 与光源方向 L 的点乘为正，则该区域被照亮；若为负，则处于阴影中。

叉乘示例：在3D建模中，三角形顶点 (A, B, C) 的边向量AB和AC的叉乘可得到该三角形的法向量，用于渲染时的光照计算。

运算	结果类型	方向规则	物理意义
点乘	标量	无方向，符号表示夹角	投影、能量传递、相似性
叉乘	向量	右手定则确定垂直方向	法向量、旋转趋势、面积

通过点乘和叉乘的结合，图形学能够高效处理向量方向、空间关系和物理模拟等问题，是3D渲染和计算机图形学的核心工具。

4. 三维空间中的点击交互，坐标和点变换

有没有想过一个问题：你在屏幕上点了一个点，怎么映射到三维空间中的一个坐标？或者反过来，现在我们把物体放置在三维空间的一个位置，怎么知道用户在屏幕上的点击是不是点在这个物体上。
这就涉及三维空间中的坐标。可以看这个https://learnopengl-cn.github.io/01%20Getting%20started/08%20Coordinate%20Systems/

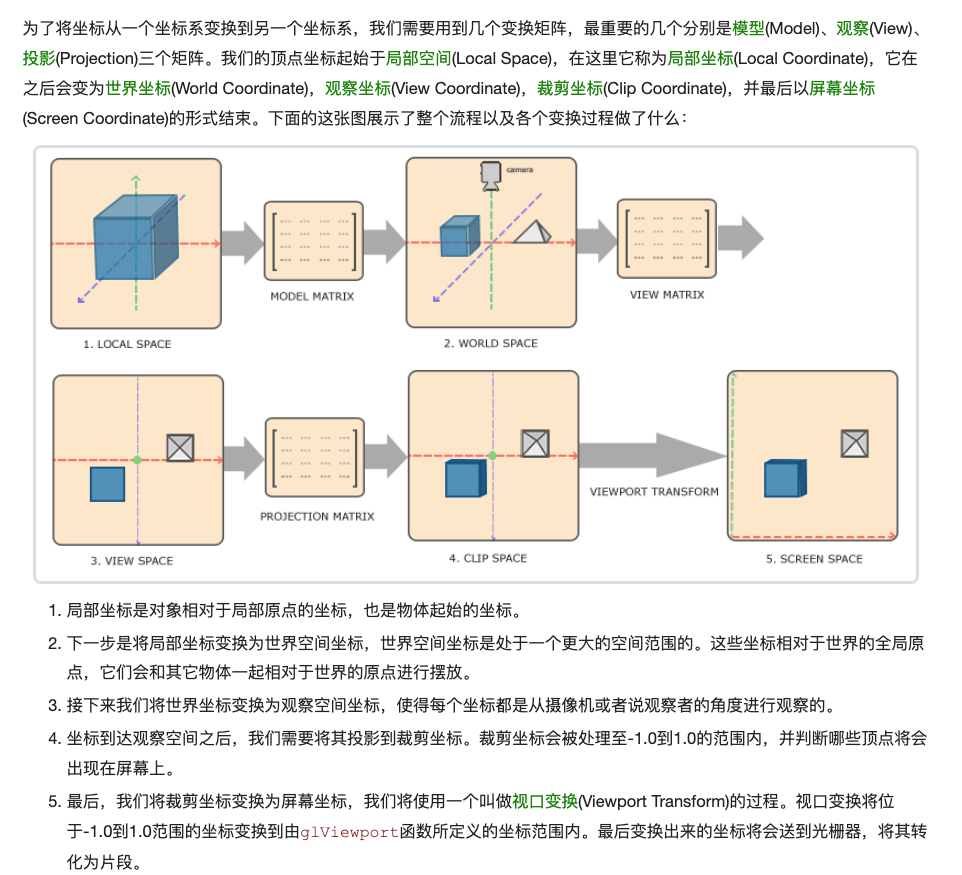
OpenGL希望在每次顶点着色器运行后，我们可见的所有顶点都为标准化设备坐标(Normalized Device Coordinate, NDC)。也就是说，每个顶点的x，y，z坐标都应该在-1.0到1.0之间，超出这个坐标范围的顶点都将不可见。我们通常会自己设定一个坐标的范围，之后再在顶点着色器中将这些坐标变换为标准化设备坐标。然后将这些标准化设备坐标传入光栅器(Rasterizer)，将它们变换为屏幕上的二维坐标或像素。

将坐标变换为标准化设备坐标，接着再转化为屏幕坐标的过程通常是分步进行的，也就是类似于流水线那样子。在流水线中，物体的顶点在最终转化为屏幕坐标之前还会被变换到多个坐标系统(CoordinateSystem)。
将物体的坐标变换到几个过渡坐标系(Intermediate CoordinateSystem)的优点在于，在这些特定的坐标系统中，一些操作或运算更加方便和容易，这一点很快就会变得很明显。对我们来说比较重要的总共有5个不同的坐标系统：

局部空间(Local Space，或者称为物体空间(Object Space))
世界空间(World Space)
观察空间(View Space，或者称为视觉空间(Eye Space))
裁剪空间(Clip Space)
屏幕空间(Screen Space)

Cube空间中的点和屏幕坐标的转换

因为我们在做全景交互展示，所以是一个Cube空间，然后有两个需求：

热点展示，AI带看。
屏幕点击，找到某个物品。

1. 热点展示，AI带看

一般有两种热点锚定方案：

直接使用三维空间中的热点坐标，判断如果当前用户屏幕上能看到热点了，给一些标注提示。

// 定义视口接口
interface Viewport {width: number;height: number;x: number;y: number;
}/*** 将方向向量投影到屏幕坐标* * 这个函数将三维空间中的方向向量转换为屏幕上的2D坐标，如果不在视图内返回undefined.* 使用相机的视图投影矩阵进行变换，并处理透视除法* * @param camera 透视相机对象* @param direction 归一化的方向向量* @param viewport 视口信息(可选，默认使用窗口尺寸)* @returns 屏幕坐标对象 {x, y} 或 undefined(如果在视锥外)*/
export function projectDirectionToScreen(camera: PerspectiveCamera,direction: Vector3,viewport?: Viewport
): { x: number; y: number } | undefined {// 设置默认视口if (!viewport) {viewport = {width: window.innerWidth,height: window.innerHeight,x: 0,y: 0};}// 创建齐次坐标点 (w=1)const worldPoint = new Vector4(direction.x, direction.y, direction.z, 1);// 计算视图投影矩阵 (投影矩阵 * 世界矩阵的逆)const viewProjectionMatrix = new Matrix4().multiplyMatrices(camera.projectionMatrix, camera.matrixWorldInverse);// 应用视图投影矩阵const clipSpaceCoords = worldPoint.clone().applyMatrix4(viewProjectionMatrix);// 透视除法 (将齐次坐标转换为三维坐标)const w = clipSpaceCoords.w;// 如果点在相机后方，返回undefinedif (w <= 0) return undefined;// 归一化设备坐标 (NDC) [-1, 1]const ndc = new Vector3(clipSpaceCoords.x / w,clipSpaceCoords.y / w,clipSpaceCoords.z / w);// 视锥体剔除 - 检查点是否在视锥体内if (Math.abs(ndc.x) > 1 || Math.abs(ndc.y) > 1 || ndc.z < -1 || ndc.z > 1) {return undefined;}// 转换为屏幕坐标return {x: (ndc.x + 1) * 0.5 * viewport.width + viewport.x,y: (1 - ndc.y) * 0.5 * viewport.height + viewport.y};
}// 热点管理插件
class AIHotspot {private camera: PerspectiveCamera;private renderer: THREE.WebGLRenderer;private hotspots: { position: Vector3; element: HTMLElement }[] = [];constructor(camera: PerspectiveCamera, renderer: THREE.WebGLRenderer) {this.camera = camera;this.renderer = renderer;}/*** 添加热点* @param position 热点在3D空间中的位置* @param content 热点显示的HTML内容*/addHotspot(position: Vector3, content: string) {const element = document.createElement('div');element.className = 'hotspot';element.innerHTML = content;document.body.appendChild(element);this.hotspots.push({ position, element });}/*** 更新热点位置*/update() {const viewport = this.renderer.getSize(new Vector2());for (const hotspot of this.hotspots) {// 计算热点在屏幕上的位置const screenPos = projectDirectionToScreen(this.camera,hotspot.position.clone().normalize(),{width: viewport.x,height: viewport.y,x: 0,y: 0});if (screenPos) {hotspot.element.style.display = 'block';hotspot.element.style.left = `${screenPos.x}px`;hotspot.element.style.top = `${screenPos.y}px`;} else {hotspot.element.style.display = 'none';}}}
}/** 使用：在animation中持续调用update判断就行 */
// 创建AI带看热点系统
const hotspotSystem = new AIHotspot(camera, renderer);// 添加热点
hotspotSystem.addHotspot(new Vector3(1, 0, 0), '<div class="hotspot">这里是热点！</div>'
);

由后端计算生成，给你一个UV位置。（这时候就需要UV坐标转方向向量，然后再转成屏幕位置）其实就是再加一步将UV坐标转成上面那一步的向量位置。

projectDirectionToScreen(cubeUVToDirection(CubeUVPos))

在这里插入图片描述

// 定义立方体UV坐标接口
interface CubeUV {faceIndex: number; // 立方体面索引 (0-5)u: number;         // 水平UV坐标 [0, 1]v: number;         // 垂直UV坐标 [0, 1]
}/*** 将立方体UV坐标转换为三维空间方向向量* * 这个函数将立方体纹理坐标(面索引和UV)转换为三维空间中的方向向量(单位向量)* 立方体面索引定义：* 0: 右 (+X)* 1: 左 (-X)* 2: 上 (+Y)* 3: 下 (-Y)* 4: 前 (+Z)* 5: 后 (-Z)* * @param cubeUV 立方体UV坐标对象* @returns 归一化的三维方向向量*/
export function cubeUVToDirection(cubeUV: CubeUV): Vector3 {const { faceIndex, u, v } = cubeUV;// 将UV从[0,1]映射到[-1,1]const uc = u * 2 - 1;const vc = v * 2 - 1;let x, y, z;// 根据面索引计算方向switch (faceIndex) {case 0: // 右 (+X)x = 1;y = -vc; z = -uc;break;case 1: // 左 (-X)x = -1;y = -vc;z = uc;break;case 2: // 上 (+Y)x = uc;y = 1;z = vc;break;case 3: // 下 (-Y)x = uc;y = -1;z = -vc;break;case 4: // 前 (+Z)x = uc;y = -vc;z = 1;break;case 5: // 后 (-Z)x = -uc;y = -vc;z = -1;break;default:break; // 无效的面索引}// 创建向量并归一化const direction = new Vector3(x, y, z);return direction.normalize();/** * direction.normalize将这个向量“归一化”，也就是把长度（模）变成 1，只保留方向信息。* 归一化后的向量叫做单位向量，常用于表示方向，而不关心距离大小。* * 场景意义* 在三维图形/全景/射线等场景中，归一化方向向量可以方便地进行投影、旋转、相交等运算。* 例如：你要从立方体的某个面上的 UV 坐标，推算出“朝向哪里”，就需要一个单位方向向量。*/
}

2. 屏幕点击，找到某个物品。

刚才是将三维空间坐标转换为屏幕坐标，看屏幕里能不能看到。这个就是逆向，也是我们用最多的：用户点击屏幕确定点击的物品。将屏幕上的点击位置映射到立方体贴图（CubeUV）坐标。

现在我们场景里有很多mesh，然后要确认点击的是哪个mesh，以及点击的UV坐标（UV坐标还有一个用法是可以交由上个方法那里添加热点）
1. 屏幕坐标 → NDC 坐标：将像素坐标转换为标准化设备坐标（范围 [-1,1]）
2. 创建射线：从相机位置出发，沿点击方向发射一条射线
3. 检测交点：计算射线与 Mesh 的交点
4. 确定面索引：根据交点所在面确定 faceIndex
5. 计算 UV 坐标：将交点位置转换为面内的 UV 坐标（范围 [0,1]）

/*** 屏幕点击检测场景中的Mesh，并返回点击位置的CubeUV坐标（适用于立方体表面）* @param {THREE.PerspectiveCamera} camera - 当前相机* @param {number} screenX - 屏幕X坐标（像素）* @param {number} screenY - 屏幕Y坐标（像素）* @param {THREE.Object3D[]} meshes - 需要检测的Mesh数组（如场景中的所有可交互物体）* @param {Object} [viewport] - 视口信息 {x, y, width, height}* @returns { { object: THREE.Mesh; cubeUV: CubeUV } | null } - 包含Mesh和CubeUV的对象，或null*/
function screenToMeshCubeUV(camera: THREE.PerspectiveCamera,screenX: number,screenY: number,meshes: THREE.Object3D[],viewport?: Viewport
): { object: THREE.Mesh; cubeUV: CubeUV } | null {// 设置默认视口if (!viewport) {viewport = {width: window.innerWidth,height: window.innerHeight,x: 0,y: 0};}// 1. 屏幕坐标 → NDC坐标（屏幕坐标Y轴向下为正，和canvas相反，所以转换成NDC坐标要反过来）const ndcX = (screenX - viewport.x) / viewport.width * 2 - 1;const ndcY = -(screenY - viewport.y) / viewport.height * 2 + 1; // 翻转Y轴// 2. 创建射线投射器const raycaster = new THREE.Raycaster();raycaster.setFromCamera(new THREE.Vector2(ndcX, ndcY), camera);// 从相机位置出发，沿 NDC 坐标对应的方向发射射线// 3. 检测与所有Mesh的交点（按距离排序，取最近的）const intersects = raycaster.intersectObjects(meshes, true); // true表示检测子对象if (intersects.length === 0) return null;// 获取最近的交点const closestIntersect = intersects[0];const clickedMesh = closestIntersect.object as THREE.Mesh;const point = closestIntersect.point;// 4. 仅处理立方体类型的Mesh（需提前确保Mesh是立方体或平面）if (!(clickedMesh.geometry instanceof THREE.BoxGeometry)) {console.warn('仅支持立方体类型的Mesh');return null;}// 5. 计算CubeUV坐标（假设Mesh是单位立方体，中心在原点）const faceIndex = closestIntersect.face?.index || 0; // face.index是0-5的面索引let u = 0, v = 0;// 立方体每个面的顶点索引规则（Three.js BoxGeometry默认面顺序）// 参考：https://threejs.org/docs/#api/en/geometries/BoxGeometry// 面顺序：右(0)、左(1)、上(2)、下(3)、前(4)、后(5)// 每个面由两个三角形组成，顶点坐标范围[-0.5, 0.5]（假设BoxGeometry未缩放）switch (faceIndex) {case 0: // 右面 (+X)u = 1 - (point.z + 0.5); // z ∈ [-0.5, 0.5] → u ∈ [0, 1]v = 1 - (point.y + 0.5); // y ∈ [-0.5, 0.5] → v ∈ [0, 1]break;case 1: // 左面 (-X)u = (point.z + 0.5);v = 1 - (point.y + 0.5);break;case 2: // 上面 (+Y)u = (point.x + 0.5);v = (point.z + 0.5);break;case 3: // 下面 (-Y)u = (point.x + 0.5);v = 1 - (point.z + 0.5);break;case 4: // 前面 (+Z)u = (point.x + 0.5);v = 1 - (point.y + 0.5);break;case 5: // 后面 (-Z)u = 1 - (point.x + 0.5);v = 1 - (point.y + 0.5);break;default:return null;}// 确保UV在[0,1]范围内（处理浮点精度误差）u = Math.max(0, Math.min(1, u));v = Math.max(0, Math.min(1, v));return {object: clickedMesh,cubeUV: { faceIndex, u, v }};
}

5. 纹理贴图

看这个：https://learnopengl-cn.github.io/01%20Getting%20started/06%20Textures/
但是纹理不能只有纹理贴图，如果想要更加真实，还要设置其他的贴图：

常见的贴图类型包括：

漫反射贴图 (Diffuse Map) - 物体表面的基础颜色和纹理
粗糙度贴图 (Roughness Map) - 控制表面微表面的粗糙程度，影响高光反射的锐利程度。用roughnessMap属性设置。
金属度贴图 (Metallic Map) - 控制表面是金属还是非金属。
法线贴图 (Normal Map) - 通过改变表面法线来模拟表面细节，不改变几何形状。用 normalMap 属性设置。
凹凸贴图（Bump Map） - 模拟表面高低起伏，但效果和法线贴图略有不同，通常用灰度图。用 bumpMap 属性设置。
环境贴图 (Environment Map) - 用于反射和折射的环境图像。用 envMap 属性设置。

在Three.js中，我们可以通过MeshStandardMaterial或MeshPhysicalMaterial来使用这些贴图。

大概像这样：

import * as THREE from 'three';// 贴图加载器
const loader = new THREE.TextureLoader();const colorMap = loader.load('texture/color.jpg');         // 基础色
const roughnessMap = loader.load('texture/roughness.jpg'); // 粗糙度
const normalMap = loader.load('texture/normal.jpg');       // 法线
const bumpMap = loader.load('texture/bump.jpg');           // 凹凸
const envMap = new THREE.CubeTextureLoader().load(['px.jpg', 'nx.jpg', 'py.jpg', 'ny.jpg', 'pz.jpg', 'nz.jpg'
]); // 环境贴图通常是立方体贴图const material = new THREE.MeshStandardMaterial({map: colorMap,roughnessMap: roughnessMap,normalMap: normalMap,bumpMap: bumpMap,envMap: envMap,metalness: 0.5, // 金属度，配合 envMap 更真实roughness: 0.5, // 粗糙度，配合 roughnessMap
});const mesh = new THREE.Mesh(new THREE.BoxGeometry(1, 1, 1),material
);
scene.add(mesh);