目录
Preface
Chapter1 ARM Embedded Systems
1.1 The RISC design philosophy
1.2 The ARM Design Philosophy
1.3 Embedded System Hardware
1.4 Embedded System Software
1.5 Summary
Chapter2 ARM Processor Fundamentals
2.1 Registers
2.2 Current Program Status Register
2.3 Pipeline
2.4 Exceptions, Interrupts, and the Vector Table
2.5 Core Extensions
2.6 Architecture Revisions
2.7 ARM Processor Families
2.8 Summary
Chapter3 Introduction to the ARM Instruction Set
3.1 Data Processing Instructions
3.2 Branch Instructions
3.3 Load-Store Instructions
3.4 Software Interrupt Instruction
3.5 Program Status Register Instructions
3.6 Loading Constants
3.7 ARMv5E Extensions
3.8 Conditional Execution
3.9 Summary
Chapter4 Introduction to the Thumb Instruction Set
4.1 Thumb Register Usage
4.2 ARM-Thumb Interworking
4.3 Other Branch Instructions
4.4 Data Processing Instructions
4.5 Single-Register Load-Store Instructions
4.6 Multiple-Register Load-Store Instructions
4.7 Stack Instructions
4.8 Software Interrupt Instruction
4.9 Summary
Chapter5 Efficient C Programming
5.1 Overview of C Compilers and Optimization
5.2 Basic C Data Types
5.3 C Looping Structures
5.4 Register Allocation
5.5 Function Calls
5.6 Pointer Aliasing
5.7 Structure Arrangement
5.8 Bit-fields
5.9 Unaligned Data and Endianness
5.10 Division
5.11 Floating Point
5.12 Inline Functions and Inline Assembly
5.13 Portability Issues
5.14 Summary
Chapter6 Writing and Optimizing ARM Assembly Code
6.1 Writing Assembly Code
6.2 Profiling and Cycle Counting
6.3 Instruction Scheduling
6.4 Register Allocation
6.5 Conditional Execution
6.6 Looping Constructs
6.7 Bit Manipulation
6.8 Efficient Switches
6.9 Handling Unaligned Data
6.10 Summary
Chapter7 Optimized Primitives
7.1 Double-Precision Integer Multiplication
7.2 Integer Normalization and Count Leading Zeros
7.3 Division
7.4 Square Roots
7.5 Transcendental Functions: log, exp, sin, cos
7.6 Endian Reversal and Bit Operations
7.7 Saturated and Rounded Arithmetic
7.8 Random Number Generation
7.9 Summary
Preface
越来越多的嵌入式系统开发人员和片上系统设计师选择特定的微处理器核心以及一套工具、库和现成组件家族,以便快速开发基于微处理器的新产品。在这个行业中,ARM是一个重要的参与者。过去的10年里,ARM架构已经成为全球最普遍的32位架构,截至目前,全球已经出货超过20亿个基于ARM的处理器。ARM处理器被嵌入到从手机到汽车制动系统等各种产品中。在半导体和产品设计公司中,建立了一个全球性的ARM合作伙伴和第三方供应商社区,包括硬件工程师、系统设计师和软件开发人员。然而,迄今为止还没有一本书直接满足他们在ARM嵌入式设计方面系统和软件开发的需求。本书填补了这一空白。
我们的目标是从产品开发者的角度描述ARM核心的操作,特别强调软件部分。因为我们专门为有嵌入式系统开发经验但可能对ARM架构不熟悉的工程师编写了本书,所以我们假设读者没有之前的ARM经验。
为了帮助读者尽快提高生产力,我们提供了一套ARM软件示例,可以集成到商业产品中,或作为快速创建生产力软件的模板。这些示例有编号,以便读者可以轻松地在出版商的网站上找到源代码。这些示例对于有ARM设计经验并希望最高效利用基于ARM的嵌入式系统的人也非常有价值。
Organization of the Book
本书首先简要介绍了ARM处理器设计理念,并讨论了它与传统RISC理念的区别及原因。第一章还介绍了一个基于ARM处理器的简单嵌入式系统。
第二章更深入地讨论了硬件,聚焦于ARM处理器核心,并概述了当前市场上的ARM核心。
第三章和第四章分别侧重于ARM和Thumb指令集,并构成本书其余内容的基础。重点指令的解释包括完整示例,因此这两章也可以作为指令集教程。
第五章和第六章展示了如何编写高效的代码,并提供了大量我们在与ARM客户合作时开发的示例。第五章教授编写能够在ARM架构上高效编译的C代码的经验技巧和规则,并帮助确定哪些代码应进行优化。第六章详细介绍了编写和优化ARM汇编代码的最佳实践,这对于通过降低系统功耗和时钟速度来提高性能至关重要。
原语是广泛应用于各种算法的基本操作,了解如何优化它们非常有价值。第七章讨论了如何针对特定的ARM处理器优化原语。它提供了经过优化的常见原语的参考实现,以及更复杂的数学运算的参考实现,以供快速参考。对于那些希望深入了解每个实现背后的理论的人,我们还包括了相关理论。
音频和视频嵌入式系统应用需求越来越高。它们需要数字信号处理(DSP)能力,而以前通常需要单独的DSP处理器来提供此功能。然而,现在ARM架构提供了更高的内存带宽和更快的乘-累加操作,使得单个ARM核心设计能够支持这些应用。第八章探讨了如何最大化ARM在数字处理应用中的性能,并介绍了如何实现DSP算法。
嵌入式系统的核心是异常处理程序。高效的处理程序可以显著提高系统性能。第九章通过一系列详细示例,介绍了在ARM处理器上处理异常和中断的理论和实践。
固件是任何嵌入式系统的重要组成部分,在第十章中,我们通过一个称为Sandstone的简单固件包来描述。该章还回顾了可用于ARM的流行行业固件包。
第十一章通过我们设计的一个示例操作系统(Simple Little Operating System)演示了嵌入式操作系统的实现。
第十二、十三和十四章侧重于存储器问题。第十二章讨论围绕ARM核心的各种缓存技术,演示了控制特定支持缓存的ARM处理器上缓存的例程。第十三章讨论了内存保护单元,而第十四章讨论了内存管理单元。
最后,在第十五章中,我们考虑了ARM架构的未来,重点介绍了指令集的新方向和ARM在未来几年内正在实施的新技术。
附录提供了有关指令集、周期计时和具体ARM产品的详细参考信息。
Chapter1 ARM Embedded Systems
ARM处理器内核是许多成功的32位嵌入式系统的关键组件。您可能自己就拥有其中之一,甚至可能没有意识到!ARM内核广泛应用于手机、手持组织器和其他许多日常便携消费设备中。
从1985年的第一款ARM1原型机起,ARM的设计师们已经取得了长足的进步。到2001年底,全球已经发货超过十亿个ARM处理器。ARM公司的成功基于一个简单而强大的原始设计,通过不断的技术创新,至今仍在不断改进。实际上,ARM内核不是单一的内核,而是一个共享相似设计原则和共同指令集的整个系列设计。
例如,ARM最成功的内核之一是ARM7TDMI。它提供高达120 Dhrystone MIPS1的性能,并以其高代码密度和低功耗而闻名,非常适合移动嵌入式设备。
在这第一章中,我们将讨论RISC(精简指令集计算机)设计理念如何被ARM采用来创建一种灵活的嵌入式处理器。然后,我们介绍一个示例嵌入式设备,并讨论围绕ARM处理器的典型硬件和软件技术。
1.1 The RISC design philosophy
ARM内核采用了RISC体系结构。RISC是一种设计理念,旨在提供在高时钟速度下在单个周期内执行的简单但强大的指令。RISC哲学注重降低硬件执行的指令复杂性,因为在软件中提供更大的灵活性和智能化比在硬件中更容易实现。因此,RISC设计对编译器提出了更高的要求。
相比之下,传统的复杂指令集计算机(CISC)更多地依赖于硬件来提供指令功能,因此CISC指令更加复杂。图1.1展示了这些主要区别。

RISC哲学通过四条主要设计规则来实现:
1. 指令:RISC处理器具有减少的指令类别。这些类别提供简单的操作,每个操作可以在一个周期内执行。编译器或程序员通过组合多个简单指令来合成复杂的操作(例如除法操作)。每个指令都是固定长度的,以允许流水线在解码当前指令之前获取未来的指令。相比之下,CISC处理器的指令往往具有可变大小,并需要多个周期来执行。
2. 流水线:指令的处理被分解为可以由流水线并行执行的较小单元。理想情况下,流水线每个周期推进一步,以实现最大吞吐量。指令可以在流水线阶段中进行解码。不需要像CISC处理器那样通过称为微码的小程序执行指令。
3. 寄存器:RISC机器具有大型通用寄存器集。任何寄存器都可以包含数据或地址。寄存器充当所有数据处理操作的快速本地存储器。相比之下,CISC处理器具有用于特定目的的专用寄存器。
4. 载入-存储架构:处理器对寄存器中保存的数据进行操作。独立的载入和存储指令在寄存器组和外部存储器之间传输数据。存储器访问是昂贵的,因此将内存访问与数据处理分离提供了一个优势,因为您可以在不需要多次内存访问的情况下多次使用寄存器组中保存的数据项。相比之下,CISC设计可以直接对内存进行数据处理操作。
这些设计规则使得RISC处理器更简单,因此核心可以以更高的时钟频率运行。相比之下,传统的CISC处理器更复杂,时钟频率较低。然而,在过去的二十年里,RISC和CISC之间的区别已经模糊,因为CISC处理器已经实现了更多的RISC概念。
1.2 The ARM Design Philosophy
ARM处理器的设计受到了许多物理特性的驱动。首先,便携式嵌入式系统需要某种形式的电池供电。ARM处理器经过专门设计,体积小以减少功耗并延长电池运行时间,这对于移动电话和个人数字助理(PDA)等应用至关重要。
高代码密度是另一个主要需求,因为由于成本和/或物理尺寸限制,嵌入式系统具有有限的内存。高代码密度对于具有有限板载内存的应用非常有用,例如移动电话和大容量存储设备。
此外,嵌入式系统对价格敏感,并使用速度较慢且低成本的存储设备。对于像数码相机这样的大规模应用,每一美分在设计中都必须考虑到。能够使用低成本的存储设备可以节省大量费用。
另一个重要需求是减少嵌入式处理器占据的芯片面积。对于单芯片解决方案,嵌入式处理器占用的面积越小,专用外设的可用空间就越多。这反过来降低了设计和制造的成本,因为终端产品所需的离散芯片更少。
ARM在处理器内部集成了硬件调试技术,使软件工程师可以在处理器执行代码时查看发生的情况。有了更大的可视性,软件工程师可以更快地解决问题,这直接影响上市时间并降低总体开发成本。
ARM核心并不是纯粹的RISC架构,因为它主要应用于嵌入式系统的限制。在某种意义上,ARM核心的优势在于它没有将RISC概念推得太远。在当今的系统中,关键不是原始处理器速度,而是总体有效的系统性能和功耗。
1.2.1 Instruction Set for Embedded Systems
ARM指令集与纯粹的RISC定义有几个不同之处,使得ARM指令集适用于嵌入式应用:
■ 对于某些指令,可变周期执行-并非每个ARM指令都在一个周期内执行。例如,加载-存储-多数据指令的执行周期数取决于传输的寄存器数量。传输可以在连续的内存地址上进行,这提高了性能,因为顺序内存访问通常比随机访问更快。代码密度也得到提高,因为多个寄存器传输是函数开头和结尾常见的操作。
■ 内联移位器导致更复杂的指令-内联移位器是一种硬件组件,在指令使用之前对其中一个输入寄存器进行预处理。这扩展了许多指令的功能,提高了核心性能和代码密度。我们会在第2、3和4章中详细解释这个特性。
■ Thumb 16位指令集-ARM通过添加第二个16位指令集Thumb来增强处理器核心,允许ARM核心执行16位或32位指令。与32位固定长度指令相比,16位指令可以将代码密度提高约30%。
■ 条件执行-只有在满足特定条件时才执行指令。这个特性通过减少分支指令提高了性能和代码密度。
■ 增强指令-增强型数字信号处理器(DSP)指令被添加到标准ARM指令集中,以支持快速16×16位乘法运算和饱和运算。这些指令允许在某些情况下,更高性能的ARM处理器替代传统的处理器加DSP的组合。
这些额外的特性使得ARM处理器成为最常用的32位嵌入式处理器核心之一。全球许多顶级半导体公司都生产基于ARM处理器的产品。
1.3 Embedded System Hardware
嵌入式系统可以控制许多不同的设备,从生产线上发现的小型传感器到NASA太空探测器上使用的实时控制系统。所有这些设备都使用软件和硬件组件的组合。每个组件都被选择为高效,并且如果适用,设计用于未来的扩展和扩展。

图1.2显示了一个基于ARM核心的典型嵌入式设备。每个方框代表一个特性或功能。连接方框的线是传输数据的总线。我们可以将该设备分为四个主要的硬件组件:
■ ARM处理器控制嵌入式设备。根据所需的操作特性,可使用不同版本的ARM处理器。ARM处理器包括一个核心(执行引擎,处理指令并操作数据)以及与总线进行接口连接的周围组件。这些组件可以包括内存管理和缓存。
■ 控制器协调系统中重要的功能模块。常见的两个控制器是中断控制器和存储器控制器。
■ 外围设备提供芯片外部的所有输入输出能力,并负责嵌入式设备的特色功能。
■ 总线用于在设备的不同部分之间进行通信。
1.3.1 ARM Bus Technology
嵌入式系统使用与设计用于x86个人计算机的总线技术不同的总线技术。最常见的个人计算机总线技术是外围组件互连(PCI)总线,它连接诸如显卡和硬盘控制器之类的设备到x86处理器总线上。这种类型的技术是外部或片外的(即总线设计用于与芯片外部的设备进行机械和电气连接),并集成在个人计算机的主板中。
相反,嵌入式设备使用内部总线,该总线是芯片内部的,并允许不同的外围设备与ARM核心互连。
总线上连接的设备分为两个不同的类别。ARM处理器核心是总线主控,是一个逻辑设备,能够在同一总线上与另一个设备发起数据传输。外围设备则往往是总线从设备,只能对来自总线主控设备的传输请求做出响应。
总线具有两个层次的架构。第一层是物理层,涵盖电气特性和总线宽度(16、32或64位)。第二层处理协议,即处理器与外围设备之间通信的逻辑规则。
ARM主要是一个设计公司。它很少实现总线的电气特性,但经常指定总线协议。
1.3.2 AMBA Bus Protocol
1996年引入了先进的单片机总线结构(AMBA),并广泛被采用作为用于ARM处理器的片上总线架构。最早引入的AMBA总线是ARM系统总线(ASB)和ARM外围总线(APB)。后来ARM又引入了另一种总线设计,称为ARM高性能总线(AHB)。使用AMBA,外围设备设计者可以在多个项目中重复使用相同的设计。由于有大量使用AMBA接口开发的外围设备,硬件设计师在设备中可选择经过测试和验证的外围设备。
外围设备可以简单地连接到片上总线上,而无需为每种不同的处理器架构重新设计接口。这种面向硬件开发人员的即插即用接口提高了可用性和上市时间。
AHB提供的数据吞吐量比ASB更高,因为它基于集中式多路复用总线方案,而不是ASB的双向总线设计。这种改变使得AHB总线能够以更高的时钟速度运行,并且是第一个支持64位和128位宽度的ARM总线。ARM引入了两种AHB总线的变体:多层AHB和AHB-Lite。与原始的AHB总线允许任何时候只有一个总线主控处于活动状态不同,多层AHB总线允许多个总线主控处于活动状态。AHB-Lite是AHB总线的子集,仅限于一个总线主控。该总线适用于不需要标准AHB总线的全部功能的设计。
AHB和多层AHB支持相同的主从协议,但具有不同的互连方式。多层AHB中的新互连方式适用于具有多个处理器的系统。它们允许并行操作,并提供更高的吞吐率。
图1.2中显示的示例设备有三个总线:用于高性能外围设备的AHB总线,用于较慢外围设备的APB总线,以及专有的第三个外部外围设备总线。此外,该外部总线需要一个专门的桥接器与AHB总线连接起来。
1.3.3 Memory
嵌入式系统必须拥有某种形式的存储器来存储和执行代码。在确定特定的存储器特性时,例如层次结构、宽度和类型,您需要比较价格、性能和功耗。如果为了保持所需带宽而使存储器运行速度加倍,那么存储器的功耗要求可能会更高。
1.3.3.1 Hierarchy
所有计算机系统都以某种形式的层次结构安排了存储器。图1.2显示了支持外部片上存储器的设备。处理器内部有一个缓存选项(图1.2中未显示)来提高存储器性能。

图1.3展示了存储器的权衡:最快的缓存位于ARM处理器核心附近,最慢的二级存储远离核心。一般来说,离处理器核心越近的存储器成本越高,容量越小。
缓存位于主存和处理器核心之间。它用于加快处理器与主存之间的数据传输。缓存可以提高总体性能,但会损失可预测的执行时间。尽管缓存提高了系统的一般性能,但对于实时系统响应并没有帮助。需要注意的是,许多小型嵌入式系统不需要缓存的性能优势。
主存储器较大,大约为256 KB到256 MB(甚至更大),根据应用程序的不同而异,并通常存储在单独的芯片中。加载和存储指令访问主存储器,除非这些值已存储在缓存中以进行快速访问。二级存储是容量最大、速度最慢的存储形式。硬盘驱动器和CD-ROM驱动器是二级存储的示例。现在的二级存储容量可以从600 MB到60 GB不等。
1.3.3.2 Width
存储器宽度是每次访问存储器返回的位数,通常为8、16、32或64位。存储器宽度直接影响整体性能和成本比。
如果您使用32位ARM指令和16位宽存储芯片的非缓存系统,则处理器每条指令需要进行两次存储器获取。每次获取需要两次16位加载。显然,这会降低系统性能,但好处是16位存储器成本较低。
相反,如果核心执行16位Thumb指令,使用16位存储器将获得更好的性能。较高的性能是因为核心只需进行一次存储器取指操作来加载指令。因此,使用16位宽存储器设备的Thumb指令提供了改进的性能和降低的成本。
表1.1总结了在使用不同存储器宽度设备的ARM处理器上的理论周期时间。

1.3.3.3 Types
有许多不同类型的存储器。在这一部分,我们介绍一些在基于ARM的嵌入式系统中常见的存储器设备。
只读存储器(ROM)是所有存储器类型中最不灵活的,因为它包含的映像在生产时被永久设置,并且无法重新编程。ROM通常用于不需要更新或更正的大批量设备。许多设备还使用ROM来保存引导代码。
闪存ROM可以进行写入和读取操作,但写入速度较慢,因此不应将其用于保存动态数据。它主要用于保存设备固件或在断电后需要保留的长期数据。闪存ROM的擦除和编程完全由软件控制,无需额外的硬件电路,从而降低了制造成本。闪存ROM已成为最流行的只读存储器类型之一,并且目前被用作大规模或二级存储的替代方案。
动态随机存取存储器(DRAM)是设备中最常用的RAM类型。与其他RAM类型相比,它的每兆字节成本最低。DRAM是动态的,它需要定期刷新存储单元并提供新的电荷,因此在使用存储器之前需要设置DRAM控制器。
静态随机存取存储器(SRAM)比传统的DRAM更快,但需要更多的硅片面积。SRAM是静态的,不需要刷新存储器。SRAM的访问时间比等效的DRAM短得多,因为SRAM在数据访问之间不需要暂停。由于成本较高,它主要用于较小的高速任务,如快速存储器和缓存。
同步动态随机存取存储器(SDRAM)是DRAM的许多子类别之一。它可以以比传统存储器更高的时钟速度运行。SDRAM与处理器总线进行同步,因为它是时钟同步的。在内部,数据从存储单元中获取、流水线处理,最后以突发方式传输到总线上。老式的异步DRAM的突发效率不如SDRAM高。
1.3.4 Peripherals
与外部世界交互的嵌入式系统需要某种形式的外设设备。外设设备通过连接到芯片之外的其他设备或传感器,在芯片上执行输入和输出功能。每个外设设备通常执行单个功能,并且可以位于芯片上。外设设备的范围从简单的串行通信设备到更复杂的802.11无线设备不等。
所有ARM外设都是内存映射的,即编程接口是一组内存寻址的寄存器。这些寄存器的地址是相对于特定外设基地址的偏移量。
控制器是在嵌入式系统中实现更高级功能的专用外设。两种重要类型的控制器是内存控制器和中断控制器。
1.3.4.1 Memory Controllers
内存控制器将不同类型的存储器连接到处理器总线。在上电时,硬件会配置一个内存控制器,以允许特定的存储器设备处于活动状态。这些存储器设备允许执行初始化代码。有些存储器设备必须由软件进行设置;例如,在使用DRAM时,您首先必须设置内存的时序和刷新频率,然后才能访问它。
1.3.4.2 Interrupt Controllers
当外设或设备需要处理时,它会向处理器发出中断。中断控制器提供了可编程的管理策略,允许软件确定在任何特定时间哪个外设或设备可以中断处理器,通过在中断控制器寄存器中设置适当的位来实现。
ARM处理器有两种类型的中断控制器:标准中断控制器和向量中断控制器(VIC)。
标准中断控制器在外部设备请求服务时向处理器核心发送中断信号。它可以被编程为忽略或屏蔽单个设备或一组设备。中断处理程序通过读取中断控制器中的设备位图寄存器来确定哪个设备需要服务。
VIC比标准中断控制器更强大,因为它对中断进行优先级排序,并简化了确定引发中断的设备的过程。在为每个中断关联了优先级和处理程序地址后,只有当新中断的优先级高于当前执行的中断处理程序时,VIC才向核心发出中断信号。根据其类型,VIC要么调用标准中断异常处理程序(可以从VIC加载设备处理程序的地址),要么直接使核心跳转到设备的处理程序。
1.4 Embedded System Software
嵌入式系统需要软件来驱动。图1.4显示了控制嵌入式设备所需的四个典型软件组件。软件堆栈中的每个组件使用更高层次的抽象来将代码与硬件设备分离。

初始化代码是在板上执行的第一个代码,它针对特定的目标或一组目标。它在将控制权交给操作系统之前设置了板上的最小部件。
操作系统提供了一个基础架构来控制应用程序和管理硬件系统资源。许多嵌入式系统不需要完整的操作系统,只需要一个简单的任务调度器,可以是事件驱动或轮询驱动。
设备驱动程序是图1.4中显示的第三个组件。它们为硬件设备上的外设提供了一致的软件接口。
最后,应用程序执行设备所需的任务之一。例如,手机可能有一个日记应用程序。可能会有多个应用程序在同一设备上运行,并由操作系统进行控制。
这些软件组件可以从ROM或RAM中运行。固定在设备上的ROM代码(例如初始化代码)称为固件。
1.4.1 Initialization (Boot) Code
初始化代码(或引导代码)将处理器从复位状态转换到操作系统可以运行的状态。它通常配置内存控制器和处理器缓存,并初始化一些设备。在简单系统中,操作系统可以被简单的调度器或调试监视器所替代。
初始化代码在将控制权交给操作系统镜像之前处理一些任务。我们可以将这些不同的任务分为三个阶段:初始硬件配置、诊断和引导。
初始硬件配置涉及设置目标平台,使其能够引导镜像。尽管目标平台本身以标准配置启动,但此配置通常需要修改以满足引导镜像的要求。例如,内存系统通常需要重新组织内存映射,如示例1.1所示。
诊断通常嵌入在初始化代码中。诊断代码通过对硬件目标进行测试来检查目标是否正常工作。它还追踪标准的与系统相关的问题。这种类型的测试对于制造业来说非常重要,因为它发生在软件产品完成之后。诊断代码的主要目的是故障识别和隔离。
引导涉及加载一个镜像并将控制权交给该镜像。如果系统必须引导不同的操作系统或同一操作系统的不同版本,则引导过程本身可能很复杂。
加载镜像是最后一个阶段,但首先必须加载镜像。加载镜像可以包括将整个程序(包括代码和数据)复制到RAM中,也可以只复制包含易失性变量的数据区域到RAM中。引导完成后,系统通过修改程序计数器指向镜像的起始位置来交出控制权。
有时为了减小镜像的大小,镜像会被压缩。然后在加载镜像或将控制权交给镜像时进行解压缩。
示例1.1
初始化或组织内存是初始化代码的重要部分,因为许多操作系统在启动之前需要一个已知的内存布局。
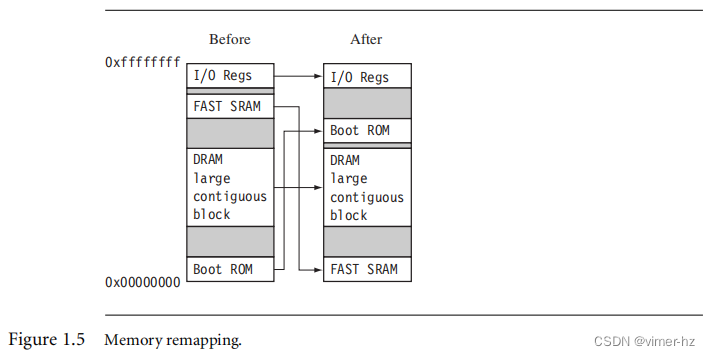
图1.5显示了重新组织前后的内存情况。基于ARM的嵌入式系统通常提供内存重映射功能,因为它允许系统在上电时从ROM中启动初始化代码。然后,初始化代码重新定义或重映射内存映射,将RAM放置在地址0x00000000处——这是一个重要的步骤,因为异常向量表可以位于RAM中,从而可以重新编程。我们将在第2.4节中更详细地讨论向量表。
1.4.2 Operating System
初始化过程准备硬件以供操作系统接管控制。操作系统组织系统资源:外设、内存和处理时间。通过操作系统控制这些资源,它们可以被在操作系统环境中运行的不同应用程序高效利用。
ARM处理器支持50多个操作系统。我们可以将操作系统分为两个主要类别:实时操作系统(RTOS)和平台操作系统。
RTOS提供对事件的保证响应时间。不同的操作系统对系统响应时间有不同程度的控制。硬实时应用程序需要保证的响应时间才能正常工作。相比之下,软实时应用程序需要较好的响应时间,但如果响应时间超过限制,性能会更加平稳地下降。运行RTOS的系统通常没有辅助存储。
平台操作系统需要一个内存管理单元来管理大型的非实时应用程序,并且往往具有辅助存储。Linux操作系统是平台操作系统的典型例子。
这两类操作系统并不互斥:有些操作系统使用带有内存管理单元的ARM核心,并具有实时特性。ARM开发了一组专门针对每个类别的处理器核心。
1.4.3 Applications
操作系统调度应用程序,这些应用程序是专门用于处理特定任务的代码。一个应用程序实现一个处理任务;操作系统控制环境。嵌入式系统可以只有一个活动应用程序,也可以同时运行多个应用程序。
ARM处理器广泛应用于众多市场领域,包括网络、汽车、移动和消费设备、大容量存储和成像。在每个领域中,ARM处理器可以应用于多个应用领域。
例如,ARM处理器应用于网络应用,如家庭网关、用于高速互联网通信的DSL调制解调器和802.11无线通信。移动设备领域是ARM处理器最大的应用领域,因为有移动电话的存在。ARM处理器也被应用于大容量存储设备,如硬盘,以及成像产品,如喷墨打印机——这些应用要求成本敏感且产量大。
相比之下,ARM处理器不适用于需要领先高性能的应用。因为这些应用往往产量低且成本高,ARM决定不将设计重点放在这些类型的应用上。
1.5 Summary
ARM使用了修改过的RISC设计理念,旨在提高代码密度和降低功耗,而不仅仅追求高性能。嵌入式系统由处理器核心、缓存、内存和外设组成,并由操作系统软件控制管理应用任务。
RISC设计理念的关键点包括通过简化指令的复杂性来提高性能,通过使用流水线来加快指令处理速度,提供一个大的寄存器集以将数据存储在核心附近,并使用加载存储结构。ARM的设计理念还融合了一些非RISC的想法:
- 它允许某些指令的可变周期执行,以节省功耗、面积和代码大小。
- 它添加了一个位移器来扩展某些指令的功能。
- 它使用Thumb 16位指令集来提高代码密度。
- 它通过条件执行指令来提高代码密度和性能。
- 它包含增强型指令来执行数字信号处理类型的功能。
嵌入式系统包括以下硬件组件:ARM处理器嵌入在芯片中。程序员通过内存映射寄存器访问外设。还有一种特殊类型的外设称为控制器,嵌入式系统使用它来配置更高级别的功能,如内存和中断。AMBA片上总线用于连接处理器和外设。
嵌入式系统还包括以下软件组件:初始化代码将硬件配置为已知状态。一旦配置完成,可以加载和执行操作系统。操作系统为使用硬件资源和基础设施提供了一个共同的编程环境。设备驱动程序提供了与外设的标准接口。应用程序执行嵌入式系统的特定任务职责。
Chapter2 ARM Processor Fundamentals
第1章介绍了带有ARM处理器的嵌入式系统。在本章中,我们将重点介绍处理器本身。首先,我们将概述处理器核心,并描述数据在不同部分之间的传输方式。我们将从软件开发者的角度描述ARM处理器的程序员模型,展示处理器核心的功能以及不同部分的相互作用。我们还将查看构成ARM处理器的核心扩展。核心扩展加速和组织主存,并扩展指令集。然后,我们将描述ARM核心体系结构的修订,包括用于标识它们的ARM核心命名规则以及ARM指令集体系结构的时间顺序变化。最后一节介绍了架构实现,将它们分为具体的ARM处理器核心系列。

程序员可以将ARM核心视为由数据总线连接的功能单元,如图2.1所示,箭头表示数据流动,线条表示总线,方框表示操作单元或存储区域。该图不仅显示了数据流动,还显示了构成ARM核心的抽象组件。
数据通过数据总线进入处理器核心。这些数据可能是要执行的指令或数据项。图2.1显示了ARM的冯·诺伊曼实现,数据项和指令共享同一总线。相比之下,哈佛实现的ARM使用两个不同的总线。
指令解码器在执行之前对指令进行翻译。每条执行的指令都属于特定的指令集。
ARM处理器和所有RISC处理器一样,采用加载-存储体系结构。这意味着它具有两种指令类型,用于在处理器内部传输数据:加载指令将数据从内存复制到核心中的寄存器,而存储指令则将数据从寄存器复制到内存。没有直接操作内存中数据的数据处理指令。因此,数据处理完全在寄存器中进行。
数据项存放在寄存器文件中,这是一个由32位寄存器构成的存储区。由于ARM核心是一个32位处理器,大多数指令将寄存器视为保存有符号或无符号32位值的容器。符号扩展硬件在将有符号8位和16位数从内存读取并放入寄存器时,将其转换为32位值。
ARM指令通常有两个源寄存器Rn和Rm,一个结果寄存器或目的寄存器Rd。源操作数分别通过内部总线A和B从寄存器文件中读取。
算术逻辑单元(ALU)或乘累加单元(MAC)从A和B总线中获取寄存器值Rn和Rm,并计算出一个结果。数据处理指令直接将结果写入Rd寄存器文件。加载和存储指令使用ALU生成一个地址,并将其保存在地址寄存器中,并通过地址总线广播。
ARM的一个重要特性是寄存器Rm可以在进入ALU之前经过移位器进行预处理。移位器和ALU共同可以计算广泛的表达式和地址。
经过功能单元后,Rd中的结果通过结果总线写回到寄存器文件中。对于加载和存储指令,增量器在核心从下一个顺序内存位置读取或写入下一个寄存器值之前更新地址寄存器。处理器将继续执行指令,直到异常或中断改变正常的执行流程。
现在您已经对处理器核心有了概述,我们将更详细地查看处理器的一些关键组件:寄存器、当前程序状态寄存器(cpsr)和流水线。
2.1 Registers
通用寄存器可以保存数据或地址。它们以字母r作为寄存器编号的前缀进行标识。例如,寄存器4被标记为r4。图2.2显示了在用户模式下(通常在执行应用程序时使用的受保护模式)可用的活动寄存器。处理器可以在七个不同的模式下运行,我们将很快介绍这些模式。所有显示的寄存器大小均为32位。
最多有18个活动寄存器:16个数据寄存器和2个处理器状态寄存器。对于程序员来说,数据寄存器可视为r0到r15。
ARM处理器有三个寄存器分配给特定任务或特殊功能:r13、r14和r15。它们经常被赋予不同的标签以区分它们与其他寄存器。

在图2.2中,阴影寄存器标识了被分配给特殊用途的寄存器:
- 寄存器r13传统上用作堆栈指针(sp),并存储当前处理器模式下堆栈的首地址。
- 寄存器r14称为链接寄存器(lr),每当核心调用子程序时,会将返回地址放在该寄存器中。
- 寄存器r15是程序计数器(pc),包含处理器要获取的下一条指令的地址。
根据上下文,寄存器r13和r14也可以用作通用寄存器,在处理器模式更改期间可以选择使用这些寄存器,这可能特别有用。然而,在处理器运行任何形式的操作系统时,使用r13作为通用寄存器是危险的,因为操作系统通常假定r13始终指向有效的堆栈帧。
在ARM状态下,寄存器r0到r13是正交的,即适用于r0的任何指令同样适用于其他所有寄存器。但是,有一些指令以特殊方式处理r14和r15。
除了16个数据寄存器外,还有两个程序状态寄存器:cpsr(当前程序状态寄存器)和spsr(保存的程序状态寄存器)。
寄存器文件包含了程序员可用的所有寄存器。程序员可见的寄存器取决于处理器的当前模式。
2.2 Current Program Status Register
ARM核心使用cpsr来监控和控制内部操作。cpsr是一个专用的32位寄存器,位于寄存器文件中。图2.3显示了通用程序状态寄存器的基本布局。请注意,阴影部分保留供将来扩展使用。

cpsr被分成四个字段,每个字段宽度为8位:标志位(flags)、状态位(status)、扩展位(extension)和控制位(control)。在当前设计中,扩展字段和状态字段保留供将来使用。控制字段包含处理器模式、状态和中断屏蔽位。标志字段包含条件标志。
一些ARM处理器核心分配了额外的位。例如,J位可以在标志字段中找到,仅在启用Jazelle的处理器上可用,该处理器执行8位指令。我们将在第2.2.3节中更详细地讨论Jazelle。未来的设计很有可能分配额外的位来监控和控制新功能。
有关cpsr的完整描述,请参考附录B。
2.2.1 Processor Modes
处理器模式确定哪些寄存器处于活动状态以及对cpsr寄存器本身的访问权限。每个处理器模式都可以是特权模式或非特权模式:特权模式允许对cpsr进行完全的读写访问,而非特权模式只允许对cpsr中的控制字段进行读取访问,但仍允许对条件标志进行读写访问。
总共有七种处理器模式:六种特权模式(中止模式、快速中断请求模式、中断请求模式、监管者模式、系统模式和未定义模式)和一种非特权模式(用户模式)。
当出现访问内存失败的情况时,处理器进入中止模式。快速中断请求模式和中断请求模式对应于ARM处理器上可用的两个中断级别。监管者模式是处理器在复位后所处的模式,通常是操作系统内核运行的模式。系统模式是用户模式的一个特殊版本,允许对cpsr进行完全的读写访问。当处理器遇到未定义或不受实现支持的指令时,会使用未定义模式。用户模式用于程序和应用程序。
2.2.2 Banked Registers
图2.4显示了寄存器文件中的所有37个寄存器。其中,有20个寄存器在不同时间对程序隐藏。这些寄存器被称为分段寄存器,并且在图示中用阴影标识出来。它们仅在处理器处于特定模式时可用;例如,中止模式具有分段寄存器r13_abt、r14_abt和spsr_abt。特定模式的分段寄存器由附加在模式助记符或_mode后面的下划线字符表示。

除了用户模式外,每种处理器模式都可以通过直接向cpsr的模式位写入来更改模式。除系统模式外的所有处理器模式都有一组关联的分段寄存器,它们是主要的16个寄存器的子集。分段寄存器与用户模式寄存器一一对应。如果更改处理器模式,来自新模式的分段寄存器将替换现有的寄存器。
例如,当处理器处于中断请求模式时,您执行的指令仍然访问名为r13和r14的寄存器。然而,这些寄存器是分段寄存器r13_irq和r14_irq。用户模式寄存器r13_usr和r14_usr不受引用这些寄存器的指令的影响。程序仍然可以正常访问其他寄存器r0到r12。
可以通过编写直接到cpsr的程序(处理器核心必须处于特权模式)或由硬件在核心响应异常或中断时更改处理器模式。以下异常和中断会导致模式更改:复位、中断请求、快速中断请求、软中断、数据中止、预取中止和未定义指令。异常和中断会暂停顺序指令的正常执行,并跳转到特定位置。
图2.5说明了当中断强制进行模式更改时发生的情况。该图显示了核心从用户模式更改为中断请求模式,这在外部设备向处理器核心引发中断时发生。此更改会导致用户寄存器r13和r14被分段。用户寄存器分别被r13_irq和r14_irq寄存器替换。请注意,r14_irq包含返回地址,r13_irq包含中断请求模式的堆栈指针。

图2.5还显示了中断请求模式中出现的新寄存器:保存的程序状态寄存器(spsr),用于存储前一个模式的cpsr。您可以在图示中看到cpsr被复制到spsr_irq。要返回到用户模式,使用特殊的返回指令,指示核心从spsr_irq还原原始的cpsr,并将用户寄存器r13和r14分段。请注意,spsr只能在特权模式下进行修改和读取,在用户模式下不可用。
还要注意的另一个重要特点是,当程序直接向cpsr写入以强制进行模式更改时,cpsr不会被复制到spsr中。只有在发生异常或中断时才会保存cpsr。
图2.3显示当前活动处理器模式占用cpsr的最低有效位的五个位。当给核心供电时,它启动于特权模式(supervisor mode),这是一种特权模式。从特权模式开始很有用,因为初始化代码可以使用完全访问cpsr来设置每个其他模式的栈。

表2.1列出了各种模式及其关联的二进制模式。表的最后一列给出了表示cpsr中每个处理器模式的位模式。
2.2.3 State and Instruction Sets
核心的状态确定正在执行哪个指令集。有三种指令集:ARM、Thumb和Jazelle。只有处理器处于ARM状态时,ARM指令集才处于活动状态。同样地,只有处理器处于Thumb状态时,Thumb指令集才处于活动状态。一旦处于Thumb状态,处理器就会纯粹地执行Thumb 16位指令。不能混合使用顺序的ARM、Thumb和Jazelle指令。
cpsr中的Jazelle J和Thumb T位反映了处理器的状态。当J和T位均为0时,处理器处于ARM状态并执行ARM指令。这是处理器上电时的情况。当T位为1时,处理器处于Thumb状态。要更改状态,核心执行一个专门的分支指令。表2.2对比了ARM和Thumb指令集的特性。

ARM设计者引入了第三个指令集,称为Jazelle。Jazelle执行8位指令,是一种软硬混合设计,旨在加速执行Java字节码。
要执行Java字节码,您需要Jazelle技术以及经过特别修改的Java虚拟机版本。需要注意的是,Jazelle的硬件部分仅支持Java字节码的子集;其余部分在软件中模拟执行。Jazelle指令集是一种封闭的指令集,不对外公开。表2.3列出了Jazelle指令集的特点。

2.2.4 Interrupt Masks
中断屏蔽用于阻止特定的中断请求打断处理器的执行。ARM处理器核心提供了两个中断请求级别:中断请求(IRQ)和快速中断请求(FIQ)。
cpsr寄存器有两个中断屏蔽位,即第7位和第6位(或称为I位和F位),分别用于控制IRQ和FIQ的屏蔽。当I位设置为二进制1时,屏蔽IRQ;类似地,当F位设置为二进制1时,屏蔽FIQ。
2.2.5 Condition Flags
条件标志位通过比较和指定S指令后缀的ALU操作进行更新。例如,如果SUBS减法指令结果导致寄存器的值为零,则cpsr中的Z标志位将被设置。这个特定的减法指令会明确地更新cpsr。
对于包含DSP扩展的处理器核心,Q位指示增强型DSP指令是否发生了溢出或饱和。该标志位是“粘性”的,意味着只有硬件会设置该标志位。要清除该标志位,需要直接向cpsr写入数据。
在启用Jazelle的处理器中,J位反映了核心的状态;如果设置了该位,表示核心处于Jazelle状态。通常情况下,J位不可用,仅在某些处理器核心上可用。要利用Jazelle,还需要从ARM Limited和Sun Microsystems获取额外的软件授权。

大多数ARM指令可以根据条件标志位的值进行有条件执行。表2.4列出了条件标志位及其被设置的原因的简要描述。这些标志位位于cpsr的最高有效位。这些位用于条件执行。

图2.6显示了具有DSP扩展和Jazelle的cpsr的典型值。本书使用一种更易读的记法来表示cpsr的数据。当一个位为二进制1时,我们使用大写字母;当一个位为二进制0时,我们使用小写字母。对于条件标志位,大写字母表示该标志已被设置。对于中断,大写字母表示中断被禁用。
在图2.6中显示的cpsr示例中,只有C标志位被设置。其余的nzvq标志位都被清除。处理器处于ARM状态,因为既没有设置Jazelle j位,也没有设置Thumb t位。IRQ中断被启用,FIQ中断被禁用。最后,从图中可以看出,处理器处于特权(SVC)模式,因为mode[4:0]等于二进制10011。
2.2.6 Conditional Execution
条件执行控制处理器是否执行指令。大多数指令都有一个条件属性,该属性根据条件标志位的设置来确定处理器是否执行该指令。在执行之前,处理器将条件属性与cpsr中的条件标志进行比较。如果它们匹配,则执行该指令;否则忽略该指令。

条件属性后缀附加在指令助记符上,并编码到指令中。表2.5列出了条件执行代码助记符。当没有条件助记符时,默认行为是将其设置为始终(AL)执行。
2.3 Pipeline

流水线是RISC处理器用于执行指令的机制。使用流水线可以在解码和执行其他指令的同时获取下一条指令,从而加速执行速度。可以将流水线视为汽车生产线的方式之一,每个阶段都执行特定的任务以制造汽车。图2.7显示了一个三级流水线:
■ Fetch从存储器中加载指令。
■ Decode识别要执行的指令。
■ Execute处理指令并将结果写回寄存器。
图2.8用一个简单的示例说明了流水线的工作原理。它展示了处理器按顺序获取、解码和执行的三条指令。在流水线填充后,每条指令需要一个周期来完成。

这三条指令按顺序放入流水线中。在第一个周期,核心从存储器中获取ADD指令。在第二个周期,核心获取SUB指令并解码ADD指令。在第三个周期中,SUB和ADD指令同时在流水线中移动。ADD指令被执行,SUB指令被解码,CMP指令被获取。这个过程称为填充流水线。流水线使得核心能够每个周期执行一条指令。
随着流水线长度的增加,每个阶段的工作量减少,这使得处理器可以达到更高的工作频率。这进而提高了性能。系统的延迟也会增加,因为在核心能够执行指令之前需要更多的周期来填充流水线。增加的流水线长度还意味着某些阶段之间可能存在数据依赖关系。您可以使用指令调度编写代码来减少这种依赖关系(有关指令调度的更多信息,请参阅第6章)。

每个ARM系列的流水线设计都不同。例如,ARM9核心将流水线长度增加到了五个阶段,如图2.9所示。ARM9添加了一个内存和写回阶段,使得ARM9能够以平均每兆赫处理1.1个Dhrystone MIPS,相比于ARM7而言,指令吞吐量增加了约13%。使用ARM9可以达到的最大核心频率也更高。
ARM10通过添加第六个阶段进一步增加了流水线长度,如图2.10所示。ARM10平均每兆赫能够处理1.3个Dhrystone MIPS,比ARM7处理器核心的吞吐量多约34%,但代价是更高的延迟。尽管ARM9和ARM10的流水线不同,但它们仍然使用与ARM7相同的流水线执行特性。针对ARM7编写的代码可以在ARM9或ARM10上执行。
2.3.1 Pipeline Executing Characteristics
在ARM流水线中,直到指令完全通过执行阶段,它才被处理。例如,ARM7流水线(具有三个阶段)只有在获取第四条指令时才执行一条指令。

图2.11展示了在ARM7流水线上的一条指令序列。MSR指令用于启用IRQ中断,只有当MSR指令完成流水线的执行阶段时才会发生。它清除cpsr中的I位以启用IRQ中断。一旦ADD指令进入流水线的执行阶段,IRQ中断就被启用。

图2.12说明了流水线和程序计数器pc的使用。在执行阶段,pc始终指向指令地址加上8字节。换句话说,pc始终指向正在执行的指令的地址加上两条指令。这在pc用于计算相对偏移时非常重要,并且是所有流水线的架构特性。需要注意的是,当处理器处于Thumb状态时,pc是指令地址加4。
流水线还有其他三个值得一提的特点。首先,执行分支指令或通过直接修改pc进行分支会导致ARM核心清空其流水线。
其次,ARM10使用分支预测,通过预测可能的分支并在指令执行之前加载新的分支地址,减少了流水线清空的影响。
第三,即使发生中断,执行阶段中的指令也会完成。流水线中的其他指令将被放弃,处理器将从向量表的适当入口开始填充流水线。
2.4 Exceptions, Interrupts, and the Vector Table
当发生异常或中断时,处理器会将pc设置为特定的内存地址。这个地址位于一个特殊的地址范围内,称为向量表。向量表中的条目是指令,用于跳转到专门设计用来处理特定异常或中断的程序。内存映射地址0x00000000保留给了向量表,它是一组32位的字。在某些处理器上,向量表可以选择地位于内存的较高地址处(从偏移0xffff0000开始)。像Linux和Microsoft的嵌入式产品这样的操作系统可以利用这个特性。

当发生异常或中断时,处理器会暂停正常执行,并开始从异常向量表中加载指令(见表2.6)。每个向量表条目包含一种指向特定例程起始处的分支指令形式:
- 复位向量是处理器上电时执行的第一条指令的位置。该指令将跳转到初始化代码。
- 未定义指令向量用于处理器无法解码的指令。
- 软件中断向量在执行SWI指令时被调用。SWI指令通常用作调用操作系统例程的机制。
- 预取中止向量发生在处理器尝试从没有正确访问权限的地址获取指令时。实际的中止发生在解码阶段。
- 数据中止向量类似于预取中止,但是当指令尝试在没有正确访问权限的情况下访问数据内存时引发。
- 中断请求向量由外部硬件用于中断处理器的正常执行流程。只有在cpsr中允许IRQ中断被屏蔽时,它才会被触发。
- 快速中断请求向量类似于中断请求,但为需要更快响应时间的硬件保留。只有在cpsr中允许FIQ中断被屏蔽时,它才会被触发。
2.5 Core Extensions
本节所涉及的硬件扩展是放置在ARM核心旁边的标准组件。它们提高了性能、管理资源并提供额外的功能,旨在为处理特定应用程序提供灵活性。每个ARM系列都有可用的不同扩展。
ARM在核心周围包装了三个硬件扩展:缓存和紧密耦合存储器、内存管理以及协处理器接口。
2.5.1 Cache and Tightly Coupled Memory
缓存是位于主存储器和核心之间的一块快速存储器块。它允许更高效地从某些类型的存储器中获取数据。有了缓存,处理器核心可以大部分时间运行而无需等待来自慢速外部存储器的数据。大多数基于ARM的嵌入式系统使用内部单级缓存。当然,并不是所有小型嵌入式系统都需要缓存所带来的性能提升。

ARM有两种形式的缓存。第一种是连接到冯·诺依曼风格的核心上。它将数据和指令结合到一个统一的缓存中,如图2.13所示。为简单起见,我们将连接内存系统与AMBA总线逻辑和控制的粘合逻辑称为“glue logic”。
相比之下,第二种形式连接到哈佛风格的核心上,具有独立的数据和指令缓存。
缓存提供了整体性能的增加,但以可预测的执行为代价。然而,对于实时系统来说,代码执行的可确定性至关重要,加载和存储指令或数据所需的时间必须是可预测的。这通过一种称为紧密耦合存储器(TCM)的存储器形式实现。TCM是靠近核心的快速SRAM,并保证获取指令或数据所需的时钟周期,这对于需要确定行为的实时算法至关重要。TCM在地址映射中作为内存出现,并且可以作为快速存储器进行访问。图2.14显示了一个带有TCM的处理器示例。

通过结合这两种技术,ARM处理器可以同时获得提高性能和可预测的实时响应。图2.15显示了一个具有缓存和TCM组合的核心示例。

2.5.2 Memory Management
嵌入式系统通常使用多个存储器设备。通常需要一种方法来帮助组织这些设备,并保护系统免受试图对硬件进行不适当访问的应用程序的影响。这是通过内存管理硬件的协助实现的。
ARM核心具有三种不同类型的内存管理硬件:没有提供保护的扩展、提供有限保护的内存保护单元(MPU)和提供全面保护的内存管理单元(MMU):
- 无保护内存是固定的,提供非常有限的灵活性。通常用于不需要防止恶意应用程序的小型简单嵌入式系统。
- MPU采用一种简单的系统,使用有限数量的内存区域。这些区域由一组特殊的协处理器寄存器控制,每个区域都定义了特定的访问权限。这种内存管理类型用于需要内存保护但没有复杂内存映射的系统。MPU在第13章中有详细说明。
- MMU是ARM上最全面的内存管理硬件。MMU使用一组转换表对内存进行精细控制。这些表存储在主存储器中,并提供虚拟地址到物理地址的映射以及访问权限。MMU适用于支持多任务的更复杂的平台操作系统。MMU在第14章中有详细说明。
这些内存管理硬件为系统提供了不同级别的保护和灵活性,以确保安全性和可靠性。
2.5.3 Coprocessors
协处理器可以附加到ARM处理器上。协处理器通过扩展指令集或提供配置寄存器来扩展核心的处理功能。可以通过协处理器接口将多个协处理器添加到ARM核心中。
可以通过一组专用的ARM指令访问协处理器,这些指令提供了一种加载-存储类型的接口。例如,考虑协处理器15:ARM处理器使用协处理器15寄存器来控制缓存、TCM和内存管理。
协处理器还可以通过提供一组特殊的新指令来扩展指令集。例如,可以将一组专门的指令添加到标准的ARM指令集中以处理矢量浮点(VFP)操作。
这些新指令在ARM流水线的解码阶段进行处理。如果解码阶段看到一个协处理器指令,则将其提供给相应的协处理器。但是,如果协处理器不存在或无法识别该指令,则ARM会引发一个未定义指令异常,从而允许在软件中模拟协处理器的行为。
2.6 Architecture Revisions
每个ARM处理器实现都执行特定的指令集架构(ISA),尽管一个ISA修订版本可能有多个处理器实现。
为了满足嵌入式市场的需求,ISA已经不断发展。ARM对这种演进进行了精心管理,以使在早期架构修订版上编写的代码也可以在后续架构的修订版上执行。
在我们继续解释架构的演进之前,我们必须介绍ARM处理器的命名规则。这个命名规则标识个别处理器并提供有关其功能集的基本信息。
2.6.1 Nomenclature
ARM使用图2.16所示的命名规则来描述处理器实现。在单词“ARM”之后的字母和数字表示处理器可能具有的特性。随着增加更多特性,将来可能会改变数字和字母的组合。需要注意的是,命名规则不包括架构修订信息。

关于ARM命名规则,还有一些其他要点:
- 所有在ARM7TDMI之后的ARM核心都包括了TDMI特性,即使在“ARM”标签之后没有这些字母。
- 处理器系列是共享相同硬件特性的处理器实现的组合。例如,ARM7TDMI、ARM740T和ARM720T都共享相同的系列特性,属于ARM7系列。
- JTAG由IEEE 1149.1标准测试访问端口和边界扫描架构描述。它是一种串行协议,用于在处理器核心和测试设备之间发送和接收调试信息。
- EmbeddedICE宏单元是内置在处理器中的调试硬件,允许设置断点和监视点。
- Synthesizable表示处理器核心以源代码形式提供,可以编译成易于EDA工具使用的形式。
2.6.2 Architecture Evolution
自从1985年首次推出ARM处理器以来,架构一直在不断发展。表2.7展示了从原始架构版本1到当前版本6的重要架构增强。ISA最显著的变化之一是在ARMv4T(ARM7TDMI处理器)中引入了Thumb指令集。

表2.8总结了程序状态寄存器的各个部分以及特定指令架构上某些功能的可用性。“All”指的是ARMv4架构及以上的版本。

2.7 ARM Processor Families
ARM设计了多个处理器,根据它们使用的核心进行分组,并形成了不同的系列。这些系列基于ARM7、ARM9、ARM10和ARM11核心。后缀数字7、9、10和11表示不同的核心设计。数字的增加代表性能和复杂性的提升。ARM8已经开发出来,但很快就被取代了。

表2.9粗略比较了ARM7、ARM9、ARM10和ARM11核心之间的属性。所引用的数字可以有很大差异,直接取决于制造工艺的类型和几何形状,这直接影响频率(MHz)和功耗(瓦特)。
在每个ARM系列中,都有多种存储管理、缓存和TCM处理器扩展的变体。ARM继续扩展可用系列的数量以及每个系列内的不同变体。
您可以找到其他执行ARM ISA的处理器,例如StrongARM和XScale。这些处理器是特定半导体公司的独特产品,比如英特尔。

表2.10总结了各种处理器的不同特点。下一小节将更详细地描述ARM系列,从ARM7系列开始。
2.7.1 ARM7 Family
ARM7核心采用冯·诺依曼(Von Neumann)风格的体系结构,其中数据和指令使用同一总线。该核心具有三级流水线,并执行ARMv4T体系结构指令集。
ARM7TDMI是ARM于1995年推出的新一代处理器中的第一个处理器。它目前是非常受欢迎的核心,广泛用于许多32位嵌入式处理器中。它提供了很好的性能与功耗比。ARM7TDMI处理器核心已经被全球许多顶级半导体公司授权,并且是首个包含Thumb指令集、快速乘法指令和EmbeddedICE调试技术的核心。
ARM7系列中一个显著的变体是ARM7TDMI-S。ARM7TDMI-S具有与标准ARM7TDMI相同的操作特性,但也可以进行可合成。ARM720T是ARM7系列中最灵活的成员,因为它包含了一个MMU(内存管理单元)。MMU的存在意味着ARM720T能够处理Linux和Microsoft嵌入式平台操作系统。该处理器还包括一个统一的8K缓存。通过设置协处理器15寄存器,向量表可以重定位到较高的地址。
另一个变体是ARM7EJ-S处理器,也是可合成的。ARM7EJ-S与众不同,它包含一个五级流水线,并执行ARMv5TEJ指令。这个版本的ARM7是唯一一个同时提供Java加速和增强指令,但没有任何内存保护的版本。
2.7.2 ARM9 Family
ARM9系列于1997年宣布推出。由于具有五级流水线,ARM9处理器可以以更高的时钟频率运行,比ARM7系列更快。额外的流水线阶段提高了处理器的整体性能。内存系统经过重新设计,采用了哈佛结构,将数据D和指令I总线分离。
ARM9系列的第一个处理器是ARM920T,其中包含单独的D + I缓存和MMU。这个处理器可以被需要虚拟内存支持的操作系统使用。ARM922T是ARM920T的一个变体,但D + I缓存大小为原来的一半。
ARM940T包括较小的D + I缓存和MPU。ARM940T专为不需要平台操作系统的应用程序设计。ARM920T和ARM940T都执行v4T指令架构。
ARM9系列的下一个处理器基于ARM9E-S核心。这个核心是带有E扩展的ARM9核心的可合成版本。有两个变体:ARM946E-S和ARM966E-S。它们都执行v5TE指令架构。它们还支持可选的嵌入式跟踪宏单元(ETM),允许开发人员实时跟踪处理器上的指令和数据执行。这在调试具有时间关键片段的应用程序时非常重要。
ARM946E-S包括TCM、缓存和MPU。TCM和缓存的大小可以配置。该处理器专为需要确定性实时响应的嵌入式控制应用程序设计。相比之下,ARM966E没有MPU和缓存扩展,但具有可配置的TCM。
ARM9产品线中最新的核心是ARM926EJ-S可合成处理器核心,于2000年宣布推出。它专为小型便携式Java设备设计,如3G手机和个人数字助理(PDA)。ARM926EJ-S是第一个包含Jazelle技术的ARM处理器核心,该技术可以加速Java字节码执行。它具有MMU、可配置的TCM和带有零等待状态或非零等待状态存储器的D + I缓存。
2.7.3 ARM10 Family
ARM10于1999年宣布推出,旨在提供更高的性能。它将ARM9的流水线扩展到六个阶段。它还支持可选的向量浮点(VFP)单元,为ARM10流水线增加了第七个阶段。VFP显著提高了浮点性能,并符合IEEE 754.1985浮点标准。
ARM1020E是第一个使用ARM10E核心的处理器。类似于ARM9E,它包括增强的E指令。它具有独立的32K D + I缓存,可选的向量浮点单元和MMU。ARM1020E还具有双64位总线接口,以提高性能。
ARM1026EJ-S与ARM926EJ-S非常相似,但同时具备MPU和MMU。这个处理器具有ARM10的性能和ARM926EJ-S的灵活性。
2.7.4 ARM11 Family
ARM1136J-S于2003年宣布推出,旨在为高性能和功耗效率应用程序设计。ARM1136J-S是第一个执行ARMv6指令架构的处理器实现。它采用了八级流水线,包括独立的加载-存储和算术流水线。ARMv6指令中包含用于媒体处理的单指令多数据(SIMD)扩展,专门设计以提高视频处理性能。
ARM1136JF-S是在ARM1136J-S基础上增加了向量浮点单元,用于进行快速浮点运算。
2.7.5 Specialized Processors
StrongARM最初由Digital Semiconductor共同开发,现在由英特尔独家许可。它在个人数字助理(PDA)和对低功耗性能要求较高的应用程序中非常受欢迎。它采用哈佛结构,具有独立的D + I缓存。StrongARM是第一个具有五级流水线的高性能ARM处理器,但不支持Thumb指令集。
英特尔的XScale是StrongARM的后续产品,提供了显著的性能增加。在撰写本文时,XScale被引用为能够达到1 GHz的运行速度。XScale执行架构v5TE指令。它采用哈佛结构,与StrongARM相似,也包括一个MMU。
SC100则处于性能谱的另一端。它专为低功耗安全应用而设计。SC100是第一个SecurCore,基于带有MPU的ARM7TDMI核心。该核心体积小、电压和电流要求低,非常适用于智能卡应用。
2.8 Summary
在这一章中,我们专注于实际的ARM处理器的硬件基础知识。ARM处理器可以抽象为八个组成部分:ALU(算术逻辑单元)、移位器、乘累加器、寄存器文件、指令解码器、地址寄存器、增量器和符号扩展器。
ARM有三个指令集:ARM、Thumb和Jazelle。寄存器文件包含37个寄存器,但在任何时刻只有17或18个寄存器可访问;其余的根据处理器模式进行分组。当前处理器模式存储在cpsr(当前程序状态寄存器)中。它保存处理器核心的当前状态,包括中断屏蔽、条件标志和状态。状态决定正在执行哪个指令集。
ARM处理器由核心和与总线接口的周边组件组成。核心扩展包括以下内容:
- 缓存用于提高整体系统性能。
- TCM(Tightly-Coupled Memory)用于提高确定性实时响应。
- 内存管理用于组织内存和保护系统资源。
- 协处理器用于扩展指令集和功能。协处理器15控制缓存、TCM和内存管理。
ARM处理器是特定指令集架构(ISA)的实现。从第一个ARM处理器设计以来,ISA不断改进。处理器被分为具有相似特征的实现系列(ARM7、ARM9、ARM10和ARM11)。
Chapter3 Introduction to the ARM Instruction Set
ARM指令集介绍是本书的基础章节,因为这里提供的信息将贯穿整本书。因此,在深入探讨优化和高效算法之前,我们首先进行了介绍。本章介绍了最常见和最有用的ARM指令,并构建在上一章所涵盖的ARM处理器基础知识之上。第4章介绍了Thumb指令集,附录A给出了所有ARM指令的完整描述。
不同的ARM架构修订版本支持不同的指令。然而,新的修订版本通常会添加指令并保持向后兼容性。你在ARMv4T架构下编写的代码应该可以在ARMv5TE处理器上执行。表3.1提供了ARMv5E指令集架构(ISA)中可用的所有ARM指令的完整列表。该ISA包括所有核心ARM指令以及ARM指令集中的一些新功能。"ARM ISA"列出了引入该指令的ISA修订版本。一些指令在后续架构中具有扩展功能;例如,CDP指令有一个名为CDP2的ARMv5变体。类似地,像LDR这样的指令具有ARMv5的扩展,但不需要新的或扩展的助记符。


我们使用具有预条件和后置条件的示例来说明处理器的操作,描述指令或指令执行之前和之后的寄存器和内存。我们将以0x为前缀表示十六进制数,以0b为前缀表示二进制数。示例遵循以下格式:
PRE <预条件>
<指令/指令集>
POST <后置条件>
在<预条件>和<后置条件>中,内存表示为 mem<数据大小>[地址]
这表示从给定字节地址开始的数据大小位内存。例如,mem32[1024]表示从1 KB地址开始的32位值。
ARM指令处理寄存器中保存的数据,并且只通过加载和存储指令来访问内存。ARM指令通常使用两个或三个操作数。例如,下面的ADD指令将存储在寄存器r1和r2中的两个值(源寄存器)相加。它将结果写入寄存器r3(目标寄存器)。

在接下来的章节中,我们将按照指令类别来检视ARM指令的功能和语法,包括数据处理指令、分支指令、加载存储指令、软件中断指令以及程序状态寄存器指令。
3.1 Data Processing Instructions
数据处理指令用于在寄存器中操作数据。它们包括移动指令、算术指令、逻辑指令、比较指令和乘法指令。大多数数据处理指令可以使用移位器对其操作数进行处理。
如果在数据处理指令上使用S后缀,则会更新cpsr中的标志位。移动和逻辑操作会更新进位标志C、负数标志N和零标志Z。进位标志由移位操作的结果中的最后一位设置。N标志被设置为结果的第31位。如果结果为零,Z标志将被设置为1。
3.1.1 Move Instructions
Move是最简单的ARM指令。它将一个寄存器或立即数N的值复制到目标寄存器Rd中。该指令用于设置初始值和在寄存器之间传输数据。
语法: <instruction>{<cond>}{S} Rd, N

表3.3将在第3.1.2节中呈现,它给出了所有数据处理指令的第二个操作数N允许的完整描述。通常情况下,它可以是寄存器Rm或以#为前缀的常数。
示例3.1
这个例子展示了一个简单的移动指令。MOV指令将寄存器r5的内容复制到寄存器r7中,在这个例子中,将值5复制到寄存器r7,并覆盖了r7中原有的值8。
PRE
r5 = 5
r7 = 8
MOV r7, r5 ; let r7 = r5
POST
r5 = 5
r7 = 53.1.2 Barrel Shifter
在示例3.1中,我们展示了一个MOV指令,其中N是一个简单的寄存器。但是,N不仅可以是寄存器或立即数,还可以是经过移位器预处理后由数据处理指令使用的寄存器Rm。数据处理指令在算术逻辑单元(ALU)中进行处理。
ARM处理器的一个独特而强大的特性是能够在进入ALU之前,将一个源寄存器中的32位二进制模式向左或向右移动特定的位置数。这种移位操作提高了许多数据处理操作的功能和灵活性。
有些数据处理指令不使用移位器,例如乘法指令MUL、计算前导零CLZ和有符号饱和32位加法指令QADD。
预处理或移位操作发生在指令的周期内。这对于将常量加载到寄存器中,并实现快速乘法或2的幂次方除法特别有用。

为了说明移位器,我们将采用图3.1中的例子,并在移动指令示例中添加一个移位操作。寄存器Rn在进入ALU之前没有经过任何寄存器的预处理。图3.1显示了ALU和移位器之间的数据流动。
示例3.2
PRE
r5 = 5
r7 = 8
MOV r7, r5, LSL #2 ; let r7 = r5*4 = (r5 << 2)
POST
r5 = 5
r7 = 20我们在将寄存器Rm移动到目标寄存器之前,对其应用逻辑左移(LSL)。这与将标准的C语言移位运算符<<应用于寄存器相同。MOV指令将移位运算符的结果N复制到寄存器Rd中。N表示在表3.2中描述的LSL操作的结果。

这个例子将寄存器r5乘以四,然后将结果放入寄存器r7。
你可以在移位器中使用的五种不同的移位操作在表3.2中进行了总结。

图3.2演示了逻辑左移一位。例如,位0的内容被移动到位1,位0被清除。C标志位会根据移出寄存器的最后一位进行更新。这是原始值的第(32-y)位,其中y是移位量。当y大于1时,将位移y个位置与执行一次位移一样,只是重复执行y次而已。
示例3.3
这个示例展示了一个MOVS指令,它将寄存器r1左移一位。这相当于将寄存器r1乘以21的值。正如你所看到的,因为指令助记符中有S后缀,所以C标志位在cpsr中得到了更新。
PRE
cpsr = nzcvqiFt_USER
r0 = 0x00000000
r1 = 0x80000004
MOVS r0, r1, LSL #1
POST
cpsr = nzCvqiFt_USER
r0 = 0x00000008
r1 = 0x80000004表3.3列出了数据处理指令中可用的不同移位操作的语法。第二个操作数N可以是以#为前缀的立即常数,寄存器的值Rm,或经过移位处理的Rm的值。
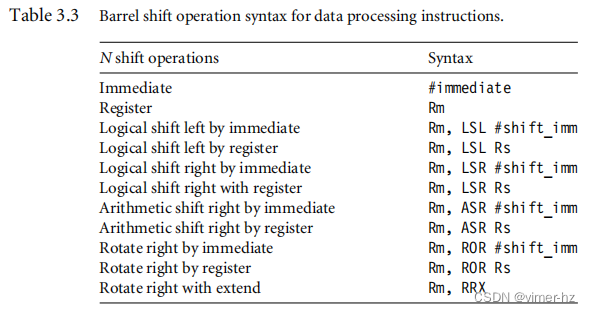
3.1.3 Arithmetic Instructions
算术指令实现了32位有符号和无符号值的加法和减法。
语法: <instruction>{<cond>}{S} Rd, Rn, N

N是移位器操作的结果。移位器操作的语法在表3.3中显示。
示例3.4
这个简单的减法指令将寄存器r2中存储的值从寄存器r1中存储的值中减去。结果存储在寄存器r0中。
PRE
r0 = 0x00000000
r1 = 0x00000002
r2 = 0x00000001
SUB r0, r1, r2
POST
r0 = 0x00000001示例3.5
这个反向减法指令(RSB)将常数值#0减去r1的值,并将结果写入r0。你可以使用这个指令来对数字取反。
PRE
r0 = 0x00000000
r1 = 0x00000077
RSB r0, r1, #0 ; Rd = 0x0 - r1
POST
r0 = -r1 = 0xffffff89示例3.6
SUBS指令在递减循环计数器时非常有用。在这个例子中,我们从寄存器r1中存储的值1中减去立即值1。结果值0被写入寄存器r1。cpsr被更新,其中ZC标志被设置。
PRE
cpsr = nzcvqiFt_USER
r1 = 0x00000001
SUBS r1, r1, #1
POST
cpsr = nZCvqiFt_USER
r1 = 0x000000003.1.4 Using the Barrel Shifter with Arithmetic Instructions
ARM指令集中提供了广泛的第二操作数移位选项,这是一个非常强大的特性。示例3.7演示了在算术指令中使用内联移位器的用法。该指令将寄存器r1中存储的值乘以3。
示例3.7
首先,将寄存器r1向左移动一位,得到r1的两倍值。然后,ADD指令将移位操作的结果与寄存器r1相加。最终将计算结果传送到寄存器r0中,等于寄存器r1中存储值的三倍。
PRE
r0 = 0x00000000
r1 = 0x00000005
ADD r0, r1, r1, LSL #1
POST
r0 = 0x0000000f
r1 = 0x000000053.1.5 Logical Instructions
逻辑指令对两个源寄存器执行按位逻辑操作。
语法: <instruction>{<cond>}{S} Rd, Rn, N

示例3.8
这个示例展示了寄存器r1和r2之间的逻辑或操作。结果存储在寄存器r0中。
PRE
r0 = 0x00000000
r1 = 0x02040608
r2 = 0x10305070
ORR r0, r1, r2
POST
r0 = 0x12345678示例3.9
这个例子展示了一个更复杂的逻辑指令,称为BIC,它执行逻辑位清除操作。
PRE
r1 = 0b1111
r2 = 0b0101
BIC r0, r1, r2
POST
r0 = 0b1010
This is equivalent to
Rd = Rn AND NOT(N)在这个例子中,寄存器r2包含一个二进制模式,其中r2中的每个二进制1会清除寄存器r1中相应的位位置。这个指令在清除状态位时特别有用,并经常用于更改cpsr中的中断屏蔽位。逻辑指令仅在有S后缀时更新cpsr标志位。这些指令可以像算术指令一样使用移位的第二操作数。
3.1.6 Comparison Instructions
比较指令用于将寄存器与32位值进行比较或测试。它们根据结果更新cpsr标志位,但不影响其他寄存器。在标志位设置后,可以通过条件执行来改变程序流程。关于条件执行的更多信息,请参阅第3.8节。对于比较指令,不需要使用S后缀来更新标志位。
语法: <instruction>{<cond>} Rn, N

N是移位操作的结果。移位操作的语法在表3.3中显示。
示例3.10
这个例子展示了一个CMP比较指令。在执行该指令之前,可以看到寄存器r0和r9都是相等的。执行前,z标志位的值为0(小写z表示)。执行后,z标志位变为1(大写Z表示)。这个变化表示相等。
PRE
cpsr = nzcvqiFt_USER
r0 = 4
r9 = 4
CMP r0, r9
POST
cpsr = nZcvqiFt_USERCMP指令实际上是一个减法指令,结果被丢弃;同样,TST指令是逻辑与操作,TEQ是逻辑异或操作。对于每个指令,结果被丢弃,但条件位在cpsr中被更新。重要的是要理解,比较指令只修改cpsr的条件标志位,不影响被比较的寄存器。
3.1.7 Multiply Instructions
乘法指令将一对寄存器的内容相乘,并根据指令的不同将结果与另一个寄存器累加。长乘法将结果累积到代表64位值的一对寄存器中。最终结果放置在目标寄存器或一对寄存器中。
语法: MLA{<cond>}{S} Rd, Rm, Rs, Rn
MUL{<cond>}{S} Rd, Rm, Rs

Syntax: <instruction>{<cond>}{S} RdLo, RdHi, Rm, Rs
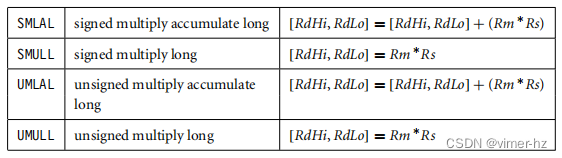
执行乘法指令所需的周期数取决于处理器的实现。对于某些实现,周期计时还取决于寄存器Rs中的值。有关周期计时的更多详细信息,请参阅附录D。
示例3.11
这个例子展示了一个简单的乘法指令,将寄存器r1和r2相乘,并将结果放置在寄存器r0中。在这个例子中,寄存器r1的值为2,r2的值也为2。结果4被放置在寄存器r0中。
PRE
r0 = 0x00000000
r1 = 0x00000002
r2 = 0x00000002
MUL r0, r1, r2 ; r0 = r1*r2
POST
r0 = 0x00000004
r1 = 0x00000002
r2 = 0x00000002长乘法指令(SMLAL、SMULL、UMLAL和UMULL)产生一个64位的结果。该结果太大,无法放入一个32位寄存器,因此结果被放置在两个标记为RdLo和RdHi的寄存器中。RdLo保存64位结果的低32位,而RdHi保存64位结果的高32位。示例3.12展示了一个长无符号乘法指令的示例。
示例3.12
该指令将寄存器r2和r3相乘,并将结果放置在寄存器r0和r1中。寄存器r0包含64位结果的低32位,而寄存器r1包含64位结果的高32位。
PRE
r0 = 0x00000000
r1 = 0x00000000
r2 = 0xf0000002
r3 = 0x00000002
UMULL r0, r1, r2, r3 ; [r1,r0] = r2*r3
POST
r0 = 0xe0000004 ; = RdLo
r1 = 0x00000001 ; = RdHi3.2 Branch Instructions
分支指令改变了程序的执行流程,用于跳转到不同的地址或调用一个子程序。这种类型的指令允许程序具有子例程、if-then-else结构和循环。执行流程的改变会使程序计数器PC指向一个新的地址。ARMv5E指令集包括四种不同的分支指令。
语法:
B{<cond>} label
BL{<cond>} label
BX{<cond>} Rm
BLX{<cond>} label | Rm

地址标签以带符号的PC相对偏移量的形式存储在指令中,并且必须在分支指令附近的32MB范围内。T代表cpsr中的Thumb位。当设置Thumb时,ARM会切换到Thumb状态。
示例3.13
这个例子展示了前向分支和后向分支。由于这些循环是特定地址的,我们不包括前置和后置条件。前向分支跳过了三个指令。后向分支创建了一个无限循环。
B forward
ADD r1, r2, #4
ADD r0, r6, #2
ADD r3, r7, #4
forward
SUB r1, r2, #4
backward
ADD r1, r2, #4
SUB r1, r2, #4
ADD r4, r6, r7
B backward分支指令用于改变执行流程。大多数汇编器通过使用标签来隐藏分支指令的编码细节。在这个例子中,"forward"和"backward"是标签。分支标签位于行的开头,用于标记一个地址,汇编器可以稍后使用该地址来计算分支偏移量。
示例3.14
带有链接的分支指令(BL)类似于B指令,但它会用返回地址覆盖链接寄存器LR,并执行一个子程序调用。此示例显示了一个简单的代码片段,使用BL指令跳转到一个子程序。要从子程序返回,您可以将链接寄存器复制到PC。
BL subroutine ; branch to subroutine
CMP r1, #5 ; compare r1 with 5
MOVEQ r1, #0 ; if (r1==5) then r1 = 0
:
subroutine
<subroutine code>
MOV pc, lr ; return by moving pc = lr分支交换(BX)和带链接的分支交换(BLX)是第三种类型的分支指令。BX指令使用存储在寄存器Rm中的绝对地址。它主要用于在Thumb代码中进行分支,如第4章所示。cpsr中的T位由分支寄存器的最低有效位更新。类似地,BLX指令使用最低有效位更新cpsr的T位,并额外设置链接寄存器以存储返回地址。
3.3 Load-Store Instructions
加载存储指令用于在内存和处理器寄存器之间传输数据。有三种类型的加载存储指令:单寄存器传输、多寄存器传输和交换。
3.3.1 Single-Register Transfer
这些指令用于在寄存器和内存之间传输单个数据项。支持的数据类型包括有符号和无符号的字(32位)、半字(16位)和字节。以下是各种加载存储单寄存器传输指令的语法:
语法:<LDR|STR>{<cond>}{B} Rd,addressing1
LDR{<cond>}SB|H|SH Rd, addressing2
STR{<cond>}H Rd, addressing2


示例: 3.15 LDR和STR指令可以在与要加载或存储的数据类型大小相同的边界对齐上加载和存储数据。例如,LDR只能在内存地址是四字节的倍数(0、4、8等)上加载32位字。下面是一个示例,首先从寄存器r1中的内存地址加载数据,然后将其存储回同一内存地址。
;
; load register r0 with the contents of
; the memory address pointed to by register
; r1.
;
LDR r0, [r1]
; = LDR r0, [r1, #0]
;
; store the contents of register r0 to
; the memory address pointed to by
; register r1.
;
STR r0, [r1]
; = STR r0, [r1, #0]第一条指令从存储在寄存器r1中的地址加载一个字,并将其放入寄存器r0中。第二条指令则相反,将寄存器r0中的内容存储到寄存器r1中包含的地址中。寄存器r1的偏移量为零。寄存器r1被称为基地址寄存器。
3.3.2 Single-Register Load-Store Addressing Modes
ARM指令集提供了多种内存寻址模式。这些模式包含一种索引方法:带写回的预索引(preindex with writeback)、预索引和后索引(详见表3.4)。

示例3.16中的带写回的预索引(preindex with writeback)模式通过将基址寄存器与地址偏移相加计算出一个地址,并将该新地址更新到基址寄存器中。相比之下,预索引(preindex)模式与带写回的预索引模式相同,但不会更新基址寄存器的值。后索引(postindex)模式只在使用地址后才更新基址寄存器的值。预索引模式适用于访问数据结构中的元素。后索引和带写回的预索引模式适用于遍历数组。
PRE
r0 = 0x00000000
r1 = 0x00090000
mem32[0x00009000] = 0x01010101
mem32[0x00009004] = 0x02020202
LDR r0, [r1, #4]!
Preindexing with writeback:
POST(1) r0 = 0x02020202
r1 = 0x00009004
LDR r0, [r1, #4]
Preindexing:
POST(2) r0 = 0x02020202
r1 = 0x00009000
LDR r0, [r1], #4
Postindexing:
POST(3) r0 = 0x01010101
r1 = 0x00009004示例3.15使用了预索引(preindex)方法。这个例子展示了每种索引方法对寄存器r1中保存的地址以及加载到寄存器r0中的数据产生的影响。每条指令都展示了相同前提条件下索引方法的结果。
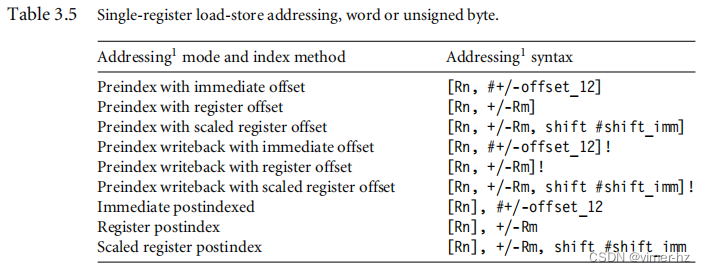
在特定的加载(load)或存储(store)指令中可用的寻址模式取决于指令类别。表3.5展示了加载和存储32位字或无符号字节的寻址模式。
"±"表示带符号的偏移量或寄存器,标识其是基址寄存器Rn的正偏移或负偏移。基址寄存器是指向内存中一个字节的指针,而偏移量指定了字节数。
"Immediate"表示地址是使用基址寄存器和指令中编码的12位偏移量计算得出的。"Register"表示地址是使用基址寄存器和特定寄存器的内容计算得出的。"Scaled"表示地址是使用基址寄存器和一个移位操作计算得出的。


表3.6给出了LDR指令的不同变体的示例。表3.7展示了加载和存储指令使用16位半字或有符号字节数据时可用的寻址模式。

这些操作不能使用移位操作器。没有STRSB或STRSH指令,因为STRH存储有符号和无符号的半字;类似地,STRB存储有符号和无符号的字节。表3.8展示了STRH指令的变体。以上是例子中关于索引方法和寻址模式的说明。这些信息用于描述不同的内存访问方式和操作指令的使用规则。
3.3.3 Multiple-Register Transfer
加载-存储多个指令可以在一条指令中在内存和处理器之间传输多个寄存器。传输是从一个指向内存的基址寄存器Rn开始进行的。相比于逐个传输寄存器的单个传输指令,多寄存器传输指令在移动数据块、保存和恢复上下文和堆栈时更加高效。
加载-存储多个指令可能会增加中断延迟。ARM架构的实现通常不会在指令执行过程中中断它们。例如,在ARM7上,加载多个指令需要2 + Nt个周期,其中N是要加载的寄存器数量,t是每个连续访问内存所需的周期数。如果发生了中断,则中断对加载-存储多个指令没有影响,直到该指令执行完成。编译器(例如armcc)提供了一个开关来控制在加载-存储操作中传输的寄存器的最大数量,从而限制了最大的中断延迟。
语法如下:<LDM|STM>{<cond>}<addressing mode> Rn{!},<registers>{ˆ}


表格3.9展示了加载-存储多个指令的不同寻址模式。在这里,N是寄存器列表中的寄存器数量。可以将当前寄存器组中的任意子集传输到内存或从内存中获取。基址寄存器Rn确定加载-存储多个指令的源地址或目标地址。在传输之后,可以选择性地更新该寄存器。当寄存器Rn后面跟着感叹号(!)字符时,就会发生这种情况,类似于使用预索引和写回的单个寄存器加载-存储操作。
例如3.17
在这个例子中,寄存器r0是基址寄存器Rn,后面跟着感叹号(!),表示该寄存器在指令执行后将被更新。在加载多个指令中,你会注意到寄存器没有逐个列出。相反,“-”字符用于标识一系列寄存器。在本例中,范围从寄存器r1到r3(包括r1和r3)。
每个寄存器也可以使用逗号分隔,放在“{”和“}”括号中进行列表。
PRE
mem32[0x80018] = 0x03
mem32[0x80014] = 0x02
mem32[0x80010] = 0x01
r0 = 0x00080010
r1 = 0x00000000
r2 = 0x00000000
r3 = 0x00000000
LDMIA r0!, {r1-r3}
POST
r0 = 0x0008001c
r1 = 0x00000001
r2 = 0x00000002
r3 = 0x00000003图3.3显示了一个图形表示。基址寄存器r0在PRE条件下指向内存地址0x80010。内存地址0x80010,0x80014和0x80018分别包含值1、2和3。执行加载多个指令后,寄存器r1、r2和r3包含了这些值,如图3.4所示。在最后一个加载的字之后,基址寄存器r0现在指向内存地址0x8001c。

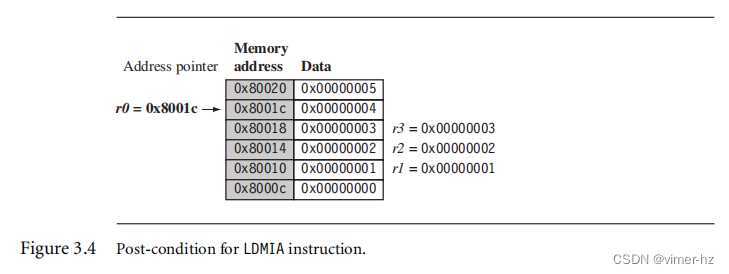
现在将LDMIA指令替换为在LDMIB指令之前进行递增的加载多个指令,并使用相同的PRE条件。忽略由寄存器r0指向的第一个字,并从下一个内存位置加载寄存器r1,如图3.5所示。执行后,寄存器r0现在指向最后加载的内存位置。这与LDMIA示例相反,它指向了下一个内存位置。

加载-存储多个指令的递减版本DA和DB会递减起始地址,然后按升序存储到内存位置。这相当于降序访问内存,但以相反的顺序访问寄存器列表。通过增量和递减加载多个指令,您可以正向或反向访问数组。它们还允许堆栈的推入和弹出操作,在本节后面会有进一步说明。
表格3.10显示了一组加载-存储多个指令对。如果使用带有基址更新的存储指令,那么相同数量寄存器的配对加载指令将重新加载数据并恢复基址指针。当您需要暂时保存一组寄存器并在以后恢复它们时,这是非常有用的。
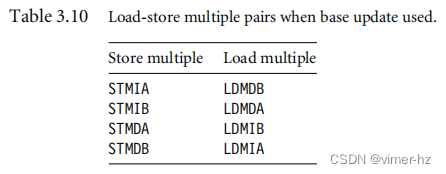
例子3.18
这个例子展示了一个递增前STM指令,后跟一个递减后LDM指令。
PRE
r0 = 0x00009000
r1 = 0x00000009
r2 = 0x00000008
r3 = 0x00000007
STMIB r0!, {r1-r3}
MOV r1, #1
MOV r2, #2
MOV r3, #3
PRE(2) r0 = 0x0000900c
r1 = 0x00000001
r2 = 0x00000002
r3 = 0x00000003
LDMDA r0!, {r1-r3}
POST r0 = 0x00009000
r1 = 0x00000009
r2 = 0x00000008
r3 = 0x00000007STMIB指令将值7、8、9存储到内存中。然后我们破坏了寄存器r1到r3的值。
LDMDA指令重新加载了原始值并恢复了基址指针r0。
例子3.19
我们用一个块内存复制的例子来说明加载-存储多个指令的用法。这个例子是一个简单的例程,它将32字节的块从源地址位置复制到目标地址位置。
这个例子有两个加载-存储多个指令,它们使用相同的递增后寻址模式。
; r9 points to start of source data
; r10 points to start of destination data
; r11 points to end of the source
loop
; load 32 bytes from source and update r9 pointer
LDMIA r9!, {r0-r7}
; store 32 bytes to destination and update r10 pointer
STMIA r10!, {r0-r7} ; and store them
; have we reached the end
CMP r9, r11
BNE loop这个例程在执行代码之前依赖于寄存器r9、r10和r11的设置。
寄存器r9和r11确定要复制的数据,寄存器r10指向要复制数据的目标内存位置。LDMIA将寄存器r9指向的数据加载到寄存器r0到r7中。它还更新了r9,以指向下一个要复制的数据块。STMIA将寄存器r0到r7的内容复制到寄存器r10指向的目标内存地址。它还更新了r10,以指向下一个目标位置。CMP和BNE比较指针r9和r11,检查是否已经到达了块复制的末尾。如果块复制完成,则程序终止;否则,循环使用更新后的r9和r10的值重复执行。
BNE是带有条件助记符NE(不等)的分支指令B。如果前面的比较指令将条件标志设置为不相等,则执行分支指令。
图3.6显示了块内存复制的内存映射以及例程如何在内存中移动。理论上,这个循环可以用两条指令传输32字节(8个字),最大可能的吞吐量为每秒46 MB在33 MHz的速度下进行传输。这些数字假设存在一个完美的内存系统和快速的内存。

3.3.3.1 Stack Operations
ARM架构使用加载-存储多重指令来执行堆栈操作。弹出操作(从堆栈中移除数据)使用加载多重指令;类似地,推入操作(将数据放入堆栈)使用存储多重指令。
在使用堆栈时,您必须决定堆栈在内存中是向上增长还是向下增长。堆栈可以是升序(A)或降序(D)。升序堆栈向更高的内存地址增长,而降序堆栈向较低的内存地址增长。
当使用满堆栈(F)时,堆栈指针sp指向最后一个被使用或满的位置(即sp指向堆栈上的最后一个项目)。相反,如果使用空堆栈(E),sp指向第一个未使用或空的位置(即它指向堆栈上最后一个项目之后的位置)。

为了支持堆栈操作,有许多加载-存储多重寻址模式别名可用(参见表3.11)。在pop列旁边是实际的加载多重指令等效指令。例如,完整的升序堆栈将在加载多重指令后附加标注FA - LDMFA。这将被转换为LDMDA指令。
ARM规定了一个ARM-Thumb过程调用标准(ATPCS),定义了如何调用子程序以及如何分配寄存器。在ATPCS中,堆栈被定义为满降序堆栈。因此,LDMFD和STMFD指令分别提供了弹出和推入功能。
例子3.20
STMFD指令将寄存器推入堆栈并更新sp。图3.7显示了对满减序堆栈进行推入的情况。您可以看到,当堆栈增长时,堆栈指针指向堆栈中最后一个满的条目。
PRE
r1 = 0x00000002
r4 = 0x00000003
sp = 0x00080014
STMFD sp!, {r1,r4}
POST
r1 = 0x00000002
r4 = 0x00000003
sp = 0x0008000c
与之相反,例子3.21中的图3.8显示了在空堆栈上进行推入操作,使用的是STMED指令。STMED指令将寄存器推入堆栈,但会更新寄存器sp,使其指向下一个空位置。
PRE
r1 = 0x00000002
r4 = 0x00000003
sp = 0x00080010
STMED sp!, {r1,r4}
POST
r1 = 0x00000002
r4 = 0x00000003
sp = 0x00080008处理受检堆栈时,需要保留三个属性:堆栈基址、堆栈指针和堆栈限制。堆栈基址是堆栈在内存中的起始地址。堆栈指针最初指向堆栈基址;随着数据被推入堆栈,堆栈指针向内存递减,并持续指向堆栈顶部。 如果堆栈指针超过了堆栈限制,那么就会发生堆栈溢出错误。下面是一小段代码,用于检查降序堆栈的堆栈溢出错误:
; check for stack overflow
SUB sp, sp, #size
CMP sp, r10
BLLO _stack_overflow ; conditionATPCS将寄存器r10定义为堆栈限制或sl。这是可选的,因为只有在启用堆栈检查时才会使用它。BLLO指令是带链接的分支指令,加上条件词LO。如果在新项目被推入堆栈后,sp小于寄存器r10,则表示发生了堆栈溢出错误。如果堆栈指针回到堆栈基址之前,那么堆栈下溢错误就会发生。
3.3.4 Swap Instruction
交换指令是加载-存储指令的特例。它将内存中的内容与寄存器中的内容进行交换。这个指令是原子操作——它在同一个总线操作中读取和写入一个位置,防止其他指令在它完成之前读取或写入该位置。
语法:SWP{B}{<cond>} Rd,Rm,[Rn]

交换指令不能被其他任何指令或总线访问打断。我们说系统在事务完成之前"持有总线"。
示例3.22
交换指令将内存中的一个字加载到寄存器r0,并用寄存器r1覆盖内存。
PRE
mem32[0x9000] = 0x12345678
r0 = 0x00000000
r1 = 0x11112222
r2 = 0x00009000
SWP r0, r1, [r2]
POST
mem32[0x9000] = 0x11112222
r0 = 0x12345678
r1 = 0x11112222
r2 = 0x00009000这条指令在操作系统中实现信号量和互斥时非常有用。从语法可以看出,这条指令还可以有一个字节大小的限定符B,因此可以进行字和字节的交换。
示例3.23
这个示例展示了一个简单的数据保护器,可以用来防止其他任务对数据进行写入。SWP指令在事务完成之前"持有总线"。
spin
MOV r1, =semaphore
MOV r2, #1
SWP r3, r2, [r1] ; hold the bus until complete
CMP r3, #1
BEQ spin信号量指向的地址要么包含值0,要么包含值1。当信号量等于1时,表示该服务正在被另一个进程使用。该例程将不断循环,直到该服务被其他进程释放,也就是说,直到信号量地址位置包含值0为止。
3.4 Software Interrupt Instruction
软件中断指令(SWI)引发软件中断异常,为应用程序提供调用操作系统例程的机制。
语法:SWI{<cond>} SWI_number

当处理器执行SWI指令时,它将程序计数器pc设置为向量表中的偏移量0x8。该指令还强制处理器模式设置为SVC,允许以特权模式调用操作系统例程。
每个SWI指令都有一个关联的SWI编号,用于表示特定的函数调用或功能。
示例3.24
这是一个简单的SWI调用示例,使用SWI编号0x123456,被ARM工具包用作调试SWI。通常,SWI指令在用户模式下执行。
PRE
cpsr = nzcVqift_USER
pc = 0x00008000
lr = 0x003fffff; lr = r14
r0 = 0x12
0x00008000 SWI 0x123456
POST
cpsr = nzcVqIft_SVC
spsr = nzcVqift_USER
pc = 0x00000008
lr = 0x00008004
r0 = 0x12由于SWI指令用于调用操作系统例程,因此需要某种形式的参数传递。这是通过寄存器来实现的。在这个例子中,寄存器r0用于传递参数0x12。返回值也通过寄存器传递回来。
需要一个处理SWI调用的代码来处理调用SWI的操作。处理程序使用执行指令的地址确定SWI编号,该地址是从链接寄存器lr计算得出的。
SWI编号的确定方式为
SWI_Number = <SWI指令> AND NOT(0xff000000)
在这里,SWI指令是处理器执行的实际32位SWI指令。
示例3.25
这个例子展示了一个SWI处理程序实现的开头部分。代码片段确定所调用的SWI编号,并将该编号放入寄存器r10中。从这个示例可以看出,加载指令首先将完整的SWI指令复制到寄存器r10中。BIC指令屏蔽了指令的高位,只留下了SWI编号。我们假设SWI是从ARM状态调用的。
SWI_handler
;
; Store registers r0-r12 and the link register
;
STMFD sp!, {r0-r12, lr}
; Read the SWI instruction
LDR r10, [lr, #-4]
; Mask off top 8 bits
BIC r10, r10, #0xff000000
; r10 - contains the SWI number
BL service_routine
; return from SWI handler
LDMFD sp!, {r0-r12, pc}ˆ寄存器r10中的数字随后由SWI处理程序用于调用相应的SWI服务例程。
3.5 Program Status Register Instructions
ARM指令集提供了两个指令,用于直接控制程序状态寄存器(psr)。MRS指令将cpsr或spsr的内容传输到寄存器中;反过来,MSR指令将寄存器的内容传输到cpsr或spsr中。这些指令结合起来用于读写cpsr和spsr。

在语法中可以看到一个名为fields的标签。它可以是控制(c)、扩展(x)、状态(s)和标志(f)的任意组合。这些字段与psr的特定字节区域相关联,如图3.9所示。
语法:MRS{<cond>} Rd,<cpsr|spsr>
MSR{<cond>} <cpsr|spsr>_<fields>,Rm
MSR{<cond>} <cpsr|spsr>_<fields>,#immediate

c字段控制中断屏蔽、Thumb状态和处理器模式。
示例3.26展示了如何通过清除I屏蔽位来启用IRQ中断。此操作涉及使用MRS和MSR指令从cpsr读取然后写入。
示例3.26首先将cpsr复制到寄存器r1中。BIC指令清除r1的第7位。然后将寄存器r1复制回cpsr,从而启用IRQ中断。从这个示例可以看出,这段代码保留了cpsr中的所有其他设置,只修改了控制字段中的I位。
PRE
cpsr = nzcvqIFt_SVC
MRS r1, cpsr
BIC r1, r1, #0x80 ; 0b01000000
MSR cpsr_c, r1
POST
cpsr = nzcvqiFt_SVC这个示例是在SVC模式下的。在用户模式下,你可以读取cpsr的所有位,但只能更新条件标志字段f。
3.5.1 Coprocessor Instructions
协处理器指令用于扩展指令集。一个协处理器可以提供额外的计算能力,也可以用于控制内存子系统,包括高速缓存和内存管理。协处理器指令包括数据处理、寄存器传输和内存传输指令。我们只提供一个简要的概述,因为这些指令是特定于协处理器的。请注意,这些指令只被具有协处理器的核心使用。
语法:CDP{<cond>} cp, opcode1, Cd, Cn {, opcode2}
<MRC|MCR>{<cond>} cp, opcode1, Rd, Cn, Cm {, opcode2}
<LDC|STC>{<cond>} cp, Cd, addressing

在协处理器指令的语法中,cp字段表示协处理器编号,范围在p0到p15之间。opcode字段描述要在协处理器上执行的操作。Cn、Cm和Cd字段描述了协处理器内的寄存器。协处理器的操作和寄存器取决于你使用的具体协处理器。协处理器15(CP15)保留用于系统控制目的,如内存管理、写缓冲控制、缓存控制和识别寄存器。
示例3.27展示了将一个CP15寄存器复制到通用寄存器中的情况。
; transferring the contents of CP15 register c0 to register r10
MRC p15, 0, r10, c0, c0, 0在这里,CP15寄存器-0包含处理器的识别号。这个寄存器被复制到通用寄存器r10中。
3.5.2 Coprocessor 15 Instruction Syntax
CP15用于配置处理器核心,并有一组专用寄存器用于存储配置信息,如示例3.27所示。写入寄存器的值设置配置属性,例如打开缓存。
CP15被称为系统控制协处理器。MRC和MCR指令都用于读写CP15,其中寄存器Rd是核心目标寄存器,Cn是主寄存器,Cm是次级寄存器,opcode2是次级寄存器修改器。你偶尔会听到将次级寄存器称为“扩展寄存器”。
以下是将CP15控制寄存器c1的内容移动到处理器内核的寄存器r1中的指令:
MRC p15, 0, r1, c1, c0, 0
我们使用缩写符号来引用CP15,使得引用配置寄存器更易于跟踪。引用符号采用以下格式:
CP15:cX:cY:Z
第一个术语CP15将其定义为协处理器15。在分隔冒号之后的第二个术语是主寄存器。主寄存器X的值可以在0和15之间。第三个术语是次级或扩展寄存器。次级寄存器Y的值可以在0和15之间。最后一个术语opcode2是指令修改器,可以在0和7之间取值。某些操作也可能使用opcode1的非零值。我们将其写为CP15:w:cX:cY:Z。
3.6 Loading Constants
你可能已经注意到,ARM指令集中没有将32位常量移动到寄存器的直接指令。因为ARM指令的大小是32位,无法直接指定32位常量。
为了帮助编程,有两个伪指令可以将32位值移动到寄存器中。
语法:LDR Rd,=constant
ADR Rd,label

第一个伪指令使用可用的任何指令将32位常量写入寄存器。如果无法使用其他指令对常量进行编码,它会默认为内存读取操作。
第二个伪指令将相对地址写入寄存器,并使用PC相对表达式进行编码。
示例3.28
以下示例展示了一个LDR指令将32位常量0xff00ffff加载到寄存器r0中。
LDR r0, [pc, #constant_number-8-{PC}]
:
constant_number
DCD 0xff00ffff这个示例需要访问内存来加载常量,对于对时间非常敏感的程序可能会比较耗时。示例3.29展示了一种另外的方法,可以使用MVN指令将相同的常量加载到寄存器r0中。
示例3.29 使用MVN指令加载常量0xff00ffff。
PRE
none...
MVN r0, #0x00ff0000
POST
r0 = 0xff00ffff正如你所看到的,有多种替代方法可以避免访问内存,但这取决于你要加载的常量。编译器和汇编器使用巧妙的技术来避免从内存中加载常量。这些工具使用算法来找出生成寄存器中常量所需的最佳指令数量,并广泛使用移位器。如果这些方法无法生成常量,则从内存中加载。LDR伪指令将插入MOV或MVN指令来生成一个值(如果可能的话),或者生成一个带有PC相对地址的LDR指令,从字面常量池(嵌入在代码中的数据区域)中读取常量。

表3.12显示了两个伪代码转换。第一个转换生成一个简单的MOV指令;第二个转换生成一个PC相对加载指令。我们建议使用这个伪指令来加载常量。为了查看汇编器如何处理特定的加载常量,你可以通过反汇编器来传递输出,它将列出工具选择用于加载常量的指令。
另一个有用的伪指令是ADR指令,或者地址相关。该指令使用PC相对加法或减法,将给定标签的地址放入寄存器Rd中。
3.7 ARMv5E Extensions
ARMv5E扩展提供了许多新的指令(参见表3.13)。其中最重要的增强之一是对16位数据进行操作的带符号乘积累加指令。在许多ARMv5E实现中,这些操作只需要一个周期。
ARMv5E在操作16位值时提供了更大的灵活性和效率,这对于诸如16位数字音频处理等应用非常重要。
3.7.1 Count Leading Zeros Instruction
"Count Leading Zeros"(CLZ)指令用于计算从最高有效位到第一个置为1的位之间的零的数量。示例3.30展示了一个CLZ指令的示例。
示例3.30:
从这个例子中可以看出,第一个置为1的位之前有27个零。在需要对数字进行归一化的程序中,CLZ非常有用。
PRE
r1 = 0b00000000000000000000000000010000
CLZ r0, r1
POST
r0 = 273.7.2 Saturated Arithmetic
正常的ARM算术指令在整数值溢出时会进行循环。例如,0x7fffffff+1= -0x80000000。因此,在设计算法时,必须小心不要超过32位整数可表示的最大值。
示例3.31:
这个例子展示了超过最大值时会发生什么。
PRE
cpsr = nzcvqiFt_SVC
r0 = 0x00000000
r1 = 0x70000000 (positive)
r2 = 0x7fffffff (positive)
ADDS r0, r1, r2
POST
cpsr = NzcVqiFt_SVC
r0 = 0xefffffff (negative)在这个例子中,寄存器r1和r2包含正数。寄存器r2等于0x7fffffff,这是32位中可以存储的最大正值。在理想情况下,将这些数字相加应该得到一个很大的正数。然而,实际上这个值变为负数,并且溢出标志V被设置。

相比之下,使用ARMv5E指令你可以使结果饱和——一旦超过最大数值,结果将保持在0x7fffffff的最大值。这避免了需要额外的代码来检查可能的溢出的要求。表3.14列出了所有的ARMv5E饱和指令。
示例3.32: 这个例子展示了相同的数据被传递到QADD指令中。
PRE
cpsr = nzcvqiFt_SVC
r0 = 0x00000000
r1 = 0x70000000 (positive)
r2 = 0x7fffffff (positive)
QADD r0, r1, r2
POST
cpsr = nzcvQiFt_SVC
r0 = 0x7fffffff您会注意到饱和的数值返回在寄存器r0中。此外,Q位(cpsr的第27位)已被设置,表示发生了饱和。Q标志是粘滞的,直到明确清除之前都将保持设置状态。
3.7.3 ARMv5E Multiply Instructions

表3.15显示了ARMv5E乘法指令的完整列表。在表中,x和y分别选择32位寄存器中用于第一个和第二个操作数的哪16位。这些字段设置为字母T代表高16位,或字母B代表低16位。对于具有32位结果的乘加运算,Q标志指示累加是否溢出了有符号的32位值。
示例3.33: 这个例子展示了如何使用这些操作。该例使用了有符号乘积累加指令SMLATB。
PRE
r1 = 0x20000001
r2 = 0x20000001
r3 = 0x00000004
SMLATB r4, r1, r2, r3
POST
r4 = 0x00002004指令将寄存器r1的高16位与寄存器r2的低16位相乘,然后将结果加到寄存器r3中,并将最终结果写入目标寄存器r4。
3.8 Conditional Execution
大多数ARM指令都可以有条件地执行——您可以指定只有在条件码标志通过给定条件或测试时才执行指令。通过使用条件执行指令,您可以提高性能和代码密度。 条件字段是附加在指令助记符后面的两个字母缩写。默认助记符是AL,即总是执行。 条件执行减少了分支的数量,从而减少了流水线刷新的次数,从而提高了执行代码的性能。条件执行依赖于两个组件:条件字段和条件标志。条件字段位于指令中,条件标志位位于cpsr中。 示例3.34: 这个例子展示了带有EQ条件的ADD指令。只有当cpsr中的零标志被设置为1时,此指令才会被执行。
; r0 = r1 + r2 if zero flag is set
ADDEQ r0, r1, r2只有附加在助记符末尾的比较指令和带有S后缀的数据处理指令会更新cpsr中的条件标志。
示例3.35: 为了说明条件执行的优势,我们将使用这个示例中显示的简单C代码片段,并比较使用非条件和条件指令的汇编输出。
while (a!=b)
{
if (a>b) a -= b; else b -= a;
}让寄存器r1表示a,寄存器r2表示b。下面的代码片段展示了相同算法的ARM汇编版本。这个示例只在分支指令上使用条件执行。
; Greatest Common Divisor Algorithm
gcd
CMP r1, r2
BEQ complete
BLT lessthan
SUB r1, r1, r2
B gcd
lessthan
SUB r2, r2, r1
B gcd
complete
...现在让我们将代码与完全条件执行的版本进行比较。正如您所看到的,这显著减少了指令的数量:
3.9 Summary
本章介绍了ARM指令集。所有的ARM指令长度都是32位。算术、逻辑、比较和移动指令都可以使用内联桶移位器,在第二个寄存器Rm输入ALU之前进行预处理。
ARM指令集有三种类型的载入-存储指令:单寄存器载入-存储、多寄存器载入-存储和交换。多载入-存储指令提供了对栈进行推入-弹出操作的功能。ARM-Thumb过程调用标准(ATPCS)将栈定义为一个完全降序的堆栈。
软件中断指令触发一个软件中断,将处理器强制置于SVC模式;该指令调用特权操作系统例程。程序状态寄存器指令用于写入和读取cpsr和spsr。还有一些特殊的伪指令,优化32位常数的加载。
ARMv5E扩展包括前导零计数、饱和和改进的乘法指令。前导零计数指令计算第一个二进制一之前的二进制零的数量。饱和处理超出32位整数值的算术计算。改进的乘法指令提供更好的灵活性,可以用于乘法16位值的操作。
大多数ARM指令都可以有条件地执行,这可以显著减少执行特定算法所需的指令数量。
Chapter4 Introduction to the Thumb Instruction Set
本章介绍了Thumb指令集。Thumb将32位ARM指令的子集编码为16位指令集空间。由于在具有16位数据总线的处理器上,Thumb性能优于ARM,但在32位数据总线上性能低于ARM,因此在内存受限的系统中使用Thumb。
Thumb具有更高的代码密度,即可执行程序在内存中占用的空间比ARM少。对于内存受限的嵌入式系统,例如移动电话和个人数码助理(PDA),代码密度非常重要。成本压力还限制了内存大小、宽度和速度。

平均而言,相同代码的Thumb实现占用的内存量比等效的ARM实现少约30%。例如,图4.1展示了在ARM和Thumb汇编代码中实现的相同除法代码例程。尽管Thumb实现使用了更多指令,但整体内存占用减少了。
代码密度是推动Thumb指令集开发的主要动力。由于它也被设计为编译器的目标,而不是手写汇编代码的目标,我们建议您使用高级语言(如C或C++)编写针对Thumb的代码。


每个Thumb指令与一个32位ARM指令相关。图4.2显示了简单的Thumb ADD指令如何解码为等效的ARM ADD指令。表4.1提供了在ARMv5TE架构中使用的THUMBv2架构中可用的完整Thumb指令列表。只有相对分支指令可以有条件地执行。16位中有限的空间导致Thumb ISA中的桶移位操作ASR、LSL、LSR和ROR成为单独的指令。
本章只描述了这些指令的一个子集,因为大多数代码都是从高级语言编译而来的。请参考附录A获取Thumb指令的完整列表。
本章涵盖了Thumb寄存器的使用、ARM-Thumb互操作、分支指令、数据处理指令、加载存储指令、堆栈操作和软件中断。
4.1 Thumb Register Usage

在Thumb状态下,您无法直接访问所有寄存器。只有低位寄存器r0到r7是完全可访问的,如表4.2所示。较高的寄存器r8到r12只能通过MOV、ADD或CMP指令进行访问。CMP和所有操作低位寄存器的数据处理指令会更新cpsr中的条件标志。
您可能已经从Thumb指令集列表和Thumb寄存器使用表中注意到,没有直接访问cpsr或spsr的方式。换句话说,Thumb指令集中没有等效于MSR和MRS的指令。
要更改cpsr或spsr,您必须切换到ARM状态使用MSR和MRS指令。同样,在Thumb状态下也没有协处理器指令。您需要进入ARM状态才能访问协处理器,以配置缓存和内存管理。
4.2 ARM-Thumb Interworking
ARM-Thumb互操作是将ARM和Thumb代码链接在一起的方法,适用于汇编语言和C/C++。它处理两种状态之间的转换。有时需要额外的代码(称为veneer)来执行状态转换。ATPCS定义了ARM和Thumb过程调用标准。
要从ARM例程调用Thumb例程,核心必须改变状态。这个状态改变显示在cpsr的T位上。BX和BLX分支指令在跳转到例程时引发ARM和Thumb状态之间的切换。BX lr指令也会返回例程,并在必要时进行状态切换。
BLX指令是在ARMv5T中引入的。在ARMv4T核心上,链接器在子例程调用时使用一个veneer来进行状态切换。链接器不直接调用例程,而是调用veneer,veneer使用BX指令切换到Thumb状态。
BX或BLX指令有两个版本:一个是ARM指令,另一个是Thumb指令。ARM BX指令只在Rn中的地址的第0位设置为二进制1时进入Thumb状态;否则进入ARM状态。Thumb BX指令执行相同的操作。
语法:BX Rm
BLX Rm | label

不同于ARM版本,Thumb BX指令无法按条件执行。
示例4.1:
这个示例展示了一个小的代码片段,使用了ARM和Thumb版本的BX指令。可以看到,跳转到Thumb的分支地址的最低位被设置为1,这将在cpsr中的T位上将状态设置为Thumb状态。
返回地址不会自动由BX指令保留。相反,代码在分支之前使用MOV指令显式地设置返回地址。
; ARM code
CODE32
; word aligned
LDR r0, =thumbCode+1 ; +1 to enter Thumb state
MOV lr, pc
; set the return address
BX r0
; branch to Thumb code & mode
; continue here
; Thumb code
CODE16
; halfword aligned
thumbCode
ADD r1, #1
BX lr
; return to ARM code & state一个分支交换指令也可以作为绝对分支使用,只要不使用第0位来强制状态变化即可:
; address(thumbCode) = 0x00010000
; cpsr = nzcvqIFt_SVC
; r0 = 0x00000000
0x00009000 LDR r0, =thumbCode+1
; cpsr = nzcvqIFt_SVC
; r0 = 0x00010001
0x00009008 BX r0
; cpsr = nzcvqIFT_SVC
; r0 = 0x00010001
; pc = 0x00010000可以看到,寄存器r0的最低有效位被用于设置cpsr中的T位。在执行BX指令之前,cpsr从IFt状态变为IFT状态。然后,将pc设置为指向Thumb例程的起始地址。
示例4.2:
通过将BX指令替换为BLX指令,可以简化对Thumb例程的调用,因为它会在链接寄存器lr中设置返回地址。
CODE32
LDR r0, =thumbRoutine+1 ; enter Thumb state
BLX r0
; jump to Thumb code
; continue here
CODE16
thumbRoutine
ADD r1, #1
BX r14
; return to ARM code and state4.3 Other Branch Instructions
有两种标准分支指令或B的变体。第一种类似于ARM版本,并且可以按条件执行;分支范围限制在有符号的8位立即数,即-256到+254字节之间。第二种版本去除了指令的条件部分,并将有效的分支范围扩展为有符号的11位立即数,即-2048到+2046字节之间。
条件分支指令是Thumb状态下唯一可以按条件执行的指令。
语法:
B<cond> label
B label
BL label

BL指令不是按条件执行的,并且具有约±4MB的近似范围。之所以有这个范围,是因为BL(和BLX)指令被转换成一对16位的Thumb指令。该对指令中的第一条指令保存分支偏移的高位,第二条指令保存低位。这些指令必须成对使用。
下面的代码展示了从BL子程序调用中返回所使用的各种指令:

要进行返回操作,我们将pc设置为lr中保存的值。关于栈指令POP的详细讨论将在第4.7节中进行。
4.4 Data Processing Instructions
数据处理指令用于在寄存器内操作数据。它们包括移动指令、算术指令、移位指令、逻辑指令、比较指令和乘法指令。Thumb数据处理指令是ARM数据处理指令的一个子集。
语法:
<ADC|ADD|AND|BIC|EOR|MOV|MUL|MVN|NEG|ORR|SBC|SUB> Rd, Rm
<ADD|ASR|LSL|LSR|ROR|SUB> Rd, Rn #立即数
<ADD|MOV|SUB> Rd,#立即数
<ADD|SUB> Rd,Rn,Rm
ADD Rd,pc,#立即数
ADD Rd,sp,#立即数
<ADD|SUB> sp, #立即数
<ASR|LSL|LSR|ROR> Rd,Rs
<CMN|CMP|TST> Rn,Rm
CMP Rn,#立即数
MOV Rd,Rn


这些指令的风格与相应的ARM指令相同。大多数Thumb数据处理指令操作低寄存器并更新cpsr。异常情况包括:
MOV Rd,Rn
ADD Rd,Rm
CMP Rn,Rm
ADD sp, #立即数
SUB sp, #立即数
ADD Rd,sp,#立即数
ADD Rd,pc,#立即数
它们可以在高寄存器r8-r14和pc上进行操作,但使用高寄存器时这些指令除了CMP外不会更新cpsr中的条件标志位。然而,CMP指令总是更新cpsr。
示例4.3
以下示例展示了一个简单的Thumb ADD指令。它将两个低寄存器r1和r2相加,然后将结果放入寄存器r0中,覆盖原始内容。同时也会更新cpsr。
PRE
cpsr = nzcvIFT_SVC
r1 = 0x80000000
r2 = 0x10000000
ADD r0, r1, r2
POST
r0 = 0x90000000
cpsr = NzcvIFT_SVC示例4.4
Thumb与ARM风格不同之处在于位移操作(ASR,LSL,LSR和ROR)是单独的指令。这个示例展示了逻辑左移(LSL)指令,用于将寄存器r2乘以2。
PRE
r2 = 0x00000002
r4 = 0x00000001
LSL r2, r4
POST
r2 = 0x00000004
r4 = 0x00000001请查看附录A,获取完整的Thumb数据处理指令列表。
4.5 Single-Register Load-Store Instructions
Thumb指令集支持加载和存储寄存器,即LDR和STR指令。这些指令使用两种预索引寻址模式:寄存器偏移和立即数偏移。
语法: <LDR|STR>{<B|H>} Rd, [Rn,#立即数]
LDR{<H|SB|SH>} Rd,[Rn,Rm]
STR{<B|H>} Rd,[Rn,Rm]
LDR Rd,[pc,#立即数]
<LDR|STR> Rd,[sp,#立即数]


在表4.3中可以看到不同的寻址模式。寄存器偏移使用基础寄存器Rn加上寄存器偏移量Rm。第二种方式使用相同的基础寄存器Rn加上一个5位立即数,或者一个与数据大小相关的值。指令中编码的5位偏移量对于字节访问乘以1,对于16位访问乘以2,对于32位访问乘以4。
示例4.5
这个示例展示了两个使用预索引寻址模式的Thumb指令。两者都使用相同的前提条件。
PRE
mem32[0x90000] = 0x00000001
mem32[0x90004] = 0x00000002
mem32[0x90008] = 0x00000003
r0 = 0x00000000
r1 = 0x00090000
r4 = 0x00000004
LDR r0, [r1, r4] ; register
POST r0 = 0x00000002
r1 = 0x00090000
r4 = 0x00000004
LDR r0, [r1, #0x4] ; immediate
POST r0 = 0x00000002这两个指令执行相同的操作,唯一的区别在于第二个LDR指令使用一个固定的偏移量,而第一个LDR指令依赖于寄存器r4中的值。
4.6 Multiple-Register Load-Store Instructions
Thumb版本的加载存储多个指令是ARM加载存储多个指令的简化形式。它们只支持增量后(IA)寻址模式。
语法: <LDM|STM>IA Rn!, {低位寄存器列表}

这里的N是寄存器列表中寄存器的数量。可以看到,这些指令在执行后总是更新基址寄存器Rn。基址寄存器和寄存器列表仅限于低位寄存器r0到r7。
例如,在以下示例4.6中,将寄存器r1到r3保存到内存地址0x9000到0x900c中,并更新基址寄存器r4。需要注意的是,与ARM指令集不同,更新符号!不是一个选项。
PRE
r1 = 0x00000001
r2 = 0x00000002
r3 = 0x00000003
r4 = 0x9000
STMIA r4!,{r1,r2,r3}
POST
mem32[0x9000] = 0x00000001
mem32[0x9004] = 0x00000002
mem32[0x9008] = 0x00000003
r4 = 0x900c4.7 Stack Instructions
Thumb堆栈操作与对应的ARM指令不同,因为它们使用更传统的POP和PUSH概念。
语法:POP {低位寄存器列表{, pc}}
PUSH {低位寄存器列表{, lr}}

值得注意的一点是,在指令中没有堆栈指针。这是因为在Thumb操作中,堆栈指针固定为寄存器13,并且sp会自动更新。寄存器列表仅限于低位寄存器r0到r7。
PUSH寄存器列表也可以包括链接寄存器lr;同样,POP寄存器列表也可以包括程序计数器pc。这为子例程的进入和退出提供了支持,如示例4.7所示。
堆栈指令仅支持完全下降的堆栈操作。
示例4.7
在这个例子中,我们使用了POP和PUSH指令。使用带链接的分支(BL)指令调用了子例程ThumbRoutine。
; Call subroutine
BL ThumbRoutine
; continue
ThumbRoutine
PUSH {r1, lr} ; enter subroutine
MOV r0, #2
POP {r1, pc} ; return from subroutine链接寄存器lr与寄存器r1一起被推入堆栈中。在返回时,寄存器r1从堆栈中弹出,同时返回地址被加载到pc寄存器中。这样就从子例程中返回了。
4.8 Software Interrupt Instruction
与ARM等效指令类似,Thumb软件中断(SWI)指令会引发一个软件中断异常。如果在Thumb状态下引发了任何中断或异常标志,处理器会自动返回到ARM状态以处理异常。
语法:SWI immediate

Thumb SWI指令与ARM等效指令具有相同的效果和几乎相同的语法。不同之处在于SWI编号的范围限制为0到255,并且不会有条件地执行。
示例4.8
这个例子展示了执行Thumb SWI指令的过程。请注意,在执行后,处理器从Thumb状态切换到ARM状态。
PRE
cpsr = nzcVqifT_USER
pc = 0x00008000
lr = 0x003fffff ; lr = r14
r0 = 0x12
0x00008000 SWI 0x45
POST
cpsr = nzcVqIft_SVC
spsr = nzcVqifT_USER
pc = 0x00000008
lr = 0x00008002
r0 = 0x124.9 Summary
在本章中,我们介绍了Thumb指令集。所有Thumb指令的长度都为16位。相比于ARM代码,Thumb提供了约30%的代码密度优势。大多数用于Thumb编写的代码是使用高级语言如C和C++编写的。
ATPCS定义了ARM和Thumb代码之间的调用方式,称为ARM-Thumb交互操作。交互操作使用分支交换(BX)指令和带链接的分支交换(BLX)指令来改变状态并跳转到特定的例程。
在Thumb中,只有分支指令具有条件执行的能力。移位操作(ASR、LSL、LSR和ROR)是单独的指令。
多寄存器加载/存储指令仅支持递增后(IA)寻址模式。Thumb指令集包含了作为堆栈操作的POP和PUSH指令。这些指令只支持完全下降的堆栈操作。
Thumb指令集中没有用于访问协处理器、cpsr和spsr的指令。
Chapter5 Efficient C Programming
本章的目的是帮助您以一种在ARM架构上编译高效的方式编写C代码。我们将通过许多小例子来展示编译器如何将C源代码转换为ARM汇编代码。一旦您了解了这个转换过程,就能够区分快速的C代码和慢速的C代码。这些技术同样适用于C++,但在这些例子中我们将专注于纯C。
我们首先概述C编译器和优化,这将让您了解C编译器在优化代码时面临的问题。通过理解这些问题,您可以编写更高效的源代码,提高速度并减小代码大小。下面的小节按主题进行分组。
第5.2节和第5.3节介绍了如何优化基本的C循环。这些节以数据包校验和作为简单的示例来说明相关思想。第5.4节和第5.5节介绍了如何优化整个C函数体,包括编译器如何在函数内分配寄存器以及如何减少函数调用的开销。
第5.6节到第5.9节探讨了与内存相关的问题,包括处理指针以及如何高效地压缩数据和访问内存。第5.10节到第5.12节介绍了通常不直接由ARM指令支持的基本操作。您可以使用内联函数和汇编语言来添加自己的基本操作。
最后一节总结了在将C代码从其他架构移植到ARM架构时可能遇到的问题。
5.1 Overview of C Compilers and Optimization
本章假设您熟悉C语言并具有一定的汇编程序设计知识。后者并非必需,但对于跟踪编译器输出示例很有用。有关ARM汇编语法的详细信息,请参见第三章或附录A。
优化代码需要时间并降低源代码的可读性。通常,只有经常执行且对性能至关重要的函数值得优化。我们建议您使用大多数ARM模拟器中都有的性能分析工具来查找这些经常执行的函数。使用源代码注释来记录不明显的优化以帮助可维护性。
C编译器必须按照字面意义将您的C函数转换为汇编语言,以便其适用于所有可能的输入。实际上,许多输入组合是不可能的或不会发生的。让我们从一个例子开始,看看编译器面临的问题。memclr函数清除地址为data的N个字节的内存。
void memclr(char *data, int N)
{
for (; N>0; N--)
{
*data=0;
data++;
}
}无论编译器有多先进,它都不知道N在输入时是否可能为0。因此,在循环的第一次迭代之前,编译器需要显式地测试这种情况。
编译器不知道data数组指针是否是四字节对齐的。如果它是四字节对齐的,则编译器可以使用int存储而不是char存储一次清除四个字节。编译器也不知道N是否是四的倍数。如果N是四的倍数,则编译器可以重复循环体四次或一次存储四个字节。
编译器必须保守,并假设N的所有可能值以及data的所有可能对齐方式。第5.3节详细讨论了这些具体点。
要编写高效的C代码,您必须了解C编译器必须保守的区域,C编译器正在映射的处理器架构的限制,以及特定C编译器的限制。
本章大部分内容涵盖了上述前两点,并适用于任何ARM C编译器。第三点将非常依赖于编译器供应商和编译器版本。您需要查看编译器的文档或自己进行实验。
为了使我们的示例具体化,我们使用以下特定的C编译器进行了测试:
■ ARM Developer Suite版本1.1 (ADS1.1) 的 armcc。您可以直接从ARM许可该编译器或其后续版本。
■ arm-elf-gcc 版本2.95.2。这是GNU C编译器(gcc)的ARM目标,可以免费获取。
我们使用来自ADS1.1的armcc来生成本书中示例的汇编输出。以下简短的脚本演示了如何在C文件test.c上调用armcc。您可以使用此脚本来复现我们的示例。
armcc -Otime -c -o test.o test.c
fromelf -text/c test.o > test.txt
默认情况下,armcc开启了全部优化(-O2命令行开关)。-Otime开关针对执行效率进行优化,而不是空间优化,主要影响for和while循环的布局。如果您使用gcc编译器,则以下简短的脚本将生成类似的汇编输出列表:
arm-elf-gcc -O2 -fomit-frame-pointer -c -o test.o test.c
arm-elf-objdump -d test.o > test.txt
默认情况下,GNU编译器关闭了全部优化。-fomit-frame-pointer开关会阻止GNU编译器维护帧指针寄存器。帧指针有助于通过指向存储在堆栈帧上的局部变量来调试查看。然而,它们在维护方面效率低下,并且不应该在对性能至关重要的代码中使用。
5.2 Basic C Data Types
让我们首先看一下ARM编译器如何处理基本的C数据类型。我们将会发现,某些类型在用于局部变量时更为高效。在加载和存储每种类型的数据时,也存在着不同的寻址模式。
ARM处理器拥有32位寄存器和32位数据处理操作。ARM架构是一种RISC(精简指令集计算机)加载/存储架构。换句话说,在对数据进行操作之前,您必须将其从内存加载到寄存器中。没有直接操作内存中的算术或逻辑指令。
早期版本的ARM架构(ARMv1到ARMv3)提供了对加载和存储无符号8位和无符号或有符号32位值的硬件支持。
//ARMv8现在支持64位寄存器了吧?
//是的,ARMv8架构引入了64位寄存器,使得ARM处理器能够处理更大范围的数据和更复杂的计算任务。ARMv8架构是一个64位的RISC架构,提供了对64位数据的原生支持,同时还能够向下兼容32位指令集。这使得ARMv8处理器在处理大规模数据和高性能计算方面表现出色。

这些架构用于在ARM7TDMI之前的处理器上。表5.1显示了按照ARM架构可用的加载/存储指令类别。
在表5.1中,对8位或16位值进行加载操作时,在写入ARM寄存器之前会将该值扩展为32位。无符号值会进行零扩展,有符号值会进行符号扩展。这意味着将加载的值强制转换为int类型不会产生额外的指令。类似地,存储8位或16位值时,会选择寄存器的最低8位或16位。将int类型强制转换为较小类型在存储过程中也不会增加额外的指令。
从ARMv4架构开始,通过新增的指令,ARMv4及以上版本的架构直接支持有符号8位和16位的加载和存储。由于这些指令是后来添加的,因此其支持的寻址模式不如早期的ARMv4指令多。(有关不同寻址模式的详细信息,请参见第3.3节。)我们将在第5.2.1节的示例checksum_v3中看到这种影响。
最后,ARMv5增加了对64位加载和存储的指令支持。这在ARM9E和后续的核心中可用。
在ARMv4之前,ARM处理器在处理有符号8位或任何16位值时效果不佳。因此,ARM C编译器将char定义为无符号8位值,而不是像许多其他编译器那样定义为有符号8位值。

编译器armcc和gcc在ARM目标上使用表5.2中的数据类型映射。值得注意的是char类型的特殊情况,当你将代码从另一种处理器架构移植时,可能会遇到问题。常见的示例是将char类型变量i用作循环计数器,并使用循环继续条件i ≥ 0。由于对于ARM编译器来说,i是无符号的,因此循环永远不会终止。幸运的是,armcc在这种情况下会产生一个警告:unsigned comparison with 0。编译器还提供了一个覆盖开关来将char定义为有符号类型。例如,gcc的命令行选项-fsigned-char将char定义为有符号类型。以下命令行选项-armcc的-zc将产生相同的效果。
在本书的其余部分,我们假设您正在使用ARMv4处理器或更高版本。这包括ARM7TDMI和所有后续处理器。
5.2.1 Local Variable Types
基于ARMv4的处理器可以高效地加载和存储8位、16位和32位数据。然而,大部分ARM数据处理操作仅支持32位。因此,应在可能的情况下使用32位数据类型int或long作为本地变量类型。即使您正在处理8位或16位值,也应避免使用char和short作为本地变量类型。唯一的例外是当您想要出现环绕效果时。如果需要形如255 + 1 = 0的模运算,则使用char类型。
为了了解本地变量类型的影响,我们可以考虑一个简单的例子。我们将详细介绍一种校验和函数,该函数对数据包中的值进行求和。大多数通信协议(如TCP/IP)都有校验和或循环冗余校验(CRC)例程,以检查数据包中的错误。
以下代码计算一个包含64个字的数据包的校验和。它展示了为什么应避免在本地变量中使用char。
int checksum_v1(int *data)
{
char i;
int sum = 0;
for (i = 0; i < 64; i++)
{
sum += data[i];
}
return sum;
}乍一看,将i声明为char类型似乎是有效的。您可能认为char类型在ARM寄存器空间或堆栈空间上使用的空间比int类型少。然而,在ARM上,这两种假设都是错误的。所有ARM寄存器都是32位,并且所有堆栈条目至少是32位。此外,为了确切实现i++操作,编译器必须考虑i等于255的情况。任何尝试递增255都应该得到答案0。
请考虑此函数的编译器输出。我们已添加标签和注释以使汇编代码更清晰。
checksum_v1
MOV r2,r0
; r2 = data
MOV r0,#0
; sum = 0
MOV r1,#0
;i=0
checksum_v1_loop
LDR r3,[r2,r1,LSL #2] ; r3 = data[i]
ADD r1,r1,#1
; r1 = i+1
AND r1,r1,#0xff ; i = (char)r1
CMP r1,#0x40
; compare i, 64
ADD r0,r3,r0
; sum += r3
BCC checksum_v1_loop ; if (i<64) loop
MOV pc,r14
; return sum现在来将这与将i声明为无符号整数(unsigned int)的编译器输出进行比较。
checksum_v2
MOV r2,r0
; r2 = data
MOV r0,#0
; sum = 0
MOV r1,#0
;i=0
checksum_v2_loop
LDR r3,[r2,r1,LSL #2] ; r3 = data[i]
ADD r1,r1,#1
; r1++
CMP r1,#0x40
; compare i, 64
ADD r0,r3,r0
; sum += r3
BCC checksum_v2_loop ; if (i<64) goto loop
MOV pc,r14
; return sum在第一种情况下,编译器会插入额外的AND指令,将i缩小到0到255的范围,然后再与64进行比较。而在第二种情况下,这个指令会消失。
接下来,假设数据包包含16位值并且我们需要一个16位的校验和。下面的C代码可能会让人心动:
short checksum_v3(short *data)
{
unsigned int i;
short sum = 0;
for (i = 0; i < 64; i++)
{
sum = (short)(sum + data[i]);
}
return sum;
}您可能想知道为什么for循环体中没有包含代码sum += data[i]。如果您使用编译器开关-W + n启用隐式窄化转换警告,这段代码在armcc中将产生一个警告。表达式sum + data[i]是一个整数,因此只能使用(隐式或显式)窄化转换将其赋值给short类型。正如您在以下的汇编输出中所看到的,编译器必须插入额外的指令来实现窄化转换:
checksum_v3
MOV r2,r0
; r2 = data
MOV r0,#0
; sum = 0
MOV r1,#0
;i=0
checksum_v3_loop
ADD r3,r2,r1,LSL #1 ; r3 = &data[i]
LDRH r3,[r3,#0] ; r3 = data[i]
ADD r1,r1,#1
; i++
CMP r1,#0x40
; compare i, 64
ADD r0,r3,r0
; r0 = sum + r3
MOV r0,r0,LSL #16
MOV r0,r0,ASR #16 ; sum = (short)r0
BCC checksum_v3_loop ; if (i<64) goto loop
MOV pc,r14
; return sum现在,这个循环比之前的checksum_v2的循环多了三个指令!这些额外指令有两个原因:
■ LDRH指令不允许使用移位地址偏移量,而之前的checksum_v2中LDR指令允许。因此,循环中的第一个ADD计算了数组中项i的地址。LDRH从没有偏移量的地址加载数据。LDRH的寻址模式比LDR少,因为它是ARM指令集的后期添加。(见5.1表)
■ 将total + array[i]转换为short类型需要两个MOV指令。编译器左移16位,然后右移16位来实现16位的符号扩展。右移是一种符号扩展移位,因此它将符号位复制到高16位以填充它们。
我们可以通过使用int类型变量来保存部分求和来避免第二个问题。我们只在函数退出时将总和缩小为short类型。
然而,第一个问题是一个新的问题。我们可以通过递增指针data来访问数组,而不是像data[i]那样使用索引来解决它。这种方式无论数组类型大小或元素大小都是高效的。所有的ARM加载和存储指令都有后增加寻址模式。
示例5.1中的checksum_v4代码修复了我们在本节中讨论的所有问题。它使用int类型的局部变量来避免不必要的转换。它递增指针data,而不是使用索引偏移data[i]。
short checksum_v4(short *data)
{
unsigned int i;
int sum=0;
for (i=0; i<64; i++)
{
sum += *(data++);
}
return (short)sum;
}*(data++)操作转换为一个ARM指令,该指令加载数据并递增数据指针。当然,您也可以编写sum += *data; data++;或者*data++,如果您喜欢的话。编译器产生以下输出。与checksum_v3相比,内部循环中删除了三个指令,每个循环节省三个周期。
checksum_v4
MOV r2,#0
; sum = 0
MOV r1,#0
;i=0
checksum_v4_loop
LDRSH r3,[r0],#2 ; r3 = *(data++)
ADD r1,r1,#1
; i++
CMP r1,#0x40
; compare i, 64
ADD r2,r3,r2
; sum += r3
BCC checksum_v4_loop ; if (sum<64) goto loop
MOV r0,r2,LSL #16
MOV r0,r0,ASR #16 ; r0 = (short)sum
MOV pc,r14
; return r0编译器仍然在函数返回时执行一次将结果转换为16位范围的操作。您可以根据5.2.2节中的讨论,通过返回一个int类型的结果来消除这个转换。
5.2.2 Function Argument Types
我们在5.2.1节中看到,将局部变量从char或short类型转换为int类型可以提高性能并减小代码大小。对于函数参数也是一样的。考虑下面这个简单的函数,它将两个16位的值相加,将第二个值除以2,然后返回一个16位的和:
short add_v1(short a, short b)
{
return a + (b >> 1);
}这个函数可能有些虚构,但它是一个有用的测试用例,可以说明编译器面临的问题。输入值a、b和返回值将被传递到32位ARM寄存器中。编译器应该假设这些32位值在short类型的范围内,即-32,768到+32,767吗?还是应该通过将最低16位进行符号扩展来填充32位寄存器,强制将值限制在这个范围内?编译器必须为函数的调用者和被调用者做出兼容的决策。调用者或被调用者必须执行到short类型的转换。
我们说函数参数是“宽”的,如果它们没有缩小到类型的范围内;如果它们已经缩小到范围内,则称其为“窄”。您可以通过查看add_v1的汇编输出来了解编译器所做的决策。如果编译器以宽的方式传递参数,那么被调用者必须将函数参数缩小到正确的范围内。如果编译器以窄的方式传递参数,那么调用者必须缩小范围。如果编译器返回宽值,则调用者必须将返回值缩小到正确的范围内。如果编译器返回窄值,则被调用者必须在返回值之前将范围缩小。
对于ADS中的armcc编译器,函数参数是窄传递的,返回值也是窄的。换句话说,调用者进行参数的转换,被调用者进行返回值的转换。编译器使用函数的ANSI原型来确定函数参数的数据类型。
add_v1的armcc输出显示,编译器将返回值转换为short类型,但没有对输入值进行转换。它假设调用者已经确保32位值r0和r1在short类型的范围内。这显示了参数和返回值的窄传递。
add_v1
ADD r0,r0,r1,ASR #1 ; r0 = (int)a + ((int)b >> 1)
MOV r0,r0,LSL #16
MOV r0,r0,ASR #16 ; r0 = (short)r0
MOV pc,r14
; return r0我们使用的gcc编译器更为谨慎,不对参数值的范围做任何假设。这个版本的编译器在调用者和被调用者中都将输入参数缩小到short类型的范围内。它还将返回值转换为short类型。以下是add_v1的编译代码示例:
add_v1_gcc
MOV r0, r0, LSL #16
MOV r1, r1, LSL #16
MOV r1, r1, ASR #17 ; r1 = (int)b >> 1
ADD r1, r1, r0, ASR #16 ; r1 += (int)a
MOV r1, r1, LSL #16
MOV r0, r1, ASR #16 ; r0 = (short)r1
MOV pc, lr
; return r0不论窄调用协议和宽调用协议有什么优劣,你可以看到char或short类型的函数参数和返回值会引入额外的转换。这会增加代码大小并降低性能。即使你只传递一个8位的值,使用int类型作为函数参数和返回值也更高效。
5.2.3 Signed versus Unsigned Types
前面的章节展示了在局部变量和函数参数中使用int类型而不是char或short类型的优点。接下来这一节将比较有符号整数和无符号整数的效率。
如果你的代码使用加、减和乘法,那么有符号和无符号操作之间没有性能差异。但是,在进行除法运算时存在差异。考虑以下简短的示例,用于计算两个整数的平均值:
int average_v1(int a, int b)
{
return (a+b)/2;
}This compiles to
average_v1
ADD r0,r0,r1 ; r0=a+b
ADD r0,r0,r0,LSR #31 ; if (r0<0) r0++
MOV r0,r0,ASR #1 ; r0 = r0 >> 1
MOV pc,r14 ; return r0请注意,如果sum是负数,编译器在右移之前会将sum加一。换句话说,它用以下语句替换了x/2的操作:
(x < 0) ? ((x + 1) >> 1) : (x >> 1)
这是因为x是有符号的。在ARM目标上的C语言中,如果x是负数,除以2并不等同于右移操作。例如,-3 >> 1 = -2,但是-3/2 = -1。除法向零取整,而算术右移则向-∞取整。
对于除法运算来说,使用无符号类型更高效。编译器会直接将无符号的2的幂次方除法转换为右移操作。对于一般的除法,C库中的除法函数对于无符号类型更快。参见第5.10节,讨论如何完全避免除法运算。
总结:高效使用C类型
• 对于存储在寄存器中的局部变量,除非需要8位或16位模运算,否则不要使用char或short类型。使用有符号或无符号int类型。在进行除法运算时,使用无符号类型更快。
• 对于存储在主存中的数组元素和全局变量,请使用尽可能小的类型来存储所需的数据。这可以节省内存空间。ARMv4架构有效地加载和存储所有数据宽度,只要您通过递增数组指针遍历数组即可。避免在short类型数组中使用从数组基地址开始的偏移量,因为LDRH指令不支持此操作。
• 在将数组元素或全局变量读入局部变量或将局部变量写入数组元素时,请使用显式转换。这样可以清楚地表明,为了快速操作,您正在将存储在内存中的窄类型扩展为寄存器中的宽类型。在编译器中开启隐式窄化转换警告以检测隐式转换。
• 避免在表达式中使用隐式或显式的窄化转换,因为它们通常会增加额外的周期。加载或存储时的强制转换通常是免费的,因为加载或存储指令会为您执行转换。
• 避免在函数参数或返回值中使用char和short类型。即使参数的范围较小,也请使用int类型。这可以防止编译器执行不必要的转换。
5.3 C Looping Structures
本节介绍在ARM上编写for循环和while循环的最高效方法。我们首先看一下具有固定迭代次数的循环,然后转向具有可变迭代次数的循环。最后我们看一下循环展开。
5.3.1 Loops with a Fixed Number of Iterations
在ARM上编写for循环最高效的方式是什么?让我们回到checksum例子,并查看循环结构。
下面是我们在第5.2节学习过的64字节数据包校验和程序的最新版本。这个例子展示了编译器如何处理一个带有递增计数i++的循环。
int checksum_v5(int *data)
{
unsigned int i;
int sum=0;
for (i=0; i<64; i++)
{
sum += *(data++);
}
return sum;
}This compiles to
checksum_v5
MOV r2,r0
; r2 = data
MOV r0,#0
; sum = 0
MOV r1,#0
;i=0
checksum_v5_loop
LDR r3,[r2],#4 ; r3 = *(data++)
ADD r1,r1,#1
; i++
CMP r1,#0x40
; compare i, 64
ADD r0,r3,r0
; sum += r3
BCC checksum_v5_loop ; if (i<64) goto loop
MOV pc,r14
; return sum在ARM上实现for循环结构通常需要三条指令:
* 使用ADD指令来增加i的值
* 使用比较指令来判断i是否小于64
* 使用条件分支指令如果i < 64,则继续执行循环
然而,这并不高效。在ARM上,循环应该只使用两条指令:
* 使用减法指令来递减循环计数器,并根据结果设置条件码标志位(condition code flags)
* 使用条件分支指令
关键是循环计数器应该按照递减到零的方式进行计数,而不是递增到任意限制值。这样,与零进行比较是免费的,因为结果存储在条件码标志位中。由于我们不再将i用作数组索引,因此按照递减计数没有问题。
下面的示例5.2展示了如果我们将循环由递增改为递减,可以获得的改进效果。
int checksum_v6(int *data)
{
unsigned int i;
int sum=0;
for (i=64; i!=0; i--)
{
sum += *(data++);
}
return sum;
}This compiles to
checksum_v6
MOV r2,r0
; r2 = data
MOV r0,#0
; sum = 0
MOV r1,#0x40
; i = 64
checksum_v6_loop
LDR r3,[r2],#4 ; r3 = *(data++)
SUBS r1,r1,#1
; i-- and set flags
ADD r0,r3,r0
; sum += r3
BNE checksum_v6_loop ; if (i!=0) goto loop
MOV pc,r14
; return sumSUBS和BNE指令实现了循环。我们的校验和示例现在每个循环只有最少的四条指令。这比校验和_v1的六条指令和校验和_v3的八条指令要好得多。
对于无符号循环计数器i,我们可以使用循环继续条件i!=0或i>0的任意一种。由于i不能为负数,它们是等价的条件。对于有符号循环计数器,人们常常倾向于使用条件i>0来继续循环。你可能会期望编译器生成以下两条指令来实现循环:
SUBS r1,r1,#1 ; compare i with 1, i=i-1
BGT loop ; if (i+1>1) goto loopIn fact, the compiler will generate
SUB r1,r1,#1 ; i--
CMP r1,#0 ; compare i with 0
BGT loop
; if (i>0) goto loop编译器并非效率低下。它必须对i = -0x80000000的情况进行特殊处理,因为在这种情况下,两段代码生成的结果是不同的。
对于第一段代码,SUBS指令将i与1进行比较,然后递减i。由于-0x80000000 < 1,循环终止。而对于第二段代码,我们先递减i,然后再与0进行比较。由于模运算的原因,i现在的值为+0x7fffffff,大于零。因此,循环会持续多次迭代。
当然,在实际应用中,i很少会取到-0x80000000这个值。编译器通常无法确定这一点,尤其是如果循环从可变次数开始(参见第5.3.2节)。
因此,对于有符号或无符号的循环计数器,你应该使用终止条件i!=0。相比于有符号i的条件i>0,它可以节省一条指令。
5.3.2 Loops Using a Variable Number of Iterations
现在假设我们希望校验和例程能够处理任意大小的数据包。我们传入一个变量N,表示数据包中的字(word)数。借鉴上一节的经验,我们会倒数计数直到N = 0,并且不需要额外的循环计数器i。
校验和_v7示例展示了编译器如何处理具有可变迭代次数N的for循环。
int checksum_v7(int *data, unsigned int N)
{
int sum=0;
for (; N!=0; N--)
{
sum += *(data++);
}
return sum;
}This compiles to
checksum_v7
MOV r2,#0
; sum = 0
CMP r1,#0
; compare N, 0
BEQ checksum_v7_end ; if (N==0) goto end
checksum_v7_loop
LDR r3,[r0],#4 ; r3 = *(data++)
SUBS r1,r1,#1
; N-- and set flags
ADD r2,r3,r2
; sum += r3
BNE checksum_v7_loop ; if (N!=0) goto loop
checksum_v7_end
MOV r0,r2
; r0 = sum
MOV pc,r14
; return r0请注意,在函数入口处,编译器检查N是否为非零值。通常情况下,这个检查是不必要的,因为你知道数组不会为空。在这种情况下,使用do-while循环比for循环具有更好的性能和代码密度。
示例5.3展示了如何使用do-while循环来消除for循环中对N为零进行测试的情况。
int checksum_v8(int *data, unsigned int N)
{
int sum=0;
do
{
sum += *(data++);
} while (--N!=0);
return sum;
}The compiler output is now
checksum_v8
MOV r2,#0
; sum = 0
checksum_v8_loop
LDR r3,[r0],#4 ; r3 = *(data++)
SUBS r1,r1,#1
; N-- and set flags
ADD r2,r3,r2
; sum += r3
BNE checksum_v8_loop ; if (N!=0) goto loop
MOV r0,r2
; r0 = sum
MOV pc,r14
; return r0请将checksum_v8与checksum_v7的输出进行比较,以了解两个循环节约了两个周期的情况。
5.3.3 Loop Unrolling
//循环展开
在5.3.1节中我们看到,每个循环迭代除了循环体本身外还需要两条指令:一个减法指令来递减循环计数器,一个条件分支指令。我们称这些指令为循环开销(loop overhead)。在ARM7或ARM9处理器上,减法指令需要一个周期,分支指令需要三个周期,因此每次循环的开销为四个周期。
通过展开循环,可以节省一些周期,即重复执行循环体多次,并相应地减少循环迭代的次数。例如,让我们将我们的数据包校验和示例展开四次。
示例5.4展示了将数据包校验和循环展开四次的代码。我们假设数据包中的字(words)数量N是四的倍数。
int checksum_v9(int *data, unsigned int N)
{
int sum=0;
do
{
sum += *(data++);
sum += *(data++);
sum += *(data++);
sum += *(data++);
N -= 4;
} while ( N!=0);
return sum;
}This compiles to
checksum_v9
MOV r2,#0 ; sum = 0
checksum_v9_loop
LDR r3,[r0],#4 ; r3 = *(data++)
SUBS r1,r1,#4
; N -= 4 & set flags
ADD r2,r3,r2
; sum += r3
LDR r3,[r0],#4 ; r3 = *(data++)
ADD r2,r3,r2
; sum += r3
LDR r3,[r0],#4 ; r3 = *(data++)
ADD r2,r3,r2
; sum += r3
LDR r3,[r0],#4 ; r3 = *(data++)
ADD r2,r3,r2
; sum += r3
BNE checksum_v9_loop ; if (N!=0) goto loop
MOV r0,r2
; r0 = sum
MOV pc,r14
; return r0我们将循环的开销从4N个周期减少到(4N)/4=N个周期。在ARM7TDMI上,这将使循环每次累加的周期数从8个减少到20/4=5个,几乎使速度翻倍!对于具有更快加载指令的ARM9TDMI来说,效果甚至更好。
//这个当前编译器是不是已经优化了?
在展开循环时,你需要回答两个问题:
1. 我应该展开循环多少次?
2. 如果循环迭代的次数不是展开数量的倍数会怎样?例如,在checksum_v9中,如果N不是4的倍数会怎么办?
对于第一个问题,只有关乎应用程序整体性能的循环才值得展开。否则,展开只会增加代码大小而带来很少的性能提升。展开甚至可能通过将更重要的代码从缓存中驱逐出去而降低性能。
假设循环很重要,例如占整个应用程序的30%。假设你将循环展开直到达到0.5 KB的代码大小(128条指令)。那么,与大约128个周期的循环体相比,循环的开销最多为4个周期。循环开销成本为3/128,大约为3%。回想一下,假如循环占整个应用程序的30%,因此整体上循环开销只有1%。进一步展开代码几乎没有额外的性能收益,但对缓存内容有显著影响。当增益小于1%时,通常不值得继续展开。
对于第二个问题,请尽量安排数组大小是展开数量的倍数。如果不可能,那么你必须添加额外的代码来处理剩余的情况。这会稍微增加代码大小,但保持性能高效。
示例5.5
这个示例使用展开了四次的循环来处理任意大小的数据包的校验和。
int checksum_v10(int *data, unsigned int N)
{
unsigned int i;
int sum=0;
for (i=N/4; i!=0; i--)
{
sum += *(data++);
sum += *(data++);
sum += *(data++);
sum += *(data++);
}
for (i=N&3; i!=0; i--)
{
sum += *(data++);
}
return sum;
}第二个for循环处理当N不是4的倍数时的剩余情况。注意,N/4和N&3都可能为零,所以我们不能使用do-while循环。
有效地编写循环总结如下:
- 使用向零计数的循环。这样编译器就不需要分配一个寄存器来存储终止值,并且与零比较是免费的。
- 默认使用无符号的循环计数器和继续条件i!=0,而不是i>0。这将确保循环开销只有两个指令。
- 当你知道循环至少会执行一次时,使用do-while循环而不是for循环。这样可以避免编译器检查循环计数是否为零。
- 为了减少循环开销,展开重要的循环。但不要过度展开。如果循环开销在总体上占比很小,那么展开会增加代码大小,并对缓存性能造成影响。
- 尽量安排数组中的元素数量是四或八的倍数。这样,你可以轻松地将循环展开两倍、四倍或八倍,而不用担心剩余的数组元素问题。
5.4 Register Allocation
编译器会尝试为C函数中使用的每个局部变量分配一个处理器寄存器。如果变量的使用不重叠,编译器将尝试为不同的局部变量使用相同的寄存器。当局部变量的数量超过可用寄存器时,编译器将多余的变量存储在处理器栈上。这些变量被称为溢出变量或交换出的变量,因为它们被写入内存(类似于虚拟内存被交换到磁盘上)。与分配给寄存器的变量相比,访问溢出变量的速度较慢。
为了高效实现函数,你需要:
- 最小化溢出变量的数量
- 确保最重要和频繁访问的变量存储在寄存器中
首先,让我们看一下ARM C编译器在分配变量时可用的处理器寄存器数量。表5.3显示了按照ARM-Thumb过程调用标准(ATPCS)进行编码时的标准寄存器名称和用法。

C compiler register usage:
a1~a4: 参数寄存器。这些寄存器在函数调用时保存前四个函数参数,在函数返回时保存返回值。函数可能会破坏这些寄存器,并在函数内部将它们用作通用的临时寄存器。
v1~v5: 通用变量寄存器。函数必须保留这些寄存器的被调用者值。
v6 sb: 通用变量寄存器。函数必须保留该寄存器的被调用者值,除非编译时为读写位置无关性(RWPI)。然后r9保存静态基址。这是读写数据的地址。
v7 sl: 通用变量寄存器。函数必须保留该寄存器的被调用者值,除非在进行栈限制检查编译时。此时,r10保存栈限制地址。
v8 fp: 通用变量寄存器。函数必须保留该寄存器的被调用者值,除非使用帧指针进行编译。只有旧版本的armcc使用帧指针。
ip: 一个通用的临时寄存器,函数可以覆盖其中的值。它对于函数过程中的需求或其他函数调用要求作为临时寄存器来使用是很有用的。
sp: 栈指针,指向完整的降序堆栈。
lr: 链接寄存器。在函数调用中,它保存返回地址。
pc: 程序计数器。
假设编译器没有使用软件栈检查或帧指针,ARM C编译器可以使用r0到r12和r14寄存器来保存变量。如果使用这些寄存器,它必须在栈上保存r4到r11和r14的调用者值。
理论上,C编译器可以分配14个变量到寄存器而不产生溢出。但实际上,一些编译器会将某些寄存器(如r12)固定为中间临时工作寄存器,并不将变量分配给该寄存器。此外,复杂的表达式需要中间工作寄存器进行求值。因此,为了确保良好的寄存器分配,应尽量限制函数内部循环使用的局部变量数量不超过12个。
如果编译器确实需要交换变量,则它会根据使用频率选择要交换的变量。在循环内使用的变量会被计算多次。通过在最内层循环中使用这些变量,你可以告诉编译器哪些变量很重要。
在C中,register关键字提示编译器应该将给定的变量分配给一个寄存器。然而,不同的编译器对待这个关键字的方式不同,不同的体系结构有不同数量的可用寄存器(例如Thumb和ARM)。因此,建议避免使用register,并依赖于编译器的正常寄存器分配例程。
总结高效的寄存器分配方法:
- 尽量限制函数内部循环中的局部变量数量不超过12个。编译器应该能够将这些变量分配给ARM寄存器。
- 通过在最内层循环中使用这些变量,可以告诉编译器哪些变量很重要。
5.5 Function Calls

ARM过程调用标准(APCS)定义了在ARM寄存器中如何传递函数参数和返回值。更近期的ARM-Thumb过程调用标准(ATPCS)覆盖了ARM和Thumb之间的交互工作。前四个整数参数通过前四个ARM寄存器(r0、r1、r2和r3)传递。后续的整数参数按照图5.1中所示的方式,从上到下依次放置在降序堆栈中。函数返回的整数值存放在r0中。此描述仅涵盖整数或指针参数。例如long long或double等双字参数会以一对连续的参数寄存器传递,并在r0、r1中返回。编译器可以根据命令行编译选项将结构体参数传递给寄存器或通过引用传递。关于过程调用标准的首要注意事项是四个寄存器规则。调用具有四个或更少参数的函数比调用具有五个或更多参数的函数更高效。对于具有四个或更少参数的函数,编译器可以将所有参数传递到寄存器中。对于具有更多参数的函数,调用方和被调用方都必须对某些参数访问堆栈。请注意,对于C++而言,对象方法的第一个参数是this指针。此参数是隐含的,与显式参数不同。如果您的C函数需要超过四个参数,或者C++方法需要超过三个显式参数,那么使用结构体几乎总是更高效的方法。将相关参数组合成结构体,并传递结构体指针而不是多个参数。哪些参数是相关的将取决于您软件的结构。
下面的示例说明了使用结构体指针的好处。首先,我们展示了一个典型的例程,将来自数组数据的N个字节插入队列中。我们使用循环缓冲区实现队列,起始地址为Q_start(包含),结束地址为Q_end(不包含)。
char *queue_bytes_v1(
char *Q_start, /* Queue buffer start address */
char *Q_end,
/* Queue buffer end address */
char *Q_ptr,
/* Current queue pointer position */
char *data,
/* Data to insert into the queue */
unsigned int N) /* Number of bytes to insert */
{
do
{
*(Q_ptr++) = *(data++);
if (Q_ptr == Q_end)
{
Q_ptr = Q_start;
}
} while (--N);
return Q_ptr;
}This compiles to
queue_bytes_v1
STR r14,[r13,#-4]! ; save lr on the stack
LDR r12,[r13,#4] ; r12 = N
queue_v1_loop
LDRB r14,[r3],#1 ; r14 = *(data++)
STRB r14,[r2],#1 ; *(Q_ptr++) = r14
CMP r2,r1
; if (Q_ptr == Q_end)
MOVEQ r2,r0
; {Q_ptr = Q_start;}
SUBS r12,r12,#1 ; --N and set flags
BNE queue_v1_loop ; if (N!=0) goto loop
MOV r0,r2
; r0 = Q_ptr
LDR pc,[r13],#4 ; return r0与使用三个函数参数的更结构化方法进行比较。示例5.6中的以下代码创建了一个Queue结构,并将其传递给函数,以减少函数参数的数量。
typedef struct {
char *Q_start; /* Queue buffer start address */
char *Q_end;
/* Queue buffer end address */
char *Q_ptr;
/* Current queue pointer position */
} Queue;
void queue_bytes_v2(Queue *queue, char *data, unsigned int N)
{
char *Q_ptr = queue->Q_ptr;
char *Q_end = queue->Q_end;
do
{
*(Q_ptr++) = *(data++);
if (Q_ptr == Q_end)
{
Q_ptr = queue->Q_start;
}
} while (--N);
queue->Q_ptr = Q_ptr;
}This compiles to
queue_bytes_v2
STR r14,[r13,#-4]! ; save lr on the stack
LDR r3,[r0,#8] ; r3 = queue->Q_ptr
LDR r14,[r0,#4] ; r14 = queue->Q_end
queue_v2_loop
LDRB r12,[r1],#1 ; r12 = *(data++)
STRB r12,[r3],#1 ; *(Q_ptr++) = r12
CMP r3,r14
; if (Q_ptr == Q_end)
LDREQ r3,[r0,#0] ; Q_ptr = queue->Q_start
SUBS r2,r2,#1 ; --N and set flags
BNE queue_v2_loop ; if (N!=0) goto loop
STR r3,[r0,#8] ; queue->Q_ptr = r3
LDR pc,[r13],#4 ; returnqueue_bytes_v2比queue_bytes_v1多了一条指令,但实际上总体上更高效。第二个版本只有三个函数参数,而不是五个。每次调用函数只需要三个寄存器的设置。与第一个版本相比,第一个版本需要四个寄存器的设置、一个栈的压入和一个栈的弹出。函数调用开销净节省了两条指令。在被调用函数中也可能有进一步的节省,因为它只需要将一个寄存器分配给Queue结构体指针,而不是非结构化情况下的三个寄存器。
如果您的函数非常小且破坏的寄存器很少(使用的本地变量很少),还有其他减少函数调用开销的方法。将C函数放在与调用它的函数相同的C文件中。这样,C编译器就知道对被调用函数生成的代码,并且可以在调用者函数中进行优化:
- 调用者函数不需要保留它可以看到被调用函数不会破坏的寄存器。因此,调用者函数不需要保存所有可能被ATPCS破坏的寄存器。
- 如果被调用函数非常小,编译器可以将代码内联到调用者函数中。这完全消除了函数调用的开销。
示例5.7中的函数uint_to_hex将一个32位无符号整数转换为一个包含八个十六进制数的数组。它使用一个辅助函数nybble_to_hex,该函数将范围在0到15之间的数字d转换为一个十六进制数。
unsigned int nybble_to_hex(unsigned int d)
{
if (d<10)
{
return d + ’0’;
}
return d - 10 + ’A’;
}
void uint_to_hex(char *out, unsigned int in)
{
unsigned int i;
for (i=8; i!=0; i--)
{
in = (in << 4) | (in >> 28); /* rotate in left by 4 bits */
*(out++) = (char)nybble_to_hex(in & 15);
}
}当我们编译这段代码时,我们可以看到uint_to_hex根本没有调用nybble_to_hex!在下面的编译代码中,编译器已经将uint_to_hex代码内联展开了。这比生成函数调用更高效。
uint_to_hex
MOV r3,#8
;i=8
uint_to_hex_loop
MOV r1,r1,ROR #28 ; in = (in << 4)|(in >> 28)
AND r2,r1,#0xf ; r2 = in & 15
CMP r2,#0xa
; if (r2>=10)
ADDCS r2,r2,#0x37 ; r2 +=’A’-10
ADDCC r2,r2,#0x30 ; else r2 +=’0’
STRB r2,[r0],#1 ; *(out++) = r2
SUBS r3,r3,#1
; i-- and set flags
BNE uint_to_hex_loop ; if (i!=0) goto loop
MOV pc,r14
; return编译器只会内联展开小函数。您可以使用__inline关键字让编译器内联展开函数,尽管这个关键字只是一个暗示,编译器也可能会忽略它(有关内联函数的更多信息,请参见第5.12节)。内联展开大函数可能会导致代码大小大幅增加,而性能改善不明显。
总结:
- 尽量将函数限制在四个参数内。这样可以使它们更高效地调用。使用结构体来组织相关的参数,而不是传递多个参数。
- 在调用它们的函数之前,将小函数定义在同一个源文件中。然后编译器可以优化函数调用或者内联展开小函数。
- 可以使用__inline关键字内联展开关键函数。
5.6 Pointer Aliasing
//指针别名
当两个指针指向相同的内存地址时,它们被称为别名。如果您通过一个指针对其进行写操作,将会影响通过另一个指针读取的值。在函数中,编译器通常无法确定哪些指针可以别名,哪些不能。编译器必须非常保守,并假设对一个指针的任何写操作都可能影响到从任何其他指针读取的值。这可能会显著降低代码的效率。
让我们从一个非常简单的例子开始。下面的函数按照给定的步长递增两个计时器的值:
void timers_v1(int *timer1, int *timer2, int *step)
{
*timer1 += *step;
*timer2 += *step;
}This compiles to
timers_v1
LDR r3,[r0,#0] ; r3 = *timer1
LDR r12,[r2,#0] ; r12 = *step
ADD r3,r3,r12 ; r3 += r12
STR r3,[r0,#0] ; *timer1 = r3
LDR r0,[r1,#0] ; r0 = *timer2
LDR r2,[r2,#0] ; r2 = *step
ADD r0,r0,r2
; r0 += r2
STR r0,[r1,#0] ; *timer2 = t0
MOV pc,r14
; return请注意,编译器两次加载了step。通常情况下,一个称为共同子表达式消除的编译器优化会生效,这样*step只会被计算一次,并且第二次出现时会重用该值。然而,在这里编译器无法使用这种优化。指针timer1和step可能会别名。换句话说,编译器无法确定对timer1的写操作不会影响到对step的读取。在这种情况下,*step的第二个值与第一个值不同,并且具有*timer1的值。这会迫使编译器插入额外的加载指令。
如果您使用结构体访问而不是直接指针访问,同样的问题也会发生。以下代码也会编译得低效:
typedef struct {int step;} State;
typedef struct {int timer1, timer2;} Timers;
void timers_v2(State *state, Timers *timers)
{
timers->timer1 += state->step;
timers->timer2 += state->step;
}当state->step和timers->timer1位于相同的内存地址时,编译器会对state->step进行两次评估。修复方法很简单:创建一个新的局部变量来保存state->step的值,这样编译器只需执行一次加载。
示例5.8:
在timers_v3的代码中,我们使用一个名为step的局部变量来保存state->step的值。现在编译器不需要担心state可能与timers别名的问题了。
void timers_v3(State *state, Timers *timers)
{
int step = state->step;
timers->timer1 += step;
timers->timer2 += step;
}还要注意其他一些不太明显的情况,可能会发生别名问题。当调用另一个函数时,该函数可能会改变内存状态,从而改变任何涉及内存读取的表达式的值。编译器将重新评估表达式。例如,假设您读取state->step,调用一个函数,然后再次读取state->step。编译器必须假定函数可能会更改内存中state->step的值。因此,它将执行两次读取,而不是重复使用它读取state->step的第一个值。
另一个陷阱是取本地变量的地址。一旦这样做,该变量就会被指针引用,因此可以与其他指针发生别名问题。编译器可能会保持从堆栈中读取变量,以防别名出现。考虑以下示例,它读取并计算数据包的校验和:
int checksum_next_packet(void)
{
int *data;
int N, sum=0;
data = get_next_packet(&N);
do
{
sum += *(data++);
} while (--N);
return sum;
}这里get_next_packet是一个函数,返回下一个数据包的地址和大小。前面的代码编译为:
checksum_next_packet
STMFD r13!,{r4,r14} ; save r4, lr on the stack
SUB r13,r13,#8
; create two stacked variables
ADD r0,r13,#4
; r0 = &N, N stacked
MOV r4,#0
; sum = 0
BL get_next_packet ; r0 = data
checksum_loop
LDR r1,[r0],#4
; r1 = *(data++)
ADD r4,r1,r4
; sum += r1
LDR r1,[r13,#4] ; r1 = N (read from stack)
SUBS r1,r1,#1
; r1-- & set flags
STR r1,[r13,#4]
; N = r1 (write to stack)
BNE checksum_loop ; if (N!=0) goto loop
MOV r0,r4
; r0 = sum
ADD r13,r13,#8
; delete stacked variables
LDMFD r13!,{r4,pc} ; return r0请注意,编译器在每次N--时从堆栈中读取并写入N的值。一旦您取出N的地址并将其传递给get_next_packet,编译器就需要担心别名问题,因为指针data和&N可能会发生别名问题。为了避免这种情况,不要取本地变量的地址。如果必须这样做,则在使用之前将值复制到另一个本地变量中。
也许您想知道为什么编译器为两个堆栈变量预留空间,而实际上只使用了一个。这是为了保持堆栈按8字节对齐,这是ARMv5TE中可用的LDRD指令所需的。上面的示例实际上并没有使用LDRD指令,但编译器不知道get_next_packet是否会使用该指令。
避免指针别名问题的总结:
- 不要依赖编译器消除涉及内存访问的公共子表达式。相反,创建新的本地变量来保存表达式。这样可以确保表达式只被评估一次。
- 避免获取本地变量的地址。之后从该地址访问该变量可能会导致效率低下。
5.7 Structure Arrangement
您布置经常使用的结构体的方式可能对其性能和代码密度产生重大影响。在ARM上有两个与结构体相关的问题:结构体条目的对齐和结构体的整体大小。
对于包括ARMv5TE在内的架构,加载和存储指令只能保证加载和存储与访问宽度对齐的地址处的值。表5.4总结了这些限制。

基于这个原因,ARM编译器会自动将结构的起始地址对齐为结构中使用的最大访问宽度(通常为四个或八个字节)的倍数,并通过插入填充来对齐结构中的条目到其访问宽度。
例如,考虑以下结构:
struct {
char a;
int b;
char c;
short d;
}对于小端内存系统,编译器会布置结构并添加填充,以确保下一个对象对齐到该对象的大小:

为了改善内存使用情况,您应该重新排列元素。
struct {
char a;
char c;
short d;
int b;
}这将结构的大小从12字节减小到8字节,具有以下新的布局:

因此,将结构元素按照相同的大小进行分组是一个好主意,这样结构布局就不会包含不必要的填充。armcc编译器确实包含了一个名为`__packed`的关键字,可以移除所有的填充。例如,下面的结构:
__packed struct {
char a;
int b;
char c;
short d;
}will be laid out in memory as

然而,紧凑的结构在访问时会变得较慢且效率低下。编译器通过使用多个对齐的访问和数据操作来模拟非对齐的加载和存储操作,并将结果合并。只有在空间远比速度重要且无法通过重新排列来减少填充时,才使用`__packed`关键字。同时,在移植代码时,如果代码假设特定的结构布局存在于内存中,则也可以使用该关键字。
结构在内存中的确切布局可能取决于您使用的编译器供应商和编译器版本。在API(应用程序编程接口)定义中,插入任何无法消除的填充到结构中通常是一个好主意。这样可以避免结构布局的歧义。如果坚持使用明确的结构,更容易在不同的编译器版本和供应商之间链接代码。
另一个不确定性点是enum枚举类型。不同的编译器根据枚举的范围使用不同大小的枚举类型。例如,考虑以下类型:
typedef enum {
FALSE,
TRUE
} Bool;在ADS1.1中,armcc编译器将Bool类型作为一个字节类型处理,因为它只使用值0和1。在结构中,Bool类型只占用8位空间。然而,在gcc中,Bool类型将被视为一个字,并在结构中占用32位空间。为避免歧义,在API中尽量避免在结构中使用枚举类型。
另一个考虑因素是结构的大小和结构内元素的偏移量。当使用Thumb指令集进行编译时,这个问题最为严重。Thumb指令只有16位宽度,因此只允许从结构基地址偏移较小的元素。表5.5显示了在Thumb中可用的加载和存储基寄存器的偏移量。

因此,如果8位元素出现在结构的前32字节内,编译器只能使用单条指令访问这个8位元素。类似地,只有在前64字节内才能使用单条指令访问16位值,并且只有在前128字节内才能使用单条指令访问32位值。一旦超过这些限制,结构访问效率就会降低。
为了实现最大效率的紧凑结构,可以遵循以下规则:
- 将所有的8位元素放在结构的开头。
- 接下来放置所有的16位元素,然后是32位和64位元素。
- 将所有的数组和较大的元素放在结构的末尾。
- 如果结构过大,无法使用单条指令访问所有元素,则将元素分组到子结构中。编译器可以维护对各个子结构的指针。
总结 高效的结构排列方法如下:
- 按照元素大小递增的顺序布置结构。从最小的元素开始,以最大的元素结束。
- 避免使用非常大的结构。而是使用一系列较小的结构层次。
- 为了可移植性,在API结构中手动添加填充(隐含地出现) ,以使结构的布局不依赖于编译器。
- 注意在API结构中使用枚举类型。枚举类型的大小取决于编译器。
5.8 Bit-fields
位字段可能是ANSI C规范中最不标准化的部分。编译器可以选择如何在位字段容器内分配位。单单因为这个原因,避免在联合体或API结构定义中使用位字段。不同的编译器可以将相同的位字段分配给容器中的不同位位置。
出于效率考虑,避免使用位字段也是一个好主意。位字段是结构元素,通常使用结构指针进行访问;因此,它们受到第5.6节中描述的指针别名问题的影响。每次位字段访问实际上都是一次内存访问。可能的指针别名经常迫使编译器多次重新加载位字段。
下面的例子 dostages_v1 就说明了这个问题。它还显示了编译器在位字段测试方面不倾向于进行优化。
void dostageA(void);
void dostageB(void);
void dostageC(void);
typedef struct {
unsigned int stageA : 1;
unsigned int stageB : 1;
unsigned int stageC : 1;
} Stages_v1;
void dostages_v1(Stages_v1 *stages)
{
if (stages->stageA)
{
dostageA();
}
if (stages->stageB)
{
dostageB();
}
if (stages->stageC)
{
dostageC();
}
}在这里,我们使用三个位字段标志来启用三个可能的处理阶段。这个示例编译为:
dostages_v1
STMFD r13!,{r4,r14} ; stack r4, lr
MOV r4,r0
; move stages to r4
LDR r0,[r0,#0] ; r0 = stages bitfield
TST r0,#1
; if (stages->stageA)
BLNE dostageA
; {dostageA();}
LDR r0,[r4,#0] ; r0 = stages bitfield
MOV r0,r0,LSL #30 ; shift bit 1 to bit 31
CMP r0,#0
; if (bit31)
BLLT dostageB
; {dostageB();}
LDR r0,[r4,#0] ; r0 = stages bitfield
MOV r0,r0,LSL #29 ; shift bit 2 to bit 31
CMP r0,#0
; if (!bit31)
LDMLTFD r13!,{r4,r14} ; return
BLT dostageC
; dostageC();
LDMFD r13!,{r4,pc} ; return请注意,编译器三次访问包含位字段的内存位置。由于位字段存储在内存中,dostage函数可以更改其值。此外,编译器使用两个指令来测试位字段的位1和位2,而不是单个指令。
通过使用整数而不是位字段,您可以生成更高效的代码。使用枚举或#define掩码将整数类型划分为不同的字段。
以下代码实现了使用逻辑操作而不是位字段的dostages函数的示例:
typedef unsigned long Stages_v2;
#define STAGEA (1ul << 0)
#define STAGEB (1ul << 1)
#define STAGEC (1ul << 2)
void dostages_v2(Stages_v2 *stages_v2)
{
Stages_v2 stages = *stages_v2;
if (stages & STAGEA)
{
dostageA();
}
if (stages & STAGEB)
{
dostageB();
}
if (stages & STAGEC)
{
dostageC();
}
}现在,一个单独的unsigned long类型包含了所有的位字段,我们可以将它们的值保存在一个单独的局部变量stages中,这样就消除了第5.6节中讨论的内存别名问题。换句话说,编译器必须假设dostageX(其中X是A、B或C)函数可能会改变*stages_v2的值。
编译器生成以下代码,相比使用ANSI位字段的先前版本,节省了33%的空间:
dostages_v2
STMFD r13!,{r4,r14} ; stack r4, lr
LDR r4,[r0,#0] ; stages = *stages_v2
TST r4,#1
; if (stage & STAGEA)
BLNE dostageA ; {dostageA();}
TST r4,#2
; if (stage & STAGEB)
BLNE dostageB ; {dostageB();}
TST r4,#4
; if (!(stage & STAGEC))
LDMNEFD r13!,{r4,r14} ; return;
BNE dostageC ; dostageC();
LDMFD r13!,{r4,pc} ; return您还可以使用掩码来设置、清除或切换位字段,就像对它们进行测试一样简单。以下代码展示了如何使用STAGE掩码来设置、清除或切换位的示例:
stages |= STAGEA;
/* enable stage A */
stages &= ∼STAGEB; /* disable stage B */
stages ∧= STAGEC;
/* toggle stage C */这些位设置、清除和切换操作每个只需要一条ARM指令,分别使用ORR、BIC和EOR指令。另一个优点是现在您可以使用一条指令同时操作多个位字段。例如:
stages |= (STAGEA | STAGEB);
/* enable stages A and B */
stages &= ∼(STAGEA | STAGEC); /* disable stages A and C */总结位字段的使用方法:
- 避免使用位字段,而是使用#define或enum来定义掩码值。
- 使用整数逻辑的与、或、异或操作和掩码值来测试、切换和设置位字段。这些操作在编译时效率高,并且可以同时测试、切换或设置多个字段。
5.9 Unaligned Data and Endianness
未对齐的数据和字节序是可能使内存访问和可移植性复杂化的两个问题。数组指针是否对齐?ARM配置为大端或小端内存系统?
ARM的加载和存储指令假设地址是要加载或存储的类型的倍数。如果加载或存储到的地址与其类型不对齐,则行为取决于特定的实现。核心可能会生成数据中止或加载旋转值。对于良好编写的可移植代码,应避免非对齐访问。
C编译器默认假设指针是对齐的,除非另有说明。如果指针未对齐,程序可能会产生意外结果。当将代码从允许非对齐访问的处理器移植到ARM时,这有时是一个问题。对于armcc编译器,__packed指令告诉编译器数据项可以位于任何字节对齐位置。这对于移植代码很有用,但使用__packed会影响性能。
为了说明这一点,我们看下面这个简单的例程readint。它返回data指针所指向的地址处的整数。我们使用__packed告诉编译器整数可能未对齐。
int readint(__packed int *data)
{
return *data;
}This compiles to
readint
BIC r3,r0,#3
; r3 = data & 0xFFFFFFFC
AND r0,r0,#3
; r0 = data & 0x00000003
MOV r0,r0,LSL #3 ; r0 = bit offset of data word
LDMIA r3,{r3,r12} ; r3, r12 = 8 bytes read from r3
MOV r3,r3,LSR r0 ; These three instructions
RSB r0,r0,#0x20 ; shift the 64 bit value r12.r3
ORR r0,r3,r12,LSL r0 ; right by r0 bits
MOV pc,r14
; return r0注意到这段代码非常庞大和复杂。编译器使用两次对齐访问和数据处理操作来模拟非对齐访问,这非常耗时,这也说明了为什么应该避免使用_packed。相反,可以使用char *类型的指针来指向可能以任何对齐方式出现的数据。稍后我们将介绍从char *中更高效地读取32位字的方法。
当读取用于在计算机之间传输信息的数据包或文件时,很可能会遇到对齐问题。网络数据包和压缩图像文件是很好的例子。这些文件中的两个或四个字节的整数可能出现在任意偏移量处。为了尽可能地压缩数据,牺牲了对齐。
字节序(或字节顺序)在读取数据包或压缩文件时也是一个重要问题。ARM核心可以配置为使用小端序(最低地址存放最不重要的字节)或大端序(最低地址存放最重要的字节)。小端序通常是默认设置。


ARM的字节序通常在上电时设置,并且在之后保持固定。表5.6和5.7说明了ARM的8位、16位和32位加载和存储指令在不同的字节序配置下的工作方式。我们假设字节地址A对齐到内存传输的大小。表格显示了指令加载或存储的字节地址如何映射到内存中的32位寄存器。
如果速度不是关键,处理字节序和对齐问题的最佳方式是使用像Example 5.10中的readint_little和readint_big这样的函数,它们从可能未对齐的内存地址中读取一个四字节整数。地址对齐只在运行时才能确定,而不是在编译时就已知。如果你加载的文件包含大端序数据,比如JPEG图像,那么使用readint_big函数。对于包含小端序数据的字节流,使用readint_little函数。无论ARM配置的内存字节序如何,这两个函数都能正确工作。
Example 5.10中的这些函数从data指向的字节流中读取一个32位整数。这些字节流分别包含小端序或大端序数据。这些函数独立于ARM内存系统的字节序,因为它们仅使用字节访问。
int readint_little(char *data)
{
int a0,a1,a2,a3;
a0 = *(data++);
a1 = *(data++);
a2 = *(data++);
a3 = *(data++);
return a0 | (a1 << 8) | (a2 << 16) | (a3 << 24);
}
int readint_big(char *data)
{
int a0,a1,a2,a3;
a0 = *(data++);
a1 = *(data++);
a2 = *(data++);
a3 = *(data++);
return (((((a0 << 8) | a1) << 8) | a2) << 8) | a3;
}如果速度至关重要,最快的方法是编写关键例程的多个变体。对于每种可能的对齐和ARM字节序配置,调用一个针对该情况进行优化的单独例程。
Example 5.11中的read_samples例程接受一个包含N个16位音频样本的数组,位于地址in处。音频样本是小端序(例如来自.wav文件),可以在任意字节对齐位置上。该例程将样本复制到由out指向的对齐的short类型值数组中。样本将按照配置的ARM内存字节序存储。该例程以高效的方式处理所有情况,无论输入对齐方式如何,以及ARM字节序配置如何。
void read_samples(short *out, char *in, unsigned int N)
{
unsigned short *data; /* aligned input pointer */
unsigned int sample, next;
switch ((unsigned int)in & 1)
{
case 0: /* the input pointer is aligned */
data = (unsigned short *)in;
do
{
sample = *(data++);
#ifdef __BIG_ENDIAN
sample = (sample >> 8) | (sample << 8);
#endif
*(out++) = (short)sample;
} while (--N);
break;
case 1: /* the input pointer is not aligned */
data = (unsigned short *)(in-1);
sample = *(data++);
#ifdef __BIG_ENDIAN
sample = sample & 0xFF; /* get first byte of sample */
#else
sample = sample >> 8; /* get first byte of sample */
#endif
do
{
next = *(data++);
/* complete one sample and start the next */
#ifdef __BIG_ENDIAN
*out++ = (short)((next & 0xFF00) | sample);
sample = next & 0xFF;
#else
*out++ = (short)((next << 8) | sample);
sample = next >> 8;
#endif
} while (--N);
break;
}
}该例程通过为每个字节序和对齐方式编写不同的代码来工作。字节序使用编译时的__BIG_ENDIAN编译器标志处理。对齐必须在运行时使用switch语句进行处理。
你可以通过使用32位读写而不是16位读写使例程更加高效,这样可以在switch语句中有四个元素,分别对应可能的地址对齐模4的情况。
总结:字节序和对齐方式
- 尽量避免使用未对齐的数据。
- 对于可以处于任意字节对齐位置的数据,使用char*类型。通过读取字节并与逻辑操作相结合来访问数据。这样代码就不会依赖于对齐或ARM字节序的配置。
- 对于快速访问未对齐的结构,根据指针对齐和处理器字节序编写不同的变体。
5.10 Division
ARM处理器在硬件中没有除法指令。相反,编译器通过调用C库中的软件例程来实现除法运算。你可以根据特定的分子和分母值范围来定制许多不同类型的除法例程。我们将在第7章中详细讨论汇编除法例程。C库中提供的标准整数除法例程的执行时间根据实现、早期终止和输入操作数的范围而有所不同,通常需要20到100个周期。
除法和取模(/和%)是非常慢的操作,应尽量避免使用它们。然而,对于常数除法和反复除以相同分母的情况,可以高效地进行处理。本节将介绍如何通过乘法替代某些除法,并尽量减少除法调用的次数。
循环缓冲区是程序员经常使用除法的一个领域,但完全可以避免使用这些除法。假设你有一个大小为buffer_size字节的循环缓冲区,并且有一个由缓冲区偏移指示的位置。要通过increment字节来推进偏移量,你可以写成:
offset = (offset + increment) % buffer_size;
但实际上,更高效的写法是:
offset += increment;
if (offset>=buffer_size)
{
offset -= buffer_size;
}第一个版本可能需要50个周期;而第二个版本将只需3个周期,因为它不涉及除法运算。我们假设increment < buffer_size;在实际应用中你总是可以满足这个条件。
如果无法避免使用除法,那么尽量确保分子和分母是无符号整数。有符号除法例程速度较慢,因为它们会取分子和分母的绝对值,然后调用无符号除法例程。之后再修复结果的符号。
许多C库的除法例程返回除法的商和余数。换句话说,每次除法操作都可以获得免费的余数操作,反之亦然。例如,要找到位于屏幕缓冲区偏移offset字节处的位置(x, y),很容易写成:
typedef struct {
int x;
int y;
} point;
point getxy_v1(unsigned int offset, unsigned int bytes_per_line)
{
point p;
p.y = offset / bytes_per_line;
p.x = offset - p.y * bytes_per_line;
return p;
}看起来我们通过使用减法和乘法来计算p.x,避免了一次除法操作,但实际上,使用模运算或余数运算符往往更高效。
示例5.12:
在getxy_v2中,商和余数的操作只需要调用一次除法例程:
point getxy_v2(unsigned int offset, unsigned int bytes_per_line)
{
point p;
p.x = offset % bytes_per_line;
p.y = offset / bytes_per_line;
return p;
}在这里只有一次除法调用,正如您可以在下面的编译器输出中看到的那样。实际上,这个版本比getxy_v1短了四条指令。请注意,对于所有的编译器和C库来说,情况可能并非总是如此。
getxy_v2
STMFD r13!,{r4, r14} ; stack r4, lr
MOV r4,r0
; move p to r4
MOV r0,r2
; r0 = bytes_per_line
BL __rt_udiv ; (r0,r1) = (r1/r0, r1%r0)
STR r0,[r4,#4] ; p.y = offset / bytes_per_line
STR r1,[r4,#0] ; p.x = offset % bytes_per_line
LDMFD r13!,{r4,pc} ; return5.10.1 Repeated Unsigned Division with Remainder
//重复的无符号除法和余数运算
在代码中经常会出现相同的分母多次重复的情况。在前面的例子中,bytes_per_line可能在整个程序中保持不变。如果我们从三维笛卡尔坐标投影到二维坐标,那么我们会使用两次分母:
(x, y, z) → (x/z, y/z)
在这些情况下,更有效的做法是以某种方式缓存1/z的值,并使用乘法1/z代替除法。接下来的子节中,我们将展示如何做到这一点。此外,我们还希望坚持使用整数运算,避免使用浮点数(参见第5.11节)。
下面的描述相对较数学化,涵盖了将重复的除法转换为乘法的背后理论。如果您对这个理论不感兴趣,那么不要担心。您可以直接跳到接下来的示例5.13。
5.10.2 Converting Divides into Multiplies
//这个有意思了!像研究生<计算方法>的课程
为了区分精确的数学除法和整数除法,我们将使用以下符号表示:
■ n/d = n除以d的整数部分,向零取整(与C语言中的行为相同)
■ n%d = n除以d的余数,即n - d * (n / d)
■ n/d = nd^(-1) = n除以d的真实数学除法
在坚持使用整数运算的情况下,估计d^(-1)的一种明显方法是计算2^32/d。然后我们可以估计n/d的值
![]()
这种方法需要以64位精度执行乘以n的操作。这种方法存在一些问题:
■ 要计算2^32/d,编译器需要使用64位的long long类型进行算术运算,因为2^32不能适应unsigned int类型。我们必须将除法指定为(1ull << 32)/d。这种64位除法比我们最初想要执行的32位除法要慢得多!
■ 如果d恰好为1,那么2^32/d将不能适应unsigned int类型。
事实证明,稍微粗略的估计方法效果很好,并且解决了这两个问题。我们可以考虑使用(2^32-1)/d而不是2^32/d。
定义 s = 0xFFFFFFFFul / d; /* s = (2^32-1)/d */
我们可以使用单个unsigned int类型的除法来计算s。我们知道

接下来,计算一个对n/d的估计值q:
q = (unsigned int)( ((unsigned long long)n * s) >> 32);
从数学上讲,右移32位引入了一个误差e2:

因此,q = n/d或q = (n/d) - 1。我们可以通过计算余数r = n - qd来很容易地找到它的值,该余数必须在0 ≤ r < 2d范围内。以下代码纠正了结果:
r = n - q * d; /* 余数在范围0 <= r < 2 * d内 */
if (r >= d) /* 如果需要修正 */
{
r -= d; /* 将余数修正为0 <= r < d的范围内 */
q++; /* 修正商 */
}
/* 现在q = n / d且r = n % d */例子5.13
下面这个例程scale展示了如何在实践中将除法转换为乘法。它将一个具有N个元素的数组除以分母d。我们首先按上述方法计算s的值。然后,我们将每个除法替换为乘以s的乘法。64位乘法是便宜的,因为ARM具有UMULL指令,它可以将两个32位值相乘,得到一个64位结果。
void scale(
unsigned int *dest,
/* destination for the scale data */
unsigned int *src,
/* source unscaled data */
unsigned int d,
/* denominator to divide by */
unsigned int N) /* data length */
{
unsigned int s = 0xFFFFFFFFu / d;
do
{
unsigned int n, q, r;
n = *(src++);
q = (unsigned int)(((unsigned long long)n * s) >> 32);
r = n - q * d;
if (r >= d)
{
q++;
}
*(dest++) = q;
} while (--N);
}在这里,我们假设分子和分母是32位的无符号整数。当然,对于使用32位乘法的16位无符号整数,或者使用128位乘法的64位整数,该算法同样适用。你应该选择你的数据的最窄宽度。如果你的数据是16位的,那么将s = (2^16 - 1)/d设置为估计的q,使用标准整数C乘法进行估计。
5.10.3 Unsigned Division by a Constant
要除以一个常数c,你可以使用示例5.13的算法,预先计算s = (2^32 - 1)/c。然而,还有一种更高效的方法。ADS1.2编译器使用这种方法来合成对常数的除法。
这个想法是使用一个足够精确的d-1的近似值,以便通过近似值相乘得到n/d的精确值。我们使用以下数学结果:


对于这两个方程,右边的范围为0 ≤ x < 2N+k。对于32位无符号整数n,我们取N = 32,选择一个k,使得2k < d ≤ 2k+1,并设置s = (2N+k + 2k)/d。
如果ds ≥ 2N+k,那么n/d = (ns) << (N + k);否则,n/d = (ns + s) << (N + k)。作为额外的优化,如果d是2的幂次,我们可以用移位操作替代除法。
例子5.14
函数udiv_by_const测试了上述算法。在实际应用中,d将是一个固定的常数而不是一个变量。你可以预先计算s和k,并只包括与你特定的d值相关的计算。
unsigned int udiv_by_const(unsigned int n, unsigned int d)
{
unsigned int s,k,q;
/* We assume d!=0 */
/* first find k such that (1 << k) <= d < (1 << (k+1)) */
for (k=0; d/2>=(1u << k); k++);
if (d==1u << k)
{
/* we can implement the divide with a shift */
return n >> k;
}
/* d is in the range (1 << k) < d < (1 << (k+1)) */
s = (unsigned int)(((1ull << (32+k))+(1ull << k))/d);
if ((unsigned long long)s*d >= (1ull << (32+k)))
{
/* n/d = (n*s) >> (32+k) */
q = (unsigned int)(((unsigned long long)n*s) >> 32);
return q >> k;
}
/* n/d = (n*s+s) >> (32+k) */
q = (unsigned int)(((unsigned long long)n*s + s) >> 32);
return q >> k;
}如果你知道 0 ≤ n < 2^31,就像正的有符号整数一样,那么你就不需要担心不同的情况。你可以增加 k 的值一个单位而不必担心 s 溢出。取 N = 31,选择一个 k,使得 2k−1 < d ≤ 2k,并且设置 s = (sN+k+2k−1)/d。那么 n/d = (ns) << (N + k)。
5.10.4 Signed Division by a Constant
我们可以使用与5.10.3节中类似的思想和算法来处理有符号常数。如果d < 0,那么我们可以先除以 |d|,然后在稍后修正符号,所以现在我们假设 d > 0。5.10.3节的第一个数学结果适用于有符号的n。如果 d > 0 并且 2N+k < ds ≤ 2N+k + 2k,那么

对于32位有符号的n,我们取N = 31,并选择k ≤ 31,使得2k−1 < d ≤ 2k。这确保了我们可以找到一个32位无符号整数 s = (2N+k + 2k )/d,满足前面的关系式。我们需要特别注意将32位有符号n与32位无符号s相乘。我们使用带有修正的带符号长整型乘法实现这一点,如果s的最高位设置了,就进行修正。
例子5.15
以下例程sdiv_by_const展示了如何除以一个有符号常数d。在实际应用中,你将在编译时预先计算k和s。只有针对你特定d值的涉及n的操作需要在运行时执行。
int sdiv_by_const(int n, int d)
{
int s,k,q;
unsigned int D;
/* set D to be the absolute value of d, we assume d!=0 */
if (d>0)
{
D=(unsigned int)d; /* 1 <= D <= 0x7FFFFFFF */
}
else
{
D=(unsigned int) - d; /* 1 <= D <= 0x80000000 */
}
/* first find k such that (1 << k) <= D < (1 << (k+1)) */
for (k=0; D/2>=(1u << k); k++);
if (D==1u << k)
{
/* we can implement the divide with a shift */
q = n >> 31; /* 0 if n>0, -1 if n<0 */
q=n+ ((unsigned)q >> (32-k)); /* insert rounding */
q = q >> k; /* divide */
if (d < 0)
{
q = -q;
/* correct sign */
}
return q;
}
/* Next find s in the range 0<=s<=0xFFFFFFFF */
/* Note that k here is one smaller than the k in the equation */
s = (int)(((1ull << (31+(k+1)))+(1ull << (k+1)))/D);
if (s>=0)
{
q = (int)(((signed long long)n*s) >> 32);
}
else
{
/* (unsigned)s = (signed)s + (1 << 32) */
q=n+ (int)(((signed long long)n*s) >> 32);
}
q = q >> k;
/* if n<0 then the formula requires us to add one */
q += (unsigned)n >> 31;
/* if d was negative we must correct the sign */
if (d<0)
{
q = -q;
}
return q;
}第7.3节展示了如何在汇编语言中高效实现除法。
总结除法:
- 尽量避免使用除法。不要将其用于循环缓冲处理。
- 如果无法避免除法,尝试利用除法算法通常同时生成商 n/d 和余数 n%d 的特点。
- 要重复使用相同的分母 d 进行除法运算,可以事先计算 s = (2k − 1)/d。这样,可以用 s 的2k位乘法来代替将一个 k 位无符号整数除以 d。
- 要将小于 2N 的无符号整数 n 除以无符号常数 d,可以找到一个32位无符号整数 s,并进行位移操作,使得 n/d 可以表示为 (ns) << (N + k) 或者 (ns + s) << (N + k)。具体的选择取决于 d。对于有符号除法也有类似的结果。
5.11 Floating Point
大多数ARM处理器实现不提供硬件浮点支持,在价格敏感的嵌入式应用中使用ARM可以节省功耗和面积。除了在ARM7500FE上使用的浮点加速器(FPA)和矢量浮点加速器(VFP)硬件之外,C编译器必须提供对软件浮点的支持。
实际上,这意味着C编译器将每个浮点操作转换为子程序调用。C库包含用整数算术模拟浮点行为的子例程。该代码是用高度优化的汇编语言编写的。
即使如此,浮点算法的执行速度也远远慢于相应的整数算法。
如果您需要快速执行和分数值,应该使用定点或块浮点算法。分数值在处理音频和视频等数字信号时经常使用。这是一个庞大而重要的编程领域,所以我们把一整章,第8章,专门用于介绍ARM上的数字信号处理领域。
为了获得最佳性能,您需要用汇编语言编写算法(请参考第8章的示例)。
5.12 Inline Functions and Inline Assembly
第5.5节介绍了如何高效地调用函数。您可以通过内联函数完全消除函数调用开销。此外,许多编译器允许在C源代码中包含内联汇编。使用包含汇编指令的内联函数,您可以让编译器支持通常不可用的ARM指令和优化。本节的示例将使用armcc中的内联汇编器。请不要将内联汇编器与主汇编器armasm或gas混淆。内联汇编器是C编译器的一部分。C编译器仍然执行寄存器分配、函数入口和出口。编译器还尝试优化您编写的内联汇编代码,或者在调试模式下进行反优化。尽管编译器的输出在功能上等同于您的内联汇编,但可能并非完全相同。
内联函数和内联汇编的主要好处是使得C语言能够访问通常不可用的操作。与#define宏相比,最好使用内联函数,因为后者不检查函数参数和返回值的类型。
以一个示例来说明,许多语音处理算法使用到饱和乘积双累加原语。该操作针对16位有符号操作数x和y以及32位累加器a计算a + 2xy。此外,如果操作结果超过32位范围,所有操作都会饱和到最接近的有效值。我们称x和y为Q15固定点整数,因为它们分别表示x2-15和y2-15的值。同样,a是Q31固定点整数,因为它表示a2-31的值。
我们可以使用内联函数qmac来定义这个新操作:
__inline int qmac(int a, int x, int y)
{
int i;
i = x*y; /* this multiplication cannot saturate */
if (i>=0)
{
/* x*y is positive */
i = 2*i;
if (i<0)
{
/* the doubling saturated */
i = 0x7FFFFFFF;
}
if (a + i < a)
{
/* the addition saturated */
return 0x7FFFFFFF;
}
return a + i;
}
/* x*y is negative so the doubling can’t saturate */
if (a + 2*i > a)
{
/* the accumulate saturated */
return - 0x80000000;
}
return a + 2*i;
}现在我们可以使用这个新操作来计算一个饱和相关性。换句话说,我们可以计算带有饱和的 a = 2x0y0 +···+ 2xN−1yN−1。
int sat_correlate(short *x, short *y, unsigned int N)
{
int a=0;
do
{
a = qmac(a, *(x++), *(y++));
} while (--N);
return a;
}编译器将每个qmac函数调用替换为内联代码。换句话说,它会插入qmac的代码而不是调用qmac。我们C实现的qmac并不是非常高效,需要几个if语句。我们可以使用汇编语言更高效地编写它。C编译器中的内联汇编器允许我们在内联C函数中使用汇编语言。
示例5.16展示了使用内联汇编的qmac的高效实现。该示例支持armcc和gcc的内联汇编格式,这两种格式有相当大的差异。在gcc格式中,"cc"告诉编译器该指令读取或写入条件码标志位。请参阅armcc或gcc手册获取更多信息。
__inline int qmac(int a, int x, int y)
{
int i;
const int mask = 0x80000000;
i = x*y;
#ifdef __ARMCC_VERSION /* check for the armcc compiler */
__asm
{
ADDS i, i, i
/* double */
EORVS i, mask, i, ASR 31 /* saturate the double */
ADDS a, a, i
/* accumulate */
EORVS a, mask, a, ASR 31 /* saturate the accumulate */
}
#endif
#ifdef __GNUC__ /* check for the gcc compiler */
asm("ADDS % 0, % 1, % 2 ":"=r" (i):"r" (i) ,"r" (i):"cc");
asm("EORVS % 0, % 1, % 2,ASR#31":"=r" (i):"r" (mask),"r" (i):"cc");
asm("ADDS % 0, % 1, % 2 ":"=r" (a):"r" (a) ,"r" (i):"cc");
asm("EORVS % 0, % 1, % 2,ASR#31":"=r" (a):"r" (mask),"r" (a):"cc");
#endif
return a;
}这个内联代码将sat_correlate的主循环从19条指令减少到9条指令。 示例5.17 假设我们使用带有ARMv5E扩展的ARM9E处理器。我们可以再次重写qmac,以便编译器使用新的ARMv5E指令:
__inline int qmac(int a, int x, int y)
{
int i;
__asm
{
SMULBB i, x, y /* multiply */
QDADD a, a, i /* double + saturate + accumulate + saturate */
}
return a;
}这次主循环编译为仅六条指令:
sat_correlate_v3
STR r14,[r13,#-4]! ; stack lr
MOV r12,#0
;a=0
sat_v3_loop
LDRSH r3,[r0],#2 ; r3 = *(x++)
LDRSH r14,[r1],#2 ; r14 = *(y++)
SUBS r2,r2,#1 ; N-- and set flags
SMULBB r3,r3,r14 ; r3 = r3 * r14
QDADD r12,r12,r3 ; a = sat(a+sat(2*r3))
BNE sat_v3_loop ; if (N!=0) goto loop
MOV r0,r12 ; r0 = a
LDR pc,[r13],#4 ; return r0其他通常无法从C语言中使用的指令包括协处理器指令。示例5.18展示了如何访问这些指令。
示例5.18向协处理器15写入以刷新指令缓存。您可以使用类似的代码来访问其他协处理器编号。
void flush_Icache(void)
{
#ifdef __ARMCC_VERSION /* armcc */
__asm {MCR p15, 0, 0, c7, c5, 0}
#endif
#ifdef __GNUC__ /* gcc */
asm ( "MCR p15, 0, r0, c7, c5, 0" );
#endif
}总结:内联函数和汇编语言
■ 使用内联函数来声明C编译器不支持的新操作或原语。
■ 使用内联汇编来访问C编译器不支持的ARM指令,例如协处理器指令或ARMv5E扩展指令。
5.13 Portability Issues
下面是将C代码移植到ARM时可能遇到的一些问题的总结:
■ char类型:在ARM上,char类型是无符号的,而不是像其他许多处理器那样有符号。一个常见的问题涉及使用char类型的循环计数器i和终止条件i ≥ 0,它们会变成无限循环。在这种情况下,armcc编译器会产生一个"unsigned comparison with zero"的警告。您可以选择使用编译器选项将char类型设置为有符号,或者将循环计数器改为int类型。
//现在不一定,要看编译器
■ int类型:一些旧的架构使用16位的int类型,在转换为ARM的32位int类型时可能会引起问题,尽管这种情况现在很少见。请注意,表达式在计算之前会被提升为int类型。因此,如果i = -0x1000,在16位机器上,表达式i == 0xF000为真,但在32位机器上为假。
■ 不对齐的数据指针:某些处理器支持从不对齐地址加载short和int类型的值。C程序可能直接操作指针,使它们变得不对齐,例如将char*转换为int*。直到ARMv5TE,ARM架构不支持不对齐指针。要检测它们,请在配置了对齐检查陷阱的ARM上运行程序。例如,您可以配置ARM720T在访问不对齐时发生数据中止。
■ 字节序假设:C代码可能对内存系统的字节序做出假设,例如将char*转换为int*。如果您将ARM配置为与代码所期望的字节序相同,那么就没有问题。否则,您必须删除依赖于字节序的代码片段,并用与字节序无关的代码替换它们。有关更多详细信息,请参阅第5.9节。
■ 函数原型:armcc编译器将参数以狭窄(narrow)方式传递,即缩小到参数类型的范围。如果函数的原型不正确,那么函数可能返回错误的结果。其他将参数以宽的方式传递的编译器,即使函数原型不正确,也可能给出正确的答案。始终使用ANSI原型。
■ 位字段的使用:位字段内的位布局取决于具体实现和字节序。如果C代码假设位按照特定顺序布局,那么这段代码就不具备可移植性。
■ 枚举的使用:尽管枚举是可移植的,不同的编译器会为枚举分配不同数量的字节。gcc编译器将始终为enum类型分配四个字节。armcc编译器只有在枚举值仅为八位时才分配一个字节。因此,如果在API结构中使用枚举,则无法在不同编译器之间交叉链接代码和库。
■ 内联汇编:在C代码中使用内联汇编会降低不同体系结构之间的可移植性。您应该将任何内联汇编分离为小的内联函数,以便于替换。此外,还可以提供参考的纯C实现这些函数的方法,在其他体系结构上可以使用。
■ volatile关键字:在ARM的内存映射外设位置的类型定义中使用volatile关键字。此关键字防止编译器优化内存访问,并确保编译器生成正确类型的数据访问。例如,如果将内存位置定义为volatile short类型,那么编译器将使用16位的加载和存储指令LDRSH和STRH来访问它。
5.14 Summary
通过以一定的方式编写C例程,您可以帮助C编译器生成更快的ARM代码。性能关键的应用程序通常包含一些主导性能的例程;在重写这些例程时,请遵循本章的指导原则。
以下是我们涵盖的关键性能要点:
■ 对于局部变量、函数参数和返回值,请使用有符号和无符号的int类型。这样可以避免强制转换,并有效地使用ARM的本机32位数据处理指令。
■ 最高效的循环形式是向零计数的do-while循环。
■ 展开重要的循环以减少循环开销。
■ 不要依赖编译器来优化重复的内存访问。指针别名通常会阻止这种优化。
■ 尽量将函数的参数限制为四个。如果参数保存在寄存器中,函数调用速度更快。
■ 结构体按元素大小递增的顺序布局,特别是在编译为Thumb指令时。
■ 不要使用位字段,而是使用掩码和逻辑操作。
■ 避免使用除法,可以使用倒数的乘法代替。
■ 避免使用不对齐的数据。如果数据可能不对齐,请使用char*指针类型。
■ 使用C编译器中的内联汇编来访问C编译器不支持的指令或优化。
Chapter6 Writing and Optimizing ARM Assembly Code
嵌入式软件项目通常包含几个主导系统性能的关键子例程。通过优化这些例程,您可以降低系统功耗,并减少实时操作所需的时钟速度。优化可以将一个不可行的系统变为可行的系统,或将一个竞争力不强的系统变为有竞争力的系统。
如果您按照第5章中给出的规则仔细编写C代码,您将获得一个相对高效的实现。为了实现最大性能,您可以使用手写汇编语言来优化关键的例程。手动编写汇编语言使您直接控制了三种优化工具,这些工具无法通过编写C源代码显式使用:
■ 指令调度:重新排列代码序列中的指令,以避免处理器停顿。由于ARM实现是流水线的,一条指令的执行时间可能会受到相邻指令的影响。我们将在第6.3节中详细讨论这个问题。
■ 寄存器分配:决定如何将变量分配到ARM寄存器或栈位置,以实现最大性能。我们的目标是尽量减少内存访问次数。请参阅第6.4节。
■ 条件执行:利用ARM的全部条件码和条件指令范围。请参阅第6.5节。
优化汇编例程需要额外的工作量,因此不要费力去优化非关键的例程。当您花时间对一个例程进行优化时,它带来的副作用是让您更好地理解算法、瓶颈和数据流。
第6.1节介绍了在ARM上进行汇编编程的基础知识。它向您展示了如何用汇编函数替换C函数,然后可以对该函数进行性能优化。
我们将介绍一些常见的优化技术,特别适用于ARM汇编语言编写。虽然本章没有专门涵盖Thumb汇编语言,因为在32位总线可用时,ARM汇编语言总是可以获得更好的性能。Thumb对于减小对性能关键性不大的C代码的编译大小以及在16位数据总线上高效执行非常有用。这里介绍的许多原则同样适用于Thumb和ARM。
对于您的目标硬件所使用的ARM核心,特别是信号处理(在第8章中有详细介绍),最佳优化方法可能会有所不同。然而,您通常可以编写一个在所有ARM实现中都相对高效的例程。为了保持一致性,本章在示例中使用ARM9TDMI优化和周期计数。然而,这些示例在从ARM7TDMI到ARM10E的所有ARM核心上都能高效运行。
6.1 Writing Assembly Code
这一节提供了一些示例,展示了如何编写基本的汇编代码。我们假设您已经熟悉第3章中介绍的ARM指令;完整的指令参考可以在附录A中找到。我们还假设您已经熟悉第5.4节中介绍的ARM和Thumb过程调用标准。
和本书的其他部分一样,本章使用ARM宏汇编器armasm来进行示例(有关armasm语法和参考,请参阅附录A中的第A.4节)。您也可以使用GNU汇编器gas(有关GNU汇编器语法的详细信息,请参阅第A.5节)。
示例6.1展示了如何将一个C函数转换为一个汇编函数,这通常是汇编优化的第一步。考虑以下简单的C程序main.c,它打印从0到9的整数的平方:
#include <stdio.h>
int square(int i);
int main(void)
{
int i;
for (i=0; i<10; i++)
{
printf("Square of %d is %d\n", i, square(i));
}
}
int square(int i)
{
return i*i;
}让我们看看如何用执行相同操作的汇编函数来替换`square`函数。删除`square`的C定义,但保留声明(第二行),生成一个新的C文件`main1.c`。然后,添加一个名为`square.s`的armasm汇编器文件,内容如下所示:
AREA |.text|, CODE, READONLY
EXPORT square
; int square(int i)
square
MUL r1, r0, r0 ; r1 = r0 * r0
MOV r0, r1 ; r0 = r1
MOV pc, lr ; return r0
END`AREA`指令用于为代码所在的区域或代码段命名。如果在符号或区域名中使用非字母数字字符,则需要用竖线括起来。否则,许多非字母数字字符将具有特殊含义。在上面的代码中,我们定义了一个名为`.text`的只读代码区域。
`EXPORT`指令使得符号`square`可以用于外部链接。在第六行,我们将符号`square`定义为代码标签。注意,armasm将非缩进的文本视为标签定义。
当调用`square`函数时,参数传递由ATPCS(请参见第5.4节)定义。输入参数通过寄存器r0传递,返回值则通过寄存器r0返回。乘法指令有一个限制,即目标寄存器不能与第一个参数寄存器相同。因此,我们将乘法的结果放入r1,并将其移动到r0。
`END`指令标记汇编文件的结束。分号后面的内容是注释。
下面的脚本演示了如何使用命令行工具构建这个示例:
armcc -c main1.c
armasm square.s
armlink -o main1.axf main1.o square.o示例6.1仅在将C编译为ARM代码时才起作用。如果将C编译为Thumb代码,则汇编例程必须使用BX指令返回。
示例6.2展示了在将C编译为Thumb代码时调用ARM代码所需的唯一更改,即将返回指令改为BX。BX指令根据lr的第0位返回到ARM或Thumb状态。因此,该例程可以从ARM或Thumb中调用。只要处理器支持BX(ARMv4T及更高版本),就应该使用BX lr而不是MOV pc, lr。创建一个名为square2.s的新汇编文件,内容如下所示:
AREA |.text|, CODE, READONLY
EXPORT square
; int square(int i)
square
MUL r1, r0, r0 ; r1 = r0 * r0
MOV r0, r1 ; r0 = r1
BX lr
; return r0
END使用这个例子,我们使用Thumb C编译器tcc来构建C文件。我们使用启用了交互工作标志的汇编文件进行汇编,以便链接器允许Thumb C代码调用ARM汇编代码。您可以使用以下命令来构建这个例子:
tcc -c main1.c
armasm -apcs /interwork square2.s
armlink -o main2.axf main1.o square2.o示例6.3展示了如何从汇编例程中调用子例程。我们将采用示例6.1,并将整个程序(包括main函数)转换为汇编代码。我们将调用C库函数printf作为子例程。创建一个名为main3.s的新汇编文件,内容如下所示:
AREA |.text|, CODE, READONLY
EXPORT main
IMPORT |Lib$$Request$$armlib|, WEAK
IMPORT __main ; C library entry
IMPORT printf ; prints to stdout
i RN 4
; int main(void)
main
STMFD sp!, {i, lr}
MOV i, #0
loop
ADR r0, print_string
MOV r1, i
MUL r2, i, i
BL printf
ADD i, i, #1
CMP i, #10
BLT loop
LDMFD sp!, {i, pc}
print_string
DCB "Square of %d is %d\n", 0
END我们使用了一个新的指令IMPORT,来声明在其他文件中定义的符号。导入的符号Lib$$Request$$armlib是一个请求,要求链接器与标准ARM C库进行链接。WEAK修饰符可以防止链接器在找不到该符号时报错。如果找不到该符号,它的值将为零。第二个导入的符号___main是C库初始化代码的起始位置。只有在定义自己的main函数时才需要导入这些符号;在C代码中定义的main函数会自动导入这些符号。导入printf允许我们调用C库函数。
RN指令允许我们为寄存器使用名称。在本例中,我们将寄存器r4定义为i的替代名称。使用寄存器名称使得代码更易读。而且,在以后更改变量分配到寄存器上时更加方便。
请注意,ATPCS规定函数必须保存寄存器r4到r11和sp。我们破坏了i(r4),调用printf会破坏lr。因此,我们在函数开始处使用STMFD指令将这两个寄存器保存在堆栈中。LDMFD指令从堆栈中取出这些寄存器,并通过将返回地址写入pc来返回。
DCB指令用于定义字节数据,可以是一个字符串或逗号分隔的字节列表。
要构建这个示例,您可以使用以下命令行脚本:
armasm main3.s
armlink -o main3.axf main3.o请注意,示例6.3还假设代码是从ARM代码中调用的。如果代码可以像示例6.2中那样从Thumb代码中调用,那么我们必须能够返回到Thumb代码。对于ARMv5之前的架构,我们必须使用BX指令来返回。将最后一条指令更改为以下两条指令:
LDMFD sp!, {i, lr}
BX lr最后,让我们来看一个传递超过四个参数的示例。回想一下,ATPCS将前四个参数放在寄存器r0到r3中。后续的参数被放置在堆栈上。
示例6.4定义了一个函数sumof,它可以对任意数量的整数进行求和。参数是要求和的整数的数量,后跟整数列表。sumof函数用汇编语言编写,并且可以接受任意数量的参数。将示例的C部分放在名为main4.c的文件中:
#include <stdio.h>
/* N is the number of values to sum in list ... */
int sumof(int N, ...);
int main(void)
{
printf("Empty sum=%d\n", sumof(0));
printf("1=%d\n", sumof(1,1));
printf("1+2=%d\n", sumof(2,1,2));
printf("1+2+3=%d\n", sumof(3,1,2,3));
printf("1+2+3+4=%d\n", sumof(4,1,2,3,4));
printf("1+2+3+4+5=%d\n", sumof(5,1,2,3,4,5));
printf("1+2+3+4+5+6=%d\n", sumof(6,1,2,3,4,5,6));
}接下来,在一个名为sumof.s的汇编文件中定义sumof函数:
AREA |.text|, CODE, READONLY
EXPORT sumof
N RN 0 ; number of elements to sum
sum RN 1 ; current sum
; int sumof(int N, ...)
sumof
SUBS N, N, #1 ; do we have one element
MOVLT sum, #0 ; no elements to sum!
SUBS N, N, #1 ; do we have two elements
ADDGE sum, sum, r2
SUBS N, N, #1 ; do we have three elements
ADDGE sum, sum, r3
MOV r2, sp ; top of stack
loop
SUBS N, N, #1 ; do we have another element
LDMGEFD r2!, {r3} ; load from the stack
ADDGE sum, sum, r3
BGE loop
MOV r0, sum
MOV pc, lr ; return r0
END该代码会保持要求和的剩余值的计数,即N。前三个值存储在寄存器r1、r2、r3中,其余的值存储在堆栈上。您可以使用以下命令来构建这个示例:
armcc -c main4.c
armasm sumof.s
armlink -o main4.axf main4.o sumof.o6.2 Profiling and Cycle Counting
//性能分析与循环计数
优化过程的第一阶段是确定关键的程序段,并测量它们当前的性能。分析器是一种工具,用于测量每个子例程所花费的时间或处理周期的比例。您可以使用分析器来确定最关键的程序段。循环计数器用于测量特定程序段使用的周期数。您可以使用循环计数器在优化前后对给定的子例程进行基准测试,以评估优化效果。
ADS1.1调试器使用的ARM模拟器称为ARMulator,并提供了性能分析和循环计数的功能。ARMulator分析器通过定期采样程序计数器pc来工作。分析器识别pc所指向的函数,并为遇到的每个函数更新一个命中计数器。另一种方法是使用模拟器的跟踪输出作为分析的源数据。
请确保您了解所使用的分析器的工作原理以及其准确性的限制。如果采样数量太少,基于pc采样的分析器可能会产生无意义的结果。您甚至可以使用定时器中断在硬件系统中实现自己的基于pc采样的分析器来收集pc数据点。请注意,定时器中断会减慢您试图测量的系统!
ARM的实现通常不包含循环计数硬件,因此为了便于测量循环计数,您应该使用带有ARM模拟器的ARM调试器。您可以配置ARMulator来模拟各种不同的ARM核心,并获得多个平台的循环计数基准测试数据。
6.3 Instruction Scheduling
//指令调度
指令执行所需的时间取决于实现的流水线。在本章中,我们假设使用ARM9TDMI流水线定时。您可以在附录D的D.3节中找到相关信息。以下规则总结了ARM9TDMI上常见指令类别的周期计时:
- 根据cpsr中的ARM条件码进行条件判断的指令,如果条件不满足,则执行需要一个周期。如果条件满足,则遵循以下规则:
- 包括立即数移位在内的ALU操作(如加法、减法和逻辑操作)需要一个周期。如果使用寄存器指定的移位,则需要再增加一个周期。如果指令写入pc寄存器,则增加两个周期。
- 加载指令(如LDR和LDM)用于加载N个32位字的内存数据,发出指令需要N个周期,但最后一个加载的字的结果在下一个周期不可用。更新的加载地址在下一个周期可用。这里假设在无缓存系统中存在零等待状态的内存,或者在有缓存系统中存在缓存命中。加载单个值的LDM是例外情况,需要两个周期。如果指令加载pc寄存器,则增加两个周期。
- 加载16位或8位数据的指令(如LDRB、LDRSB、LDRH和LDRSH)发出指令需要一个周期。加载结果在接下来的两个周期内不可用(如下LS1/LS2)。更新的加载地址在下一个周期可用。这里假设在无缓存系统中存在零等待状态的内存,或者在有缓存系统中存在缓存命中。
- 分支指令需要三个周期。
- 存储指令(如STR和STM)存储N个值需要N个周期。这里假设在无缓存系统中存在零等待状态的内存,或者在有缓存系统中存在缓存命中或具有N个空闲条目的写缓冲区。存储单个值的STM是例外情况,需要两个周期。
- 乘法指令的执行周期数取决于乘积中第二个操作数的值(请参阅附录D的表格D.6)。
根据ARM9TDMI流水线的定时规则,不同的指令类别需要不同数量的周期来完成执行。这些周期计时信息对于优化代码的性能很有帮助。
要了解如何在ARM上高效地安排代码,我们需要了解ARM流水线和依赖关系。ARM9TDMI处理器并行执行五个操作:
■ 获取(Fetch):从内存中获取地址为pc处的指令。该指令被加载到核心并按顺序流经核心管道。
■ 解码(Decode):解码上一个周期获取的指令。如果某些输入操作数无法通过任何转发路径获得,则处理器也会从寄存器库中读取它们。
■ ALU:运行上一个周期解码的指令。请注意,该指令最初从地址pc-8(ARM状态)或pc-4(Thumb状态)处获取。通常,这涉及计算数据处理操作的答案或加载、存储、分支操作的地址。一些指令可能在此阶段花费多个周期。例如,乘法和寄存器控制移位操作需要多个ALU周期。
■ LS1:加载或存储由加载或存储指令指定的数据。如果该指令不是加载或存储指令,则该阶段不起作用。
■ LS2:提取并对通过字节或半字加载指令加载的数据进行零扩展或符号扩展。如果该指令不是8位字节或16位半字项的加载指令,则该阶段没有影响。
//ARM9TDMI属于ARMv4系列。

图6.1显示了五级ARM9TDMI流水线的简化功能视图。请注意,乘法和寄存器移位操作未在图中显示。在指令完成五个流水线阶段后,核心将结果写入寄存器文件。请注意,pc指向正在获取的指令的地址。 ALU同时执行从地址pc-8最初获取的指令和从地址pc处获取的指令。
流水线如何影响指令的时间?考虑以下示例。这些示例显示了由于早期指令必须在当前指令可以向下流水线之前完成某个阶段而导致的周期计时方式的更改。
要计算代码块需要多少个周期,请使用附录D中总结一系列ARM内核的周期计时和互锁周期的表格。
如果某条指令需要前一条指令的结果但其结果并不可用,则处理器会暂停运行,这被称为流水线危险或流水线互锁。
例6.5
该示例显示了没有互锁的情况。
ADD r0, r0, r1
ADD r0, r0, r2这个指令对需要两个周期。ALU在一个周期内计算r0 + r1。因此,在第二个周期中,ALU可以使用r0 + r1的结果来计算r0 + r2。
例6.6
该示例显示了由加载-使用引起的一次互锁,需要一个周期。
LDR r1, [r2, #4]
ADD r0, r0, r1这个指令对需要三个周期。在第一个周期中,ALU计算地址r2 + 4,同时并行解码ADD指令。然而,在第二个周期中,ADD指令无法进行,因为加载指令尚未加载r1的值。因此,流水线会在加载指令完成LS1阶段期间暂停一个周期。现在r1已准备好,处理器在第三个周期中执行ALU中的ADD指令。

图6.2说明了这种互锁如何影响流水线。处理器将ADD指令在流水线的ALU阶段暂停一个周期,而加载指令完成LS1阶段。我们用斜体的ADD表示这个停顿。由于LDR指令继续向下流水线,但ADD指令被阻塞,它们之间出现了间隙。这个间隙有时被称为流水线气泡。我们用破折号标记了这个气泡。
例6.7
该示例显示了由延迟加载使用引起的一次互锁,需要一个周期。
LDRB r1, [r2, #1]
ADD r0, r0, r2
EOR r0, r0, r1这个指令需要四个周期。虽然ADD在加载字节后的一个周期进行,但是EOR指令无法在第三个周期开始。直到加载指令完成流水线的LS2阶段,r1值才准备好。处理器将EOR指令暂停一个周期。

请注意,ADD指令根本不影响时间。无论是否存在该序列,该序列都需要四个周期!图6.3显示了该序列如何通过处理器流水线进行。由于ADD不使用加载的结果r1,因此ADD不会导致任何停顿。
例6.8
该示例展示了为什么分支指令需要三个周期。当跳转到一个新地址时,处理器必须清空流水线。
MOV r1, #1
B case1
AND r0, r0, r1
EOR r2, r2, r3
...
case1
SUB r0, r0, r1这三条执行的指令共需要五个周期。MOV指令在第一个周期执行。在第二个周期,分支指令计算目标地址。这导致核心清空流水线,并使用新的PC值重新填充流水线。重新填充需要两个周期。最后,SUB指令正常执行。图6.4说明了每个周期的流水线状态。当分支发生时,流水线会丢弃分支后面的两条指令。
6.3.1 Scheduling of load instructions
加载指令在编译代码中经常出现,约占所有指令的三分之一。仔细调度加载指令,以避免流水线停顿可以提高性能。编译器会尽力对代码进行调度,但是我们在5.6节中所看到的C语言的别名问题限制了可用的优化。编译器不能将加载指令移到存储指令之前,除非它确定所使用的两个指针不指向同一个地址。
让我们考虑一个内存密集型任务的例子。下面的函数str_tolower将一个以零结尾的字符字符串从in复制到out,并在此过程中将字符串转换为小写。
void str_tolower(char *out, char *in)
{
unsigned int c;
do
{
c = *(in++);
if (c>=’A’ && c<=’Z’)
{
c=c+ (’a’ -’A’);
}
*(out++) = (char)c;
} while (c);
}ADS1.1编译器生成了以下编译输出。请注意,编译器将条件(c >= 'A' && c <= 'Z')优化为检查0 <= c - 'A' <= 'Z' - 'A'。编译器可以使用单个无符号比较执行此检查。
str_tolower
LDRB r2,[r1],#1 ; c = *(in++)
SUB r3,r2,#0x41 ; r3 = c -‘A’
CMP r3,#0x19 ; if (c <=‘Z’-‘A’)
ADDLS r2,r2,#0x20 ; c +=‘a’-‘A’
STRB r2,[r0],#1 ; *(out++) = (char)c
CMP r2,#0 ; if (c!=0)
BNE str_tolower ; goto str_tolower
MOV pc,r14 ; return不幸的是,SUB指令直接使用加载c的LDRB指令之后的c的值。因此,ARM9TDMI流水线将停顿两个周期。由于之后的所有操作都依赖于加载c的值,编译器无法做出更好的处理。然而,使用汇编语言可以通过改变算法的结构来避免这些周期,我们称这两种方法为预加载和展开。
6.3.1.1 Load Scheduling by Preloading
在这种预加载的方法中,我们在前一个循环结束时加载下一个循环所需的数据,而不是在当前循环开始时加载。为了在增加代码大小很少的情况下提高性能,我们不展开循环。
以下是应用预加载方法到str_tolower函数的汇编示例(Example 6.9):
out RN 0 ; pointer to output string
in RN 1 ; pointer to input string
c RN 2 ; character loaded
t RN 3 ; scratch register
; void str_tolower_preload(char *out, char *in)
str_tolower_preload
LDRB c, [in], #1 ; c = *(in++)
loop
SUB t, c, #’A’ ; t = c-’A’
CMP t, #’Z’-’A’ ; if (t <= ’Z’-’A’)
ADDLS c, c, #’a’-’A’ ; c += ’a’-’A’;
STRB c, [out], #1 ; *(out++) = (char)c;
TEQ c, #0 ; test if c==0
LDRNEB c, [in], #1 ; if (c!=0) { c=*in++;
BNE loop
;
goto loop; }
MOV pc, lr
; return预调度版本的指令长度比C版本多一个,但每个内部循环迭代可以节省两个周期。这将在ARM9TDMI上将每个字符的循环从11个周期减少到9个周期,从而提高了1.22倍的速度。ARM架构特别适合这种类型的预加载,因为指令可以有条件地执行。由于循环i正在加载循环i + 1的数据,始终存在第一个和最后一个循环的问题。对于第一个循环,我们可以在循环开始之前插入额外的加载指令来预加载数据。对于最后一个循环,关键是循环不读取任何数据,否则它将读取超出数组的末尾。这可能导致数据异常!在ARM上,我们可以通过使加载指令有条件地执行来轻松解决这个问题。在Example 6.9中,只有在循环还将迭代一次时,才会发生下一个字符的预加载。在最后一个循环中不进行字节加载。
6.3.1.2 Load Scheduling by Unrolling
这种预加载的方法通过展开循环,然后交错执行循环体来实现。例如,我们可以交错执行循环迭代i、i + 1、i + 2。当循环i中的操作结果尚未准备好时,我们可以执行循环i + 1中的操作,避免等待循环i的结果。
以下是将展开循环应用于str_tolower函数的汇编示例(Example 6.10):
out RN 0 ; pointer to output string
in RN 1 ; pointer to input string
ca0 RN 2 ; character 0
t RN 3 ; scratch register
ca1 RN 12 ; character 1
ca2 RN 14 ; character 2
; void str_tolower_unrolled(char *out, char *in)
str_tolower_unrolled
STMFD sp!, {lr} ; function entry
loop_next3
LDRB ca0, [in], #1 ; ca0 = *in++;
LDRB ca1, [in], #1 ; ca1 = *in++;
LDRB ca2, [in], #1 ; ca2 = *in++;
SUB t, ca0, #’A’ ; convert ca0 to lower case
CMP t, #’Z’-’A’
ADDLS ca0, ca0, #’a’-’A’
SUB t, ca1, #’A’ ; convert ca1 to lower case
CMP t, #’Z’-’A’
ADDLS ca1, ca1, #’a’-’A’
SUB t, ca2, #’A’ ; convert ca2 to lower case
CMP t, #’Z’-’A’
ADDLS ca2, ca2, #’a’-’A’
STRB ca0, [out], #1 ; *out++ = ca0;
TEQ ca0, #0
; if (ca0!=0)
STRNEB ca1, [out], #1 ; *out++ = ca1;
TEQNE ca1, #0
; if (ca0!=0 && ca1!=0)
STRNEB ca2, [out], #1 ; *out++ = ca2;
TEQNE ca2, #0
; if (ca0!=0 && ca1!=0 && ca2!=0)
BNE loop_next3 ; goto loop_next3;
LDMFD sp!, {pc} ; return;在我们目前所看到的实现中,这个循环是最高效的。在ARM9TDMI上,每个字符需要七个周期。这使得str_tolower函数的速度提高了1.57倍。同样,正是ARM指令的条件性质使得这种优化成为可能。我们使用条件指令来避免存储超出字符串末尾的字符。
然而,Example 6.10中的改进也有一些代价。该例程的代码大小超过原始实现的两倍。我们假设您可以读取输入字符串末尾之后的两个字符,但如果字符串正好位于可用RAM的末尾,则可能不成立,因为读取超出末尾将导致数据异常。此外,对于非常短的字符串,性能可能会较慢,因为(1)堆叠lr会导致额外的函数调用开销,(2)该例程可能会处理多达两个字符,然后才发现它们位于字符串末尾之外。
对于应用程序中时间关键的部分,您应该使用展开循环的这种调度方式,前提是您知道数据大小较大。如果在编译时还知道数据的大小,那么可以解决读取超出数组末尾的问题。
总结指令调度:
- ARM核心具有流水线体系结构。流水线可能会延迟某些指令的结果多个周期。如果您在后续指令中使用这些结果作为源操作数,处理器将插入停顿周期,直到该值准备好。
- 在许多实现中,加载和乘法指令的结果会有延迟。您可以参考附录D,了解特定ARM处理器核心的时钟周期和延迟时机。
- 您有两种软件方法可以消除加载指令后的互锁:您可以预加载,使循环i加载循环i + 1的数据,或者您可以展开循环并交错执行循环i和i + 1的代码。
6.4 Register Allocation
//寄存器分配
您可以使用16个可见的ARM寄存器中的14个来存储通用数据。另外两个寄存器是栈指针r13和程序计数器r15。为了使函数符合ATPCS规范,它必须保留寄存器r4到r11的被调用者值。ATPCS还指定堆栈应该是8字节对齐的;因此,如果调用子程序,您必须保持这种对齐。以下是用于需要许多寄存器的优化汇编例程的模板:
routine_name
STMFD sp!, {r4-r12, lr} ; stack saved registers
; body of routine
; the fourteen registers r0-r12 and lr are available
LDMFD sp!, {r4-r12, pc} ; restore registers and return我们在将r12入栈的唯一目的是为了保持堆栈8字节对齐。如果您的例程不调用其他ATPCS例程,则无需将r12入栈。对于ARMv5及以上版本,即使从Thumb代码中调用,也可以使用上述模板。如果您的例程可能被ARMv4T处理器上的Thumb代码调用,请按如下方式修改模板:
routine_name
STMFD sp!, {r4-r12, lr} ; stack saved registers
; body of routine
; registers r0-r12 and lr available
LDMFD sp!, {r4-r12, lr} ; restore registers
BX lr
; return, with mode switch在这一部分中,我们将研究如何为寄存器密集型任务分配变量到寄存器号码,如何使用超过14个局部变量,并如何充分利用可用的14个寄存器。
6.4.1 Allocating Variables to Register Numbers
当您编写汇编例程时,最好从变量的名称开始使用,而不是显式的寄存器号码。这样可以轻松地更改变量到寄存器号码的分配方式。当它们的使用不重叠时,甚至可以使用相同的物理寄存器号码的不同寄存器名称。寄存器名称提高了优化代码的清晰度和可读性。
在大多数情况下,ARM操作在寄存器号码方面是正交的。换句话说,特定的寄存器号码没有特定的作用。如果在例程中交换两个寄存器Ra和Rb的所有出现次数,则该例程的功能不会改变。
但是,有几种情况下寄存器的物理编号很重要:
■ 参数寄存器。ATPCS规范定义将函数的前四个参数放置在寄存器r0到r3中。其他参数放置在堆栈上。返回值必须放置在r0中。
■ 在加载或存储多个寄存器时使用的寄存器。加载和存储多个指令LDM和STM按升序寄存器号码的顺序操作寄存器列表。如果寄存器列表中出现r0和r1,则处理器将始终使用较低的地址加载或存储r0,以此类推。
■ 加载和存储双字。在ARMv5E中引入的LDRD和STRD指令操作具有连续寄存器号码的一对寄存器Rd和Rd + 1。此外,Rd必须是偶数寄存器号码。
在编写汇编代码时,为了示例说明如何分配寄存器,假设我们想要通过k位将一个包含N位的数组向内存上方移动。为简单起见,假设N很大且是256的倍数。还假设 0 ≤ k < 32,并且输入和输出指针是字对齐的。这种操作在处理多精度数字的算术中很常见,我们希望将其乘以2的k次方。它还可用于在不同的位或字节对齐方式之间进行块复制。例如,C库函数memcpy可以使用该例程仅使用字访问来复制字节数组。
C例程shift_bits实现了对N位数据进行简单的k位移位。它返回移位后剩余的k位。
unsigned int shift_bits(unsigned int *out, unsigned int *in,
unsigned int N, unsigned int k)
{
unsigned int carry=0, x;
do
{
x = *in++;
*out++ = (x << k) | carry;
carry = x >> (32-k);
N -= 32;
} while (N);
return carry;
}为了提高效率,显而易见的方法是展开循环,每次处理8个长度为256位的字,这样我们可以使用加载和存储多个操作一次性加载和存储8个字,以达到最大的效率。在考虑寄存器编号之前,我们编写以下汇编代码:
shift_bits
STMFD sp!, {r4-r11, lr} ; save registers
RSB kr, k, #32
; kr = 32-k;
MOV carry, #0
loop
LDMIA in!, {x_0-x_7}
; load 8 words
ORR y_0, carry, x_0, LSL k ; shift the 8 words
MOV carry, x_0, LSR kr
ORR y_1, carry, x_1, LSL k
MOV carry, x_1, LSR kr
ORR y_2, carry, x_2, LSL k
MOV carry, x_2, LSR kr
ORR y_3, carry, x_3, LSL k
MOV carry, x_3, LSR kr
ORR y_4, carry, x_4, LSL k
MOV carry, x_4, LSR kr
ORR y_5, carry, x_5, LSL k
MOV carry, x_5, LSR kr
ORR y_6, carry, x_6, LSL k
MOV carry, x_6, LSR kr
ORR y_7, carry, x_7, LSL k
MOV carry, x_7, LSR kr
STMIA out!, {y_0-y_7} ; store 8 words
SUBS N, N, #256
; N -= (8 words * 32 bits)
BNE loop
; if (N!=0) goto loop;
MOV r0, carry
; return carry;
LDMFD sp!, {r4-r11, pc}现在来看寄存器分配。为了避免输入参数需要移动寄存器,我们可以立即分配寄存器。
out RN 0
in RN 1
N RN 2
k RN 3为了使加载多个操作能够正常工作,我们必须将x0到x7逐渐分配给递增的寄存器编号,以及将y0到y7类似地分配。请注意,在开始y1之前,我们会先完成x0的分配。一般来说,我们可以将xn分配给与yn+1相同的寄存器。因此,分配如下:
x_0 RN 5
x_1 RN 6
x_2 RN 7
x_3 RN 8
x_4 RN 9
x_5 RN 10
x_6 RN 11
x_7 RN 12
y_0 RN 4
y_1 RN x_0
y_2 RN x_1
y_3 RN x_2
y_4 RN x_3
y_5 RN x_4
y_6 RN x_5
y_7 RN x_6我们快要完成了,但是还有一个问题。还剩下两个变量carry和kr,但只剩下一个空闲寄存器lr。当寄存器用完时,有几种可能的解决方法:
■ 减少每个循环中操作的数量,以减少所需的寄存器数量。在这种情况下,我们可以在每个加载多个操作中加载四个字,而不是八个。
■ 使用栈来存储最不常用的值,以释放更多的寄存器。在这种情况下,我们可以将循环计数器N存储在栈上。(有关将寄存器交换到栈的更多详细信息,请参见第6.4.2节。)
■ 更改代码实现以释放更多的寄存器。这是我们在下面考虑的解决方案。(更多示例请参见第6.4.3节。)
通常,我们会多次迭代执行实现和寄存器分配的过程,直到算法适配为可用的14个寄存器。在这种情况下,我们注意到carry值实际上不需要保持在同一个寄存器中!我们可以开始时将carry值分配给y0,然后当x0不再需要时将其移动到y1,以此类推。我们通过将kr分配给lr并重新编码来完成程序,以使carry不再需要。
Example 6.11 以下汇编代码展示了我们最终的shift_bits例程。它使用了所有可用的14个ARM寄存器。
kr RN lr
shift_bits
STMFD sp!, {r4-r11, lr} ; save registers
RSB kr, k, #32
; kr = 32-k;
MOV y_0, #0
; initial carry
loop
LDMIA in!, {x_0-x_7} ; load 8 words
ORR y_0, y_0, x_0, LSL k ; shift the 8 words
MOV y_1, x_0, LSR kr ; recall x_0 = y_1
ORR y_1, y_1, x_1, LSL k
MOV y_2, x_1, LSR kr
ORR y_2, y_2, x_2, LSL k
MOV y_3, x_2, LSR kr
ORR y_3, y_3, x_3, LSL k
MOV y_4, x_3, LSR kr
ORR y_4, y_4, x_4, LSL k
MOV y_5, x_4, LSR kr
ORR y_5, y_5, x_5, LSL k
MOV y_6, x_5, LSR kr
ORR y_6, y_6, x_6, LSL k
MOV y_7, x_6, LSR kr
ORR y_7, y_7, x_7, LSL k
STMIA out!, {y_0-y_7} ; store 8 words
MOV y_0, x_7, LSR kr
SUBS N, N, #256
; N -= (8 words * 32 bits)
BNE loop
; if (N!=0) goto loop;
MOV r0, y_0
; return carry;
LDMFD sp!, {r4-r11, pc}6.4.2 Using More than 14 Local Variables
如果在例程中需要超过14个32位本地变量,那么必须将一些变量存储在堆栈上。标准的处理过程是从算法最内层的循环开始向外工作,因为最内层的循环具有最大的性能影响。
Example 6.12展示了三个嵌套循环,每个循环都需要从其周围的循环继承的状态信息。(有关循环结构的更多想法和示例,请参见第6.6节。)
nested_loops
STMFD sp!, {r4-r11, lr}
; set up loop 1
loop1
STMFD sp!, {loop1 registers}
; set up loop 2
loop2
STMFD sp!, {loop2 registers}
; set up loop 3
loop3
; body of loop 3
B{cond} loop3
LDMFD sp!, {loop2 registers}
; body of loop 2
B{cond} loop2
LDMFD sp!, {loop1 registers}
; body of loop 1
B{cond} loop1
LDMFD sp!, {r4-r11, pc}当使用示例6.12中的结构时,您可能会发现内层循环的寄存器不足,这时需要将内层循环的变量置换到堆栈中。由于如果使用数字作为堆栈地址偏移量,汇编代码非常难以维护和调试,所以汇编器提供了自动分配变量到堆栈的过程。
Example 6.13展示了如何使用ARM汇编器指令MAP(别名∧)和FIELD(别名#)在处理器堆栈上定义和分配变量和数组的空间。该指令类似于C语言中的struct操作符。
MAP 0 ; map symbols to offsets starting at offset 0
a FIELD 4 ; a is 4 byte integer (at offset 0)
b FIELD 2 ; b is 2 byte integer (at offset 4)
c FIELD 2 ; c is 2 byte integer (at offset 6)
d FIELD 64 ; d is an array of 64 characters (at offset 8)
length FIELD 0 ; length records the current offset reached
example
STMFD sp!, {r4-r11, lr} ; save callee registers
SUB sp, sp, #length ; create stack frame
; ...
STR r0, [sp, #a]
; a = r0;
LDRSH r1, [sp, #b] ; r1 = b;
ADD r2, sp, #d ; r2 = &d[0]
; ...
ADD sp, sp, #length ; restore the stack pointer
LDMFD sp!, {r4-r11, pc} ; return6.4.3 Making the Most of Available Registers
在像ARM这样的加载存储架构中,相对于内存中保存的值,访问寄存器中保存的值更加高效。有几种技巧可以将多个小于32位长度的变量装入一个32位寄存器中,从而减小代码大小并提高性能。本节介绍了三个示例,展示了如何将多个变量打包到一个ARM寄存器中。
示例6.14假设我们希望通过可编程增量遍历数组。常见的例子是以不同的速率遍历音频样本以产生不同音高的音符。我们可以使用以下C代码来表达这个过程:
sample = table[index];
index += increment;通常索引(index)和增量(increment)的值都小到可以使用16位来保存。我们可以将这两个变量打包到一个32位的变量indinc中:

这段C代码可以转换成汇编代码,并使用单个寄存器来保存indinc的值:
LDRB sample, [table, indinc, LSR#16] ; table[index]
ADD indinc, indinc, indinc, LSL#16 ; index+=increment请注意,如果索引(index)和增量(increment)是16位的值,将索引放在indinc的高16位中可以正确实现16位的循环。换句话说,index = (short)(index + increment)。如果您在使用一个循环缓冲区时需要从末尾回到开头(通常称为循环缓冲区),这将非常有用。
示例6.15说明了如何使用一个寄存器来表示移位数量,并结合循环计数器来将一个包含40个元素的数组向右移动shift位。我们定义了一个新的变量cntshf,它将count和shift组合在一起:

out RN 0 ; address of the output array
in RN 1 ; address of the input array
cntshf RN 2 ; count and shift right amount
x RN 3 ; scratch variable
; void shift_right(int *out, int *in, unsigned shift);
shift_right
ADD cntshf, cntshf, #39 << 8 ; count = 39
shift_loop
LDR x, [in], #4
SUBS cntshf, cntshf, #1 << 8 ; decrement count
MOV x, x, ASR cntshf ; shift by shift
STR x, [out], #4
BGE shift_loop
; continue if count>=0
MOV pc, lr示例6.16
如果您处理的是8位或16位值的数组,有时可以通过将多个值打包到单个32位寄存器中来一次性处理多个值。这称为单指令多数据(SIMD)处理。
ARMv5及其之前的ARM架构版本不直接支持SIMD操作。然而,在某些情况下仍然可以实现SIMD类型的紧凑性。第6.6节展示了如何将多个循环值存储在单个寄存器中。这里我们介绍一个图形处理的示例,演示如何使用常规的ADD和MUL指令来处理图像中的多个8位像素,以实现一些SIMD操作。
假设我们想要合并两个图像X和Y以生成一个新图像Z。分别用xn、yn和zn表示这些图像中第n个8位像素。假设0 ≤ a ≤ 256是一个缩放因子。为了合并这些图像,我们设置:
![]()
换句话说,图像Z是将图像X的强度按照 a/256 缩放后与图像Y按照 1 - (a/256) 缩放后相加得到的。请注意:
![]()
因此,每个像素需要进行减法、乘法、移位相加和右移操作。为了一次处理多个像素,我们使用字加载指令一次性加载四个像素。我们使用括号表示法来表示多个值打包到同一个字中:

然后,我们使用与掩码寄存器的AND操作将8位数据解包并提升为16位数据。我们使用如下的表示法:

请注意,即使对于有符号的值 [a,b] + [c,d] = [a + b,c + d],如果我们使用数学方程 a216 + b 来解释 [a,b]。因此,我们可以使用常规算术指令对这些值执行SIMD操作。
下面的代码展示了如何使用只有两个乘法来一次处理四个像素。该代码假定一个大小为176×144的QCIF图像。
IMAGE_WIDTH EQU 176 ; QCIF width
IMAGE_HEIGHT EQU 144 ; QCIF height
pz RN 0 ; pointer to destination image (word aligned)
px RN 1 ; pointer to first source image (word aligned)
py RN 2 ; pointer to second source image (word aligned)
a RN 3 ; 8-bit scaling factor (0-256)
xx RN 4 ; holds four x pixels [x3, x2, x1, x0]
yy RN 5 ; holds four y pixels [y3, y2, y1, y0]
x RN 6 ; holds two expanded x pixels [x2, x0]
y RN 7 ; holds two expanded y pixels [y2, y0]
z RN 8 ; holds four z pixels [z3, z2, z1, z0]
count RN 12 ; number of pixels remaining
mask RN 14 ; constant mask with value 0x00ff00ff
; void merge_images(char *pz, char *px, char *py, int a)
merge_images
STMFD sp!, {r4-r8, lr}
MOV count, #IMAGE_WIDTH*IMAGE_HEIGHT
LDR mask, =0x00FF00FF ; [ 0, 0xFF, 0, 0xFF ]
merge_loop
LDR xx, [px], #4 ; [ x3, x2, x1, x0 ]
LDR yy, [py], #4 ; [ y3, y2, y1, y0 ]
AND x, mask, xx ; [ 0, x2, 0, x0 ]
AND y, mask, yy ; [ 0, y2, 0, y0 ]
SUB x, x, y
; [ (x2-y2), (x0-y0) ]
MUL x, a, x
; [ a*(x2-y2), a*(x0-y0) ]
ADD x, x, y, LSL#8 ; [ w2, w0 ]
AND z, mask, x, LSR#8 ; [ 0, z2, 0, z0 ]
AND x, mask, xx, LSR#8 ; [ 0, x3, 0, x1 ]
AND y, mask, yy, LSR#8 ; [ 0, y3, 0, y1 ]
SUB x, x, y
; [ (x3-y3), (x1-y1) ]
MUL x, a, x
; [ a*(x3-y3), a*(x1-y1) ]
ADD x, x, y, LSL#8 ; [ w3, w1 ]
AND x, mask, x, LSR#8 ; [ 0, z3, 0, z1 ]
ORR z, z, x, LSL#8 ; [ z3, z2, z1, z0 ]
STR z, [pz], #4 ; store four z pixels
SUBS count, count, #4
BGT merge_loop
LDMFD sp!, {r4-r8, pc}
因此,通过分别取最高位和最低位的16位部分,可以轻松将值 [w2,w0] 分离为 w2 和 w0。我们成功地使用32位的加载、存储和数据操作一次处理了四个8位像素,以并行方式执行操作。
总结 寄存器分配:
■ ARM有14个可用于通用目的的寄存器:r0到r12和r14。栈指针r13和程序计数器r15不能用于通用数据。操作系统中断通常假设用户模式下的r13指向一个有效的堆栈,因此不要试图重新使用r13。
■ 如果需要超过14个局部变量,请将变量转移到堆栈上,从最内层循环向外工作。
■ 在编写汇编程序时,使用寄存器名称而不是物理寄存器号码。这样可以更容易重新分配寄存器并维护代码。
■ 为了减轻寄存器压力,有时可以将多个值存储在同一个寄存器中。例如,可以将循环计数器和位移存储在同一个寄存器中。还可以将多个像素存储在一个寄存器中。
6.5 Conditional Execution
处理器核心可以有条件地执行大多数ARM指令。这种条件执行基于15个条件码之一。如果不指定条件,汇编器默认为始终执行条件(AL)。其他14个条件分为七对互补条件。条件依赖于存储在cpsr寄存器中的四个条件码标志N、Z、C、V。请参见附录A中的表A.2,了解可能的ARM条件的列表。还请参阅2.2.6节和3.8节,了解条件执行的介绍。默认情况下,ARM指令不会更新ARM cpsr中的N、Z、C、V标志。对于大多数指令,要更新这些标志,需要在指令助记符后附加一个S后缀。例外是不写入目标寄存器的比较指令。它们唯一的目的是更新标志,因此不需要S后缀。通过结合条件执行和条件设置标志,您可以实现不需要分支的简单if语句。这提高了效率,因为分支可能需要很多周期,并且减少了代码大小。
示例6.17:
以下C代码将无符号整数0 ≤ i ≤ 15转换为十六进制字符c:
if (i<10)
{
c=i+ ‘0’;
}
else
{
c=i+ ‘A’-10;
}我们可以使用条件执行而不是条件分支来将其写成汇编代码:
CMP i, #10
ADDLO c, i, #‘0’
ADDHS c, i, #‘A’-10该序列有效,因为第一个ADD不会改变条件码。第二个ADD仍然取决于比较的结果而进行条件执行。6.3.1节展示了类似的使用条件执行将字符转换为小写的示例。条件执行在级联条件方面更加强大。
示例6.18:
以下C代码用于判断c是否是元音字母:
if (c==‘a’ || c==‘e’ || c==‘i’ || c==‘o’ || c==‘u’)
{
vowel++;
}在汇编中,您可以使用条件比较来编写此代码:
TEQ c, #‘a’
TEQNE c, #‘e’
TEQNE c, #‘i’
TEQNE c, #‘o’
TEQNE c, #‘u’
ADDEQ vowel, vowel, #1一旦TEQ比较中的任何一个检测到匹配,cpsr中的Z标志就会被设置。接下来的TEQNE指令没有效果,因为它们是在Z = 0的条件下进行的。下一个有效的指令是ADDEQ,它会增加元音字母计数器。您可以在if语句中的所有比较都是相同类型时使用此方法。
示例6.19:
考虑以下代码,用于检测c是否为字母:
if ((c>=‘A’ && c<=‘Z’) || (c>=‘a’ && c<=‘z’))
{
letter++;
}要有效地实现此代码,我们可以使用加法或减法将每个范围移动到0 ≤ c ≤ limit的形式。然后,我们使用无符号比较来检测此范围,并使用条件比较来连接范围。以下汇编代码有效地实现了此操作:
SUB temp, c, #‘A’
CMP temp, #‘Z’-‘A’
SUBHI temp, c, #‘a’
CMPHI temp, #‘z’-‘a’
ADDLS letter, letter, #1
对于涉及开关的更复杂的决策,请参阅第6.8节。注意,逻辑操作AND和OR之间存在标准的逻辑关系,如表6.1所示。您可以通过反转涉及OR的逻辑表达式来得到涉及AND的表达式,这在简化或重新排列逻辑表达式时通常很有用。
总结条件执行:
- 您可以使用条件执行来实现大多数if语句。这比使用条件分支更高效。
- 您可以使用几个相似条件的逻辑AND或OR来实现if语句,使用的比较指令本身也是有条件的。
6.6 Looping Constructs
大多数对性能至关重要的例程将包含一个循环。在第5.3节中我们看到,在ARM架构中,循环在倒计时至零时速度最快。本节描述了如何在汇编中有效地实现这些循环。我们还会看一些将循环展开以获得最大性能的示例。
6.6.1 Decremented Counted Loops
//递减计数循环
对于一个递减循环,包含N个迭代,循环计数器i从N递减到1(包括1)。循环在i = 0时终止。一个高效的实现方式是:
MOV i, N
loop
; loop body goes here and i=N,N-1,...,1
SUBS i, i, #1
BGT loop循环开销由一次减法设置条件码和一次条件分支组成。在ARM7和ARM9上,每个循环的开销为四个时钟周期。如果i是一个数组索引,那么您可能希望从N-1递减到0(包括0),以便可以访问数组元素0。您可以使用不同的条件分支来实现这一点:
SUBS i, N, #1
loop
; loop body goes here and i=N-1,N-2,...,0
SUBS i, i, #1
BGE loop在这种排列中,Z标志位在循环的最后一次迭代中被设置,其他迭代中被清除。如果最后一次循环有任何不同之处,我们可以使用EQ和NE条件来实现这一点。例如,如果您为下一个循环预加载数据(如第6.3.1.1节所讨论的),那么您希望在最后一个循环中避免预加载。您可以将所有预加载操作都条件地执行NE,就像在第6.3.1.1节中一样。
没有必要在每个循环中递减一个。假设我们需要N/3次循环。与其试图将N除以三,更高效的做法是在每次迭代中从循环计数器中减去三:
MOV i, N
loop
; loop body goes here and iterates (round up)(N/3) times
SUBS i, i, #3
BGT loop6.6.2 Unrolled Counted Loops
//展开的计数循环
这将带我们进入循环展开的主题。循环展开通过多次执行循环体来减少循环开销。然而,还有一些问题需要解决。如果循环计数不是展开数量的倍数怎么办?如果循环计数小于展开数量怎么办?我们在第5.3节中研究了这些问题的C代码。在本节中,我们将看看如何在汇编中处理这些问题。
我们以C库函数memset作为案例研究。该函数将地址为s处的N个字节设置为字节值c。为了提高效率,我们将研究如何展开循环而不对输入操作数添加额外限制。我们的memset版本将具有以下C原型:
void my_memset(char *s, int c, unsigned int N);
为了在大的N上提高效率,我们需要使用STR或STM指令一次写入多个字节。因此,我们的首要任务是对齐数组指针s。然而,只有在N足够大的情况下才值得这样做。我们还不知道“足够大”是什么意思,但假设我们可以选择一个阈值T1,并且只在N≥T1时才对齐数组。显然,T1 ≥ 3,因为如果我们没有四个字节要写入,对齐就没有意义!
假设我们已经对齐了数组s。我们可以使用存储多个指令来高效地设置内存。例如,我们可以使用四个存储多个指令,每个指令存储八个字,以在每次循环中设置128个字节。但是,只有当N ≥ T2 ≥ 128时,这样做才值得,其中T2是稍后确定的另一个阈值。
最后,我们剩下要设置的N < T2个字节。我们可以使用STR以4个字节的块写入字节,直到N < 4。然后,我们可以使用STRB单独写入字节到数组末尾来完成。
例子6.20
这个例子展示了循环展开的memset例程。我们使用一行虚线将与前文段落对应的三个部分分隔开来。直到我们确定了T1和T2的最佳值之前,例程才算完成。
s RN 0 ; current string pointer
c RN 1 ; the character to fill with
N RN 2 ; the number of bytes to fill
c_1 RN 3 ; copies of c
c_2 RN 4
c_3 RN 5
c_4 RN 6
c_5 RN 7
c_6 RN 8
c_7 RN 12
; void my_memset(char *s, unsigned int c, unsigned int N)
my_memset
;-----------------------------------------------
; First section aligns the array
CMP N, #T_1 ; We know that T_1>=3
BCC memset_1ByteBlk ; if (N<T_1) goto memset_1ByteBlk
ANDS c_1, s, #3 ; find the byte alignment of s
BEQ aligned ; branch if already aligned
RSB c_1, c_1, #4 ; number of bytes until alignment
SUB N, N, c_1 ; number of bytes after alignment
CMP c_1, #2
STRB c, [s], #1
STRGEB c, [s], #1 ; if (c_1>=2) then output byte
STRGTB c, [s], #1 ; if (c_1>=3) then output byte
aligned
;the s array is now aligned
ORR c, c, c, LSL#8 ; duplicate the character
ORR c, c, c, LSL#16 ; to fill all four bytes of c
;-----------------------------------------------
; Second section writes blocks of 128 bytes
CMP N, #T_2 ; We know that T_2 >= 128
BCC memset_4ByteBlk ; if (N<T_2) goto memset_4ByteBlk
STMFD sp!, {c_2-c_6} ; stack scratch registers
MOV c_1, c
MOV c_2, c
MOV c_3, c
MOV c_4, c
MOV c_5, c
MOV c_6, c
MOV c_7, c
SUB N, N, #128 ; bytes left after next block
loop128 ; write 32 words = 128 bytes
STMIA s!, {c, c_1-c_6, c_7} ; write 8 words
STMIA s!, {c, c_1-c_6, c_7} ; write 8 words
STMIA s!, {c, c_1-c_6, c_7} ; write 8 words
STMIA s!, {c, c_1-c_6, c_7} ; write 8 words
SUBS N, N, #128 ; bytes left after next block
BGE loop128
ADD N, N, #128 ; number of bytes left
LDMFD sp!, {c_2-c_6} ; restore corrupted registers
;--------------------------------------------
; Third section deals with left over bytes
memset_4ByteBlk
SUBS N, N, #4 ; try doing 4 bytes
loop4 ; write 4 bytes
STRGE c, [s], #4
SUBGES N, N, #4
BGE loop4
ADD N, N, #4 ; number of bytes left
memset_1ByteBlk
SUBS N, N, #1
loop1 ; write 1 byte
STRGEB c, [s], #1
SUBGES N, N, #1
BGE loop1
MOV pc, lr ; finished so return我们需要找到阈值T1和T2的最佳值。为了确定这些值,我们需要分析不同范围N的循环计数。由于该算法操作的是大小为128字节、4字节和1字节的块,因此我们首先将N分解为这些块大小的组合:
N = 128Nh + 4Nm + Nl,其中0 ≤ Nm < 32,0 ≤ Nl < 4
现在我们将其分为三种情况。要了解这些循环计数的详细信息,您需要参考附录D中的指令周期计时数据。
■ 情况0 ≤ N < T1:在ARM9TDMI上,该例程需要5N + 6个周期(包括返回)。
■ 情况T1 ≤ N < T2:如果数组s是对齐的,第一个算法块需要6个周期;否则需要10个周期。假设每种对齐的可能性相等,平均为(6 + 10 + 10 + 10)/4 = 9个周期。第二个算法块需要6个周期。最后一个块需要5(32Nh + Nm) + 5(Nl + Zl) + 2个周期,其中Zl为1如果Nl = 0,否则为0。该情况下的总周期数为5(32Nh + Nm + Nl + Zl) + 17。
■ 情况N ≥ T2:与前一种情况类似,第一个算法块的平均周期数为9个。第二个算法块需要36Nh + 21个周期。最后一个算法块需要5(Nm + Zm + Nl + Zl) + 2个周期,其中Zm为1如果Nm为0,否则为0。该情况下的总周期数为36Nh + 5(Nm + Zm + Nl + Zl) + 32。

表6.2总结了这些结果。比较三行数据可以清楚地看到,只要Nm ≥ 1,并且Nm ≠ 1或者Nl ≠ 0,第二行的循环计数就优于第一行。我们将T1设置为5,选择第一行和第二行中最佳的循环计数。第三行只要Nh ≥ 1,就优于第二行。因此,我们将T2设置为128。
这个详细的例子向您展示了如何使用阈值来展开任何重要的循环,并在可能的输入值范围内提供良好的性能。
6.6.3 Multiple Nested Loops
在维护多个嵌套循环时,实际上只需要一个循环计数器,或更准确地说,只要每个循环计数所需的位数之和不超过32位。我们可以将这些循环计数合并到一个寄存器中,将最内层循环计数放置在最高位上。本节将通过示例展示如何做到这一点。我们将确保循环计数从最大值减1递减到0,以产生负结果来终止循环。
示例6.21展示了如何将三个循环计数合并为一个单一的循环计数。假设我们希望将矩阵B乘以矩阵C得到矩阵A,其中A、B、C具有以下常量维度。我们假设R、S、T相对较大,但小于256。
为了将这三个循环计数合并为一个单一的循环计数,我们可以在寄存器中为每个循环计数分配一定数量的位。在这种情况下,由于R、S、T小于256,我们可以给每个循环计数分配8位。
假设循环计数寄存器为L,最高位对应于最内层循环计数。为了初始化循环计数,我们将L的值设置为"R << 16 | S << 8 | T"。
在嵌套循环的执行过程中,我们每次迭代都将循环计数L减1,直到它达到0或变为负数为止。这样可以确保循环从其最大值减去1递减至0,循环通过产生负结果来终止。
通过将循环计数合并到一个单一的循环计数寄存器中,我们可以只使用一个循环计数器高效地维护和控制多个嵌套循环。
Matrix A:
R rows × T columns
Matrix B:
R rows × S columns
Matrix C:
S rows × T columns我们用相同名称的小写指针来表示每个矩阵,指向按行组织的字数组。例如,第i行第j列的元素A[i,j]在字节地址 &A[i,j]=a+ 4*(i*T+j)。
矩阵乘法的一个简单的C实现使用三个嵌套循环i、j和k:
#define R 40
#define S 40
#define T 40
void ref_matrix_mul(int *a, int *b, int *c)
{
unsigned int i,j,k;
int sum;
for (i=0; i<R; i++)
{
for (j=0; j<T; j++)
{
/* calculate a[i,j] */
sum = 0;
for (k=0; k<S; k++)
{
/* add b[i,k]*c[k,j] */
sum += b[i*S+k]*c[k*T+j];
}
a[i*T+j] = sum;
}
}
}这里有很多提高效率的方式,比如删除地址索引计算,但我们将集中精力于循环结构。我们分配一个寄存器计数器count,其中包含三个循环计数器i、j和k:

请注意,S - 1 - k 从 S - 1 递减到 0,而不是像 k 那样从 0 递增到 S - 1。下面的汇编代码使用寄存器 count 中的单个计数器来实现矩阵乘法:
R EQU 40
S EQU 40
T EQU 40
a RN 0 ; points to an R rows × T columns matrix
b RN 1 ; points to an R rows × S columns matrix
c RN 2 ; points to an S rows × T columns matrix
sum RN 3
bval RN 4
cval RN 12
count RN 14
matrix_mul ; void matrix_mul(int *a, int *b, int *c)
STMFD sp!, {r4, lr}
MOV count, #(R-1) ; i=0
loop_i
ADD count, count, #(T-1) << 8 ; j=0
loop_j
ADD count, count, #(S-1) << 16 ; k=0
MOV sum, #0
loop_k
LDR bval, [b], #4 ; bval = B[i,k], b=&B[i,k+1]
LDR cval, [c], #4*T ; cval = C[k,j], c=&C[k+1,j]
SUBS count, count, #1 << 16 ; k++
MLA sum, bval, cval, sum ; sum += bval*cval
BPL loop_k ; branch if k<=S-1
STR sum, [a], #4 ; A[i,j] = sum, a=&A[i,j+1]
SUB c, c, #4*S*T ; c = &C[0,j]
ADD c, c, #4 ; c = &C[0,j+1]
ADDS count, count, #(1 << 16)-(1 << 8) ; zero (S-1-k), j++
SUBPL b, b, #4*S ; b = &B[i,0]
BPL loop_j ; branch if j<=T-1
SUB c, c, #4*T ; c = &C[0,0]
ADDS count, count, #(1 >> 8)-1 ; zero (T-1-j), i++
BPL loop_i ; branch if i<=R-1
LDMFD sp!, {r4, pc}上述的结构比起朴素实现方式节省了两个寄存器。首先,我们递减位于16到23位的计数器,直到结果为负数为止。这实现了k循环,从S-1递减到0(包括0)。一旦结果为负数,代码会加上216来清除16到31位的值。然后我们减去28来递减位于8到15位的计数器,实现j循环。我们可以使用单个ARM指令高效地编码常量216 - 28 = 0xFF00。现在,8到15位的值从T-1递减到0。当加法和减法的结果为负数时,我们就完成了j循环。对于i循环,我们重复相同的过程。ARM可以处理加法和减法指令中的广泛范围的旋转常量,使得这种方案非常高效。
//可以试下C语言和汇编的例子,写成testbed,测试下perf
6.6.4 Other Counted Loops
您可能希望在循环中将循环计数器的值作为计算的输入。并不总是希望从N递减到1或从N-1递减到0。例如,您可能希望逐个从数据寄存器中选择位,这种情况下您可能需要一个每次迭代都加倍的二次幂掩码。
以下子节展示了以不同模式计数的有用循环结构。它们使用只有一条指令与一个分支相结合来实现循环。
6.6.4.1 Negative Indexing
这个循环结构以步长为 STEP,从-N递减到0(包括或不包括0)计数。
RSB i, N, #0 ; i=-N
loop
; loop body goes here and i=-N,-N+STEP,...,
ADDS i, i, #STEP
BLT loop
; use BLT or BLE to exclude 0 or not6.6.4.2 Logarithmic Indexing
这个循环结构以2的幂次从2N递减到1进行计数。例如,如果 N = 4,则计数为 16、8、4、2、1。
MOV i, #1
MOV i, i, LSL N
loop
; loop body
MOVS i, i, LSR#1
BNE loop下面的循环结构从N位掩码递减到1位掩码。例如,如果N = 4,则计数为15、7、3、1。
MOV i, #1
RSB i, i, i, LSL N ; i=(1 << N)-1
loop
; loop body
MOVS i, i, LSR#1
BNE loop循环结构总结:
- ARM需要两条指令来实现计数循环:一个减法指令用于设置标志位,一个条件分支指令。
- 对循环进行展开可以提高循环性能,但不要过度展开,因为这会影响缓存的性能。对于迭代次数较小的循环展开可能效率低下,可以通过测试迭代次数来决定是否调用展开后的循环。
- 嵌套循环只需要一个循环计数器寄存器,这可以提高效率,为其他用途释放出寄存器。
- ARM可以高效地实现负索引和对数索引的循环。
6.7 Bit Manipulation
压缩文件格式以位为粒度打包项目,以最大化数据密度。这些项目可以是固定宽度的,例如长度字段或版本字段,也可以是可变宽度的,例如Huffman编码的符号。在压缩中,Huffman编码用于为每个符号分配一串位的编码。对于常见的符号,编码较短,对于罕见的符号,编码较长。
在本节中,我们将介绍处理位流的有效方法。首先,我们将讨论固定宽度编码,然后是可变宽度编码。有关常见的位操作例程(如字节序和位反转),请参阅第7.6节。
6.7.1 Fixed-Width Bit-Field Packing and Unpacking
//固定宽度的位字段打包和解包
在ARM寄存器中提取无符号位字段,如果预先设置掩码,可以在一个周期内完成;否则需要两个周期。对于有符号位字段,除非位字段位于字(最高有效位是寄存器的最高有效位),否则始终需要两个周期来解包。在ARM中,我们使用逻辑操作和移位器来进行编码的打包和解包,如下面的示例所示。
示例6.22
汇编代码展示了如何从寄存器r0中解包位4到15,并将结果放入r1中。
; unsigned unpack with mask set up in advance
; mask=0x00000FFF
AND r1, mask, r0, LSR#4
; unsigned unpack with no mask
MOV r1, r0, LSL#16 ; discard bits 16-31
MOV r1, r1, LSR#20 ; discard bits 0-3 and zero extend
; signed unpack
MOV r1, r0, LSL#16 ; discard bits 16-31
MOV r1, r1, ASR#20 ; discard bits 0-3 and sign extend示例: 6.23 如果r1已经限制在正确的范围,并且r0的相应位字段为空,则将值r1打包到位压缩寄存器r0中只需要一个周期。在这个示例中,r1是一个12位的数字,要插入到r0的第4位。
; pack r1 into r0
ORR r0, r0, r1, LSL #4否则,您需要设置一个掩码寄存器:
; pack r1 into r0
; mask=0x00000FFF set up in advance
AND r1, r1, mask ; restrict the r1 range
BIC r0, r0, mask, LSL#4 ; clear the destination bits
ORR r0, r0, r1, LSL#4 ; pack in the new data6.7.2 Variable-Width Bitstream Packing
我们的任务是将一系列可变长度的编码打包成一个位流。通常,我们会对数据流进行压缩,而可变长度的编码表示哈夫曼或算术编码符号。然而,为了有效地进行打包,我们不需要做出任何关于编码表示的假设。

我们需要注意位打包的字节序。许多压缩文件格式使用大端字节序的位打包顺序,其中第一个编码位于第一个字节的最高有效位。因此,我们将在示例中使用大端字节序的位打包顺序。这有时被称为网络字节序。图6.5展示了如何使用大端打包顺序将可变长度的位码形成字节流。"High"和"low"分别表示字节的最高有效位和最低有效位。
为了在ARM上高效实现打包,我们使用一个32位寄存器作为缓冲区,按照大端序存储四个字节。换句话说,我们将字节流的第0个字节放置在寄存器的最高8位。然后,我们可以逐个将编码插入寄存器中,从最高有效位开始,逐位往下,直到最低有效位。一旦寄存器被填满,我们就可以将32位存储到内存中。对于大端存储系统,我们可以直接存储这个字;对于小端存储系统,我们需要在存储之前反转字节顺序。

我们将插入代码的32位寄存器称为bitbuffer。我们需要一个名为bitsfree的第二个寄存器来记录bitbuffer中尚未使用的位数。换句话说,bitbuffer包含32 - bitsfree个代码位和bitsfree个零位,如图6.6所示。要将k位的代码插入bitbuffer,我们从bitsfree中减去k,然后使用bitsfree的左移插入代码。
我们还需要注意对齐。字节流不一定是字对齐的,因此我们不能使用字访问来写入它。为了允许字访问,我们将首先备份到最后一个字对齐的地址。然后,我们用备份的数据填充32位寄存器bitbuffer。从那时起,我们可以使用字(32位)的读写操作。
例子6.24
该示例提供了三个函数:bitstream_write_start、bitstream_write_code和bitstream_write_flush。这些函数不符合ATPCS规范,因为它们假设像bitbuffer这样的寄存器在调用之间被保留。在实践中,您可以内联此代码以提高效率,所以这不是一个问题。
bitstream_write_start函数对齐位流指针bitstream并初始化32位缓冲区bitbuffer。每次调用bitstream_write_code函数,都会将长度为codebits的值code插入其中。最后,bitstream_write_flush函数将任何剩余的字节写入位流,以终止流。
bitstream RN 0 ; current byte address in the output bitstream
code RN 4 ; current code
codebits RN 5 ; length in bits of current code
bitbuffer RN 6 ; 32-bit output big-endian bitbuffer
bitsfree RN 7 ; number of bits free in the bitbuffer
tmp
RN 8 ; scratch register
mask RN 12 ; endian reversal mask 0xFFFF00FF
bitstream_write_start
MOV bitbuffer, #0
MOV bitsfree, #32
align_loop
TST bitstream, #3
LDRNEB code, [bitstream, #-1]!
SUBNE bitsfree, bitsfree, #8
ORRNE bitbuffer, code, bitbuffer, ROR #8
BNE align_loop
MOV bitbuffer, bitbuffer, ROR #8
MOV pc, lr
bitstream_write_code
SUBS bitsfree, bitsfree, codebits
BLE full_buffer
ORR bitbuffer, bitbuffer, code, LSL bitsfree
MOV pc, lr
full_buffer
RSB bitsfree, bitsfree, #0
ORR bitbuffer, bitbuffer, code, LSR bitsfree
IF {ENDIAN}="little"
; byte reverse the bit buffer prior to storing
EOR tmp, bitbuffer, bitbuffer, ROR #16
AND tmp, mask, tmp, LSR #8
EOR bitbuffer, tmp, bitbuffer, ROR #8
ENDIF
STR bitbuffer, [bitstream], #4
RSB bitsfree, bitsfree, #32
MOV bitbuffer, code, LSL bitsfree
MOV pc, lr
bitstream_write_flush
RSBS bitsfree, bitsfree, #32
flush_loop
MOVGT bitbuffer, bitbuffer, ROR #24
STRGTB bitbuffer, [bitstream], #1
SUBGTS bitsfree, bitsfree, #8
BGT flush_loop
MOV pc, lr6.7.3 Variable-Width Bitstream Unpacking
解压可变宽度代码的位流比打包要困难得多。问题在于,我们通常不知道正在解压的代码的宽度!对于Huffman编码的位流,您必须通过查看下一个比特序列并确定它是哪个代码来推导出每个代码的长度。
在这里,我们将使用查找表来加速解压过程。想法是获取位流的下一个N位,并在两个大小为2N条目的查找表look_codebits[]和look_code[]中进行查找。如果下一个N位足以确定代码,则这些表分别告诉我们代码长度和代码值。如果下一个N位不足以确定代码,则look_codebits表将返回一个逃逸值0xFF。逃逸值只是一个标志,表示这种情况是异常情况。
在Huffman代码序列中,常见代码长度较短,而稀有代码长度较长。因此,我们希望能够快速解码大多数常见代码,使用查找表。在下面的例子中,我们假设N = 8,并使用256个条目的查找表。
例子6.25
该示例提供了三个函数,用于解压存储在字节流中的大端位流。与例6.24类似,这些函数不符合ATPCS规范,并且通常会被内联。函数bitstream_read_start初始化该过程,在位流的字节地址bitstream上开始解码。每次调用bitstream_read_code函数都会将下一个代码返回给寄存器code。该函数仅处理可以从查找表中读取的短代码。长代码会陷入到标签long_code,但是此函数的实现取决于您正在解码的代码。

代码使用一个寄存器bitbuffer,其中包含从最高有效位开始的N + bitsleft个代码位(参见图6.7)。
bitstream RN 0 ; current byte address in the input bitstream
look_code RN 2 ; lookup table to convert next N bits to a code
look_codebits RN 3 ; lookup table to convert next N bits to a code length
code RN 4 ; code read
codebits RN 5 ; length of code read
bitbuffer RN 6 ; 32-bit input buffer (big endian)
bitsleft RN 7 ; number of valid bits in the buffer - N
tmp
RN 8 ; scratch
tmp2 RN 9 ; scratch
mask RN 12 ; N-bit extraction mask (1 << N)-1
N
EQU 8 ; use a lookup table on 8 bits (N must be <= 9)
bitstream_read_start
MOV bitsleft, #32
read_fill_loop
LDRB tmp, [bitstream], #1
ORR bitbuffer, tmp, bitbuffer, LSL#8
SUBS bitsleft, bitsleft, #8
BGT read_fill_loop
MOV bitsleft, #(32-N)
MOV mask, #(1 << N)-1
MOV pc, lr
bitstream_read_code
LDRB codebits, [look_codebits, bitbuffer, LSR# (32-N)]
AND code, mask, bitbuffer, LSR#(32-N)
LDR code, [look_code, code, LSL#2]
SUBS bitsleft, bitsleft, codebits
BMI empty_buffer_or_long_code
MOV bitbuffer, bitbuffer, LSL codebits
MOV pc, lr
empty_buffer_or_long_code
TEQ codebits, #0xFF
BEQ long_code
; empty buffer - fill up with 3 bytes
; as N <= 9, we can fill 3 bytes without overflow
LDRB tmp, [bitstream], #1
LDRB tmp2, [bitstream], #1
MOV bitbuffer, bitbuffer, LSL codebits
LDRB codebits, [bitstream], #1
ORR tmp, tmp2, tmp, LSL#8
RSB bitsleft, bitsleft, #(8-N)
ORR tmp, codebits, tmp, LSL#8
ORR bitbuffer, bitbuffer, tmp, LSL bitsleft
RSB bitsleft, bitsleft, #(32-N)
MOV pc, lr
long_code
; handle the long code case depending on the application
; here we just return a code of -1
MOV code, #-1
MOV pc, lr计数器bitsleft实际上计算的是缓冲区bitbuffer中剩余的位数减去下一个查找所需的N位。因此,只要bitsleft ≥ 0,我们就可以执行下一个表查找。一旦bitsleft < 0,就有两种可能性。一种可能性是我们找到了一个有效的代码,但没有足够的位数来查找下一个代码。另一种可能性是codebits包含了逃逸值0xFF,表示代码长度超过了N位。我们可以使用调用empty_buffer_or_long_code一次捕获这两种情况。如果缓冲区为空,我们将其填充为24位。如果我们检测到了一个长代码,我们将跳转到long_code陷阱。
在ARM9TDMI上,该示例在最佳情况下每个代码解压缩需要七个周期。如果提前知道打包的位字段的大小,可以获得更快的结果。
总结:位操作
■ 使用逻辑操作和移位寄存器,ARM可以高效地对位进行打包和解压缩。
■ 要高效访问位流,请使用一个32位寄存器作为位缓冲区。使用第二个寄存器跟踪位缓冲区中有效位的数量。
■ 要高效解码位流,请使用查找表扫描位流的下一个N位。查找表可以直接返回最多N位长的代码,或者对于更长的代码返回一个逃逸字符。
6.8 Efficient Switches
一个开关或多路分支可以在多个不同的动作之间进行选择。在本节中,我们假设动作取决于变量x。对于不同的x值,我们需要执行不同的动作。本节将讨论如何使用汇编语言高效地实现针对不同类型的x的开关。
6.8.1 Switches on the Range 0 ≤ x<N
示例C函数`ref_switch`根据x的值执行不同的操作。我们只对范围在0 ≤ x < 8的x值感兴趣。
int ref_switch(int x)
{
switch (x)
{
case 0: return method_0();
case 1: return method_1();
case 2: return method_2();
case 3: return method_3();
case 4: return method_4();
case 5: return method_5();
case 6: return method_6();
case 7: return method_7();
default: return method_d();
}
}有两种方法可以在ARM汇编中高效地实现这个结构。第一种方法使用一个函数地址表。我们通过从由x索引的表中加载pc来实现。
示例6.26
`switch_absolute`代码使用一个内联的函数指针表执行开关操作:
x RN 0
; int switch_absolute(int x)
switch_absolute
CMP x, #8
LDRLT pc, [pc, x, LSL#2]
B method_d
DCD method_0
DCD method_1
DCD method_2
DCD method_3
DCD method_4
DCD method_5
DCD method_6
DCD method_7这段代码有效的原因是pc寄存器是流水线化的。当ARM执行LDR指令时,pc指向method_0单词。
上述方法非常快速,但有一个缺点:代码不具备位置无关性,因为它在内存中存储了方法函数的绝对地址。位置无关代码通常用于在运行时将模块安装到系统中。下面的示例展示了如何解决这个问题。
示例 6.27 与switch_absolute相比,switch_relative代码稍慢一些,但它是位置无关的:
; int switch_relative(int x)
switch_relative
CMP x, #8
ADDLT pc, pc, x, LSL#2
B method_d
B method_0
B method_1
B method_2
B method_3
B method_4
B method_5
B method_6
B method_7还有一个最后的优化可以实施。如果方法函数很短,你可以将指令内联到分支指令的位置。
例如 6.28 假设每个非默认方法都有一个包含四条指令的实现。那么你可以使用以下形式的代码:
CMP x, #8
ADDLT pc, pc, x, LSL#4 ; each method is 16 bytes long
B method_d
method_0
; the four instructions for method_0 go here
method_1
; the four instructions for method_1 go here
; ... continue in this way ...6.8.2 Switches on a General Value x
现在假设x不在方便的范围0≤x<N内,其中N足够小以应用6.8.1节中的方法。在不需要逐个测试x与每个可能的值相比较的情况下,我们如何高效地执行switch操作呢?
在这种情况下,一种非常有用的技术是使用散列函数(哈希函数)。散列函数是任何将我们感兴趣的值映射到形式为0≤y<N的连续范围的函数y = f (x)。我们可以使用y = f (x)来代替对x进行switch操作。如果出现碰撞,即两个x值映射到相同的y值,则可以处理碰撞。在这种情况下,我们需要进一步的代码来测试所有可能导致该y值的x值。对于我们的目的来说,一个好的散列函数应该容易计算并且不会产生太多的碰撞。
为了执行switch操作,我们先应用散列函数,然后在散列值y上使用6.8.1节中优化过的switch代码。当两个x值可以映射到相同的散列值时,我们需要进行显式测试,但对于一个好的散列函数来说,这种情况应该很少发生。
6.29示例中,假设我们想要在x = 2^k的情况下调用method_k,其中x的取值范围是1, 2, 4, 8, 16, 32, 64, 128。对于x的所有其他值,我们需要调用默认方法method_d。我们需要找到一个由乘以2的幂减1形成的散列函数(这在ARM上是一种高效的操作)。通过尝试不同的乘数,我们发现15 × 31 × y在第9至第11位(最右边第0位)上的值对应于八个情况下的不同值。这意味着我们可以将这个乘积的第9至第11位作为我们的散列函数。
y=1, 15x31x1=000111010001 , k=0
y=2, 15x31x2=001110100010 , k=1
y=3, 15x31x3=010101110011 , k=2
y=4, 15x31x4=011101000100 , k=3
y=5, 15x31x5=100100010101 , k=4
y=6, 15x31x6=101011100110 , k=5
y=7, 15x31x7=110010110111 , k=6
y=8, 15x31x8=111010001000 , k=7
以下是使用该散列函数执行switch操作的汇编代码switch_hash。请注意,其他不是2的幂的值会与我们要检测的值具有相同的散列值。switch操作将情况缩小到单个2的幂,我们可以显式测试。如果x不是2的幂,则会执行默认情况,调用method_d。
x RN 0
hash RN 1
; int switch_hash(int x)
switch_hash
RSB hash, x, x, LSL#4 ; hash=x*15
RSB hash, hash, hash, LSL#5 ; hash=x*15*31
AND hash, hash, #7 << 9 ; mask out the hash value
ADD pc, pc, hash, LSR#6
NOP
TEQ x, #0x01
BEQ method_0
TEQ x, #0x02
BEQ method_1
TEQ x, #0x40
BEQ method_6
TEQ x, #0x04
BEQ method_2
TEQ x, #0x80
BEQ method_7
TEQ x, #0x20
BEQ method_5
TEQ x, #0x10
BEQ method_4
TEQ x, #0x08
BEQ method_3
B method_d高效的switch语句总结如下:
■ 确保switch值在某个小范围内,即0 ≤ x < N,其中N为一个较小的数值。为了实现这一点,你可能需要使用散列函数进行转换。
■ 使用switch值作为索引来查找函数指针表,或者根据switch值在代码中的位置定期分支到短代码段。第二种技术是位置无关的,而第一种技术则不是。
请注意,上述两种技术都可以实现高效的switch语句。使用函数指针表提供了更加优雅和灵活的解决方案,而将代码分成块的方法则更适用于特定场景。选择哪种技术取决于应用的具体需求和限制条件。
6.9 Handling Unaligned Data
在ARM架构中,如果加载或存储使用的地址不是数据传输宽度的倍数,则称为非对齐访问。为了确保代码在不同的ARM架构和实现中具有可移植性,必须避免进行非对齐访问。第5.9节介绍了C语言中处理非对齐访问的方法。在本节中,我们将介绍如何在汇编代码中处理非对齐访问。
最简单的方法是使用字节加载和存储来逐个字节地访问数据。这是推荐的方法,适用于对速度要求不高的访问。以下示例展示了如何以这种方式访问字值。
示例6.30:
该示例展示了如何使用非对齐地址p读取或写入一个32位字。我们使用三个临时寄存器t0、t1和t2来避免冲突。在ARM9TDMI上,所有非对齐字操作需要七个周期。请注意,我们需要针对大端或小端格式存储的32位字分别使用不同的函数。
p RN 0
x RN 1
t0 RN 2
t1 RN 3
t2 RN 12
; int load_32_little(char *p)
load_32_little
LDRB x, [p]
LDRB t0, [p, #1]
LDRB t1, [p, #2]
LDRB t2, [p, #3]
ORR x, x, t0, LSL#8
ORR x, x, t1, LSL#16
ORR r0, x, t2, LSL#24
MOV pc, lr
; int load_32_big(char *p)
load_32_big
LDRB x, [p]
LDRB t0, [p, #1]
LDRB t1, [p, #2]
LDRB t2, [p, #3]
ORR x, t0, x, LSL#8
ORR x, t1, x, LSL#8
ORR r0, t2, x, LSL#8
MOV pc, lr
; void store_32_little(char *p, int x)
store_32_little
STRB x, [p]
MOV t0, x, LSR#8
STRB t0, [p, #1]
MOV t0, x, LSR#16
STRB t0, [p, #2]
MOV t0, x, LSR#24
STRB t0, [p, #3]
MOV pc, lr
; void store_32_big(char *p, int x)
store_32_big
MOV t0, x, LSR#24
STRB t0, [p]
MOV t0, x, LSR#16
STRB t0, [p, #1]
MOV t0, x, LSR#8
STRB t0, [p, #2]
STRB x, [p, #3]
MOV pc, lr如果您需要比每次访问七个周期更好的性能,那么您可以编写几个不同的变体函数,每个变体函数处理不同的地址对齐方式。这将将非对齐访问的开销降低为三个周期:字加载和两个算术指令来将值组合在一起。
示例6.31:
该示例展示了如何从可能是非对齐地址data开始生成N个字的校验和。该代码适用于小端内存系统。请注意,我们可以使用汇编器的宏指令来生成四个函数checksum_0、checksum_1、checksum_2和checksum_3。函数checksum_a处理data是形式为4 + a的地址的情况。
使用宏指令可以节省编程工作量。我们只需要编写一个宏指令,并将其实例化四次以实现我们的四个校验和函数。
sum RN 0 ; current checksum
N RN 1 ; number of words left to sum
data RN 2 ; word aligned input data pointer
w RN 3 ; data word
; int checksum_32_little(char *data, unsigned int N)
checksum_32_little
BIC data, r0, #3 ; aligned data pointer
AND w, r0, #3 ; byte alignment offset
MOV sum, #0
; initial checksum
LDR pc, [pc, w, LSL#2] ; switch on alignment
NOP
; padding
DCD checksum_0
DCD checksum_1
DCD checksum_2
DCD checksum_3
MACRO
CHECKSUM $alignment
checksum_$alignment
LDR w, [data], #4 ; preload first value
10 ; loop
IF $alignment<>0
ADD sum, sum, w, LSR#8*$alignment
LDR w, [data], #4
SUBS N, N, #1
ADD sum, sum, w, LSL#32-8*$alignment
ELSE
ADD sum, sum, w
LDR w, [data], #4
SUBS N, N, #1
ENDIF
BGT %BT10
MOV pc, lr
MEND
; generate four checksum routines
; one for each possible byte alignment
CHECKSUM 0
CHECKSUM 1
CHECKSUM 2
CHECKSUM 3您现在可以像第6.6.2节中所示,展开和优化这些函数以实现最快的速度。由于代码大小的增加,只有在对时间要求非常高的函数中才使用前面的技术。
处理非对齐数据的总结:
- 如果性能不是问题,可以使用多个字节加载和存储来访问非对齐数据。这种方法可以访问给定字节序的数据,而不考虑指针对齐和内存系统配置的字节序。
- 如果性能是一个问题,那么可以使用多个函数,每个函数针对可能的数组对齐方式进行优化。您可以使用汇编器的宏指令来自动生成这些函数。
6.10 Summary
为了实现最佳性能,您需要编写优化的汇编程序。只有对性能影响较大的关键函数进行优化才是值得的。您可以使用性能分析或周期计数工具(例如ARM的ARMulator模拟器)来找到这些关键函数。
本章介绍了针对ARM汇编优化的示例和实用技巧,以下是关键思想:
- 安排代码,以避免处理器的互锁和停顿。使用附录D查看指令结果可用的时间。特别注意加载和乘法指令,因为它们通常需要很长时间才能产生结果。
- 尽量使用14个可用的通用寄存器保存数据。有时可以将多个数据项打包到一个寄存器中。避免在内层循环中进行数据堆栈操作。
- 对于小的条件语句,使用条件数据处理操作而不是条件分支。
- 使用倒计数的展开循环以实现最大的循环性能。
- 对于位压缩数据的打包和解包,使用32位寄存器缓冲区以提高效率并减少内存数据带宽。
- 使用分支表和哈希函数来实现高效的switch语句。
- 要高效处理非对齐数据,请使用多个函数。为输入和输出数组的特定对齐方式优化每个函数。在运行时根据情况选择函数。
Chapter7 Optimized Primitives
原语是一种基本操作,可以在各种不同的算法和程序中使用。例如,加法、乘法、除法和随机数生成都是原语。一些原语直接由ARM指令集支持,包括32位加法和乘法。然而,许多原语在指令中没有直接支持,我们必须编写程序来实现它们(例如,除法和随机数生成)。
本章提供了常见原语的优化参考实现。前三个部分介绍了乘法和除法。第7.1节介绍了实现扩展精度乘法的原语。第7.2节介绍了规范化,这对于第7.3节中的除法算法非常有用。
接下来的两节介绍了更复杂的数学运算。第7.4节讨论了平方根。第7.5节介绍了对数、指数、正弦和余弦等超越函数。第7.6节介绍了涉及位操作的运算,第7.7节介绍了饱和和舍入等运算。最后,第7.8节介绍了随机数生成。
您可以以两种方式使用本章内容。首先,它可以作为一个直接的参考。如果您需要一个除法程序,请查找索引并找到该程序所在的部分,或者找到关于除法的部分。您可以从书籍网站上复制汇编代码。其次,本章提供了理论解释每个实现原理的知识,这对于需要更改或泛化程序的情况非常有用。例如,您可能对输入和输出操作数的精度或格式有不同的要求。因此,本文中包含许多数学公式和一些繁琐的证明。您可以根据需要选择是否跳过这些内容!
我们设计了代码示例,使其成为可以直接从网站上获取的完整函数。它们应该可以立即使用ARM提供的工具包进行汇编。为了一致性,我们在本章的所有示例中都使用ARM工具包ADS1.1。有关汇编器格式的帮助,请参阅附录中的第A.4节。您也可以使用GNU汇编器gas。有关gas汇编器格式的帮助,请参阅第A.5节。
您还会注意到,我们使用C关键字__value_in_regs。在ARM编译器armcc中,这表示函数参数或返回值应通过寄存器传递,而不是通过引用传递。在实际应用中,这不是一个问题,因为您将内联操作以提高效率。
在本章中,我们使用符号Qk表示二进制小数点位于第k-1位和第k位之间的定点表示法。例如,在Q15中表示的0.75是整数值0x6000。有关Qk表示法和定点算术的更多详细信息,请参阅第8.1节。我们说"d < 0.5 at Q15"表示d表示值d2−15,并且此值小于一半。
7.1 Double-Precision Integer Multiplication
您可以使用UMULL和SMULL指令将整数扩展到32位宽度。以下例程可以对64位有符号或无符号整数进行乘法运算,并得到64位或128位的结果。使用相同的思路,它们可以扩展到乘法运算中的任意长度的整数。更长的乘法运算对于处理long long C类型、模拟双精度固定点或浮点运算,以及公钥密码学中所需的长算术非常有用。

我们使用小端记法表示多字节值。如果一个128位整数存储在四个寄存器a3、a2、a1、a0中,那么它们分别存储的是[127:96]、[95:64]、[63:32]、[31:0]位(参见图7.1)。
7.1.1 long long Multiplication
使用以下三个指令序列将两个64位值(有符号或无符号)b和c相乘,得到一个新的64位long long值a。不包括ARM Thumb过程调用标准(ATPCS)包装器,并且在最坏情况下的输入时,此操作在ARM7TDMI上需要24个周期,在ARM9TDMI上需要25个周期。在ARM9E上,该操作需要8个周期。其中一个周期是第一个UMULL和MLA之间的流水线互锁,您可以通过与其他代码交替执行来消除它。
b_0 RN 0 ; b bits [31:00] (b low)
b_1 RN 1 ; b bits [63:32] (b high)
c_0 RN 2 ; c bits [31:00] (c low)
c_1 RN 3 ; c bits [63:32] (c high)
a_0 RN 4 ; a bits [31:00] (a low-low)
a_1 RN 5 ; a bits [63:32] (a low-high)
a_2 RN 12 ; a bits [95:64] (a high-low)
a_3 RN lr ; a bits [127:96] (a high-high)
; long long mul_64to64 (long long b, long long c)
mul_64to64
STMFD sp!, {r4,r5,lr}
; 64-bit a = 64-bit b * 64-bit c
UMULL a_0, a_1, b_0, c_0
; low*low
MLA a_1, b_0, c_1, a_1
; low*high
MLA a_1, b_1, c_0, a_1
; high*low
; return wrapper
MOV r0, a_0
MOV r1, a_1
LDMFD sp!, {r4,r5,pc}7.1.2 Unsigned 64-Bit by 64-Bit Multiply with 128-Bit Result
对于具有128位结果的无符号64位乘法运算,有两种略有不同的实现方法。第一种在ARM7M上速度更快。在这种情况下,相比于非累加版本,乘积累加指令需要额外的一个周期。ARM7M版本需要四次长乘法和六次加法,最坏情况下需要30个周期来完成。
; __value_in_regs struct { unsigned a0,a1,a2,a3; }
; umul_64to128_arm7m(unsigned long long b,
;
unsigned long long c)
umul_64to128_arm7m
STMFD sp!, {r4,r5,lr}
; unsigned 128-bit a = 64-bit b * 64-bit c
UMULL a_0, a_1, b_0, c_0 ; low*low
UMULL a_2, a_3, b_0, c_1 ; low*high
UMULL c_1, b_0, b_1, c_1 ; high*high
ADDS a_1, a_1, a_2
ADCS a_2, a_3, c_1
ADC a_3, b_0, #0
UMULL c_0, b_0, b_1, c_0 ; high*low
ADDS a_1, a_1, c_0
ADCS a_2, a_2, b_0
ADC a_3, a_3, #0
; return wrapper
MOV r0, a_0
MOV r1, a_1
MOV r2, a_2
MOV r3, a_3
LDMFD sp!, {r4,r5,pc}第二种方法在ARM9TDMI和ARM9E上效果更好。在这种情况下,乘积累加与乘法的速度相同。我们对乘法指令进行调度,以避免在ARM9E上发生结果使用互锁(有关流水线和互锁的说明,请参见第6.2节)。
; __value_in_regs struct { unsigned a0,a1,a2,a3; }
; umul_64to128_arm9e(unsigned long long b,
;
unsigned long long c)
umul_64to128_arm9e
STMFD sp!, {r4,r5,lr}
; unsigned 128-bit a = 64-bit b * 64-bit c
UMULL a_0, a_1, b_0, c_0 ; low*low
MOV a_2, #0
UMLAL a_1, a_2, b_0, c_1 ; low*high
MOV a_3, #0
UMLAL a_1, a_3, b_1, c_0 ; high*low
MOV b_0, #0
ADDS a_2, a_2, a_3
ADC a_3, b_0, #0
UMLAL a_2, a_3, b_1, c_1 ; high*high
; return wrapper
MOV r0, a_0
MOV r1, a_1
MOV r2, a_2
MOV r3, a_3
LDMFD sp!, {r4,r5,pc}在排除函数调用和返回包装的情况下,该实现在ARM9TDMI上需要33个周期,在ARM9E上需要17个周期。这个想法是,如果a、b、c和d都是无符号32位整数,那么操作ab + c + d不会导致无符号64位整数溢出。因此,您可以使用常规的竖式乘法方法来实现长乘法,其中使用了ab + c + d操作,其中c和d是水平和垂直进位。
7.1.3 Signed 64-Bit by 64-Bit Multiply with 128-Bit Result
一个有符号的64位整数可以分解为有符号的高32位和无符号的低32位。要将b的高位与c的低位相乘,需要一条有符号乘以无符号的乘法指令。尽管ARM没有这样的指令,但我们可以使用宏合成一个。
以下是宏定义USMLAL提供了一种无符号乘以有符号的累加操作。为了将无符号的b与有符号的c相乘,它首先将这两个值都视为有符号数计算乘积bc。如果b的最高位设置为1,那么这个有符号数乘积还要乘以2^32-b。在这种情况下,它通过加上c*2^32来纠正结果。类似地,SUMLAL执行有符号乘以无符号的累加运算。
MACRO
USMLAL $al, $ah, $b, $c
; signed $ah.$al += unsigned $b * signed $c
SMLAL $al, $ah, $b, $c ; a = (signed)b * c;
TST $b, #1 << 31
; if ((signed)b<0)
ADDNE $ah, $ah, $c
; a += (c << 32);
MEND
MACRO
SUMLAL $al, $ah, $b, $c
; signed $ah.$al += signed $b * unsigned $c
SMLAL $al, $ah, $b, $c
;a=b* (signed)c;
TST $c, #1 << 31
; if ((signed)c<0)
ADDNE $ah, $ah, $b
; a += (b << 32);
MEND使用这些宏,将第7.1.2节中的64位乘法转换为有符号乘法相对简单。由于有符号与无符号修复指令,这个有符号版本比对应的无符号版本多了四个周期。
; __value_in_regs struct { unsigned a0,a1,a2; signed a3; }
; smul_64to128(long long b, long long c)
smul_64to128
STMFD sp!, {r4,r5,lr}
; signed 128-bit a = 64-bit b * 64-bit c
UMULL a_0, a_1, b_0, c_0 ; low*low
MOV a_2, #0
USMLAL a_1, a_2, b_0, c_1 ; low*high
MOV a_3, #0
SUMLAL a_1, a_3, b_1, c_0 ; high*low
MOV b_0, a_2, ASR#31
ADDS a_2, a_2, a_3
ADC a_3, b_0, a_3, ASR#31
SMLAL a_2, a_3, b_1, c_1 ; high*high
; return wrapper
MOV r0, a_0
MOV r1, a_1
MOV r2, a_2
MOV r3, a_3
LDMFD sp!, {r4,r5,pc}7.2 Integer Normalization and Count Leading Zeros
当整数的最高位(或者最重要的位)处于已知的位位置时,这个整数就被称为归一化。我们需要归一化来实现牛顿-拉弗森除法(参见第7.3.2节)或者转换为浮点数格式。在计算对数(参见第7.5.1节)和某些调度例程中使用的优先级解码器时,归一化也非常有用。在这些应用中,我们需要知道归一化值和达到该值所需的移位量。
这个操作非常重要,从ARM架构ARMv5E开始提供了指令来加速归一化过程。CLZ指令用于计算第一个有效位之前的前导零数。如果根本不存在有效的1位,则返回32。CLZ的值就是您需要应用的左移量,用于将整数归一化,使得最高位位于第31位。
7.2.1 Normalization on ARMv5 and Above
在ARMv5架构上,可以使用以下代码分别执行无符号和有符号归一化。无符号归一化左移,直到最高位位于第31位。有符号归一化左移,直到第31位有一个符号位,并且最高位位于第30位。两个函数都返回一个由两个值组成的结构体,即归一化的整数和进行归一化所需的左移。
x RN 0 ; input, output integer
shift RN 1 ; shift to normalize
; __value_in_regs struct { unsigned x; int shift; }
; unorm_arm9e(unsigned x)
unorm_arm9e
CLZ shift, x
; left shift to normalize
MOV x, x, LSL shift ; normalize
MOV pc, lr
; __value_in_regs struct { signed x; int shift; }
; unorm_arm9e(signed x)
snorm_arm9e
; [ s s s 1-s x x ... ]
EOR shift, x, x, LSL#1
; [ 0 0 1 x x x ... ]
CLZ shift, shift ; left shift to normalize
MOV x, x, LSL shift ; normalize
MOV pc, lr请注意,我们通过使用逻辑异或将有符号归一化转换为无符号归一化。如果x是有符号数,则x∧(x∧1)的最高位位于x的第一个符号位的位置上。
7.2.2 Normalization on ARMv4
如果您正在使用ARM7TDMI或ARM9TDMI等ARMv4架构处理器,则没有可用的CLZ指令。但是,我们可以合成相同的功能。unorm_arm7m中的简单分治方法在性能和代码大小之间取得了良好的平衡。我们依次测试是否可以将x左移16、8、4、2和1位。
; __value_in_regs struct { unsigned x; int shift; }
; unorm_arm7m(unsigned x)
unorm_arm7m
MOV shift, #0
; shift=0;
CMP x, #1 << 16 ; if (x < (1 << 16))
MOVCC x, x, LSL#16 ;
{ x = x << 16;
ADDCC shift, shift, #16 ; shift+=16; }
TST x, #0xFF000000 ; if (x < (1 << 24))
MOVEQ x, x, LSL#8 ;
{ x = x << 8;
ADDEQ shift, shift, #8 ; shift+=8; }
TST x, #0xF0000000 ; if (x < (1 << 28))
MOVEQ x, x, LSL#4 ;
{ x = x << 4;
ADDEQ shift, shift, #4 ; shift+=4; }
TST x, #0xC0000000 ; if (x < (1 << 30))
MOVEQ x, x, LSL#2 ;
{ x = x << 2;
ADDEQ shift, shift, #2 ; shift+=2; }
TST x, #0x80000000 ; if (x < (1 << 31))
ADDEQ shift, shift, #1 ; { shift+=1;
MOVEQS x, x, LSL#1 ; x << =1;
MOVEQ shift, #32
; if (x==0) shift=32; }
MOV pc, lr如果您使用的是ARM7TDMI或ARM9TDMI等ARMv4架构处理器,最终的MOVEQ指令在x为零时将shift设置为32,并且经常可以省略。这种实现在ARM7TDMI或ARM9TDMI上需要17个周期,足够满足大多数需求。然而,这并不是在这些处理器上归一化的最快方式。为了实现最快的归一化速度,可以使用基于哈希的方法。

基于哈希的方法首先将输入操作数减少到33种不同的可能性之一,而不改变CLZ值。我们通过对移位s = 1、2、4、8迭代执行x = x | (x >> s)来实现这一点。这将导致最高位的1向右复制16次。然后我们计算x & ~(x >> 16)。这将清除复制的16个1右侧的16个比特位。表格7.1说明了这些操作的综合效果。对于每个可能的输入二进制模式,我们展示了这些操作生成的32位代码。请注意,输入模式的CLZ值与代码的CLZ值相同。
现在我们的目标是使用哈希函数和查找表从代码值获取CLZ值。有关哈希函数的详细信息,请参见第6.8.2节。
对于哈希函数,我们将乘以一个大的值,并提取结果的前六位。形如2a + 1和2a - 1的值在ARM上使用移位器进行乘法非常容易。事实上,乘以(29 - 1)(211 - 1)(214 - 1)会为每个不同的CLZ值给出不同的哈希值。作者通过计算搜索找到了这个乘法器。
您可以使用此代码在ARMv4处理器上实现基于哈希的快速归一化。该实现在ARM7TDMI上需要13个周期(不包括设置表指针的时间)。
table RN 2 ; address of hash lookup table
;__value_in_regs struct { unsigned x; int shift; }
; unorm_arm7m_hash(unsigned x)
unorm_arm7m_hash
ORR shift, x, x, LSR#1
ORR shift, shift, shift, LSR#2
ORR shift, shift, shift, LSR#4
ORR shift, shift, shift, LSR#8
BIC shift, shift, shift, LSR#16
RSB shift, shift, shift, LSL#9 ; *(2∧9-1)
RSB shift, shift, shift, LSL#11 ; *(2∧11-1)
RSB shift, shift, shift, LSL#14 ; *(2∧14-1)
ADR table, unorm_arm7m_hash_table
LDRB shift, [table, shift, LSR#26]
MOV x, x, LSL shift
MOV pc, lr
unorm_arm7m_hash_table
DCB 0x20, 0x14, 0x13, 0xff, 0xff, 0x12, 0xff, 0x07
DCB 0x0a, 0x11, 0xff, 0xff, 0x0e, 0xff, 0x06, 0xff
DCB 0xff, 0x09, 0xff, 0x10, 0xff, 0xff, 0x01, 0x1a
DCB 0xff, 0x0d, 0xff, 0xff, 0x18, 0x05, 0xff, 0xff
DCB 0xff, 0x15, 0xff, 0x08, 0x0b, 0xff, 0x0f, 0xff
DCB 0xff, 0xff, 0xff, 0x02, 0x1b, 0x00, 0x19, 0xff
DCB 0x16, 0xff, 0x0c, 0xff, 0xff, 0x03, 0x1c, 0xff
DCB 0x17, 0xff, 0x04, 0x1d, 0xff, 0xff, 0x1e, 0x1f7.2.3 Counting Trailing Zeros
末尾零位计数(Count trailing zeros)是与首位零位计数(count leading zeros)相关的操作。它计算整数中最低有效置位位下方的零位数量。等价地,这可以检测整数的最高幂次的二次方。因此,可以通过计算末尾零位来将一个整数表示为2的幂次和一个奇数的乘积。如果整数为零,则没有最低位,因此末尾零位计数返回32。

要找到一个非零整数n的最高幂次的二次方,有一个技巧。技巧在于观察到表达式(n &(-n))在n中最低位位置上有一个单独的位被置位。图7.2展示了这个技巧的工作原理。其中,x表示通配符位。
使用这个技巧,我们可以将末尾零位计数转换为首位零位计数。以下代码在ARM9E上实现了末尾零位计数。我们通过使用条件指令来处理零输入情况,以避免额外的开销。
; unsigned ctz_arm9e(unsigned x)
ctz_arm9e
RSBS shift, x, #0 ; shift=-x
AND shift, shift, x ; isolate trailing 1 of x
CLZCC shift, shift ; number of zeros above last 1
RSC r0, shift, #32 ; number of zeros below last 1
MOV pc, lr对于没有CLZ指令的处理器,类似于7.2.2节中的哈希方法可以获得良好的性能:
; unsigned ctz_arm7m(unsigned x)
ctz_arm7m
RSB shift, x, #0
AND shift, shift, x
; isolate lowest bit
ADD shift, shift, shift, LSL#4 ; *(2∧4+1)
ADD shift, shift, shift, LSL#6 ; *(2∧6+1)
RSB shift, shift, shift, LSL#16 ; *(2∧16-1)
ADR table, ctz_arm7m_hash_table
LDRB r0, [table, shift, LSR#26]
MOV pc, lr
ctz_arm7m_hash_table
DCB 0x20, 0x00, 0x01, 0x0c, 0x02, 0x06, 0xff, 0x0d
DCB 0x03, 0xff, 0x07, 0xff, 0xff, 0xff, 0xff, 0x0e
DCB 0x0a, 0x04, 0xff, 0xff, 0x08, 0xff, 0xff, 0x19
DCB 0xff, 0xff, 0xff, 0xff, 0xff, 0x15, 0x1b, 0x0f
DCB 0x1f, 0x0b, 0x05, 0xff, 0xff, 0xff, 0xff, 0xff
DCB 0x09, 0xff, 0xff, 0x18, 0xff, 0xff, 0x14, 0x1a
DCB 0x1e, 0xff, 0xff, 0xff, 0xff, 0x17, 0xff, 0x13
DCB 0x1d, 0xff, 0x16, 0x12, 0x1c, 0x11, 0x107.3 Division
ARM核心没有硬件支持除法运算。要进行除法运算,必须调用一个使用标准算术运算符计算结果的软件程序。如果无法避免除法(请参见第5.10节以了解如何避免除法和通过重复分母进行快速除法),那么您需要访问经过高度优化的除法程序。本节提供一些有用的优化除法程序。
在ARM9E上,经过积极优化的牛顿-拉弗森(Newton-Raphson)除法程序每个周期运行速度与硬件除法实现相当。因此,ARM不需要复杂的硬件除法实现。
本节描述了我们所知道的最快的除法实现。由于有许多不同的除法技术和精度需要考虑,本节的长度不可避免地很长。我们还将证明这些程序确实适用于所有可能的输入。这是必要的,因为我们不能为32位乘以32位的除法尝试所有可能的输入参数!如果您对理论细节不感兴趣,可以跳过证明部分,直接从文本中获取代码。
7.3.1节介绍了使用试减法或二分查找的除法实现。当由于小商而可能出现早期终止时,试减法很有用,或者在处理器核心中没有快速乘法指令时。7.3.2节和7.3.3节介绍了使用牛顿-拉弗森迭代收敛到结果的实现。当最坏情况性能很重要或者存在快速乘法指令时,使用牛顿-拉弗森迭代。牛顿-拉弗森实现使用ARMv5TE扩展。最后,7.3.4节讨论有符号除法而不是无符号除法。
我们需要区分整数除法和真正的数学除法。让我们固定以下符号:
- n/d = 结果的整数部分,向零舍入(与C语言相同)
- n%d = 整数余数 n - d(n/d)(与C语言相同)
- n//d = nd-1 = n除以d的真正数学结果
7.3.1 Unsigned Division by Trial Subtraction
//无符号试减法除法
假设我们需要计算无符号整数n和d的商q = n/d以及余数r = n % d。同时假设我们知道商q适合N位,即 n/d < 2^N,或者等价地说n < (d << N)。试减法算法通过逐个尝试设置每个位来计算q的N位,从最高位开始,即第N-1位。这等效于对结果进行二分查找。如果我们可以从当前余数中减去(d << k)而不产生负数结果,就可以设置第k位。示例udiv_simple给出了此算法的简单C实现:
unsigned udiv_simple(unsigned d, unsigned n, unsigned N)
{
unsigned q=0, r=n;
do
{
/* calculate next quotient bit */
N--;
/* move to next bit */
if ( (r >> N) >= d ) /* if r>=d*(1 << N) */
{
r -= (d << N); /* update remainder */
q += (1 << N); /* update quotient */
}
} while (N);
return q;
}为了证明答案的正确性,注意在我们递减N之前,等式(7.1)的不变量成立:
![]()
初始时,q = 0且r = n,根据我们假设商适合N位,因此不变式成立。现在假设对于某个N,不变式保持成立。如果r<d^(2N−1),则我们不需要做任何操作使得不变式在N-1上保持成立。如果r ≥ d^(2N−1),则通过从r中减去d^(2N−1)并将2^(N−1)加到q上来保持不变式成立。
前述的实现称为恢复试减法实现。在非恢复式实现中,总是进行减法操作。然而,如果r变为负数,则在下一轮中使用加法(d N)而不是减法,以得到相同的结果。非恢复式除法在ARM上速度较慢,因此我们不会详细介绍。以下子节给出了用于不同被除数和除数大小的试减法的汇编实现。它们可以在任何ARM处理器上运行。
7.3.1.1 Unsigned 32-Bit/32-Bit Divide by Trial Subtraction
这是C编译器所需的操作。当在C中出现表达式n/d或n%d,并且d不是2的幂时,它将被调用。该例程返回一个由商和余数组成的两个元素的结构体。
d RN 0 ; input denominator d, output quotient
r RN 1 ; input numerator n, output remainder
t RN 2 ; scratch register
q RN 3 ; current quotient
; __value_in_regs struct { unsigned q, r; }
; udiv_32by32_arm7m(unsigned d, unsigned n)
udiv_32by32_arm7m
MOV q, #0
; zero quotient
RSBS t, d, r, LSR#3 ; if ((r >> 3)>=d) C=1; else C=0;
BCC div_3bits
; quotient fits in 3 bits
RSBS t, d, r, LSR#8 ; if ((r >> 8)>=d) C=1; else C=0;
BCC div_8bits
; quotient fits in 8 bits
MOV d, d, LSL#8 ; d = d*256
ORR q, q, #0xFF000000 ; make div_loop iterate twice
RSBS t, d, r, LSR#4 ; if ((r >> 4)>=d) C=1; else C=0;
BCC div_4bits
; quotient fits in 12 bits
RSBS t, d, r, LSR#8 ; if ((r >> 8)>=d) C=1; else C=0;
BCC div_8bits
; quotient fits in 16 bits
MOV d, d, LSL#8 ; d = d*256
ORR q, q, #0x00FF0000 ; make div_loop iterate 3 times
RSBS t, d, r, LSR#8 ; if ((r >> 8)>=d)
MOVCS d, d, LSL#8
;{d= d*256;
ORRCS q, q, #0x0000FF00 ; make div_loop iterate 4 times}
RSBS t, d, r, LSR#4 ; if ((r >> 4)<d)
BCC div_4bits
; r/d quotient fits in 4 bits
RSBS t, d, #0
; if (0 >= d)
BCS div_by_0
; goto divide by zero trap
; fall through to the loop with C=0
div_loop
MOVCS d, d, LSR#8 ; if (next loop) d = d/256
div_8bits
; calculate 8 quotient bits
RSBS t, d, r, LSR#7 ; if ((r >> 7)>=d) C=1; else C=0;
SUBCS r, r, d, LSL#7 ; if (C) r -= d << 7;
ADC q, q, q
; q=(q << 1)+C;
RSBS t, d, r, LSR#6 ; if ((r >> 6)>=d) C=1; else C=0;
SUBCS r, r, d, LSL#6 ; if (C) r -= d << 6;
ADC q, q, q
; q=(q << 1)+C;
RSBS t, d, r, LSR#5 ; if ((r >> 5)>=d) C=1; else C=0;
SUBCS r, r, d, LSL#5 ; if (C) r -= d << 5;
ADC q, q, q
; q=(q << 1)+C;
RSBS t, d, r, LSR#4 ; if ((r >> 4)>=d) C=1; else C=0;
SUBCS r, r, d, LSL#4 ; if (C) r -= d << 4;
ADC q, q, q
; q=(q << 1)+C;
div_4bits
; calculate 4 quotient bits
RSBS t, d, r, LSR#3 ; if ((r >> 3)>=d) C=1; else C=0;
SUBCS r, r, d, LSL#3 ; if (C) r -= d << 3;
ADC q, q, q
; q=(q << 1)+C;
div_3bits
; calculate 3 quotient bits
RSBS t, d, r, LSR#2 ; if ((r >> 2)>=d) C=1; else C=0;
SUBCS r, r, d, LSL#2 ; if (C) r -= d << 2;
ADC q, q, q
; q=(q << 1)+C;
RSBS t, d, r, LSR#1 ; if ((r >> 1)>=d) C=1; else C=0;
SUBCS r, r, d, LSL#1 ; if (C) r -= d << 1;
ADC q, q, q
; q=(q << 1)+C;
RSBS t, d, r
; if (r>=d) C=1; else C=0;
SUBCS r, r, d
; if (C) r -= d;
ADCS q, q, q
; q=(q << 1)+C; C=old q bit 31;
div_next
BCS div_loop
; loop if more quotient bits
MOV r0, q
; r0 = quotient; r1=remainder;
MOV pc, lr
; return { r0, r1 } structure;
div_by_0
MOV r0, #-1
MOV r1, #-1
MOV pc, lr
; return { -1, -1 } structure;要了解这个例程的工作原理,首先看一下在标签div_8bits和div_next之间的代码。这段代码计算8位商r/d,将余数保存在r中,并将商的8位插入到q的低位中。该代码使用了试减法算法。它尝试从r中依次减去128d、64d、32d、16d、8d、4d、2d和d。对于每次减法操作,如果减法是可行的,则将carry设置为1,否则为0。这个carry构成了要插入到q中的下一个结果位。
接下来注意,我们可以从div_4bits或div_3bits进入该代码,如果我们只想进行4位或3位的除法运算。
现在看一下例程的开头。我们希望计算r/d,将余数保存在r中,并将商写入q。我们首先检查商q是否能容纳3位或8位。如果是的话,我们可以直接跳转到div_3bits或div_8bits,分别计算出结果。这种提前终止在C语言中很有用,因为商通常较小。如果商需要超过8位,那么我们将d乘以256,直到r/d能够容纳8位为止。我们记录了我们通过高位的q将d乘以256的次数,每次乘法设置8位。这意味着在计算完8位r/d之后,我们会回到div_loop并为前面每次乘法都将d除以256。通过这种方式,我们将除法转化为一系列的8位除法。
7.3.1.2 Unsigned 32/15-Bit Divide by Trial Subtraction
在第7.3.1.1节中的32/32除法中,每次试减法操作需要每位商三个周期。然而,如果我们将分母和商限制为15位,那么每位商的试减法操作只需要两个周期。您会发现这种操作在16位DSP中非常有用,因为两个正Q15数的除法需要进行30/15位整数除法(参见第8.1.5节)。
在下面的代码中,被除数n是一个32位无符号整数。分母d是一个15位无符号整数。该例程返回一个包含15位商q和余数r的结构体。如果n ≥ (d << 15),那么结果会溢出,我们返回最大可能的商0x7fff。
m RN 0 ; input denominator d then (-d << 14)
r RN 1 ; input numerator n then remainder
; __value_in_regs struct { unsigned q, r; }
; udiv_32by16_arm7m(unsigned d, unsigned n)
udiv_32by16_arm7m
RSBS m, m, r, LSR#15
; m = (n >> 15) - d
BCS overflow_15
; overflow if (n >> 15)>=d
SUB m, m, r, LSR#15
; m = -d
MOV m, m, LSL#14
; m = -d << 14
; 15 trial division steps follow
ADDS r, m, r
; r=r-(d << 14); C=(r>=0);
SUBCC r, r, m
; if (C==0) r+=(d << 14)
ADCS r, m, r, LSL #1
; r=(2*r+C)-(d << 14); C=(r>=0);
SUBCC r, r, m
; if (C==0) r+=(d << 14)
ADCS r, m, r, LSL #1
; ... and repeat ...
SUBCC r, r, m
ADCS r, m, r, LSL #1
SUBCC r, r, m
ADCS r, m, r, LSL #1
SUBCC r, r, m
ADCS r, m, r, LSL #1
SUBCC r, r, m
ADCS r, m, r, LSL #1
SUBCC r, r, m
ADCS r, m, r, LSL #1
SUBCC r, r, m
ADCS r, m, r, LSL #1
SUBCC r, r, m
ADCS r, m, r, LSL #1
SUBCC r, r, m
ADCS r, m, r, LSL #1
SUBCC r, r, m
ADCS r, m, r, LSL #1
SUBCC r, r, m
ADCS r, m, r, LSL #1
SUBCC r, r, m
ADCS r, m, r, LSL #1
SUBCC r, r, m
ADCS r, m, r, LSL #1
SUBCC r, r, m
; extract answer and remainder (if required)
ADC r0, r, r
; insert final answer bit
MOV r, r0, LSR #15 ; extract remainder
BIC r0, r0, r, LSL #15 ; extract quotient
MOV pc, lr
; return { r0, r }
overflow_15
; quotient oveflows 15 bits
LDR r0, =0x7fff ; maximum quotient
MOV r1, r0
; maximum remainder
MOV pc, lr
; return { 0x7fff, 0x7fff }我们首先将m设置为-d214。与将分母的位移版本从余数中减去不同,我们将取负的分母加到位移后的余数中。在第k次试减法步骤之后,r的最低k位保存商的最高k位。r的上32-k位保存余数。每个ADC指令执行三个功能:
- 它将余数左移一位。
- 它插入最后一次试减法的下一个商位。
- 它从余数中减去d << 14。
经过15步操作,r的最低的15位包含商,而最高的17位包含余数。我们将它们分别记为r0和r1。除了返回之外,在ARM7TDMI上,该除法需要35个周期来完成。
7.3.1.3 Unsigned 64/31-Bit Divide by Trial Subtraction
这种操作在需要除以Q31定点整数时非常有用(参见第8.1.5节)。它可以使得在第7.3.1.2节中的除法精度加倍。被除数n是一个无符号64位整数,除数d是一个无符号的31位整数。下面的例程返回一个包含32位商q和余数r的结构体。如果n ≥ d^232,那么结果会溢出,我们返回最大可能的商0xffffffff。这个例程使用三位每周期试减法,在ARM7TDMI上需要99个周期。在代码注释中,我们使用[r, q]来表示一个64位值,其中高32位是r,低32位是q。
m RN 0 ; input denominator d, -d
r RN 1 ; input numerator (low), remainder (high)
t RN 2 ; input numerator (high)
q RN 3 ; result quotient and remainder (low)
; __value_in_regs struct { unsigned q, r; }
; udiv_64by32_arm7m(unsigned d, unsigned long long n)
udiv_64by32_arm7m
CMP t, m
; if (n >= (d << 32))
BCS overflow_32 ; goto overflow_32;
RSB m, m, #0 ; m = -d
ADDS q, r, r ; { [r,q] = 2*[r,q]-[d,0];
ADCS r, m, t, LSL#1 ; C = ([r,q]>=0); }
SUBCC r, r, m ; if (C==0) [r,q] += [d,0]
GBLA k
; the next 32 steps are the same
k SETA 1
; so we generate them using an
WHILE k<32
; assembler while loop
ADCS q, q, q ; { [r,q] = 2*[r,q]+C - [d,0];
ADCS r, m, r, LSL#1 ; C = ([r,q]>=0); }
SUBCC r, r, m ; if (C==0) [r,q] += [d,0]
k SETA k+1
WEND
ADCS r0, q, q ; insert final answer bit
MOV pc, lr ; return { r0, r1 }
overflow_32
MOV r0, #-1
MOV r1, #-1
MOV pc, lr ; return { -1, -1 }这个想法与32/15位除法类似。在第k次试减法后,64位值[r, q]包含最高的64-k位余数。最低的k位包含最高的k位商。经过32次试减法之后,r保存余数,q保存商。两个ADC指令将[r, q]左移一位,在底部插入最后一个答案位,并从上32位中减去分母。如果减法溢出,我们通过加回分母来修正余数r。
7.3.2 Unsigned Integer Newton-Raphson Division
//无符号整数的牛顿-拉弗森除法
牛顿-拉弗森迭代是一种用于数值求解方程的强大技术。一旦我们有了方程解的良好近似值,迭代将非常快速地收敛于该解。实际上,收敛通常是二次的,随着每次迭代有效小数位数的大约加倍。牛顿-拉弗森方法被广泛用于计算高精度的倒数和平方根。我们将使用牛顿-拉弗森方法来实现16位和32位整数和小数除法,尽管我们将要讨论的思想可以推广到任何大小的除法。
牛顿-拉弗森技术适用于任何形式为f(x) = 0的方程,其中f(x)是可微函数,其导数为f'(x)。我们从对方程的解x的近似值xn开始。然后我们应用以下迭代方法,以获得更好的近似值xn+1:


图7.3说明了用于求解f(x) = 0的牛顿-拉弗森迭代。以迅速收敛到解1.25。
我们选择x0 = 1作为初始近似值。前两个步骤是x1 = 1.2和x2 = 1.248。
对于许多函数f,迭代会迅速收敛到解x。从图形上看,我们将估计值xn+1放置在曲线在估计值xn处与x轴相交的位置上。
我们将使用牛顿-拉弗森迭代来仅使用整数乘法运算来计算2N d−1。我们允许乘以2N的因素,因为这在估计232/d时非常有用,正如第7.3.2.1节和第5.10.2节所使用的那样。考虑以下函数:

方程f(x) = 0在x = 2N d−1处有一个解,导数f'(x) = 2N x−2。
通过代入法,可以得到牛顿-拉弗森迭代的表达式:

从某种意义上说,迭代将我们的除法翻转了过来。我们不再乘以2N并除以d,而是现在乘以d并除以2N。有两种情况特别有用:
■ 当N = 32且d是一个整数时。在这种情况下,我们可以快速近似计算232d−1,并使用该近似值来计算n/d,即两个无符号32位数的比值。有关使用N = 32的迭代,请参见第7.3.2.1节。
■ 当N = 0且d是以固定点格式表示的分数,满足0.5 ≤ d < 1时。在这种情况下,我们可以使用迭代来计算d−1,这对于计算一系列固定点值n的nd−1很有用。有关使用N = 0的迭代,请参见第7.3.3节。
7.3.2.1 Unsigned 32/32-Bit Divide by Newton-Raphson
本节提供了一个替代第7.3.1.1节中常用例程的方法。以下例程具有非常好的最坏情况性能,并利用了ARM9E上更快的乘法器。我们使用N = 32和整数d的牛顿-拉弗森迭代来近似计算整数232/d。然后,我们将此近似值乘以n并除以232,得到商q = n/d的估计值。最后,我们计算余数r = n − qd,并根据任何舍入误差来纠正商和余数。
q RN 0 ; input denominator d, output quotient q
r RN 1 ; input numerator n, output remainder r
s RN 2 ; scratch register
m RN 3 ; scratch register
a RN 12 ; scratch register
; __value_in_regs struct { unsigned q, r; }
; udiv_32by32_arm9e(unsigned d, unsigned n)
udiv_32by32_arm9e ; instruction number : comment
CLZ s, q
; 01 : find normalizing shift
MOVS a, q, LSL s
; 02 : perform a lookup on the
ADD a, pc, a, LSR#25 ; 03 : most significant 7 bits
LDRNEB a, [a, #t32-b32-64] ; 04 : of divisor
b32 SUBS s, s, #7
; 05 : correct shift
RSB m, q, #0
; 06 : m = -d
MOVPL q, a, LSL s
; 07 : q approx (1 << 32)/d
; 1st Newton iteration follows
MULPL a, q, m
; 08:a= -q*d
BMI udiv_by_large_d ; 09 : large d trap
SMLAWT q, q, a, q
; 10 : q approx q-(q*q*d >> 32)
TEQ m, m, ASR#1
; 11 : check for d=0 or d=1
; 2nd Newton iteration follows
MULNE a, q, m
; 12:a= -q*d
MOVNE s, #0
; 13:s=0
SMLALNE s, q, a, q
; 14:q= q-(q*q*d >> 32)
BEQ udiv_by_0_or_1 ; 15 : trap d=0 or d=1
; q now accurate enough for a remainder r, 0<=r<3*d
UMULL s, q, r, q
; 16:q= (r*q) >> 32
ADD r, r, m
; 17 : r = n-d
MLA r, q, m, r
; 18 : r = n-(q+1)*d
; since 0 <= n-q*d < 3*d, thus -d <= r < 2*d
CMN r, m
; 19 : t = r-d
SUBCS r, r, m
; 20 : if (t<-d || t>=0) r=r+d
ADDCC q, q, #1
; 21 : if (-d<=t && t<0) q=q+1
ADDPL r, r, m, LSL#1 ; 22 : if (t>=0) { r=r-2*d
ADDPL q, q, #2
; 23 :
q=q+2 }
BX lr
; 24 : return {q, r}
udiv_by_large_d
; at this point we know d >= 2∧(31-6)=2∧25
SUB a, a, #4
; 25 : set q to be an
RSB s, s, #0
; 26 : underestimate of
MOV q, a, LSR s
; 27 : (1 << 32)/d
UMULL s, q, r, q
; 28:q= (n*q) >> 32
MLA r, q, m, r
; 29 : r = n-q*d
; q now accurate enough for a remainder r, 0<=r<4*d
CMN m, r, LSR#1
; 30 : if (r/2 >= d)
ADDCS r, r, m, LSL#1 ; 31 : { r=r-2*d;
ADDCS q, q, #2
; 32 : q=q+2; }
CMN m, r
; 33 : if (r >= d)
ADDCS r, r, m
; 34 : { r=r-d;
ADDCS q, q, #1
; 35 : q=q+1; }
BX lr
; 36 : return {q, r}
udiv_by_0_or_1
; carry set if d=1, carry clear if d=0
MOVCS q, r
; 37 : if (d==1) { q=n;
MOVCS r, #0
; 38 :
r=0; }
MOVCC q, #-1
; 39 : if (d==0) { q=-1;
MOVCC r, #-1
; 40 :
r=-1; }
BX lr
; 41 : return {q,r}
; table for 32 by 32 bit Newton Raphson divisions
; table[0] = 255
; table[i] = (1 << 14)/(64+i) for i=1,2,3,...,63
t32 DCB 0xff, 0xfc, 0xf8, 0xf4, 0xf0, 0xed, 0xea, 0xe6
DCB 0xe3, 0xe0, 0xdd, 0xda, 0xd7, 0xd4, 0xd2, 0xcf
DCB 0xcc, 0xca, 0xc7, 0xc5, 0xc3, 0xc0, 0xbe, 0xbc
DCB 0xba, 0xb8, 0xb6, 0xb4, 0xb2, 0xb0, 0xae, 0xac
DCB 0xaa, 0xa8, 0xa7, 0xa5, 0xa3, 0xa2, 0xa0, 0x9f
DCB 0x9d, 0x9c, 0x9a, 0x99, 0x97, 0x96, 0x94, 0x93
DCB 0x92, 0x90, 0x8f, 0x8e, 0x8d, 0x8c, 0x8a, 0x89
DCB 0x88, 0x87, 0x86, 0x85, 0x84, 0x83, 0x82, 0x81证明这段代码有效相当复杂。为了使证明和解释更简单,我们在每条指令上加上行号进行注释。请注意,其中一些指令是有条件的,注释只适用于执行该指令时。
根据分母d的大小,执行会按照代码中的几个不同路径进行。我们将这些情况分别处理。我们将使用Ik作为前述代码中编号为k的指令的简写符号。
情况1:d = 0,ARM9E芯片需要27个时钟周期,包括返回。
我们明确检查了这种情况。通过使加载在q ≠ 0时条件成立,我们避免了I04处的表查找。这确保我们不会读取表的开头。由于I01设置s = 32,因此在I09处没有分支跳转。I06设置m = 0,所以I11设置Z标志并清除进位标志。我们在I15处跳转到特殊情况代码。
情况2:d = 1,ARM9E芯片需要27个时钟周期,包括返回。
这种情况类似于d = 0的情况。I05处的表查找确实发生,但我们忽略了结果。I06设置m = -1,所以I11设置Z和进位标志。I37处的特殊代码返回了q = n,r = 0的平凡结果。
情况3:2 ≤ d < 225,ARM9E芯片需要36个时钟周期,包括返回。
这是最困难的情况。首先,我们使用d的前导位的表查找来生成232/d的估计值。I01找到一个移位s,使得231 ≤ d2s < 232。I02设置a = d2s。I03和I04对a的前七位进行表查找,我们将其称为i0。i0是介于64和127之间的索引。将d截断为七位会引入误差f0:


这是232d−1的一个很好的初始近似值,现在我们通过牛顿-拉弗逊迭代两次来增加近似值的精度。I08和I10根据方程(7.9)更新寄存器a和q的值为a1和q1。I08使用m = −d计算a1。由于d ≥ 2,所以当d = 2时q0 < 231,然后f0 = 0,i0 = 64,g0 = 1,e0 = 2−8。因此,我们可以在I10处使用带符号乘加指令SMLAWT来计算q1。

误差e3肯定是正的且很小,但有多小呢?我们将证明0 ≤ e3 < 3,通过证明e2 < d2−32。我们将其拆分为几个子情况:

情况3.1 2 ≤ d ≤ 16
在这种情况下,由于相应的截断没有丢弃任何位,所以f0 = f1 = g1 = 0。因此,e1 = e0/2,并且e0 = i0g02−14。我们可以在表格7.2中明确计算i0和g0。
情况3.2 16 < d ≤ 256
然后f0 ≤ 0.5意味着|e0| ≤ 2−7。由于f1 = g1 = 0,所以e2 < 2−28 < d2−32。
情况3.3 256 <d< 512
然后f0 ≤ 1意味着|e0| ≤ 2−6。由于f1 = g1 = 0,所以e2 < 2−24 < d2−32。
情况3.4 512 ≤ d < 225
然后f0 ≤ 1意味着|e0| ≤ 2−6。因此,e1 < 2−12 + 2−15 + d2−32。设D = √d2−32。那么2−11.5 ≤ D < 2−3.5。因此,e1 < D(2−0.5 + 2−3.5 + 2−3.5) < D,得到所需的结果。
现在我们知道e3 < 3,I16到I23计算了三个可能结果q3、q3 + 1、q3 + 2中哪一个是n/d的正确值。指令计算余数r = n − dq3,并且从余数中减去d,同时增加q,直到0 ≤ r < d。
情况4 225 ≤ d:在ARM9E上需要32个周期,包括返回
这种情况与情况3的开始方式相同。我们有相同的方程用于i0和a0。然而,然后我们在I25处分支,从a0中减去四,并进行一个右移7 − s。这给出了方程(7.15)中的估计q0。减去四迫使q0低估了232d−1。对于一些截断误差0 ≤ g0 < 1:


7.3.3 Unsigned Fractional Newton-Raphson Division
这一部分介绍了你可以用来进行分数除法的牛顿-拉弗森(Newton-Raphson)技术。分数值是使用定点算术表示的,对于DSP应用非常有用。
对于分数除法,我们首先将分母缩放到0.5 ≤ d < 1.0的范围内。然后我们使用查找表来提供对d−1的估计值x0。最后,我们使用N = 0进行牛顿-拉弗森迭代。根据第7.3.2节,迭代过程如下:
![]()
随着i的增加,xi变得更加准确。为了实现最快的计算,当i较小时我们使用低精度的乘法运算,并在每次迭代时增加精度。
结果是一个简短而高效的程序。第7.3.3.3节给出了一个用于15位分数除法的例程,而第7.3.3.4节则给出了一个用于31位分数除法的例程。同样,最困难的部分是证明我们对所有可能的输入都能得到正确的结果。对于31位除法,我们无法测试所有的分子和分母的组合。我们必须有一个代码可行性的证明。第7.3.3.1和7.3.3.2节涵盖了我们在第7.3.3.3和7.3.3.4节中所需的数学理论证明。如果你对这个理论不感兴趣,可以直接跳到第7.3.3.3节。
在整个分析过程中,我们坚持以下符号约定:
- d 是一个分数值,缩放后满足 0.5 ≤ d < 1。
- i 是迭代的阶段数。
- ki 是xi使用的精度位数。我们确保 ki+1 > ki ≥ 3。
- xi 是一个ki位的估计值,满足 0 ≤ xi ≤ 2 − 22−ki。
- xi 是 2^(1-ki) 的倍数。
- ei = d - xi 是逼近值xi的误差。我们确保 |ei| ≤ 0.5。
每次迭代时,我们增加ki并减小误差ei。首先让我们看看如何计算一个良好的初始估计值x0。
7.3.3.1 Theory: The Initial Estimate for Newton-Raphson Division
如果你对牛顿-拉弗森理论不感兴趣,可以跳过接下来的两节,直接跳到第7.3.3.3节。
为了确定初始估计值x0到d−1,我们使用一个查找表来处理d的最高有效位。为了在表的大小和估计精度之间获得良好的平衡,我们使用d的前八个小数位作为索引,返回一个九位的估计值x0。由于d和x0的前导位都是1,因此我们只需要一个由128个八位条目组成的查找表。
假设a是由d的前导1后面的七位组成的整数。那么d的范围是 (128 + a)2−8 ≤ d < (129 + a)2−8。选择 c = (128.5 + a)2−8 作为中点,我们通过以下公式定义查找表:
table[a] = round(256.0/c) - 256;
这是一个浮点数公式,其中 round 表示四舍五入到最近的整数。如果你没有浮点数支持,我们可以将其简化为更容易计算的整数公式:
table[a] = (511*(128-a))/(257+2*a);
显然,所有的表项都在0到255的范围内。为了开始牛顿-拉弗森迭代,我们设置 x0 = 1 + table[a]2−8 并且 k0 = 9。现在我们稍微提前看一下第7.3.3.3节的内容。我们将对以下误差项的值感兴趣:

7.3.3.2 Theory: Accuracy of the Newton-Raphson Fraction Iteration
这一节分析了每个小数牛顿-拉弗森迭代引入的误差:
xi+1 = 2xi − dxi^2 (7.26)
精确计算这个迭代通常是很慢的。由于xi的精度最多为ki,所以计算超过2ki位的精度没有太大意义。以下步骤给出了一种实际计算迭代的方法。这些迭代保持了我们在第7.3.3节中定义的xi和ei的限制条件。

7.3.3.3 Q15 Fixed-Point Division by Newton-Raphson
我们计算一个Q15表示的比值nd−1,其中n和d是16位的正整数,范围为0 ≤ n < d < 215。换句话说,我们计算
q = (n << 15)/d;
你可以使用第7.3.1.2节中的udiv_32by16_arm7m例程通过试减法来进行计算。然而,以下例程计算完全相同的结果,但在ARMv5E核心上使用更少的周期。如果你只需要结果的估计值,那么你可以删除指令I15到I18,这些指令纠正了初始估计的误差。
该例程在许多地方都接近不准确,因此后面跟着证明它的正确性。证明使用了第7.3.3.2节的理论。如果代码需要适应或优化为另一个ARM核心,该证明将是一个有用的参考。该例程在ARM9E上需要24个周期,包括返回指令。如果d ≤ n < 215,则返回饱和值0x7fff。
q RN 0 ; input denominator d, quotient estimate q
r RN 1 ; input numerator n, remainder r
s RN 2 ; normalisation shift, scratch
d RN 3 ; Q15 normalised denominator 2∧14<=d<2∧15
; unsigned udiv_q15_arm9e(unsigned d, unsigned q)
udiv_q15_arm9e ; instruction number : comment
CLZ s, q
; 01 : choose a shift s to
SUB s, s, #17
; 02 : normalize d to the
MOVS d, q, LSL s
; 03 : range 0.5<=d<1 at Q15
ADD q, pc, d, LSR#7 ; 04 : look up q, a Q8
LDRNEB q, [q, #t15-b15-128] ; 05 : approximation to 1//d
b15 MOV r, r, LSL s ; 06 : normalize numerator
ADD q, q, #256
; 07 : part of table lookup
; q is now a Q8, 9-bit estimate to 1//d
SMULBB s, q, q
; 08 : s = q*q at Q16
CMP r, d
; 09 : check for overflow
MUL s, d, s
; 10 : s = q*q*d at Q31
MOV q, q, LSL#9
; 11 : change q to Q17
SBC q, q, s, LSR#15 ; 12:q= 2*q-q*q*d at Q16
; q is now a Q16, 17-bit estimate to 1//d
SMULWB q, q, r
; 13 : q approx n//d at Q15
BCS overflow_15
; 14 : trap overflow case
SMULBB s, q, d
; 15 : s = q*d at Q30
RSB r, d, r, LSL#15 ; 16 : r = n-d at Q30
CMP r, s
; 17 : if (r>=s)
ADDPL q, q, #1
; 18 : q++
BX lr
; 19 : return q
overflow_15
LDR q, =0x7FFF
; 20:q= 0x7FFF
BX lr
; 21 : return q
; table for fractional Newton-Raphson division
; table[a] = (int)((511*(128-a))/(257+2*a)) 0<=a<128
t15 DCB 0xfe, 0xfa, 0xf6, 0xf2, 0xef, 0xeb, 0xe7, 0xe4
DCB 0xe0, 0xdd, 0xd9, 0xd6, 0xd2, 0xcf, 0xcc, 0xc9
DCB 0xc6, 0xc2, 0xbf, 0xbc, 0xb9, 0xb6, 0xb3, 0xb1
DCB 0xae, 0xab, 0xa8, 0xa5, 0xa3, 0xa0, 0x9d, 0x9b
DCB 0x98, 0x96, 0x93, 0x91, 0x8e, 0x8c, 0x8a, 0x87
DCB 0x85, 0x83, 0x80, 0x7e, 0x7c, 0x7a, 0x78, 0x75
DCB 0x73, 0x71, 0x6f, 0x6d, 0x6b, 0x69, 0x67, 0x65
DCB 0x63, 0x61, 0x5f, 0x5e, 0x5c, 0x5a, 0x58, 0x56
DCB 0x54, 0x53, 0x51, 0x4f, 0x4e, 0x4c, 0x4a, 0x49
DCB 0x47, 0x45, 0x44, 0x42, 0x40, 0x3f, 0x3d, 0x3c
DCB 0x3a, 0x39, 0x37, 0x36, 0x34, 0x33, 0x32, 0x30
DCB 0x2f, 0x2d, 0x2c, 0x2b, 0x29, 0x28, 0x27, 0x25
DCB 0x24, 0x23, 0x21, 0x20, 0x1f, 0x1e, 0x1c, 0x1b
DCB 0x1a, 0x19, 0x17, 0x16, 0x15, 0x14, 0x13, 0x12
DCB 0x10, 0x0f, 0x0e, 0x0d, 0x0c, 0x0b, 0x0a, 0x09
DCB 0x08, 0x07, 0x06, 0x05, 0x04, 0x03, 0x02, 0x01证明:
该例程首先通过指令I01、I02、I03、I06对d和n进行归一化处理,以使得214 ≤ d < 215。由于我们将分子和分母左移相同的位数,这不会影响结果。将d视为Q15格式的定点小数,其中0.5 ≤ d < 1。
指令I09和I14是溢出陷阱,用于捕捉n ≥ d的情况。这包括了d = 0的情况。假设从现在开始没有溢出,指令I04、I05、I07根据第7.3.1.1节的描述,将q设置为9位Q8初始估计值x0到d−1。由于d在范围0.5 ≤ d < 1内,我们在表查找时减去128,使得0.5对应于表的第一个条目。
接下来,我们执行一次牛顿-拉弗森迭代。指令I08将a设置为x0的精确Q16平方,指令I10将a设置为dx0^2的精确Q31值。这里有一个微妙之处。我们需要检查这个值是否会溢出无符号Q31表示。实际上:


7.3.3.4 Q31 Fixed-Point Division by Newton-Raphson
我们计算nd−1的Q31比例表示,其中n和d是32位正整数,范围为0 ≤ n<d< 231。换句话说,我们计算
q = (unsigned int)(((unsigned long long)n << 31)/d);
您可以使用第7.3.1.3节中的udiv_64by32_arm7m例程通过试减法来完成这个计算。然而,下面的例程计算出完全相同的结果,但在ARM9E上使用较少的周期。如果您只需要一个估计值,那么可以删除指令I21到I29,这些指令纠正了初始估计的错误。
与前一节一样,我们先展示汇编代码,然后进行正确性证明。该例程在ARM9E上使用46个周期,包括返回。该例程使用的查找表与第7.3.3.3节中的Q15例程相同。
q RN 0 ; input denominator d, quotient estimate q
r RN 1 ; input numerator n, remainder high r
s RN 2 ; normalization shift, scratch register
d RN 3 ; Q31 normalized denominator 2∧30<=d<2∧31
a RN 12 ; scratch
; unsigned udiv_q31_arm9e(unsigned d, unsigned q)
udiv_q31_arm9e ; instruction number : comment
CLZ s, q
; 01 : choose a shift s to
CMP r, q
; 02 : normalize d to the
MOVCC d, q, LSL s
; 03 : range 0.5<=d<1 at Q32
ADDCC q, pc, d, LSR#24 ; 04 : look up q, a Q8
LDRCCB q, [q, #t15-b31-128] ; 05 : approximation to 1//d
b31 MOVCC r, r, LSL s
; 06 : normalize numerator
ADDCC q, q, #256
; 07 : part of table lookup
; q is now a Q8, 9-bit estimate to 1//d
SMULBBCC a, q, q
; 08 : a = q*q at Q16
MOVCS q, #0x7FFFFFFF ; 09 : overflow case
UMULLCC s, a, d, a
; 10:a= q*q*d at Q16
BXCS lr
; 11 : exit on overflow
RSB q, a, q, LSL#9 ; 12:q= 2*q-q*q*d at Q16
; q is now a Q16, 17-bit estimate to 1//d
UMULL a, s, q, q
; 13 : [s,a] = q*q at Q32
MOVS a, a, LSR#1
; 14 : now halve [s,a] and
ADC a, a, s, LSL#31 ; 15 : round so [N,a]=q*q at
MOVS s, s, LSL#30 ; 16 : Q31, C=0
UMULL s, a, d, a
; 17 : a = a*d at Q31
ADDMI a, a, d
; 18 : if (N) a+=2*d at Q31
RSC q, a, q, LSL#16 ; 19:q= 2*q-q*q*d at Q31
; q is now a Q31 estimate to 1/d
UMULL s, q, r, q
; 20 : q approx n//d at Q31
; q is now a Q31 estimate to num/den, remainder<3*d
UMULL s, a, d, q
; 21 : [a,s] = d*q at Q62
RSBS s, s, #0
; 22 : [r,s] = n-d*q
RSC r, a, r, LSR#1 ; 23 : at Q62
; [r,s]=(r << 32)+s is now the positive remainder<3*d
SUBS s, s, d
; 24 : [r,s] = n-(d+1)*q
SBCS r, r, #0
; 25 : at Q62
ADDPL q, q, #1
; 26 : if ([r,s]>=0) q++
SUBS s, s, d
; 27 : [r,s] = [r,s]-d
SBCS r, r, #0
; 28 : at Q62
ADDPL q, q, #1
; 29 : if ([r,s]>=0) q++
BX lr
; 30 : return q证明:
我们首先检查n<d。如果不是,则会发生一系列的条件指令,在I11处返回饱和值0x7fffffff。否则,d和n将归一化为Q31表示,230 ≤ d < 231。如同在第7.3.3.3节中一样,I07将q设置为x0的Q8表示,即初始近似值。
I08、I10和I12实现了第一次牛顿-拉弗森迭代。I08将a设置为x0^2的Q16表示。I10将a设置为dx0^2 - g0的Q16表示,其中舍入误差满足0 ≤ g0 < 2^-16。I12将x设置为x1的Q16表示,即对d-1的新估计值。方程(7.33)告诉我们,该估计值的误差为e1 = de2^0 - g0。
I13到I19实现了第二次牛顿-拉弗森迭代。I13到I15将a设置为a1 = x2^1 + b1的Q31表示,其中b1为某个误差。由于我们在I15处使用了ADC指令,计算会向上舍入,因此0 ≤ b1 ≤ 2^-32。ADC指令不会溢出,因为233 - 1和234 - 1都不是完全平方数。然而,a1可能会溢出Q31表示。I16清除进位标志,并在N标志中记录溢出情况,以使a1 ≥ 2。I17和I18将a设置为y1 = da1 - c1的Q31表示,其中舍入误差0 ≤ c1 < 2^-31。由于进位标志被清除,I19将q设置为新的低估的Q31表示:

7.3.4 Signed Division
到目前为止,我们只讨论了无符号除法的实现。如果您需要对有符号值进行除法运算,则将其转换为无符号除法,并将符号重新加回结果中。商值只有在被除数和除数的符号相反时才为负。余数的符号与被除数的符号相同。以下示例展示了如何将有符号整数除法转化为无符号除法,并计算商和余数的符号。
d RN 0 ; input denominator, output quotient
r RN 1 ; input numerator , output remainder
sign RN 12
; __value_in_regs struct { signed q, r; }
; udiv_32by32_arm7m(signed d, signed n)
sdiv_32by32_arm7m
STMFD sp!, {lr}
ANDS sign, d, #1 << 31 ; sign=(d<0 ? 1 << 31 : 0);
RSBMI d, d, #0
; if (d<0) d=-d;
EORS sign, sign, r, ASR#32 ; if (r<0) sign=∼sign;
RSBCS r, r, #0
; if (r<0) r=-r;
BL udiv_32by32_arm7m ; (d,r)=(r/d,r%d)
MOVS sign, sign, LSL#1 ; C=sign[31], N=sign[30]
RSBCS d, d, #0
; if (sign[31]) d=-d;
RSBMI r, r, #0
; if (sign[30]) r=-r;
LDMFD sp!, {pc}我们使用r12寄存器来保存商和余数的符号,因为udiv_32by32_arm7m会保留r12寄存器(参见第7.3.1.1节)。
7.4 Square Roots
平方根可以使用与除法相同的技术来处理。您可以选择使用试减法或基于牛顿-拉弗森迭代的实现方法。对于精度低于16位的低精度结果,可以使用试减法,但对于高精度结果,应切换到牛顿-拉弗森方法。分别在第7.4.1节和第7.4.2节中介绍了试减法和牛顿-拉弗森方法。
7.4.1 Square Root by Trial Subtraction
我们计算一个32位无符号整数d的平方根。答案是一个16位无符号整数q和一个17位无符号余数r,满足以下条件:
![]()
我们从设置q = 0和r = d开始。接下来,我们逐个尝试设置q的每个位,从最高位bit 15开始递减。如果新的余数是正数,我们可以设置该位。具体来说,如果通过将2^n添加到q来设置第n位,那么新的余数将是:
![]()
因此,为了计算新的余数,我们试图减去值2n(2q + 2n)。如果减法成功并得到非负结果,则设置q的第n位。以下是C代码示例,说明了计算2N位输入d的N位平方根q的算法:
unsigned usqr_simple(unsigned d, unsigned N)
{
unsigned t, q=0, r=d;
do
{
/* calculate next quotient bit */
N--;
/* move down to next bit */
t = 2*q+(1 << N); /* new r = old r - (t << N) */
if ( (r >> N) >= t ) /* if (r >= (t << N)) */
{
r -= (t << N); /* update remainder */
q += (1 << N); /* update root */
}
} while (N);
return q;
}使用以下优化的汇编代码来实现前面的算法,只需50个周期,包括返回。关键在于在计算答案的第N位之前,寄存器q保存值(1 << 30)|(q >> (N + 1))。如果我们将该值左旋转2N + 2位,或者等效地右旋转30 − 2N位,那么我们就得到了之前用于试减的值t<<N。
q RN 0 ; input value, current square root estimate
r RN 1 ; the current remainder
c RN 2 ; scratch register
usqr_32 ; unsigned usqr_32(unsigned q)
SUBS r, q, #1 << 30
; is q>=(1 << 15)∧2?
ADDCC r, r, #1 << 30
; if not restore
MOV c, #3 << 30
; c is a constant
ADC q, c, #1 << 31
; set bit 15 of answer
; calculate bits 14..0 of the answer
GBLA N
N SETA 14
WHILE N< >-1
CMP r, q, ROR #(30-2*N) ; is r >= t << N ?
SUBCS r, r, q, ROR #(30-2*N) ; if yes then r -= t << N;
ADC q, c, q, LSL#1
; insert next bit of answer
N SETA (N-1)
WEND
BIC q, q, #3 << 30
; extract answer
MOV pc, lr7.4.2 Square Root by Newton-Raphson Iteration
牛顿-拉弗逊迭代法实际上计算的是值d-0.5的结果,而不是平方根本身。你可能会发现这个结果比平方根本身更有用。例如,要对一个向量(x, y)进行归一化,你可以乘以该向量的倒数的平方根。

如果你确实需要√d,那么只需要将d-0.5乘以d即可。方程f(x) = d-x-2 = 0有一个正解x = d-0.5。用于求解这个方程的牛顿-拉弗逊迭代法如下(参见7.3.2节):
![]()
要实现这个方法,你可以使用我们在7.3.2节中讨论过的相同方法。首先将d归一化到范围0.25 ≤ d < 1。然后使用表格查找d的前导数字生成初始估计x0。迭代上述公式,直到达到你的应用所需的精度。每次迭代将大致使结果精确位数翻倍。 以下代码计算了一个输入整数d的值d-0.5的Q31表示。它使用表格查找,然后进行两次牛顿-拉弗逊迭代,并且在最大误差为2^-29的情况下是准确的。在ARM9E上,该代码需要34个周期,包括返回。
q RN 0 ; input value, estimated reciprocal root
b RN 1 ; scratch register
s RN 2 ; normalization shift
d RN 3 ; normalized input value
a RN 12 ; scratch register/accumulator
rsqr_32 ; unsigned rsqr_32(unsigned q)
CLZ s, q
; choose shift s which is
BIC s, s, #1
; even such that d=(q << s)
MOVS d, q, LSL s ; is 0.25<=d<1 at Q32
ADDNE q, pc, d, LSR#25 ; table lookup on top 7 bits
LDRNEB q, [q, #tab-base-32] ; of d in range 32 to 127
base BEQ div_by_zero ; divide by zero trap
ADD q, q, #0x100 ; table stores only bottom 8 bits
; q is now a Q8, 9-bit estimate to 1/sqrt(d)
SMULBB a, q, q
; a = q*q at Q16
MOV b, d, LSR #17 ; b = d at Q15
SMULWB a, a, b
; a = d*q*q at Q15
MOV b, q, LSL #7 ; b = q at Q15
RSB a, a, #3 << 15 ; a = (3-d*q*q) at Q15
MUL q, a, b
; q = q*(3-d*q*q)/2 at Q31
; q is now a Q31 estimate to 1/sqrt(d)
UMULL b, a, d, q
; a = d*q at Q31
MOV s, s, LSR #1 ; square root halves the shift
UMULL b, a, q, a
; a = d*q*q at Q30
RSB s, s, #15
; reciprocal inverts the shift
RSB a, a, #3 << 30 ; a = (3-d*q*q) at Q30
UMULL b, q, a, q
; q = q*(3-d*q*q)/2 at Q31
; q is now a good Q31 estimate to 1/sqrt(d)
MOV q, q, LSR s ; undo the normalization shift
BX lr
; return q
div_by_zero
MOV q, #0x7FFFFFFF ; maximum positive answer
BX lr
; return q
tab ; tab[k] = round(256.0/sqrt((k+32.3)/128.0)) - 256
DCB 0xfe, 0xf6, 0xef, 0xe7, 0xe1, 0xda, 0xd4, 0xce
DCB 0xc8, 0xc3, 0xbd, 0xb8, 0xb3, 0xae, 0xaa, 0xa5
DCB 0xa1, 0x9c, 0x98, 0x94, 0x90, 0x8d, 0x89, 0x85
DCB 0x82, 0x7f, 0x7b, 0x78, 0x75, 0x72, 0x6f, 0x6c
DCB 0x69, 0x66, 0x64, 0x61, 0x5e, 0x5c, 0x59, 0x57
DCB 0x55, 0x52, 0x50, 0x4e, 0x4c, 0x49, 0x47, 0x45
DCB 0x43, 0x41, 0x3f, 0x3d, 0x3b, 0x3a, 0x38, 0x36
DCB 0x34, 0x32, 0x31, 0x2f, 0x2d, 0x2c, 0x2a, 0x29
DCB 0x27, 0x26, 0x24, 0x23, 0x21, 0x20, 0x1e, 0x1d
DCB 0x1c, 0x1a, 0x19, 0x18, 0x16, 0x15, 0x14, 0x13
DCB 0x11, 0x10, 0x0f, 0x0e, 0x0d, 0x0b, 0x0a, 0x09
DCB 0x08, 0x07, 0x06, 0x05, 0x04, 0x03, 0x02, 0x01类似地,要计算d的-k次方根d^(-1/k),可以使用牛顿-拉弗逊迭代法求解方程f(x) = d - x^(-k) = 0。
7.5 Transcendental Functions: log, exp, sin, cos
您可以通过使用表格查找和级数展开的组合来实现超越函数。我们来看一下最常见的四个超越运算:对数(log),指数(exp),正弦(sin)和余弦(cos)。在数字信号处理(DSP)应用中,对数和指数函数用于在线性和对数格式之间进行转换。而三角函数正弦和余弦在二维和三维图形以及映射计算中非常有用。
本节中的所有示例例程生成的答案精确到32位,这对于许多应用来说是过于精确的。您可以通过缩小级数展开的范围来加快性能,虽然会损失一些精度。
7.5.1 The Base-Two Logarithm
假设我们有一个32位整数n,并且我们想要找到以2为底的对数s = log2(n),使得n = 2^s。由于s在范围0 ≤ s < 32内,我们实际上会找到一个Q26表示q的对数,以便q = s * 2^26。我们可以使用CLZ或第7.2节中的其他方法轻松计算s的整数部分。这将将我们限制在区间1 ≤ n < 2内。首先,我们对近似值a进行表格查找,以找到log2(a)和a−1。


其中ln表示以e为底的自然对数。总结起来,我们通过以下三个阶段计算对数,如图7.4所示:
■ 使用CLZ找到结果的位[31:26]。
■ 使用前五个小数位的表格查找来找到一个近似值。
■ 使用级数展开更准确地计算近似值的误差。
您可以使用以下代码在ARM9E处理器上实现这一过程,其中31个周期不包括返回。答案的误差精度为2的-25次方。
n RN 0 ; Q0 input, Q26 log2 estimate
d RN 1 ; normalize input Q32
r RN 2
q RN 3
t RN 12
; int ulog2_32(unsigned n)
ulog2_32
CLZ r, n
MOV d, n, LSL#1
MOV d, d, LSL r ; 1<=d<2 at Q32
RSB n, r, #31
; integer part of the log
MOV r, d, LSR#27 ; estimate e=1+(r/32)+(1/64)
ADR t, ulog2_table
LDR r, [t, r, LSL#3]! ; r=log2(e) at Q26
LDR q, [t, #4]
; q=1/e at Q32
MOV t, #0
UMLAL t, r, d, r
; r=(d/e)-1 at Q32
LDR t, =0x55555555 ; round(2∧32/3)
ADD n, q, n, LSL#26 ; n+log2(e) at Q26
SMULL t, q, r, t
; q = r/3 at Q32
LDR d, =0x05c551d9 ; round(2∧26/ln(2))
SMULL t, q, r, q
;q=r∧2/3 at Q32
MOV t, #0
SUB q, q, r, ASR#1 ; q = -r/2+r∧2/3 at Q32
SMLAL t, r, q, r
;r-r∧2/2 + r∧3/3 at Q32
MOV t, #0
SMLAL t, n, d, r
; n += r/log(2) at Q26
MOV pc, lr
ulog2_table
; table[2*i] =round(2∧32/a) where a=1+(i+0.5)/32
; table[2*i+1]=round(2∧26*log2(a)) and 0<=i<32
DCD 0xfc0fc0fc, 0x0016e797, 0xf4898d60, 0x0043ace2
DCD 0xed7303b6, 0x006f2109, 0xe6c2b448, 0x0099574f
DCD 0xe070381c, 0x00c2615f, 0xda740da7, 0x00ea4f72
DCD 0xd4c77b03, 0x0111307e, 0xcf6474a9, 0x0137124d
DCD 0xca4587e7, 0x015c01a4, 0xc565c87b, 0x01800a56
DCD 0xc0c0c0c1, 0x01a33761, 0xbc52640c, 0x01c592fb
DCD 0xb81702e0, 0x01e726aa, 0xb40b40b4, 0x0207fb51
DCD 0xb02c0b03, 0x0228193f, 0xac769184, 0x0247883b
DCD 0xa8e83f57, 0x02664f8d, 0xa57eb503, 0x02847610
DCD 0xa237c32b, 0x02a20231, 0x9f1165e7, 0x02bef9ff
DCD 0x9c09c09c, 0x02db632d, 0x991f1a51, 0x02f7431f
DCD 0x964fda6c, 0x03129ee9, 0x939a85c4, 0x032d7b5a
DCD 0x90fdbc09, 0x0347dcfe, 0x8e78356d, 0x0361c825
DCD 0x8c08c08c, 0x037b40e4, 0x89ae408a, 0x03944b1c
DCD 0x8767ab5f, 0x03acea7c, 0x85340853, 0x03c52286
DCD 0x83126e98, 0x03dcf68e, 0x81020408, 0x03f469c27.5.2 Base-Two Exponentiation
这是第7.5.1节操作的逆过程。给定一个表示0 ≤ x < 32的Q26表示形式,我们计算以2为底的指数2^x。我们首先将x分为整数部分n和小数部分d。然后,2^x = 2^d × 2^n。要计算2^d,首先找到一个近似值a来表示d,并查找2^a。
接下来,

您可以使用以下汇编代码来实现上述算法。结果的最大误差为4。该程序在ARM9E上执行需要31个周期,不包括返回。
n RN 0 ; input, integer part
d RN 1 ; fractional part
r RN 2
q RN 3
t RN 12
; unsigned uexp2_32(int n)
uexp2_32
MOV d, n, LSL#6 ; d = fractional part at Q32
MOV q, d, LSR#27 ; estimate a=(q+0.5)/32
LDR r, =0xb17217f8 ; round(2∧32*log(2))
BIC d, d, q, LSL#27
;d=d- (q/32) at Q32
UMULL t, d, r, d ; d = d*log(2) at Q32
LDR t, =0x55555555 ; round(2∧32/3)
SUB d, d, r, LSR#6
;d=d- log(2)/64 at Q32
SMULL t, r, d, t ; r = d/3 at Q32
MOVS n, n, ASR#26 ; n = integer part of exponent
SMULL t, r, d, r
;r=d∧2/3 at Q32
BMI negative
; catch negative exponent
ADD r, r, d
; r = d+d∧2/3
SMULL t, r, d, r
;r=d∧2+d∧3/3
ADR t, uexp2_table
LDR q, [t, q, LSL#2] ; q = exp2(a) at Q31
ADDS r, d, r, ASR#1
; r = d+d∧2/2+d∧3/6 at Q32
UMULL t, r, q, r ; r = exp2(a)*r at Q31 if r<0
RSB n, n, #31
; 31-(integer part of exponent)
ADDPL r, r, q
; correct if r>0
MOV n, r, LSR n ; result at Q0
MOV pc, lr
negative
MOV r0, #0
; 2∧(-ve)=0
MOV pc, lr
uexp2_table
; table[i]=round(2∧31*exp2(a)) where a=(i+0.5)/32
DCD 0x8164d1f4, 0x843a28c4, 0x871f6197, 0x8a14d575
DCD 0x8d1adf5b, 0x9031dc43, 0x935a2b2f, 0x96942d37
DCD 0x99e04593, 0x9d3ed9a7, 0xa0b05110, 0xa43515ae
DCD 0xa7cd93b5, 0xab7a39b6, 0xaf3b78ad, 0xb311c413
DCD 0xb6fd91e3, 0xbaff5ab2, 0xbf1799b6, 0xc346ccda
DCD 0xc78d74c9, 0xcbec14ff, 0xd06333db, 0xd4f35aac
DCD 0xd99d15c2, 0xde60f482, 0xe33f8973, 0xe8396a50
DCD 0xed4f301f, 0xf281773c, 0xf7d0df73, 0xfd3e0c0d7.5.3 Trigonometric Operations
如果需要低精度的三角函数运算(通常用于生成正弦波和其他音频信号,或者用于图形处理),可以使用查找表。对于高精度图形或全球定位,可能需要更高的精度。我们在这里讨论的例程可以生成32位准确的正弦和余弦值。
标准C库函数sin和cos要求以弧度为单位指定角度。当处理优化的定点函数时,弧度作为单位选择是不方便的。首先,在任何角度相加时,需要在2π范围内执行算术模运算。其次,它需要涉及到π的范围检查,以确定一个角度位于圆的哪个象限。与其模2π运算,我们将模232运算,这是任何处理器上非常简单的操作。
让我们定义新的二进制基数三角函数s和c,其中角度是按照一个完整旋转(2π弧度或360度)为232来指定的。为了添加这些角度,我们使用标准的模整数加法:
![]()
在这个形式中,x是角度所表示的旋转比例的Q32表示。x的前两位告诉我们角度所在的圆的象限。首先,我们使用x的前三位将s(x)或c(x)减少到一个角度在零到1/8个旋转之间的正弦或余弦。然后,我们选择一个近似值a来代替x,并使用表格查找s(a)和c(a)的值。正弦和余弦的加法公式将问题简化为求解一个小角度的正弦和余弦:

您可以使用以下汇编代码来实现上述算法以计算正弦和余弦。结果以Q30格式返回,最大误差为4 × 2^(-30)。这个例程在ARM9E上执行需要31个周期,不包括返回。
n RN 0 ; the input angle in revolutions at Q32, result Q30
s RN 1 ; the output sign
r RN 2
q RN 3
t RN 12
cos_32 ; int cos_32(int n)
EOR s, n, n, LSL#1 ; cos is -ve in quadrants 1,2
MOVS n, n, LSL#1 ; angle in revolutions at Q33
RSBMI n, n, #0 ; in range 0-1/4 of a revolution
CMP n, #1 << 30 ; if angle < 1/8 of a revolution
BCC cos_core ; take cosine
SUBEQ n, n, #1 ; otherwise take sine of
RSBHI n, n, #1 << 31 ; (1/4 revolution)-(angle)
sin_core
; take sine of Q33 angle n
MOV q, n, LSR#25 ; approximation a=(q+0.5)/32
SUB n, n, q, LSL#25 ; n = n-(q/32) at Q33
SUB n, n, #1 << 24 ; n = n-(1/64) at Q33
LDR t, =0x6487ed51 ; round(2*PI*2∧28)
MOV r, n, LSL#3
; r = n at Q36
SMULL t, n, r, t ; n = (x-a)*PI/2∧31 at Q32
ADR t, cossin_tab
LDR q, [t, q, LSL#3]! ; c(a) at Q30
LDR t, [t, #4] ; s(a) at Q30
EOR q, q, s, ASR#31 ; correct c(a) sign
EOR s, t, s, ASR#31 ; correct s(a) sign
SMULL t, r, n, n ; n∧2 at Q32
SMULL t, q, n, q ; n*c(a) at Q30
SMULL t, n, r, s ; n∧2*s(a) at Q30
LDR t, =0xd5555556 ; round(-2∧32/6)
SUB n, s, n, ASR#1 ; n = s(a)*(1-n∧2/2) at Q30
SMULL t, s, r, t ; s=-n∧2/6
at Q32
ADD n, n, q
; n += c(a)*n at Q30
MOV t, #0
SMLAL t, n, q, s ; n += -c(a)*n∧3/6 at Q30
MOV pc, lr
; return n
sin_32;int sin_32(int n)
AND s, n, #1 << 31 ; sin is -ve in quadrants 2,3
MOVS n, n, LSL#1 ; angle in revolutions at Q33
RSBMI n, n, #0 ; in range 0-1/4 of a revolution
CMP n, #1 << 30 ; if angle < 1/8 revolution
BCC sin_core ; take sine
SUBEQ n, n, #1 ; otherwise take cosine of
RSBHI n, n, #1 << 31 ; (1/4 revolution)-(angle)
cos_core
; take cosine of Q33 angle n
MOV q, n, LSR#25 ; approximation a=(q+0.5)/32
SUB n, n, q, LSL#25 ; n = n-(q/32) at Q33
SUB n, n, #1 << 24 ; n = n-(1/64) at Q33
LDR t, =0x6487ed51 ; round(2*PI*2∧28)
MOV r, n, LSL#3
; r = n at Q26
SMULL t, n, r, t ; n = (x-a)*PI/2∧31 at Q32
ADR t, cossin_tab
LDR q, [t, q, LSL#3]! ; c(a) at Q30
LDR t, [t, #4] ; s(a) at Q30
EOR q, q, s, ASR#31 ; correct c(a) sign
EOR s, t, s, ASR#31 ; correct s(a) sign
SMULL t, r, n, n ; n∧2 at Q32
SMULL t, s, n, s ; n*s(a) at Q30
SMULL t, n, r, q ; n∧2*c(a) at Q30
LDR t, =0x2aaaaaab ; round(+2∧23/6)
SUB n, q, n, ASR#1 ; n = c(a)*(1-n∧2/2) at Q30
SMULL t, q, r, t ; n∧2/6 at Q32
SUB n, n, s
; n += -sin*n at Q30
MOV t, #0
SMLAL t, n, s, q ; n += sin*n∧3/6 at Q30
MOV pc, lr
; return n
cossin_tab
; table[2*i] =round(2∧30*cos(a)) where a=(PI/4)*(i+0.5)/32
; table[2*i+1]=round(2∧30*sin(a)) and 0 <= i < 32
DCD 0x3ffec42d, 0x00c90e90, 0x3ff4e5e0, 0x025b0caf
DCD 0x3fe12acb, 0x03ecadcf, 0x3fc395f9, 0x057db403
DCD 0x3f9c2bfb, 0x070de172, 0x3f6af2e3, 0x089cf867
DCD 0x3f2ff24a, 0x0a2abb59, 0x3eeb3347, 0x0bb6ecef
DCD 0x3e9cc076, 0x0d415013, 0x3e44a5ef, 0x0ec9a7f3
DCD 0x3de2f148, 0x104fb80e, 0x3d77b192, 0x11d3443f
DCD 0x3d02f757, 0x135410c3, 0x3c84d496, 0x14d1e242
DCD 0x3bfd5cc4, 0x164c7ddd, 0x3b6ca4c4, 0x17c3a931
DCD 0x3ad2c2e8, 0x19372a64, 0x3a2fcee8, 0x1aa6c82b
DCD 0x3983e1e8, 0x1c1249d8, 0x38cf1669, 0x1d79775c
DCD 0x3811884d, 0x1edc1953, 0x374b54ce, 0x2039f90f
DCD 0x367c9a7e, 0x2192e09b, 0x35a5793c, 0x22e69ac8
DCD 0x34c61236, 0x2434f332, 0x33de87de, 0x257db64c
DCD 0x32eefdea, 0x26c0b162, 0x31f79948, 0x27fdb2a7
DCD 0x30f8801f, 0x29348937, 0x2ff1d9c7, 0x2a650525
DCD 0x2ee3cebe, 0x2b8ef77d, 0x2dce88aa, 0x2cb2324c7.6 Endian Reversal and Bit Operations
本部分介绍了用于操作寄存器内位的优化算法。第7.6.1节介绍了端序反转,这是在小端内存系统中从大端文件读取数据时非常有用的操作。第7.6.2节介绍了在一个字中对位进行置换,例如,翻转位。我们展示了如何支持各种位置换。另请参阅第6.7节,了解有关打包和拆包位流的讨论。
7.6.1 Endian Reversal
//端序反转
为了最大限度地利用ARM核心的32位数据总线,您可能希望一次性以四个字节的方式加载和存储8位和16位数组。然而,如果一次性加载多个字节,则处理器的端序会影响它们在寄存器中出现的顺序。如果这与您所期望的顺序不符,则需要反转字节顺序。
您可以使用以下代码片段来反转一个字内的字节顺序。第一个代码片段使用两个临时寄存器,在常数设置周期之后,每个反转的字需要三个周期。第二个代码片段只使用一个临时寄存器,适用于反转一个单独的字。
n RN 0 ; input, output words
t RN 1 ; scratch 1
m RN 2 ; scratch 2
byte_reverse
;n=[ a, b, c, d ]
MVN m, #0x0000FF00 ; m = [0xFF,0xFF,0x00,0xFF ]
EOR t, n, n, ROR #16 ; t = [ a∧c, b∧d, a∧c, b∧d ]
AND t, m, t, LSR#8
;t=[ 0,a∧c, 0 , a∧c ]
EOR n, t, n, ROR #8 ; n = [ d , c , b , a ]
MOV pc, lr
byte_reverse_2reg
; n = [ a , b , c, d ]
EOR t, n, n, ROR#16
;t=[a∧c, b∧d, a∧c, b∧d ]
MOV t, t, LSR#8
;t=[ 0,a∧c, b∧d, a∧c ]
BIC t, t, #0xFF00
;t=[ 0,a∧c, 0 , a∧c ]
EOR n, t, n, ROR #8 ; n = [ d , c , b , a ]
MOV pc, lrARM桶移位器提供了在一个字内反转半字的功能,因为它与向右旋转16位相同,所以是免费提供的。
7.6.2 Bit Permutations

在第7.6.1节中的字节反转是位置换的一种特殊情况。还有许多其他重要的位置换,您可能会遇到(请参见表7.3):
- 字节反转
- 位反转:交换位k和31-k的值。
- 位扩展:将位间隔开,使得对于k < 16,位k移动到位2k,对于k ≥ 16,位2k - 31。
- DES初始置换:DES代表数据加密标准,它是一种常用的大规模数据加密算法。该算法在加密轮之前和之后对数据应用64位的置换。

编写实现这种置换的优化代码很简单,当您手头上有一个位置换原语的工具箱时,就像我们将在本节中开发的工具箱一样(见表7.4)。它们比逐个检查每个位的循环要快得多,因为它们一次处理32位。
让我们从符号表示开始。假设我们处理一个2k位的值n,并且我们想要对n的位进行置换。那么我们可以使用一个k位索引bk−12k−1 +···+ b12 + b0来表示n中的每个位位置。因此,对于在32位值内部置换位,我们取k = 5。
我们将研究将位于位置bk−12k−1 +···+ b12 + b0的位移动到位置ck−12k−1 +···+ c12 + c0的置换,其中每个ci都是bj或1 − bj。我们用下面的符号表示这种置换:
[bk−1, ... , b1, b0]→[ck−1, ... ,c1,c0] (7.55)
例如,Table 7.3显示了我们迄今为止讨论的置换的符号表示和操作。
这样做的目的是什么呢?实际上,我们可以使用表7.4中的三个基本置换序列来实现任何这些置换。事实上,我们只需要前两个,因为C等于B紧接着A两次。然而,我们可以直接实现C以获得更快的结果。
7.6.2.1 Bit Permutation Macros
以下宏实现了对32位字n的三个置换原语。如果常量值已经在寄存器中设置好,每个置换只需要四个周期。对于更大或更小的宽度置换,相同的思想也适用。
mask0 EQU 0x55555555 ; set bit positions with b0=0
mask1 EQU 0x33333333 ; set bit positions with b1=0
mask2 EQU 0x0F0F0F0F ; set bit positions with b2=0
mask3 EQU 0x00FF00FF ; set bit positions with b3=0
mask4 EQU 0x0000FFFF ; set bit positions with b4=0
MACRO
PERMUTE_A $k
; [ ... b_k ... ]->[ ... 1-b_k ... ]
IF $k=4
MOV n, n, ROR#16
ELSE
LDR m, =mask$k
AND t, m, n, LSR#(1 << $k) ; get bits with index b_k=1
AND n, n, m
; get bits with index b_k=0
ORR n, t, n, LSL#(1 << $k) ; swap them over
ENDIF
MEND
MACRO
PERMUTE_B $j, $k
; [ .. b_j .. b_k .. ] -> [ .. b_k .. b_j .. ] and j>k
LDR m, =(mask$j:AND::NOT:mask$k) ; set when b_j=0 b_k=1
EOR t, n, n, LSR#(1 << $j)-(1 << $k)
AND t, t, m
; get bits where b_j!=b_k
EOR n, n, t, LSL#(1 << $j)-(1 << $k) ; change if bj=1 bk=0
EOR n, n, t
; change when b_j=0 b_k=1
MEND
MACRO
PERMUTE_C $j, $k
; [ .. b_j .. b_k .. ] -> [ .. 1-b_k .. 1-b_j .. ] and j>k
LDR m, =(mask$j:AND:mask$k) ; set when b_j=0 b_k=0
EOR t, n, n, LSR#(1 << $j)+(1 << $k)
AND t, t, m
; get bits where b_j==b_k
EOR n, n, t, LSL#(1 << $j)+(1 << $k) ; change if bj=1 bk=1
EOR n, n, t
; change when b_j=0 b_k=0
MEND7.6.2.2 Bit Permutation Examples
现在,让我们看看这些宏如何在实践中帮助我们。位反转将位置b上的位移动到位置31-b上;换句话说,它会逐个取反五位索引b的每个位。我们可以使用五个A类型的变换来实现位反转,逻辑上依次取反每个位索引位置。
bit_reverse
; n= [ b4 b3 b2 b1 b0 ]
PERMUTE_A 0 ; -> [ b4 b3 b2 b1 1-b0 ]
PERMUTE_A 1 ; -> [ b4 b3 b2 1-b1 1-b0 ]
PERMUTE_A 2 ; -> [ b4 b3 1-b2 1-b1 1-b0 ]
PERMUTE_A 3 ; -> [ b4 1-b3 1-b2 1-b1 1-b0 ]
PERMUTE_A 4 ; -> [ 1-b4 1-b3 1-b2 1-b1 1-b0 ]
MOV pc, lr我们可以使用四个B类型的变换来实现更复杂的位扩展置换。这只需要16个周期(忽略常量设置),比逐个测试每个位的循环要快得多。
bit_spread
; n= [ b4 b3 b2 b1 b0 ]
PERMUTE_B 4,3 ; -> [ b3 b4 b2 b1 b0 ]
PERMUTE_B 3,2 ; -> [ b3 b2 b4 b1 b0 ]
PERMUTE_B 2,1 ; -> [ b3 b2 b1 b4 b0 ]
PERMUTE_B 1,0 ; -> [ b3 b2 b1 b0 b4 ]
MOV pc, lr最后,C类型的置换允许我们同时进行位反转和位扩展,而且使用相同数量的周期。
bit_rev_spread
; n= [ b4 b3 b2 b1 b0 ]
PERMUTE_C 4,3 ; -> [ 1-b3 1-b4 b2 b1 b0 ]
PERMUTE_C 3,2 ; -> [ 1-b3 1-b2 b4 b1 b0 ]
PERMUTE_C 2,1 ; -> [ 1-b3 1-b2 1-b1 1-b4 b0 ]
PERMUTE_C 1,0 ; -> [ 1-b3 1-b2 1-b1 1-b0 b4 ]
MOV pc, lr7.6.3 Bit Population Count
位计数(bit population count)用于统计一个字中设置为1的位数。例如,如果您需要找到中断屏蔽寄存器中设置为1的中断数量,位计数就非常有用。逐个测试每个位的循环速度较慢,因为可以使用ADD指令并行地对位进行求和,前提是求和操作不会相互干扰。"除以三再征服"的方法是将32位的字分割成位三元组。每个位三元组的和是一个范围在0到3的2位数字。我们并行计算这些和,然后以对数方式求和。使用以下代码进行单个字的位计数。该操作需要10个周期,并加上2个周期用于常量设置。
bit_count
; input n = xyzxyzxyzxyzxyzxyzxyzxyzxyzxyzxy
LDR m, =0x49249249 ; 01001001001001001001001001001001
AND t, n, m, LSL #1 ; x00x00x00x00x00x00x00x00x00x00x0
SUB n, n, t, LSR #1 ; uuzuuzuuzuuzuuzuuzuuzuuzuuzuuzuu
AND t, n, m, LSR #1 ; 00z00z00z00z00z00z00z00z00z00z00
ADD n, n, t ; vv0vv0vv0vv0vv0vv0vv0vv0vv0vv0vv
; triplets summed, uu=x+y, vv=x+y+z
LDR m, =0xC71C71C7 ; 11000111000111000111000111000111
ADD n, n, n, LSR #3 ; ww0vvwww0vvwww0vvwww0vvwww0vvwww
AND n, n, m ; ww000www000www000www000www000www
; each www is the sum of six adjacent bits
ADD n, n, n, LSR #6 ; sum the w’s
ADD n, n, n, LSR #12
ADD n, n, n, LSR #24
AND n, n, #63 ; mask out irrelevant bits
MOV pc, lr7.7 Saturated and Rounded Arithmetic
饱和操作可以将结果剪裁到一个固定的范围内,以防止溢出。您最有可能需要16位和32位的饱和操作,其定义如下:
■ 饱和16(x) = x 剪裁到范围 -0x00008000 到 +0x00007fff(包括两端)
■ 饱和32(x) = x 剪裁到范围 -0x80000000 到 +0x7fffffff(包括两端)
尽管您可以将16位饱和示例转换为8位饱和或任何其他长度,但我们将集中讨论这些操作。以下各节给出了您可能需要的基本饱和和舍入操作的标准实现。它们使用了一个标准技巧:对于一个32位有符号整数x,x >> 31 = sign(x) = -1(如果x < 0)和0(如果x ≥ 0)。
7.7.1 Saturating 32 Bits to 16 Bits
这个操作在DSP应用中经常出现。例如,声音采样通常在存储到内存之前被饱和到16位。这个操作需要3个周期,前提是一个常量m在寄存器中事先设置好。
; b=saturate16(b)
LDR m, =0x00007FFF ; m = 0x7FFF maximum +ve
MOV a, b, ASR#15
; a = (b >> 15)
TEQ a, b, ASR#31 ; if (a!=sign(b))
EORNE b, m, b, ASR#31 ; b = 0x7FFF ∧ sign(b)7.7.2 Saturated Left Shift
在信号处理中,可能会导致溢出的左移操作需要对结果进行饱和处理。这个操作对于一个常量的位移需要三个周期,对于一个变量位移c则需要五个周期。
; a=saturate32(b << c)
MOV m, #0x7FFFFFFF ; m = 0x7FFFFFFF max +ve
MOV a, b, LSL c ; a = b << c
TEQ b, a, ASR c ; if (b != (a >> c))
EORNE a, m, b, ASR#31 ; a = 0x7FFFFFFF∧sign(b)7.7.3 Rounded Right Shift
一个舍入右移操作对于一个常量的位移需要两个周期,对于一个非零的变量位移需要三个周期。请注意,如果进位标志清除,零变量位移才能正常工作。
; a=round(b >> c)
MOVS a, b, ASR c
; a = b >> c, carry=b bit c-1
ADC a, a, #0 ; if (carry) a++ to round7.7.4 Saturated 32-Bit Addition and Subtraction
在ARMv5TE核心上,新的指令QADD和QSUB提供了饱和加法和减法。如果您使用的是ARMv4T或更早版本的核心,则可以使用以下代码序列替代。该代码需要两个周期和一个保持常量的寄存器。
; a = saturate32(b+c)
MOV m, #0x80000000 ; m = 0x80000000 max -ve
ADDS a, b, c
; a = b+c, V records overflow
EORVS a, m, a, ASR#31 ; if (V) a=0x80000000∧sign(a)
; a = saturate32(b-c)
MOV m, #0x80000000 ; m = 0x80000000 max -ve
SUBS a, b, c
; a = b-c, V records overflow
EORVS a, m, a, ASR#31 ; if (V) a=0x80000000∧sign(a)7.7.5 Saturated Absolute
如果输入参数是 -0x80000000,绝对值函数会发生溢出。以下的两个周期的代码序列处理了这种情况:
; a = saturate32(abs(b))
SUB a, b, b, LSR #31 ; a = b - (b<0)
EOR a, a, a, ASR #31 ; a = a ∧ sign(a)在类似的情况下,一个累积的、非饱和的绝对值函数也需要两个周期:
; a = b+abs(c)
EORS a, c, c, ASR#32
;a=c∧sign(c) = abs(c)-(c<0)
ADC a, b, a
;a=b+a+ (c<0)7.8 Random Number Generation
要生成真正的随机数,需要特殊的硬件作为随机噪声的来源。然而,对于许多计算机应用程序(如游戏和建模),生成速度比统计纯度更为重要。这些应用程序通常使用伪随机数。
伪随机数实际上并不是真正的随机数;它们是由一个重复的序列生成的数字。然而,该序列非常长,并且分散得很广,使得这些数字看起来是随机的。通常,我们通过迭代一个关于 Rk−1 的简单函数来获取伪随机序列的第 k 个元素 Rk:
![]()
为了获得快速的伪随机数生成器,我们需要选择一个容易计算并且输出看起来随机的函数 f(x)。在重复之前,序列必须非常长。对于一个32位数字的序列而言,最长的长度显然是 2^32。
线性同余生成器使用以下形式的函数:
f(x) = (a*x+c) % m;
这些函数在《Knuth, Seminumerical Algorithms》的3.2.1节和3.6节中有详细研究。为了进行快速计算,我们希望取 m = 2^32。《Knuth》中的理论保证,如果 a%8 = 5 并且 c = a,则生成的序列具有 2^32 的最大长度,并且很可能看起来是随机的。例如,假设 a = 0x91e6d6a5。那么下面的迭代将生成一个伪随机序列:
MLA r, a, r, a ; r_k = (a*r_(k-1) + a) mod 2^32
由于 m 是2的幂,序列的低位并不是很随机。使用高位来生成较小范围内的伪随机数。例如,设置 s = r << 28 来生成一个范围在0到15之间的四位随机数 s。更一般地,以下代码可以生成一个介于0和n之间的伪随机数:
; r is the current random seed
; a is the multiplier (eg 0x91E6D6A5)
; n is the random number range (0...n-1)
; t is a scratch register
MLA r, a, r, a ; iterate random number generator
UMULL t, s, r, n ; s = (r*n)/2∧32
; r is the new random seed
; s is the random result in range 0 ... n-17.9 Summary
ARM指令只实现了简单的基本操作,如加、减和乘法。要执行更复杂的操作,如除法、平方根和三角函数,需要使用软件例程。有许多有用的技巧和算法来提高这些复杂操作的性能。本章介绍了一些标准操作的算法和代码示例。
标准技巧包括:
■ 使用二分查找或试减法计算小商
■ 使用牛顿-拉夫逊迭代快速计算倒数和提取根号
■ 使用表查找和级数展开的组合来计算超越函数,如exp,log,sin和cos
■ 使用带有桶位移动的逻辑操作执行比逐个测试位更高效的位置换
■ 使用乘积累加指令生成伪随机数
)

安装nfs服务器)
的应用——图像处理篇)






)
)





)

