暑期算法训练.9

43 .力扣75 颜色分类

43.1 题目解析：

43.2 算法思路：

43.3 代码演示：

43.4 总结反思：

44. 力扣 912 排序数组

44.1 题目解析：

44.2 算法思路：

44.3 代码演示：

编辑

44.4 总结反思：

45. 力扣215 数组中第k个最大的元素

45.1 题目解析：

45.2 算法思路：

编辑

45.3 代码演示：

45.4 总结反思

46. 剑指offer 40.最小的k

46.1 题目解析：

46.2 算法思路：

46.3 代码演示：

编辑

46.4 总结反思

43 .力扣75 颜色分类

43.1 题目解析：

咱们今天讲的题目都是涉及到一个算法，就是分治算法，即分而治之。顾名思义，就是把一个大问题分成很多个小问题，一直分，直到那个小问题可以被解决为止。之后再回溯，这个时候，那个大问题，也基本就被解决了.......以此类推即可

这道题目很好理解，就是排序，但是不可以使用sort函数，所以就增加了一点难度。

43.2 算法思路：

本题咱们可以使用三指针来做。那么咱们之前学过双指针对吧。

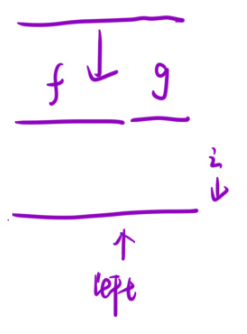
遍历i，从左往右进行遍历，之后判断left，最终left要停在结束的位置即可。把整个数组分成了2份。

好，那么类比一下，咱们可以推出三指针：

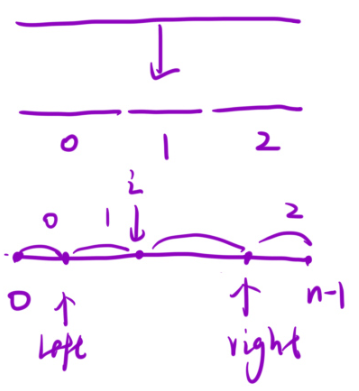
其实最后是把整个数组分成了四部分：

i：遍历数组

left：标记0区域的最右侧

right：标记2区域的最左侧

那么[0,left]才全为0，那么得从left+1开始才是1的区域（因为在数组中，是一个一个的数。因为这个数在0区间内，那么下一个数只能在1区间内）直到i-1。（因为i这个位置还没有扫描呢，还没有判断，所以说，只可以到i-1）。之后i到right-1为扫描元素，后面的[right,n-1]才全都是2.

之所以这么算，是因为：

left与right都是从数组之外开始的。

那么，咱们先来看总结的规律：

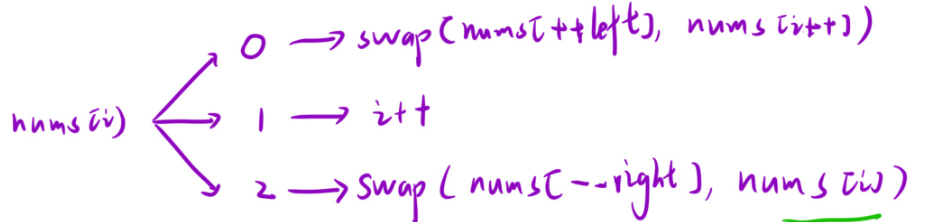
1.nums[i]：为0的时候，0应该是在left这个区间内的，得让nums[i]与nums[left+1]交换，为什么与left+1 交换呢？因为咱们的left，right这俩个指针也得动啊，那你0换到left+1，left再加加，不就正好[0,left]为0了嘛？之后i再加加，因为此时[left+1,i-1]，此时i++完了，那么i-1才是刚才交换后1的位置（i从左往右挪动到这的时候，差不多可以这么挪动了，之前left+1这个位置，差不多是1，就算不是也没事）。那么若1正好在left+1的地方，i正好为0.也要交换（自己交换自己）。交换之后两个都要加加。此时swap([nums[++left],nums[i++]),既然都要写left+1交换，且后面left还要加加，不如直接写++left。

2.当nums[i]恰好为1的时候，直接i++即可。因为i-1的位置得为1.

3.若nums[i]为2，那么swap(nums[--right],nums[i])，因为right的位置为2，且right后面还得减减，所以得让right-1位置与i交换，之后right--。但是没交换之前right-1位置为未扫描，交换后i位置还是未扫描，所以i不用移动！

且直到循环到i==right的时候，因为此时待扫描的区间已经没有了。循环也就停止了。即while(i<right)

好了，本题的算法终于分析完了。本题的算法对于后面的题目也有用处，所以大家要好好的研读一下。

43.3 代码演示：

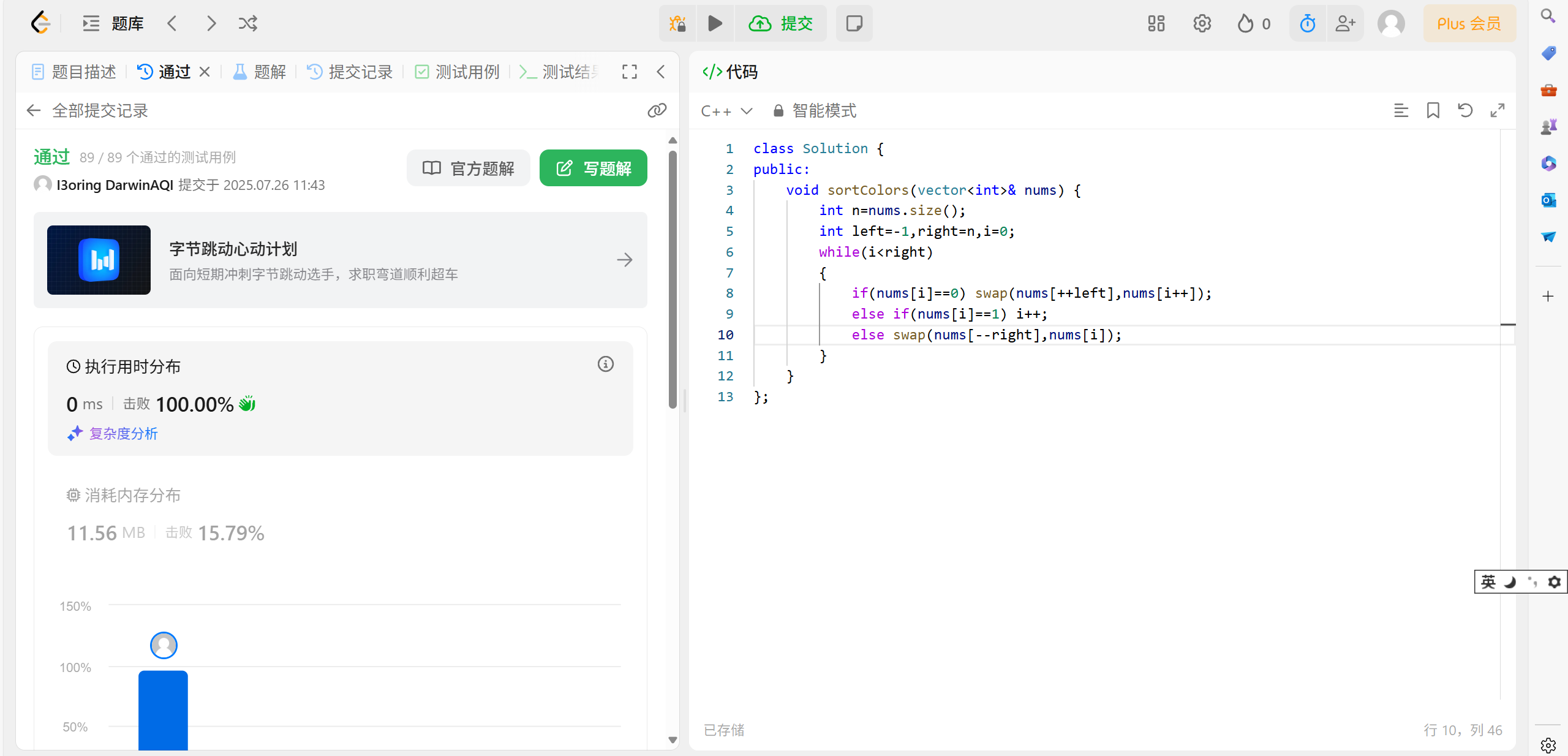
void sortColors(vector<int>& nums) {int n = nums.size();int left = -1, right = n, i = 0;while (i < right){if (nums[i] == 0) swap(nums[++left], nums[i++]);else if (nums[i] == 1) i++;else swap(nums[--right], nums[i]);}
}
int main()
{vector<int> nums = { 2,0,1,0,2,1 };sortColors(nums);for (auto& e : nums){cout << e << "";}cout << endl;return 0;
}

43.4 总结反思：

代码量其实还是挺少的，只要还是看这个思路一定要掌握。

44. 力扣 912 排序数组

44.1 题目解析：

题目很好理解，就是让你排序。

44.2 算法思路：

咱们这道题目采用的是快速排序，那么之前咱们一定学过将数组分成两份的那种快速排序。那种也可以解决这种问题。

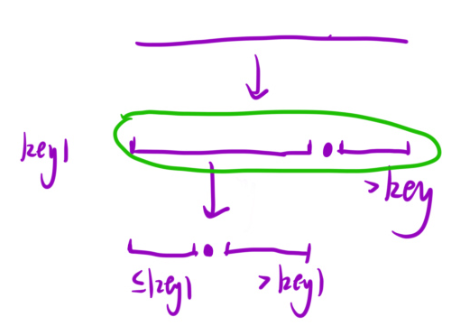
但是呢，当所有的元素有一样的时候，这个时候，这个key就会跑到最右侧。那么下次分的时候，还是分这个一大块。所以时间复杂度就是O（n^2)，挺不好。

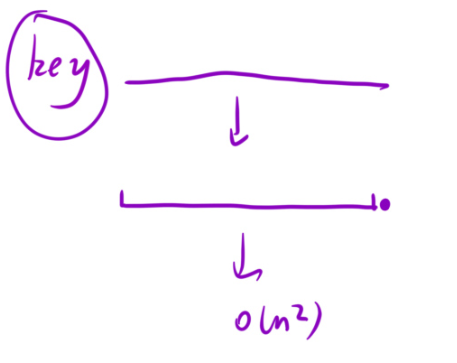
所以，咱们今天将使用数组分三块来实现快速排序（key将数组分成了三块）

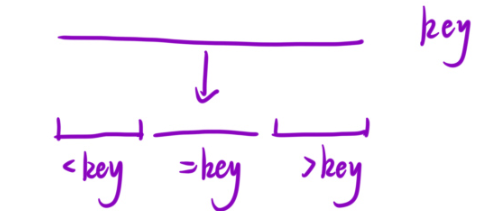
最后等于key的这个部分就不需要再管了，只需要对小于key的，以及大于key的再进行递归就可以了。

最后还是

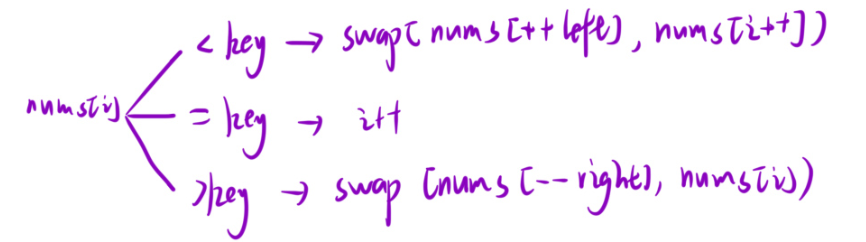还是这些，所以搞懂上一题的算法很有必要。

那么为什么说数组分三块的效率更高呢？因为当元素都一样的时候，由于咱们只需要对小于key以及大于key的进行递归，但是元素都一样了，根本不需要递归了。所以分一次就可以停止了。时间复杂度就是O（n）,肯定快。

2.优化：使用随机的方式选择基准值

快排时复杂度要想靠近N*logN,必须得使用随机方式选基准值，因为只有这种方式才是等概率的。证明方法大家可以去《算法导论》这本书上找。

注意，上面的，这个left+r%(right-left+1)仅仅只是下标，咱们还得在外面套上nums才可以。

别忘了还得种下一个随机数种子：srand(time(NULL))

44.3 代码演示：

// 先声明 Random 和 qsortl。因为程序是从上到下执行的，所以说你要是不提前声明存在这两个函数的话，编译器是找不到的，当然，你在做力扣的题目的时候，是不需要写的
int Random(vector<int>& nums, int left, int right);
void qsortl(vector<int>& nums, int l, int r);vector<int> sortArray(vector<int>& nums) {srand(time(NULL));//种下一颗随机数种子qsortl(nums, 0, nums.size() - 1);//这个其实就是给后面要实现的qsort函数进行传参return nums;}void qsortl(vector<int>& nums, int l, int r)//这个是区间的左端点与区间的右段点，这个l其实就是0，r就是nums.size()-1（这个只是最初始的是0跟nums.size()-1，后面的就跟递归有关了{if (l >= r) return;//说明此时只有一个元素，或者是区间不存在，直接返回即可int key = Random(nums, l, r);int i = l, left = l - 1, right = r + 1;//这个地方涉及到递归，所以i是遍历的l到r，但是递归的时候，l与r不是每次都是一样的数值，所以，i得赋值为l(这个不是数字1)while (i < right){if (nums[i] < key) swap(nums[++left], nums[i++]);else if (nums[i] == key) i++;else swap(nums[--right], nums[i]);}//递归//[l,left][left+1,right-1][right,r]qsortl(nums, l, left);qsortl(nums, right, r);}int Random(vector<int>& nums, int left, int right)//这个时候才是对第一次定义的qsort中的left，right的应用{int r = rand();return nums[r % (right - left + 1) + left];}int main()
{vector<int> nums = { 5,2,3,1 };vector<int> outcome = sortArray(nums);for (auto& e : outcome){cout << e << "";}cout << endl;return 0;
}

这道题目开始，i就是l（不是1），不是0了。因为i的作用就是遍历区间，虽然说第一次的区间是0到n-1，但是还有递归啊，递归后的这个i就不能再是0了。所以直接让i随着l变化就可以了

代码确实挺长的，但是大家只要理解了思路，就挺简单的。

44.4 总结反思：

其实这道题目还是运用了数组分三块加上随机产生基准值。大家以后写快速排序的时候，也可以这么写，这么写是比数组分两块来进行写，写的快的。

45. 力扣215 数组中第k个最大的元素

45.1 题目解析：

本题就是典型的topk问题，topk问题的问法有很多，比如1.找第k大 2.找第k小 3.前k大 4.前k小

通常可以使用堆排序（时复为O（n*logn）），以及今天介绍的快速选择算法：（时复为O（n））。这里的快速选择算法，只需要去一个区间寻找就可以了。

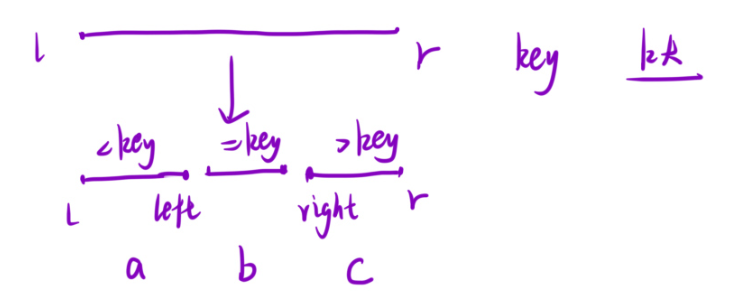
45.2 算法思路：

a，b，c代表的是区间的元素的个数。

那么1.若c>=k,则第k个大的元素会落在[right,r]这个区间内，去这儿找第k个大的元素（后面还得继续在这个区间内qsort，代码中有的，记得看代码）

2.第二种情况，说明第一种情况一定不成立：b+c>=k,因为c>=k不成立（c<k),所以第k大个元素，一定在b这个区间内，则直接返回key。

3.则第一种与第二种情况一定不成立。所以去[l,left]内寻找，不就是找第k-b-c个大的元素嘛？

所以快速选择就是根据数量划分去某一个区间找。

这里需要算一个区间的长度：咱们直到左闭右闭的区间长度是right-left+1，所以c的区间长度是r-right+1.但是b的区间长度right-1-（left+1）+1，就是right-left-1.

45.3 代码演示：

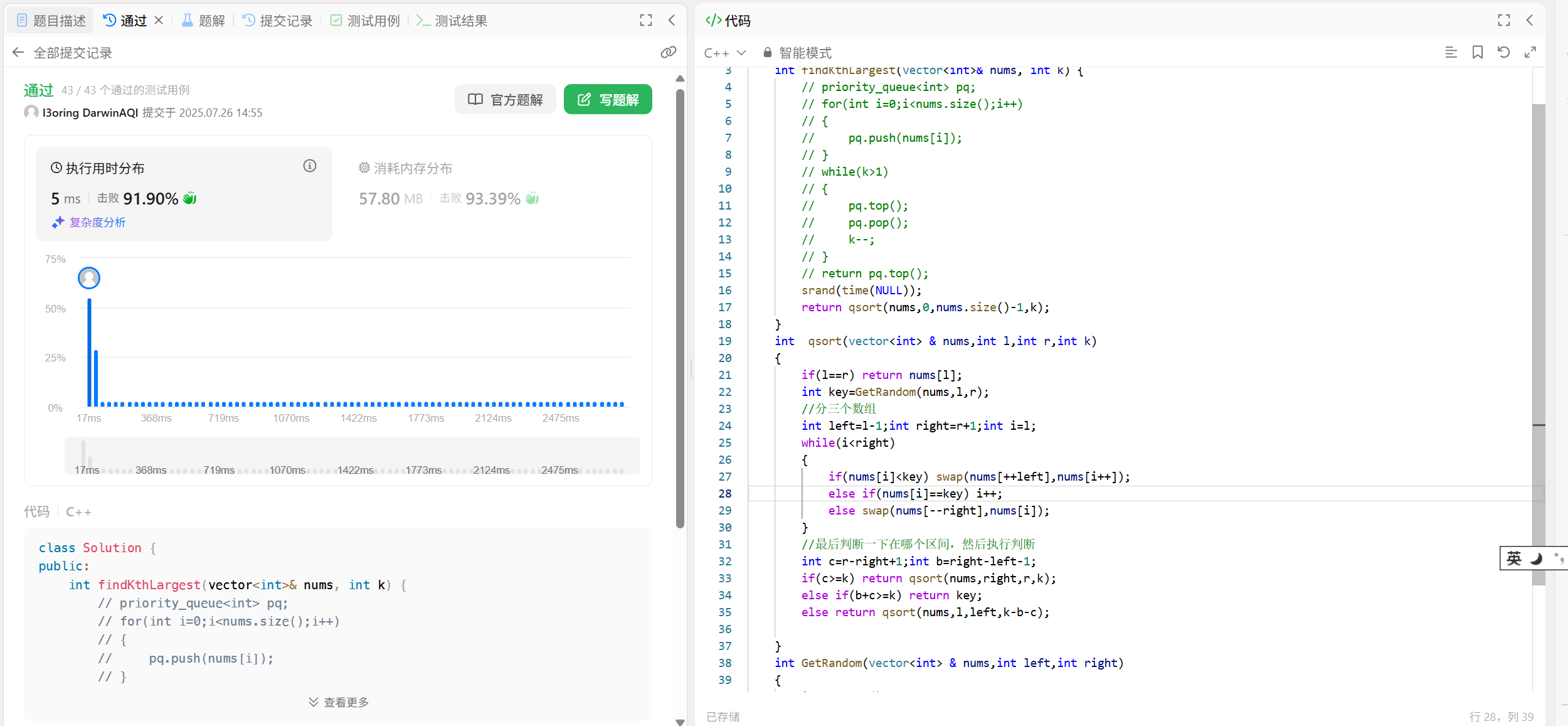
int  qsort2(vector<int>& nums, int l, int r, int k);
int GetRandom(vector<int>& nums, int left, int right);int findKthLargest(vector<int>& nums, int k) {srand(time(NULL));return qsort2(nums, 0, nums.size() - 1, k);
}
int  qsort2(vector<int>& nums, int l, int r, int k)
{if (l == r) return nums[l];//若数组中只有一个元素，这个只要是进入了qsort这个函数，则数组区间一定存在int key = GetRandom(nums, l, r);//分三个数组int left = l - 1; int right = r + 1; int i = l;while (i < right){if (nums[i] < key) swap(nums[++left], nums[i++]);else if (nums[i] == key) i++;else swap(nums[--right], nums[i]);}//最后判断一下在哪个区间，然后执行判断int c = r - right + 1; int b = right - left - 1;if (c >= k) return qsort2(nums, right, r, k);else if (b + c >= k) return key;else return qsort2(nums, l, left, k - b - c);//这里别忘了return}
int GetRandom(vector<int>& nums, int left, int right)
{int r = rand();return nums[r % (right - left + 1) + left];
}
int main()
{vector<int> nums = { 3,2,1,5,6,4 };int k = 2;cout << findKthLargest(nums, k) << endl;return 0;
}

哇，这个的代码量也是挺多的。

45.4 总结反思

这里涉及到了几个问题，我会在最后一个问题全部说清楚。

46. 剑指offer 40.最小的k

46.1 题目解析：

这道题目也是属于topk问题，只不过是寻找一个范围k。

46.2 算法思路：

解法一：可以使用排序方法，然后找出前k个小的元素即可（时间复杂度为O（n*logn））

解法二：利用堆排序（找最小的，用大根堆）（时间复杂度为O（n*logk））。

解法三就是使用快速选择算法了：（时间复杂度为O（n））

依旧是数组分三块加上随机选择基准值

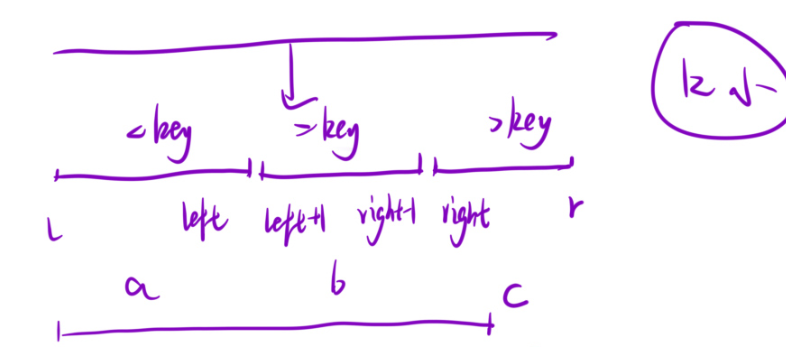
1.若a>k,前k小在a里面，去[l,left]中寻找最小的k个元素。

2.a+b>=k,此时第一种情况一定不成立，那么k>=a,又因为b区间内都是相同的元素，所以此时可以直接返回了。因为b内元素都是相同的，不需要再去找前k-a个小的了。

3.若第一种与第二种情况都不成立。那么就去[right,r]内去找最小的k-a-b个元素即可。

这里快就快在，他没有排序（这个里面只是小于基准值，大于基准值，可能小于基准值里面的顺序不是排好的）。所以它管你是小于还是大于，直接找到前k个小的元素即可。

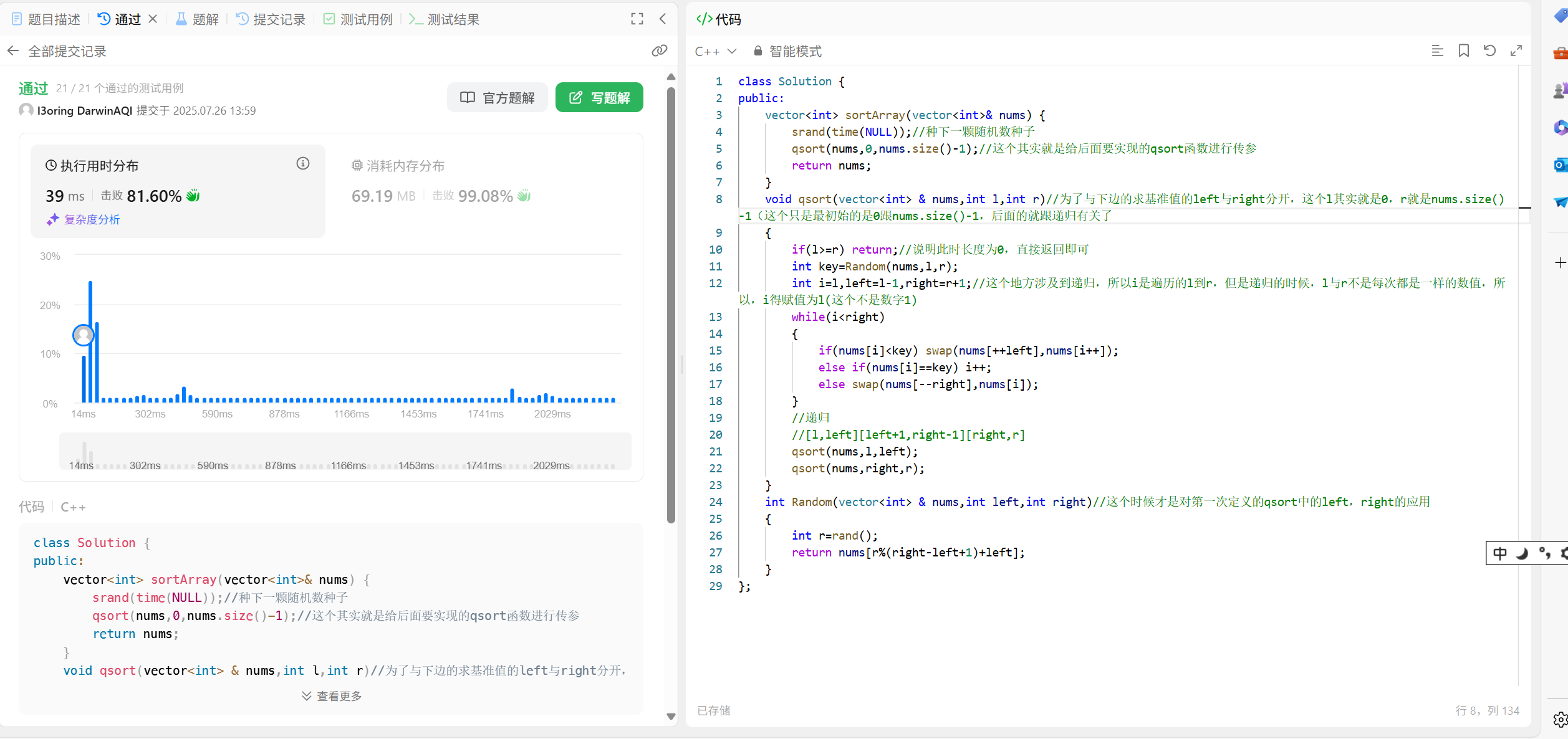
46.3 代码演示：

void qsort(vector<int>& nums, int l, int r, int k);
int getRandom(vector<int>& nums, int l, int r);vector<int> getLeastNumbers(vector<int>& nums, int k)
{srand(time(NULL));qsort(nums, 0, nums.size() - 1, k);return { nums.begin(), nums.begin() + k };
}
void qsort(vector<int>& nums, int l, int r, int k)
{if (l == r) return;// 1. 随机选择⼀个基准元素+数组分三块int key = getRandom(nums, l, r);int left = l - 1, right = r + 1, i = l;while (i < right){if (nums[i] < key) swap(nums[++left], nums[i++]);else if (nums[i] == key) i++;else swap(nums[--right], nums[i]);}// [l, left][left + 1, right - 1] [right, r]// 2. 分情况讨论int a = left - l + 1, b = right - left - 1;if (a > k) qsort(nums, l, left, k);else if (a + b >= k) return ;//直接return是因为最上面已经有return了， return { nums.begin(), nums.begin() + k };//且这个是void返回值else qsort(nums, right, r, k - a - b);
}
int getRandom(vector<int>& nums, int l, int r)
{return nums[rand() % (r - l + 1) + l];
}
int main()
{vector<int> nums = { 2,5,7,4 };int k =1 ;vector<int> outcome = getLeastNumbers(nums, k);for (auto& e : outcome){cout << e << "";}cout << endl;return 0;
}

好，咱们看44题里面是l>=r,而第45，46题里面都是l==r，为什么呢？

那么咱们要先知道，为什么排序的时候会有>=?

关键点

快速排序（Quicksort） 的目标是 完全排序数组，需要处理所有子区间。

分区逻辑 不同：

分区后递归 [l, left] 和 [right, r]。

可能出现 空区间：

如果所有元素 ≤ key，则 left 可能等于 r，导致 [right, r] 为空。

如果所有元素 ≥ key，则 right 可能等于 l，导致 [l, left] 为空。

为什么需要 l >= r？

快速排序的递归调用 不保证区间非空：

可能递归到 [l, left] 时 left < l（区间无效）。

需要 if (l >= r) 提前终止无效递归。

示例

假设 nums = [1, 1, 1]：

分区后 key = 1，left = -1，right = 3。

递归 [0, -1]（无效）和 [3, 2]（无效）。

需要 if (l >= r) 避免无限递归。

主要就是解决这个无效的区间的问题。

那么为什么后面两个不需要大于呢？因为后面两个快速选择算法，假如，都是元素相同的数组，那么[right,r]是无效的区间对吧，但是第一次调用qsort的时候就已经返回了，它不会进入递归，知道吧，所第二次并不会出现[right,r]这个区间，那么排序就不同了，排序是不管怎样，都要递归，所以说，排序算法才需要>=,就是为了处理递归的时候的无效区间。

等于的时候是，数组中只有一个元素的时候。

还有一个问题就是：会发现，当返回的是数组的时候，直接return就可以了。那是因为前面已经有了return。