给你一个无向图,无向图由整数 n ,表示图中节点的数目,和 edges 组成,其中 edges[i] = [ui, vi] 表示 ui 和 vi 之间有一条无向边。同时给你一个代表查询的整数数组 queries 。
第 j 个查询的答案是满足如下条件的点对 (a, b) 的数目:
a < b
cnt 是与 a 或者 b 相连的边的数目,且 cnt 严格大于 queries[j] 。
请你返回一个数组 answers ,其中 answers.length == queries.length 且 answers[j] 是第 j 个查询的答案。
请注意,图中可能会有 多重边 。
示例 1:
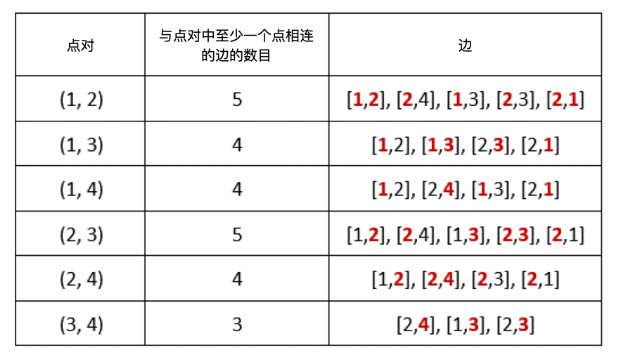
输入:n = 4, edges = [[1,2],[2,4],[1,3],[2,3],[2,1]], queries = [2,3]
输出:[6,5]
解释:每个点对中,与至少一个点相连的边的数目如上图所示。
answers[0] = 6。所有的点对(a, b)中边数和都大于2,故有6个;
answers[1] = 5。所有的点对(a, b)中除了(3,4)边数等于3,其它点对边数和都大于3,故有5个。
示例 2:
输入:n = 5, edges = [[1,5],[1,5],[3,4],[2,5],[1,3],[5,1],[2,3],[2,5]], queries = [1,2,3,4,5]
输出:[10,10,9,8,6]
提示:
2 <= n <= 2 * 104^44
1 <= edges.length <= 105^55
1 <= ui, vi <= n
ui != vi
1 <= queries.length <= 20
0 <= queries[j] < edges.length
法一:我们可以先把每个点的度计算出来,然后对于一个查询,它要求连接两点之一的边数大于一个值q,我们就可以把每个点的度排序,然后相向双指针计算出两点度之和大于q的点对数,但这样计算可能会多算重复值,比如示例1中的边12和边21,这两条边计算出来点1和点2的度都是2,两者相加就是4,但其实只有2条边,我们需要用两个点的度4减去相同的边的数量2,如果减少2后的值小于等于q,则答案需要减去1对点对:
class Solution {
public:vector<int> countPairs(int n, vector<vector<int>>& edges, vector<int>& queries) {// 保存每个点的度vector<int> deg(n + 1);// 保存两点间的边数unordered_map<int, int> cntEdge;for (vector<int> &edge : edges) {int x = edge[0];int y = edge[1];++deg[x];++deg[y];if (x > y) {swap(x, y);}// 可以用一个int保存两个值小于等于65535的数// 这里表示从x到y的边数增加1++cntEdge[x << 16 | y];}vector<int> sortedDeg = deg;sort(sortedDeg.begin(), sortedDeg.end());vector<int> ans(queries.size());for (int i = 0; i < queries.size(); ++i) {int left = 1;int right = n;while (left < right) {if (sortedDeg[left] + sortedDeg[right] > queries[i]) {ans[i] += right - left;--right;} else {++left;}}for (auto [k, c] : cntEdge) {int x = k >> 16;int y = k & 0xffff;// 如果点x和点y的度之和大于查询目标值,说明该点对计入了答案// 如果减去相同的边数后不大于查询目标值了,说明该点对不应计入答案if (deg[x] + deg[y] > queries[i] && deg[x] + deg[y] - c <= queries[i]) {--ans[i];}}}return ans;}
};
如果edges的长度为m,queries的长度为q,则此算法时间复杂度为O(nlogn + q(n + m)),空间复杂度为O(n+m),cntEdge的长度最多为m。
法二:我们可以构建一个数组,该数组的key为与点对相连的边的数量,value为有多少个点对相连的边的数量为key,这样对于某个查询q,答案就是数组下标大于q的所有元素和,即用后缀和来获得答案:
class Solution {
public:vector<int> countPairs(int n, vector<vector<int>>& edges, vector<int>& queries) {// 用时O(n)vector<int> deg(n + 1);unordered_map<int, int> cntEdge;// 用时O(m)for (vector<int> &edge : edges) {int x = edge[0];int y = edge[1];++deg[x];++deg[y];if (x > y) {swap(x, y);}++cntEdge[x << 16 | y];}// key为度,value为度为key的点数unordered_map<int, int> degToNum;// 用时O(n)for (int i = 1; i < deg.size(); ++i) {++degToNum[deg[i]];}int maxDeg = *max_element(deg.begin() + 1, deg.end());int k = maxDeg * 2 + 2;// key为与点对相连的边的数量,value为点对相连的边数为key的点对数量vector<int> degCnt(k);// 暴力计算任意两点的度数和,并将度数和填入degCnt,计算后degCnt会包含重复边// 如果边的数量为m,这里的时间复杂度为m// 因为平均情况下假设有x种度数,则度数和为1+2+3+...+x=(1+x)x/2// 而度数和有2m个,因此x平均值为根号(4m),两重循环的平均时间就是O(m)for (auto [deg1, cnt1] : degToNum) {for (auto [deg2, cnt2] : degToNum) {// 为避免重复计算,只计算deg1<=deg2的情况// 如果是小于// 例如degToNum为[0,2,3],表示度为1的有2个点,度为2的有3个点// deg1为1,deg2为2,此时度的和为5的点对数中,deg1和deg2贡献了2*3个if (deg1 < deg2) {degCnt[deg1 + deg2] += cnt1 * cnt2;// 如果是等于// 例如度为3的点有4个,那么度的和为6的点对数中,deg1和deg2两两配对// 贡献了cnt1 * (cnt1 - 1) / 2个} else if (deg1 == deg2) {degCnt[deg1 + deg2] += (cnt1 - 1) * cnt1 / 2;}}}// 去除重复边,如果点对间有num个边,说明该点对数实际与这两点相连的边数为s-num// 即度的和为s的两点实际相连的边数为s-num// 用时最大O(m)for (auto [edge, num] : cntEdge) {int s = deg[edge >> 16] + deg[edge & 0xffff];++degCnt[s - num];--degCnt[s];}// 计算后缀和// 用时O(m),因为对于所有的点,每个点最多有m个度for (int i = k - 1; i > 0; --i) {degCnt[i - 1] += degCnt[i];}// 计算每个查询的结果,查询为q时,degCnt[q]为大于等于q的点对数// 在q只能取整数的情况下,degCnt[q+1]即为大于q的点对数// 超出索引时,查询的答案为0// 此处我们用两倍的最大度数加1表示超出索引// 上面双重循环中,degCnt中最大key就是两个最大度的和// 用时O(q)for (int &q : queries) {q = degCnt[min(q + 1, k - 1)];}return queries;}
};
此算法时间复杂度为O(n+m+q),空间复杂度为O(n+m)。









)
** 的介绍)






游记))
 部署资源的完整配置OceanBase)
)