接上篇
重温无功功率测量-CSDN博客
已知被测阻抗两端电压与流过 通过两个ADC同步采集到。
激励频率10k, 采样率1M, 每周期100个点
关键是:采样率除以激励频率, 得是4的倍数... 所以ADC不能自由运行, 得用一个timer来触发.
因为要进行同相分量正交分量计算。
1:直流分量计算
int buf_size = sizeof(pdc->data.adc_buf) / sizeof(pdc->data.adc_buf[0]);for(int i = 0; i < buf_size; i++) {mean_v += pbuf[i].v;mean_i += pbuf[i].i;}mean_v /= buf_size;mean_i /= buf_size; // 求平均值, 用于直流平衡2:计算相位
for(int i = 50; i < buf_size - 50; i++) {prod_i += -(pbuf[i].v - mean_v) * (pbuf[i].i - mean_i); // v和i做直流平衡后相乘, 累加得到同相分量prod_q += (pbuf[i + 25].v - mean_v) * (pbuf[i].i - mean_i); // 激励频率10k, 采样率1M, 每周期100个点, 因此移动25个点再平衡, 相乘, 累加就是正交分量了}prod_i /= buf_size;prod_q /= buf_size;phase = atan2(prod_q, prod_i); // 同相分量和正交分量, atan2即得到相位差原理解释
使用
atan2函数和同相、正交分量的平均值,确实可以得到相位角。 这也是一种在数字信号处理中非常常用和稳健的相位计算方法。原理简述
首先,让我们理解什么是同相分量和正交分量。
假设你有一个信号 s(t)=Acos(ωt+ϕ),它的同相分量 (In-phase, I) 和正交分量 (Quadrature, Q) 可以通过将其与参考信号(通常是 cos(ωt) 和 −sin(ωt) 或 sin(ωt))相乘,并取其在周期内的平均值来得到。
同相分量 (I): 表示信号在参考信号 cos(ωt) 上的投影。它与信号的幅度和相位有关。
正交分量 (Q): 表示信号在参考信号 sin(ωt) 上的投影。它也与信号的幅度和相位有关。
通过积分或求平均值,我们可以得到:
I=T1∫0Ts(t)cos(ωt)dt=2Acos(ϕ)
Q=T1∫0Ts(t)sin(ωt)dt=2Asin(ϕ)
注意:在数字信号处理中,积分会变成求和。
为什么
atan2(Q, I)有效?根据上面的公式,我们可以看到:
IQ=2Acos(ϕ)2Asin(ϕ)=cos(ϕ)sin(ϕ)=tan(ϕ)
所以,ϕ=arctan(IQ)。
但是,
arctan(y/x)有一个问题:它只能输出 −π/2 到 π/2 之间的角度,无法区分第一、三象限和第二、四象限的角度。
atan2(y, x)函数解决了这个问题。它通过同时使用 y (这里的 Q) 和 x (这里的 I) 的正负号信息,来确定相位角所在的完整 2π 范围,即 −π 到 π。
如果 I>0,Q>0,相位角在第一象限。
如果 I<0,Q>0,相位角在第二象限。
如果 I<0,Q<0,相位角在第三象限。
如果 I>0,Q<0,相位角在第四象限。
因此,
atan2(Q, I)能够精确地计算出信号的相位角,而不会产生象限模糊。步骤
选择基准频率:确定你要分析的信号的基波频率 f0,并生成两个正交的参考信号:cos(2πf0t) 和 sin(2πf0t)。
计算同相分量 (I):将你的原始采样信号与 cos(2πf0t) 相乘,并对结果求平均值(或在一个周期内求和)。
计算正交分量 (Q):将你的原始采样信号与 sin(2πf0t) 相乘,并对结果求平均值(或在一个周期内求和)。
计算相位角:将得到的 Q 和 I 值代入
atan2函数:相位角=atan2(Q,I)
这个方法等同于对信号进行离散傅里叶变换 (DFT),然后取基波频率处的实部和虚部。同相分量 I 对应于傅里叶变换的实部,正交分量 Q 对应于傅里叶变换的虚部。因此,这是一种非常可靠且常用的方法。
这种方法通常被称为 I/Q 解调 (In-phase and Quadrature Demodulation) 或 正交解调。
在数字信号处理中,I/Q 是同相 (In-phase) 和正交 (Quadrature) 的缩写。通过将信号分别与一对正交的参考信号(例如 cos(ωt) 和 sin(ωt))相乘并求平均,我们可以提取出信号的 I 分量和 Q 分量。
I 分量 对应于信号的实部。
Q 分量 对应于信号的虚部。
这两个分量共同构成了一个复数,这个复数包含了信号的幅度和相位信息。而
atan2(Q, I)函数正是用来从这个复数中计算出精确的相位角。因此,这个方法在很多领域都有广泛应用,尤其是在通信、雷达和各种数字信号处理系统中,用来对信号进行解调、分析和处理。
3:计算阻抗模
for(int i = 50; i < buf_size - 50; i++) {rms_sq_sum_v += pow((pbuf[i].v - mean_v),2); rms_sq_sum_i += pow((pbuf[i].i - mean_i),2);}float U_rms = sqrt(rms_sq_sum_v / buf_size);float I_rms = sqrt(rms_sq_sum_i / buf_size);float Z_modulus = U_rms / I_rms;原理解释
第1步:计算电压的有效值 (U_rms)
有效值(方均根值)代表了交流信号的等效能量。它的计算方法是:
对每个电压采样点进行平方。
将所有平方值相加求和。
将求和结果除以采样点数 (1000)。
对最终结果开方。
第2步:计算电流的有效值 (I_rms)
使用同样的方法计算电流的有效值:
对每个电流采样点进行平方。
将所有平方值相加求和。
将求和结果除以采样点数 (1000)。
对最终结果开方。
第3步:计算阻抗的模 (∣Z∣)
阻抗的模等于电压的有效值除以电流的有效值。
∣Z∣=Urms/Irms
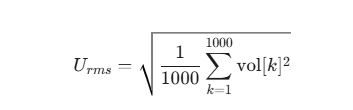
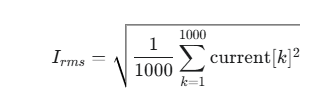



![Agents-SDK智能体开发[4]之集成MCP入门](http://pic.xiahunao.cn/Agents-SDK智能体开发[4]之集成MCP入门)















