高级项目——基于FPGA的串行FIR滤波器

给大家安利一个 AI 学习神站！在这个 AI 卷成红海的时代，甭管你是硬核开发者还是代码小白，啃透 AI 技能树都是刚需。这站牛逼之处在于：全程用 "变量名式" 幽默 + 生活化类比拆解 AI，从入门到入土（啊不，到精通）一站式通关，理解效率直接拉满。话不多说，链接甩这了→前言 – 人工智能教程

项目目标： 在FPGA上实现一个使用汉明窗设计的FIR低通滤波器，并通过仿真验证其滤波效果。

一、FIR 原理

1. FIR = 加权移动平均（升级版）： 想象在听一串连续的声音采样值（x[n], x[n-1], x[n-2], ...）。FIR 滤波器计算当前输出 y[n] 的方式是：把当前的和过去若干个输入样本，各自乘上一个特定的“权重”（系数 h[k]），然后把所有这些乘积加起来。

2. “有限”的含义： 它只使用有限个 (N+1 个) 过去的样本（x[n] 到 x[n-N]）。N+1 就是滤波器的抽头数（Taps），N 是阶数。抽头数越多，滤波器能实现的频率响应特性（比如截止陡峭度、阻带衰减）通常越好，但计算量也越大。

3. 公式： y[n] = h[0]*x[n] + h[1]*x[n-1] + h[2]*x[n-2] + ... + h[N]*x[n-N]

4. 关键点： 这些系数 h[0], h[1], ..., h[N] 决定了滤波器的特性（低通、高通、带通等）。系数不同，滤波效果就完全不同。

5. 窗函数（汉明窗）的作用： 直接计算理想滤波器的系数（无限长）不可行。窗函数（如汉明窗）像一把平滑的“剪刀”，把理想的、无限长的系数序列“截短”成我们需要的有限长 (N+1个)，同时尽量减小截短带来的不良影响（如吉布斯效应），让滤波器的实际频率响应更接近理想状态。

二、MATLAB 部分

目标： 根据想要的滤波器特性（低通，Fs（采样频率）=100kHz, Fc（截止频率）=10kHz），计算出 32 个 (N+1=32) 最优的量化系数 h_quant[0:31]。

步骤：

1. 计算归一化截止频率： Wn = Fc / (Fs/2) = 10000 / 50000 = 0.2

2. 调用 fir1 函数设置滤波器： h = fir1(31, 0.2, 'low', hamming(32));

        31： 滤波器阶数 N (抽头数 Taps = N+1 = 32)。

        0.2： 归一化截止频率 Wn。

        'low'： 低通滤波器。

        hamming(32)： 使用 32 点的汉明窗。

% 滤波器参数
Fs = 100000;   % 采样频率 (Hz)
Fc = 10000;    % 截止频率 (Hz)
N = 31;        % 滤波器阶数 (抽头数 = N + 1 = 32)
% 计算归一化截止频率 (范围 0-1, 1对应 Fs/2)
Wn = Fc / (Fs/2); % Wn = 10000 / 50000 = 0.2
% 使用 fir1 函数设计汉明窗低通FIR滤波器
% fir1(阶数, 归一化截止频率, 滤波器类型, 窗函数)
h = fir1(N, Wn, 'low', hamming(N+1)); % hamming(N+1) 生成 N+1 点的汉明窗

        同时需要检查图形，通带是否在0-10kHz相对平坦？阻带衰减是否足够（汉明窗典型约-53dB）？过渡带是否在预期位置？

% 绘制频率响应
freqz(h, 1, 1024, Fs); % freqz(系数, 分母(1表示FIR), FFT点数, 采样频率)
title('FIR Lowpass Filter Frequency Response (Hamming Window, N=31)');
grid on;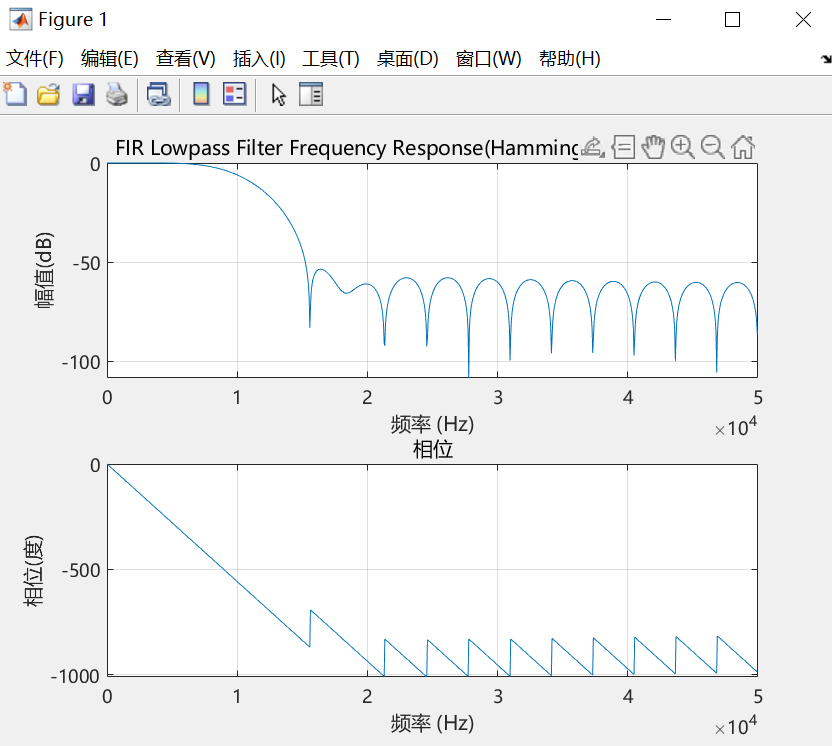

3. 量化系数 (关键！FPGA 需要整数、定点数)：

        h 是 MATLAB 算出的浮点数系数 (范围大约 -1 到 1)。

        确定系数位宽 COEFF_WIDTH (例如 16 bit)。

        确定量化格式： Q 格式 (常用 Q1.15，即 1 位符号位 + 15 位小数位)。

COEFF_WIDTH = 16;
FRAC_BITS = COEFF_WIDTH - 1; % 15 for Q1.15
h_quant = round(h * (2^FRAC_BITS)); % 放大 2^15 倍后四舍五入取整
% 饱和处理 (防止溢出)
max_val = 2^(COEFF_WIDTH-1) - 1; % 32767 for 16-bit
min_val = -2^(COEFF_WIDTH-1);     % -32768 for 16-bit
h_quant(h_quant > max_val) = max_val;
h_quant(h_quant < min_val) = min_val;

4. 生成 .coe 文件 (供 Vivado ROM IP 使用)：

% 打开文件用于写入
fid = fopen('fir_coefficients.coe', 'w');
% 写入.coe文件头 (指定Radix和系数值)
fprintf(fid, 'memory_initialization_radix = 10;\n'); % 或 2, 16
fprintf(fid, 'memory_initialization_vector = \n');
% 写入系数 (十进制整数形式，最后一个系数后面不加逗号)
for i = 1:length(h_quant)if i < length(h_quant)fprintf(fid, '%d,\n', h_quant(i));elsefprintf(fid, '%d;\n', h_quant(i)); % 最后一个系数以分号结尾end
end
fclose(fid);
disp('COE file "fir_coefficients.coe" generated.');

三、vivado 工程

整体框图如下:

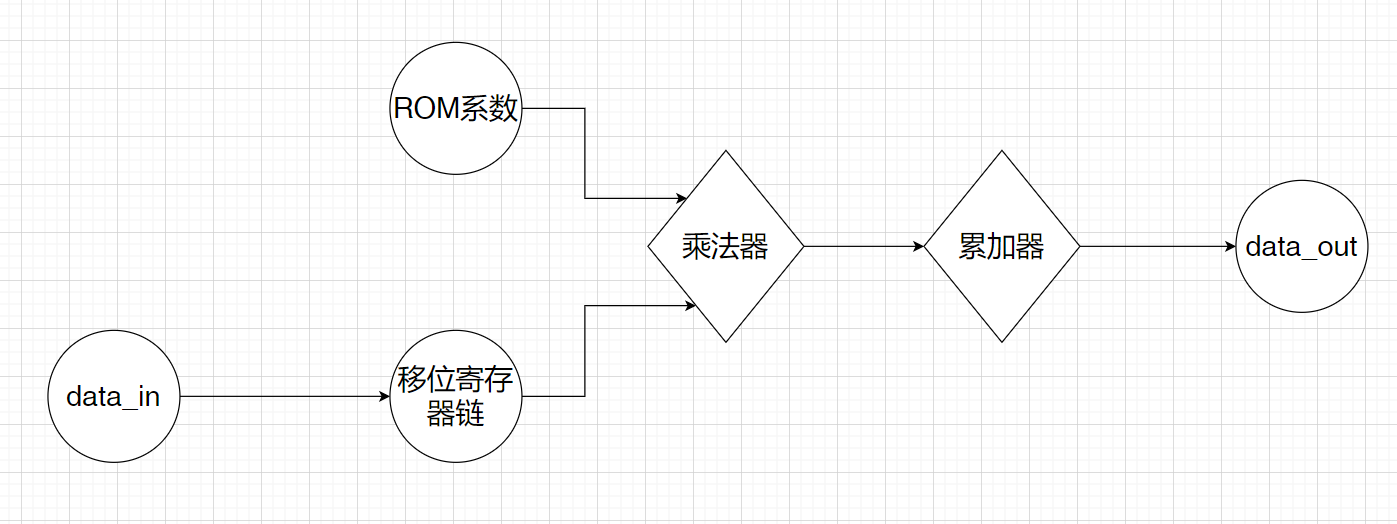
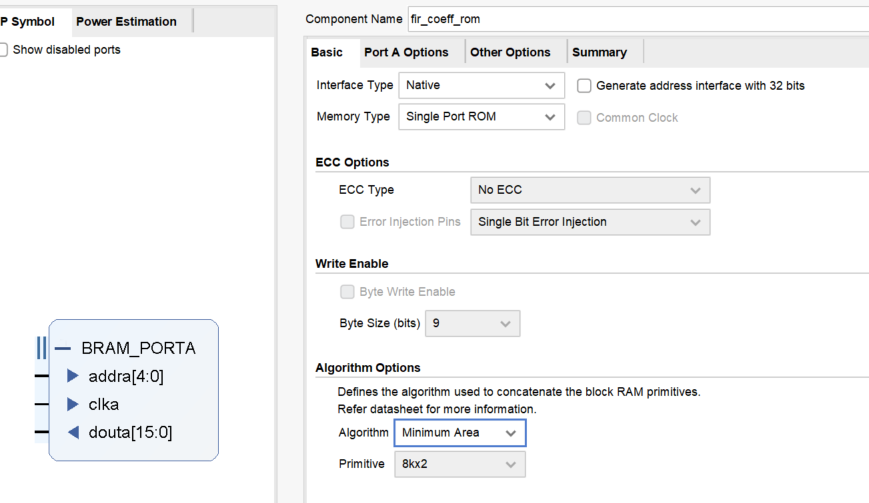
1. 创建用于存储系数的ROM (Block Memory Generator IP)

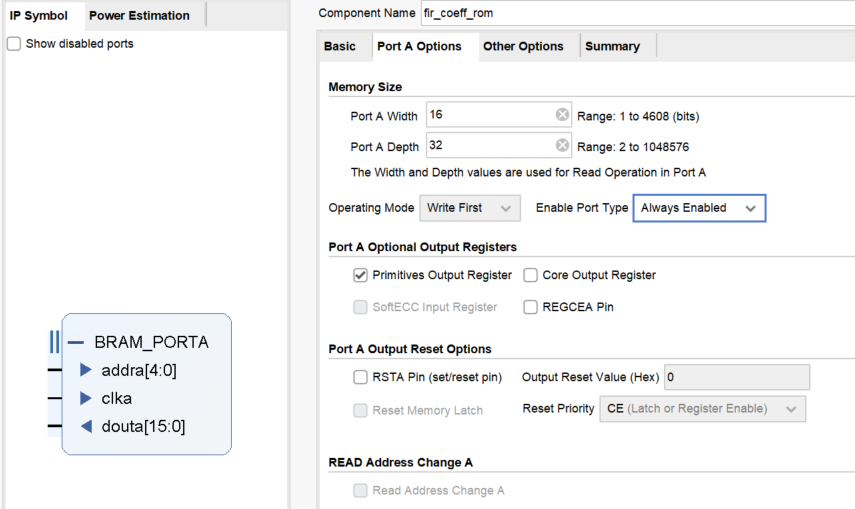
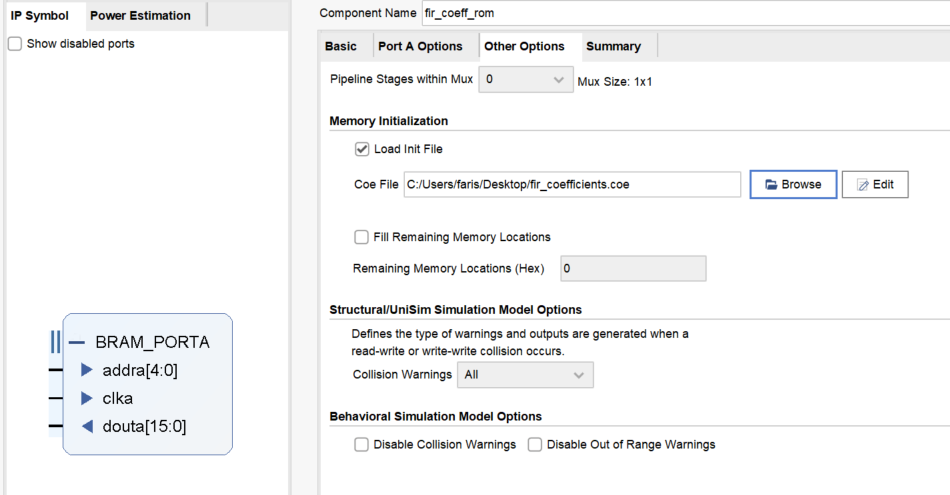
2. 实现串行FIR滤波器结构

核心思想为：

  1. 使用单个乘法器依次计算每个抽头的乘积

  2. 通过状态机精确控制计算流程

  3. 移位寄存器存储历史样本

  4. ROM存储滤波器系数

完整工作流程为：

  1. 复位阶段：所有寄存器清零，状态机归零

  2. 新样本到达：进入状态0

    • 移位寄存器更新

    • 累加器和地址初始化

  3. 乘累加阶段：状态1到TAPS-1

    • 依次计算每个抽头的乘积

    • 累加前一个抽头的计算结果

  4. 输出阶段：状态TAPS

    • 输出累加结果

    • 返回状态0等待新样本

`timescale 1ns / 1psmodule serial_fir#(parameter DATA_WIDTH = 12,parameter OUTPUT_WIDTH = 28,parameter COEFF_WIDTH = 16,parameter TAPS = 32
)(input wire clk,input wire rst,input wire signed [DATA_WIDTH - 1 : 0] data_in,output reg signed [OUTPUT_WIDTH - 1 : 0] data_out 
);
//移位寄存器链；存储当前与过去的输入样本reg signed [DATA_WIDTH-1:0] shift_reg [0:TAPS-1];//前面是每个元素的位宽，后面是一个数组及索引范围integer i;//FIR系数接收wire signed[COEFF_WIDTH-1:0] coeff_out;reg [$clog2(TAPS)-1:0] addr ;fir_coeff_rom your_instance_name (.clka(clk),    // input wire clka.addra(addr),  // input wire [4 : 0] addra.douta(coeff_out)  // output wire [15 : 0] douta
);//乘法器(为了高时钟F加流水线级)，累加器,状态寄存器reg signed[OUTPUT_WIDTH-1:0] accumulator;reg signed[$clog2(TAPS):0] state;reg signed[OUTPUT_WIDTH-1:0]product_reg;reg signed[OUTPUT_WIDTH-1:0]mult_result;always@(posedge clk or posedge rst)if(rst)beginfor(i=0; i<TAPS; i=i+1) shift_reg[i] <= 0;addr <= 0;accumulator <= 0;state <= 0;product_reg <= 0;data_out <=0;end else begincase(state)0: beginfor(i=TAPS-1; i>0; i=i-1)beginshift_reg[i] <= shift_reg[i-1];endshift_reg[0] <= data_in;state <= 1;enddefault beginif(state <= TAPS) beginmult_result <= shift_reg[addr] * coeff_out;product_reg <= mult_result;accumulator <= accumulator + product_reg;addr <= addr + 1;state <= state + 1;end else begindata_out <= accumulator;state <= 0;endendendcaseendendmodule

四、使用乘法器IP核进行硬件加速

        虽然Verilog的 * 操作符在小位宽时综合工具可能能推断出乘法器，但对于16位或更大位宽，使用Xilinx专用的DSP Slice IP核 (Multiplier) 通常性能更好、资源利用更优、时序更容易满足。

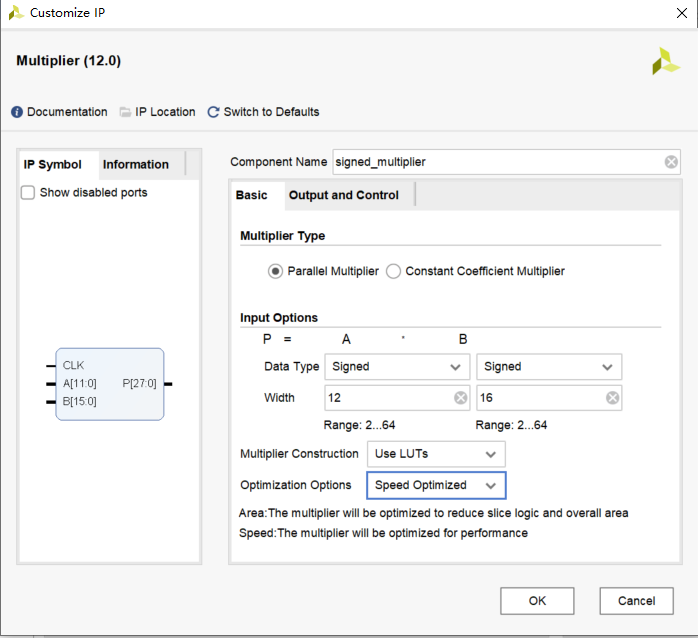
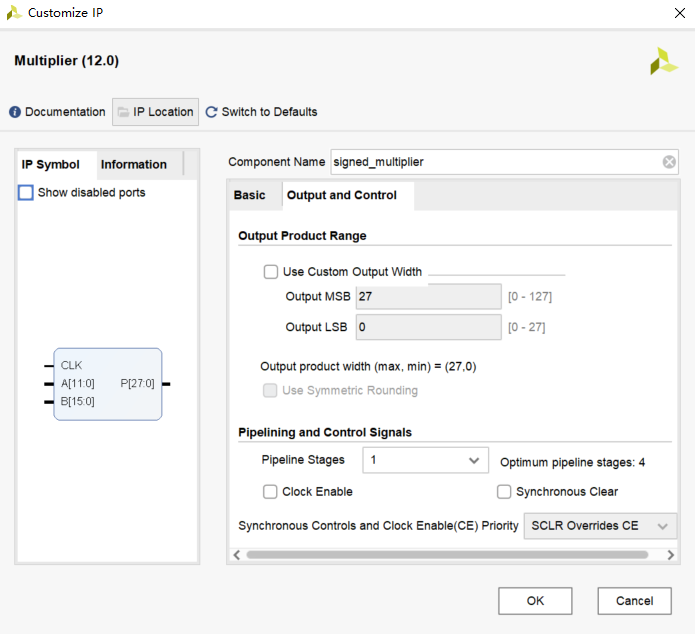
修改 serial_fir.v 代码：

        1. 找到原来的乘法操作 shift_reg[addr] * coeff_out;

        2. 同时将原来的代码进行时序状态机优化，

        2. 替换为乘法器IP核实例化：

`timescale 1ns / 1psmodule serial_fir#(parameter DATA_WIDTH = 12,parameter OUTPUT_WIDTH = 28,parameter COEFF_WIDTH = 16,parameter TAPS = 32
)(input wire clk,input wire rst,input wire signed [DATA_WIDTH - 1 : 0] data_in,output reg signed [OUTPUT_WIDTH - 1 : 0] data_out 
);// 移位寄存器链reg signed [DATA_WIDTH-1:0] shift_reg [0:TAPS-1];integer i;// FIR系数接收wire signed [COEFF_WIDTH-1:0] coeff_out;reg [$clog2(TAPS)-1:0] addr;// 状态寄存器 - 需要覆盖0到TAPS+1状态reg [$clog2(TAPS+2):0] state; // 修正位宽// 乘法器、累加器相关reg signed [OUTPUT_WIDTH-1:0] accumulator;reg signed [OUTPUT_WIDTH-1:0] product_reg;wire signed [OUTPUT_WIDTH-1:0] mult_result; // 改为wire类型// 系数ROMfir_coeff_rom coeff_rom_inst (.clka(clk),.addra(addr),.douta(coeff_out));// 乘法器IP核实例化signed_multiplier mult_inst (.CLK(clk),.A(shift_reg[addr]),.B(coeff_out),.P(mult_result));// 状态定义localparam S_LOAD  = 0;   // 加载新样本localparam S_MULT  = 1;   // 启动乘法localparam S_ACC   = 2;   // 累加结果localparam S_OUTPUT = 3;  // 输出结果always @(posedge clk or posedge rst) beginif (rst) begin// 复位所有寄存器for (i = 0; i < TAPS; i = i + 1) shift_reg[i] <= 0;addr <= 0;accumulator <= 0;state <= S_LOAD;product_reg <= 0;data_out <= 0;end else begincase (state)S_LOAD: begin// 移位寄存器更新for (i = TAPS-1; i > 0; i = i - 1) beginshift_reg[i] <= shift_reg[i-1];endshift_reg[0] <= data_in;// 初始化累加器和地址accumulator <= 0;addr <= 0;// 进入乘法状态state <= S_MULT;endS_MULT: begin// 启动乘法（结果将在下一周期出现在mult_result）// 不需要直接赋值，乘法器IP会自动计算// 存储上一个乘法结果（如果有）// 对于第一个抽头，product_reg为0// 进入累加状态state <= S_ACC;endS_ACC: begin// 累加前一个乘法结果accumulator <= accumulator + product_reg;// 存储当前乘法结果（用于下一个抽头的累加）product_reg <= mult_result;// 更新地址addr <= addr + 1;// 判断是否完成所有抽头if (addr < TAPS - 1) beginstate <= S_MULT; // 继续下一个抽头end else beginstate <= S_OUTPUT; // 所有抽头处理完成endendS_OUTPUT: begin// 累加最后一个抽头的结果accumulator <= accumulator + product_reg;// 输出最终结果data_out <= accumulator;// 返回加载状态state <= S_LOAD;endendcaseendend
endmodule

五、编写仿真文件查看波形

`timescale 1ns/1psmodule serial_fir_tb();localparam DATA_WIDTH = 12;
localparam OUTPUT_WIDTH = 28;
localparam COEFF_WIDTH = 16;
localparam TAPS = 32;
localparam CLK_PERIOD = 10;reg clk;
reg rst;
reg signed [DATA_WIDTH - 1 : 0] data_in;
wire signed [OUTPUT_WIDTH - 1 : 0] data_out ;parameter FS_REAL = 100000;
parameter REAL_PERIOD = 1.0e9/FS_REAL;
integer t;
real time_val;
parameter freq1 = 5000;
parameter freq2 = 30000;
parameter pi = 3.1415926;
parameter amplitude = (1 << (DATA_WIDTH-1))-1;//时钟生成
always #(CLK_PERIOD/2) clk = ~clk;//实例化模块
serial_fir#(.DATA_WIDTH(DATA_WIDTH),.OUTPUT_WIDTH(OUTPUT_WIDTH),.COEFF_WIDTH(COEFF_WIDTH),.TAPS(TAPS)
) uut(.clk(clk),.rst(rst),.data_in(data_in),.data_out(data_out) 
);//初始化
initial beginclk = 0;rst = 1;data_in = 0;#(CLK_PERIOD*2) rst = 0;//测试1：单位冲击响应（验证滤波系数）
data_in = (1 << (DATA_WIDTH-2));
#(CLK_PERIOD);
data_in = 0;
#(CLK_PERIOD*(TAPS*10));//测试2：混合频率信号（验证滤波效果）
//localparam FS_REAL = 100000.0;
//localparam REAL_PERIOD = 1.0e9 / FS_REAL;
//integer t;
//real time_val;
//real freq1 = 5000;
//real freq2 = 30000;
//real pi = 3.1415926;
//real amplitude = (1 << (DATA_WIDTH-1))-1;for(t=0; t<500; t=t+1) begintime_val = t*(REAL_PERIOD/1.0e9);//第t个样本对应的实际时间sdata_in = $rtoi(amplitude * (0.6 * $sin(2 * pi * freq1 * time_val) + 0.4 * $sin(2 * pi * freq2 * time_val)));$display("t = %d, time_val = %f, data_in = %d， data_out = %d", t, time_val, data_in, data_out);#(REAL_PERIOD);
end//结束仿真
#(CLK_PERIOD*100);
$finish;end//波形记录
initial begin$dumpfile("waveform.vcd");$dumpvars(0,uut);
endendmodule

仿真结果如下图所示：

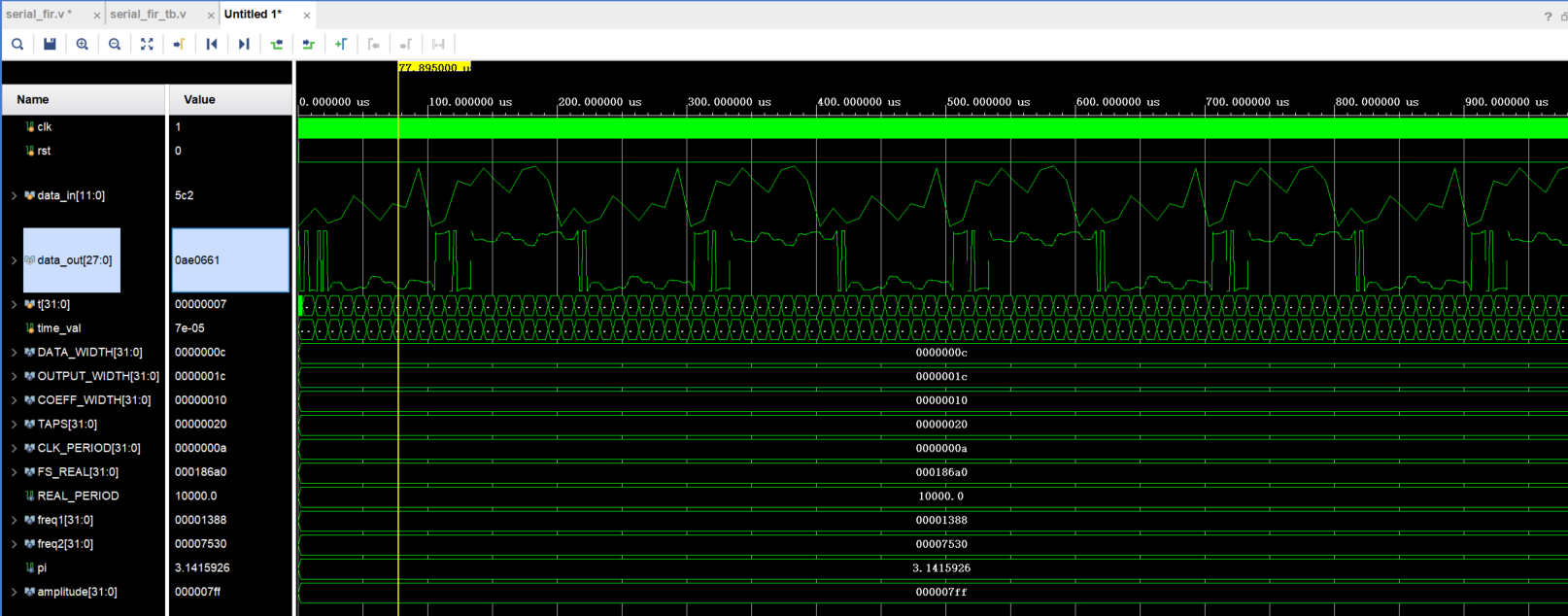
六、MATLAB进行FFT分析

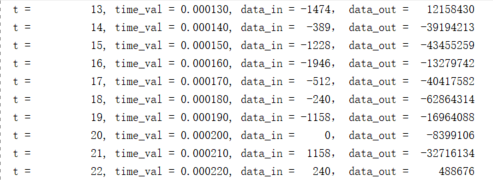
将生成的dumpfile文件复制到txt文档然后导入MATLAB进行FFT分析（一部分如下）

MATLAB代码如下：

% FIR滤波器频谱分析完整代码
% 功能：读取数据文件，计算并绘制data_in和data_out的频谱，验证滤波效果% --------------------------
% 1. 读取数据文件
% --------------------------
% 确保数据文件与当前MATLAB脚本在同一目录，或使用绝对路径
data_filename = 'fir_data_clean.txt';  % 数据文件名
data = load(data_filename);            % 读取空格分隔的纯数值文件% 提取各列数据
t = data(:, 1);           % 时间索引
data_in = data(:, 2);     % 输入信号
data_out = data(:, 3);    % 输出信号% 验证数据读取结果
fprintf('成功读取数据，共 %d 个样本\n', length(t));
fprintf('时间范围: t = %d 至 %d\n', t(1), t(end));% --------------------------
% 2. 配置信号参数
% --------------------------
FS = 100000;              % 采样率 (Hz)，与仿真中的FS_REAL一致
N = length(data_in);      % 数据点数
Nyquist = FS / 2;         % 奈奎斯特频率 (Hz)% --------------------------
% 3. 计算FFT并处理频谱
% --------------------------
% 对输入信号计算FFT
dc_in = mean(data_in);                   % 计算直流分量
fft_in = fft(data_in - dc_in);           % 去除直流分量后计算FFT
fft_mag_in = abs(fft_in) / N * 2;        % 幅度归一化（双边谱转单边谱）
fft_mag_in(1) = fft_mag_in(1) / 2;       % 修正直流分量幅度% 对输出信号计算FFT
dc_out = mean(data_out);
fft_out = fft(data_out - dc_out);
fft_mag_out = abs(fft_out) / N * 2;
fft_mag_out(1) = fft_mag_out(1) / 2;% 生成频率轴（单位：Hz）
freq = (0:N-1) * FS / N;% --------------------------
% 4. 绘制时域波形
% --------------------------
figure('Name', '时域波形', 'Position', [100, 100, 1000, 600]);
subplot(2, 1, 1);
plot(t, data_in, 'b-', 'LineWidth', 1);
xlabel('时间索引 t');
ylabel('幅度');
title('输入信号 data_in 时域波形');
grid on;subplot(2, 1, 2);
plot(t, data_out, 'r-', 'LineWidth', 1);
xlabel('时间索引 t');
ylabel('幅度');
title('输出信号 data_out 时域波形');
grid on;
sgtitle('时域波形对比');% --------------------------
% 5. 绘制频谱图（0至奈奎斯特频率）
% --------------------------
figure('Name', '频谱对比', 'Position', [200, 200, 1000, 600]);% 输入信号频谱
subplot(2, 1, 1);
plot(freq(1:N/2), fft_mag_in(1:N/2), 'b-', 'LineWidth', 1.2);
xlabel('频率 (Hz)');
ylabel('幅度');
title('data_in 频谱（5kHz + 30kHz 混合信号）');
grid on;
xlim([0, Nyquist]);  % 显示0至50kHz
hold on;
% 标记关键频率
plot([5000, 5000], ylim, 'r--', 'LineWidth', 1);    % 5kHz（目标保留频率）
plot([30000, 30000], ylim, 'g--', 'LineWidth', 1);  % 30kHz（目标衰减频率）
legend('信号幅度', '5kHz（通带）', '30kHz（阻带）', 'Location', 'best');% 输出信号频谱
subplot(2, 1, 2);
plot(freq(1:N/2), fft_mag_out(1:N/2), 'r-', 'LineWidth', 1.2);
xlabel('频率 (Hz)');
ylabel('幅度');
title('data_out 频谱（滤波后）');
grid on;
xlim([0, Nyquist]);
hold on;
plot([5000, 5000], ylim, 'r--', 'LineWidth', 1);
plot([30000, 30000], ylim, 'g--', 'LineWidth', 1);
legend('信号幅度', '5kHz（通带）', '30kHz（阻带）', 'Location', 'best');sgtitle('输入输出信号频谱对比');% --------------------------
% 6. 定量分析关键频率成分
% --------------------------
% 查找5kHz附近的频率索引
[idx_5k, ~] = min(abs(freq - 5000));
mag_in_5k = fft_mag_in(idx_5k);    % 输入信号5kHz幅度
mag_out_5k = fft_mag_out(idx_5k);  % 输出信号5kHz幅度% 查找30kHz附近的频率索引
[idx_30k, ~] = min(abs(freq - 30000));
mag_in_30k = fft_mag_in(idx_30k);  % 输入信号30kHz幅度
mag_out_30k = fft_mag_out(idx_30k);% 输出信号30kHz幅度% 计算衰减比和增益
attenuation_ratio = mag_in_30k / mag_out_30k;  % 30kHz衰减倍数（越大越好）
gain_5k = mag_out_5k / mag_in_5k;              % 5kHz增益（应接近1）% 打印分析结果
fprintf('\n===== 频谱定量分析结果 =====\n');
fprintf('5kHz信号幅度: 输入=%.2f, 输出=%.2f\n', mag_in_5k, mag_out_5k);
fprintf('30kHz信号幅度: 输入=%.2f, 输出=%.2f\n', mag_in_30k, mag_out_30k);
fprintf('30kHz衰减比: %.2f 倍（理想低通滤波器应远大于1）\n', attenuation_ratio);
fprintf('5kHz增益: %.2f（理想应接近1）\n', gain_5k);% 判断滤波效果
if attenuation_ratio > 5 && gain_5k > 0.5fprintf('\n结论: 滤波效果符合预期，30kHz高频被有效衰减，5kHz低频保留良好。\n');
elsefprintf('\n结论: 滤波效果不理想，需检查FIR滤波器系数或内部逻辑。\n');
end

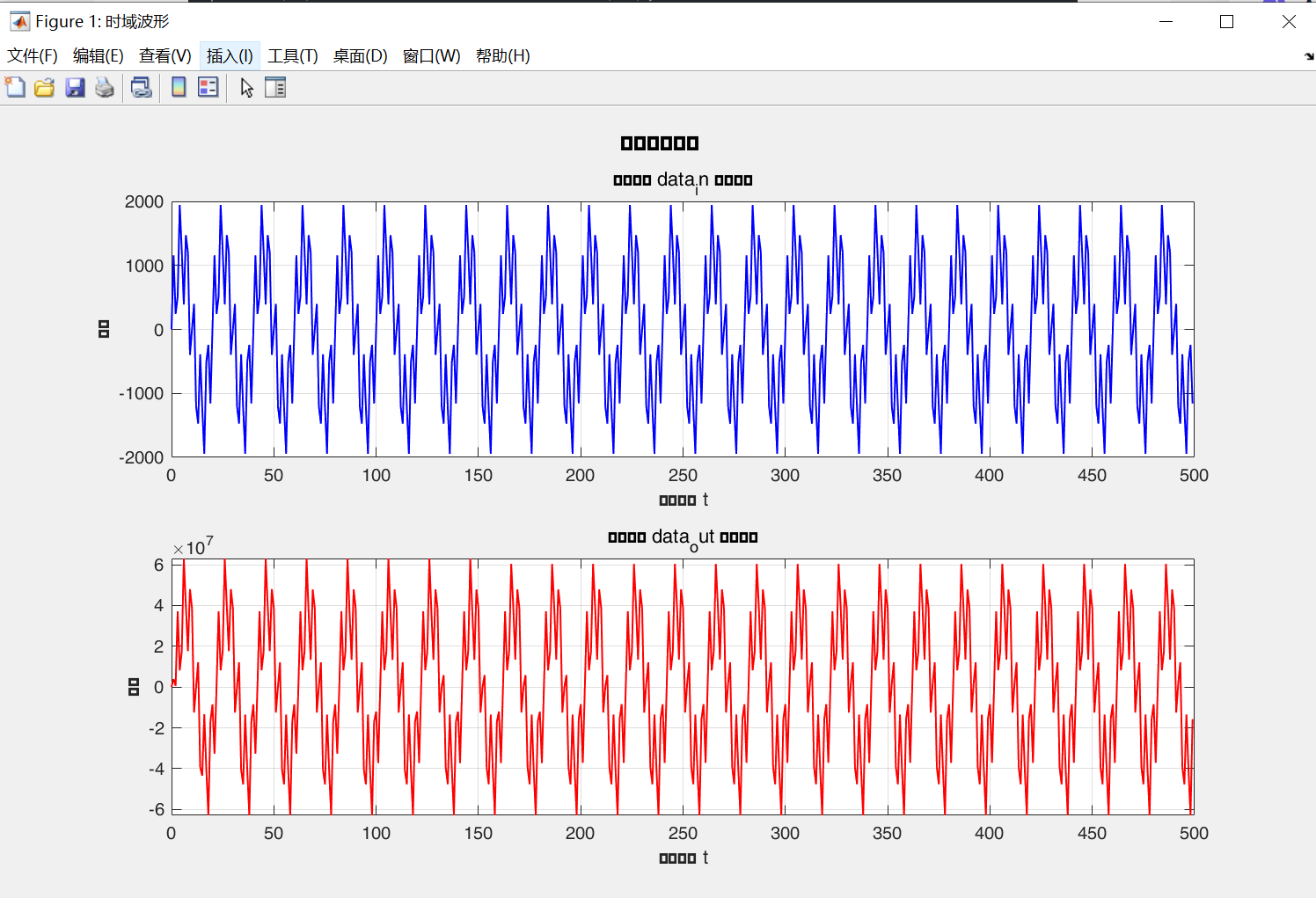
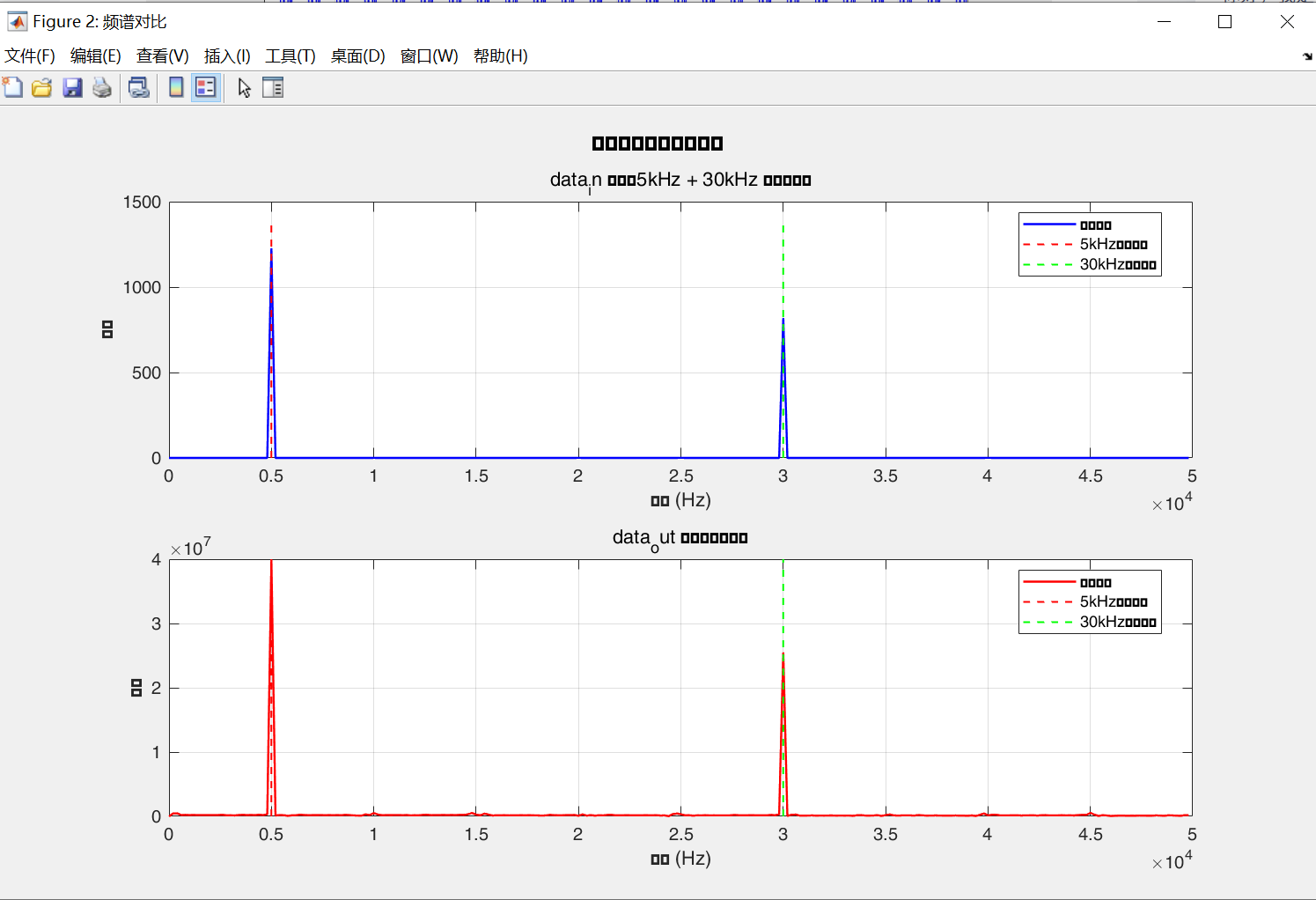
从结果来看，滤波效果符合预期，原因如下：

1. 频谱分析

  • 输入频谱：data_in 在 5kHz 和 30kHz 处均有明显峰值，符合 “5kHz + 30kHz 混合信号” 的设计预期。
  • 输出频谱：data_out 仅保留了 5kHz 处的峰值，30kHz 处的峰值几乎完全被衰减，说明 FIR 滤波器成功实现了 “保留 5kHz 低频、衰减 30kHz 高频” 的低通滤波功能。

2. 结论

当前频谱结果表明，FIR 滤波器的滤波效果符合设计目标，30kHz 高频被有效抑制，5kHz 低频被完整保留。

后续改进方向：可向并行设计靠拢

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
如若转载，请注明出处：http://www.pswp.cn/web/93074.shtml
繁体地址，请注明出处：http://hk.pswp.cn/web/93074.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

JPrint免费的Web静默打印控件：PDF打印中文乱码异常解决方案

JPrint免费的Web静默打印控件：PDF打印中文乱码异常解决方案

文章目录JPrint是什么&#xff1f;中文乱码&#xff08;Using fallback font xxx for xxxx&#xff09;1.字体嵌入2.客户机字体安装开源地址相关目录导航使用文档端口号修改代理使用场景打印服务切换中文乱码解决方案 JPrint是什么&#xff1f; JPrint是一个免费开源的可视化静…
阅读更多...
MFT 在零售行业的实践案例与场景：加速文件集成与业务协作的高效方案

MFT 在零售行业的实践案例与场景：加速文件集成与业务协作的高效方案

零售行业竞争激烈、数字化转型迭代迅速&#xff0c;业务对数据与档案的传输、处理和整合要求极高。无论是新品上市市场数据&#xff0c;还是供应链物流单据&#xff0c;集成方式不论是通过API或是档案传输, 对于传输的稳定性,安全性与性能, 都会直接影响决策效率与顾客体验。MF…
阅读更多...
OSG+Qt —— 笔记1 - Qt窗口加载模型（附源码）

OSG+Qt —— 笔记1 - Qt窗口加载模型（附源码）

🔔 OSG/OsgEarth 相关技术、疑难杂症文章合集（掌握后可自封大侠 ⓿_⓿）（记得收藏，持续更新中…） OSG+Qt所用版本皆为： Vs2017+Qt5.12.4+Osg3.6.5+OsgQt(master) 效果 代码（需将cow.osg、reflect.rgb拷贝至工程目录下） OsgForQt.ui main.cpp
阅读更多...
开源安全云盘存储：Hoodik 实现端到端数据加密，Docker快速搭建

开源安全云盘存储：Hoodik 实现端到端数据加密，Docker快速搭建

以下是对 Hoodik 的简单介绍&#xff1a; Hoodik 是一个使用 Rust 和 Vue 开发的轻量级自托管安全云存储解决方案采用了非对称RSA密钥对和AES混合加密策略&#xff0c;从文件存储加密到数据链路加密&#xff0c;全程保证数据安全支持Docker一键私有部署&#xff0c;数据和服务…
阅读更多...
[C++] Git 使用教程（从入门到常用操作）

[C++] Git 使用教程（从入门到常用操作）

1. Git 简介 Git 是一款分布式版本控制系统&#xff0c;用来跟踪文件变化、协作开发、管理项目版本。 它是开源的&#xff0c;由 Linus Torvalds 在 2005 年开发&#xff0c;广泛用于开源与企业项目中。 2. 安装 Git Windows 前往 Git 官网 下载并安装。 安装时建议勾选 Git…
阅读更多...
实盘回测一体的期货策略开发：tqsdk获取历史数据并回测，附python代码

实盘回测一体的期货策略开发：tqsdk获取历史数据并回测，附python代码

原创内容第969篇&#xff0c;专注AGI&#xff0c;AI量化投资、个人成长与财富自由。 星球好多同学希望说说实盘&#xff0c;我们就从实盘开始吧。 我们选择tqsdk给大家讲解&#xff0c;tqsdk支持免费注册&#xff0c;使用模拟账户&#xff0c;历史和实时数据&#xff0c;方便…
阅读更多...
大模型推理框架vLLM 中的Prompt缓存实现原理

大模型推理框架vLLM 中的Prompt缓存实现原理

背景&#xff1a;为什么需要Prompt缓存模块&#xff1f;在大模型问答多轮对话应用场景中&#xff0c;不同请求的 Prompt 往往有相同的前缀&#xff0c;比如&#xff1a;第一次问答&#xff1a;你是一名专业的电子产品客服&#xff0c;负责回答客户关于手机产品的咨询。请根据以…
阅读更多...
Python之Django使用技巧（附视频教程）

Python之Django使用技巧（附视频教程）

概述 Django 是一个高级的 Python Web 框架&#xff0c;遵循 “batteries-included”&#xff08;内置电池&#xff09;理念&#xff0c;提供了构建 Web 应用所需的大部分组件&#xff0c;让开发者可以专注于业务逻辑而不是底层细节。视频教程&#xff1a;https://pan.quark.cn…
阅读更多...
sqli-labs通关笔记-第44关 POST字符型堆叠注入(单引号闭合 手工注入+脚本注入3种方法)

sqli-labs通关笔记-第44关 POST字符型堆叠注入(单引号闭合 手工注入+脚本注入3种方法)

目录 一、堆叠注入 二、源码分析 1、代码审计 2、SQL注入安全性分析 三、堆叠手注法 1、进入靶场 2、正确用户名密码登录 3、堆叠注入 4、查看数据库 四、联合手注法 1、获取列数 2、确认回显位 3、获取数据库名 4、获取表名 5、获取列名 6、获取字段 7、总结…
阅读更多...
从深度伪造到深度信任：AI安全的三场攻防战

从深度伪造到深度信任：AI安全的三场攻防战

前言当大模型开始“睁眼”看世界&#xff0c;伪造者也开始“闭眼”造世界。2025 WAIC释放出的信号很明确&#xff1a;没有AI安全底座&#xff0c;就没有产业智能化的高楼。WAIC 把“安全”摆在与“创新”同等重要的位置&#xff0c;形成了“1 份共识框架&#xff0b;2 份重磅报…
阅读更多...
【C++】哈希的应用：位图和布隆过滤器

【C++】哈希的应用：位图和布隆过滤器

目录 一、位图 1.1 位图的概念 1.2 位图的实现 1.3 位图的应用 二、布隆过滤器 2.1 布隆过滤器的提出 2.2 布隆过滤器的概念 2.3 布隆过滤器的插入和查找 2.4 布隆过滤器的删除 2.5 布隆过滤器的优点 2.6 布隆过滤器的缺点 一、位图 1.1 位图的概念 1. 面试题 给4…
阅读更多...
C语言：指针（4）

C语言：指针（4）

1. 回调函数回调函数就是指通过函数指针调用的函数。如果将函数指针作为参数传递给另一个函数&#xff0c;另一个函数根据指针来调这个函数&#xff0c;那么被调用的函数就是回调函数。回调函数不是由这个函数的实现方直接调用&#xff0c;而是在特定的条件下由另一方调用的。例…
阅读更多...
vue--video使用动态src时，视频不更新

vue--video使用动态src时，视频不更新

问题描述 在 Vue项目中&#xff0c;尝试动态更新 标签的 元素 src 属性来切换视频时&#xff0c;遇到了一个问题&#xff1a;即使 src 已更改&#xff0c;浏览器仍不显示视频。 <template><video width"100%" height"100%" controlspause"…
阅读更多...
计算机视觉--opencv(代码详细教程）（一）

计算机视觉--opencv(代码详细教程）（一）

在计算机视觉的广袤领域中&#xff0c;OpenCV 是一座极为关键的里程碑。无论是在前沿的学术研究&#xff0c;还是在蓬勃发展的工业界&#xff0c;OpenCV 凭借其强大的功能与高效的性能&#xff0c;为开发者提供了丰富的图像处理和计算机视觉算法&#xff0c;助力无数项目落地。…
阅读更多...
物联网通讯协议-MQTT、Modbus、OPC

物联网通讯协议-MQTT、Modbus、OPC

引言在物联网迅速发展的今天&#xff0c;设备间的通信协议扮演着至关重要的角色。它们是不同设备、系统之间实现数据交换的桥梁。本文将详细介绍三种在物联网领域广泛应用的通讯协议——MQTT、Modbus和OPC&#xff0c;包括它们的基础概念、特点及在C#中的实现方法。一、MQTT协议…
阅读更多...
牛客周赛R104 小红的矩阵不动点

牛客周赛R104 小红的矩阵不动点

D-小红的矩阵不动点_牛客周赛 Round 104 赛时这道题卡了一段时间&#xff0c;赛时代码如下&#xff1a; #include<bits/stdc.h> using namespace std; int ans,h; int a[505][505]; signed main(){ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);int n,m;cin>…
阅读更多...
Rust面试题及详细答案120道（19-26）-- 所有权与借用

Rust面试题及详细答案120道（19-26）-- 所有权与借用

《前后端面试题》专栏集合了前后端各个知识模块的面试题&#xff0c;包括html&#xff0c;javascript&#xff0c;css&#xff0c;vue&#xff0c;react&#xff0c;java&#xff0c;Openlayers&#xff0c;leaflet&#xff0c;cesium&#xff0c;mapboxGL&#xff0c;threejs&…
阅读更多...
Jenkins + SonarQube 从原理到实战三：SonarQube 打通 Windows AD（LDAP）认证与踩坑记录

Jenkins + SonarQube 从原理到实战三：SonarQube 打通 Windows AD（LDAP）认证与踩坑记录

前言 在前两篇文章中&#xff0c;已经介绍了 SonarQube 的部署 以及 通过 sonar-cxx 插件实现 C/C 代码扫描。 本篇将重点讲 如何让 SonarQube 对接 Windows AD&#xff08;LDAP&#xff09;&#xff0c;实现域账号登录和基于 AD 组的权限管理。 一、背景与需求分析 需求分析…
阅读更多...
[AI React Web] 包与依赖管理 | `axios`库 | `framer-motion`库

[AI React Web] 包与依赖管理 | `axios`库 | `framer-motion`库

第七章&#xff1a;包与依赖管理 在我们使用open-lovable的旅程中&#xff0c;已经探索了它如何管理对话状态&#xff08;第一章&#xff1a;对话状态管理&#xff09;、将创意转化为可运行代码&#xff08;第二章&#xff1a;AI代码生成管道&#xff09;、如何在安全的虚拟环…
阅读更多...
PanSou 一款开源网盘搜索项目，集成前后端，一键部署，开箱即用

PanSou 一款开源网盘搜索项目，集成前后端，一键部署，开箱即用

PanSou 网盘搜索API PanSou是一个高性能的网盘资源搜索API服务&#xff0c;支持TG搜索和自定义插件搜索。系统设计以性能和可扩展性为核心&#xff0c;支持并发搜索、结果智能排序和网盘类型分类。 项目地址&#xff1a;https://github.com/fish2018/pansou 特性&#xff08…
阅读更多...
最新文章

Copyright @ 2022~2023