主成分分析（PCA）和数据降维是机器学习和统计学中处理高维数据的核心工具。下面用清晰的结构解释其概念、原理和应用：

---

一、数据降维（Dimensionality Reduction）

1. 是什么？

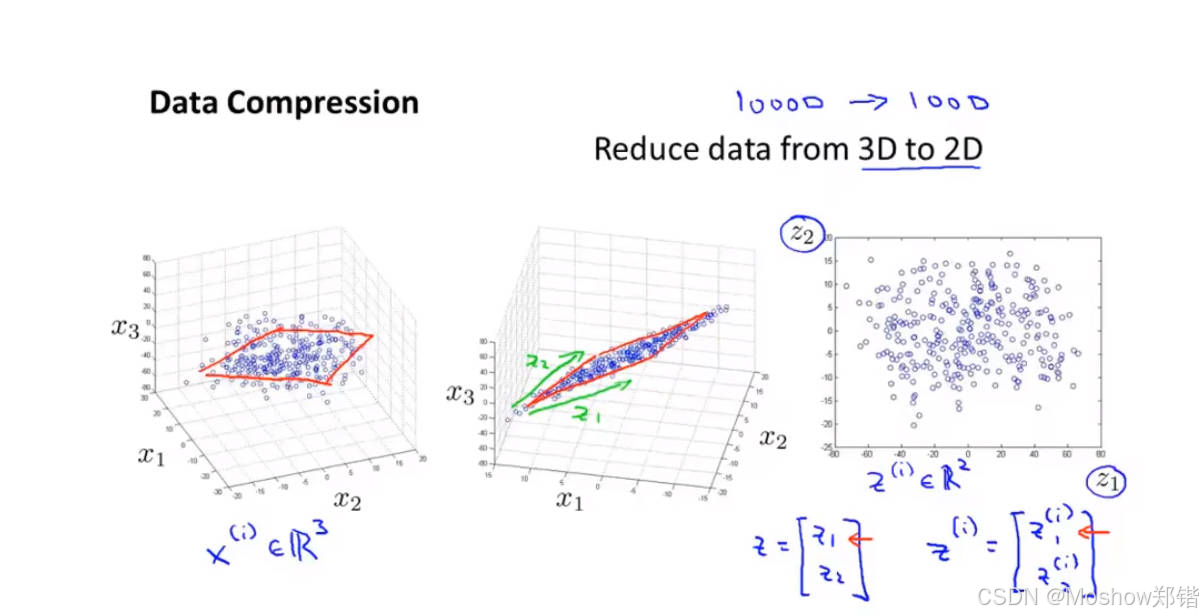
• 目标：将高维数据（特征多）转换为低维表示（特征少），同时保留关键信息。

• 为什么需要？

  • 维度灾难（Curse of Dimensionality）：特征过多导致计算效率低、模型过拟合、噪声放大。

  • 可视化需求：人类只能理解 ≤3 维空间，降维后可直观展示数据。

  • 去除冗余：许多特征可能高度相关（如“身高(cm)”和“身高(inch)”）。

2. 两类常用方法

类型	代表方法	核心思想
特征选择	过滤法、嵌入法	直接筛选原始特征（保留部分列）
特征提取	PCA、t-SNE	创建新特征组合（生成新特征列）

---

二、主成分分析（PCA）

1. 是什么？

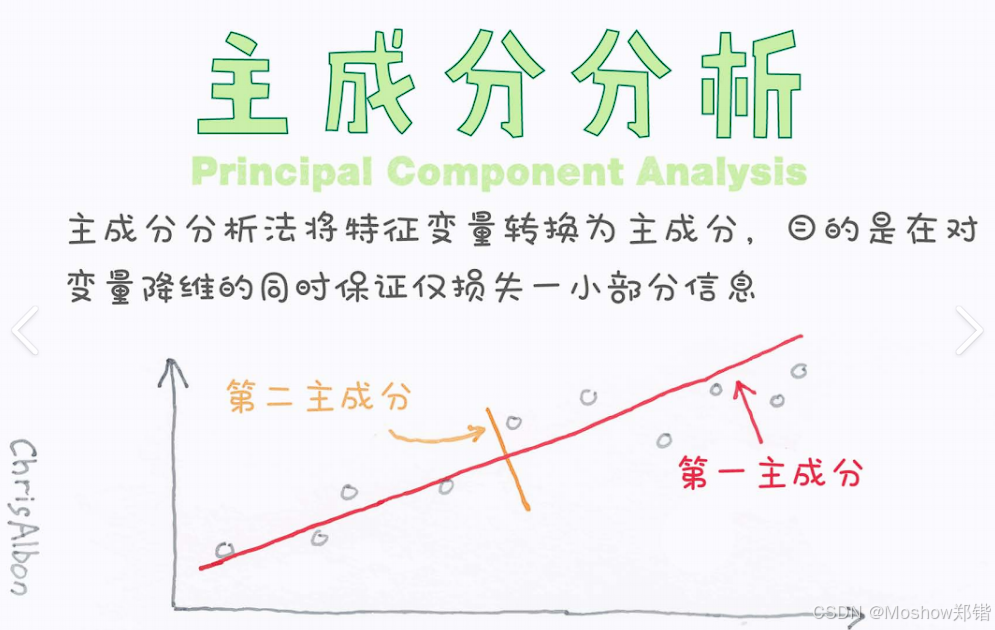
• 本质：一种线性特征提取方法，通过正交变换将原始特征重组为互不相关的“主成分”。

• 目标：找到数据方差最大的方向（即信息最集中的方向），作为新坐标轴。

2. 核心思想

• 最大化方差：新坐标轴（主成分）的方向是数据投影后方差最大的方向。

• 正交性：每个主成分与前一主成分正交（无相关性）。

• 重要性排序：第一主成分（PC1）保留最多信息，后续依次递减。

3. 数学原理（关键步骤）

1. 中心化数据：将每个特征减去其均值（使数据均值为0）。

2. 计算协方差矩阵：反映特征间的线性相关性。

3. 特征值分解：

   • 协方差矩阵的特征向量 → 主成分方向

   • 特征值 → 主成分的方差大小（特征值越大，保留信息越多）

4. 选择主成分：

   • 按特征值从大到小排序，选择前 kk 个主成分（k<k< 原始维度）。

5. 投影数据：将原始数据投影到选定的 kk 个主成分上，得到降维后的数据。

4. 可视化理解

• 原始数据：分布在倾斜的椭圆中（特征相关）。

• PC1：沿椭圆长轴方向（方差最大）。

• PC2：沿短轴方向（与PC1正交，方差次大）。
  → 若只保留PC1，数据从2维降至1维，但保留了主要结构。

https://miro.medium.com/v2/resize:fit:1400/1*Upj7eTtSLsK0yFjDwYfGJA.gif

---

三、PCA的实际应用

1. 典型场景

• 图像处理：将像素压缩（如人脸识别中的特征提取）。

• 基因数据分析：处理数万个基因表达维度。

• 金融风控：降低股票收益率相关性维度。

• 数据预处理：为SVM、回归等模型减少噪声和过拟合。

2. 输出结果解读

• 主成分（PC）：新特征，是原始特征的线性组合（如 PC1=0.7×身高+0.3×体重PC1=0.7×身高+0.3×体重）。

• 解释方差比：每个主成分保留原始信息的百分比（累计达80%~95%即足够）。

---

四、PCA的优缺点

优点	缺点
减少过拟合，提升模型泛化能力	仅捕获线性关系（非线性需用核PCA）
去除特征间的相关性	降维后特征失去物理意义（难解释）
计算高效（基于线性代数）	对异常值敏感（需提前标准化数据）
无需标签（无监督方法）	方差小但重要的特征可能被丢弃

---

五、关键注意事项

1. 标准化先行：若特征量纲不同（如身高 vs 收入），必须先标准化（均值为0，标准差为1），否则高方差特征会主导结果。

2. 选择 kk 的方法：

   • 肘部法则：绘制累计解释方差比曲线，选择拐点。

   • 保留阈值：通常保留累计方差 ≥85% 的主成分。

3. PCA ≠ 特征选择：
   PCA生成的是新特征（原始特征的线性组合），而非筛选原始特征。

---

六、代码示例（Python）

from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler# 1. 标准化数据
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)# 2. 执行PCA（保留95%方差）
pca = PCA(n_components=0.95) 
X_pca = pca.fit_transform(X_scaled)# 输出结果
print("保留主成分数量:", pca.n_components_)
print("各主成分解释方差比:", pca.explained_variance_ratio_)

七、题目解析

主成分分析（PCA）的主要用途在于（）

A数据清洗

B数据降维

C数据预测

D数据分类

正确答案：B

解析：

A. 数据清洗：错误。虽然主成分分析可以帮助识别异常值或噪声，但它不是专门用于数据清洗的工具。数据清洗通常涉及处理缺失值、纠正错误等操作。C. 数据预测：错误。主成分分析本身不直接进行数据预测。它是一种探索性数据分析方法，主要目的是减少数据的维度，而不是预测未来的趋势或结果。D. 数据分类：错误。主成分分析也不是一种分类算法。尽管它可以作为预处理步骤在机器学习分类任务中使用，以降低特征空间的维度，但它的主要目的并不是进行分类。综上所述，主成分分析的主要用途是数据降维，因此正确答案是B。

---

总结

• 数据降维：高维数据 → 低维表示，提升效率并保留信息。

• PCA：通过线性变换找到方差最大的正交方向（主成分），按重要性保留前 kk 个。

• 核心价值：用少量不相关的新特征替代大量原始特征，解决维度灾难问题。