昨天,我初步掌握了 0/1 背包问题的理论基础和标准解法。今天,我将这种思想应用到了更广泛的场景中。今天的几道题,乍一看和背包没什么关系,但通过巧妙的数学转化,它们的核心都变成了 0/1 背包问题。
这让我深刻体会到,学习算法不仅仅是学习模板,更重要的是学习一种建模能力——将一个看似全新的问题,转化为我们熟悉的模型来求解。为了加深理解,我对每个适用的问题都同时实现了二维和一维的解法,以观察它们之间的联系和区别。
一、实战演练:识别伪装的背包问题
1. LeetCode 1049. 最后一块石头的重量 II
题目描述: 有一堆石头,用整数数组 stones 表示。其中 stones[i] 是第 i 块石头的重量。每一回合,从中选出任意两块石头,然后将它们一起粉碎…最后,最多只会剩下一块石头。返回此石头最小的可能重量。
-
学习感悟: 这个问题等价于将所有石头分成两堆
A和B,并让它们的重量差|sum(A) - sum(B)|最小。为了实现这一点,我们需要让其中一堆的重量sum(A)尽可能地接近总重量的一半。这完美地转化为了一个 0/1 背包问题:- 背包容量:
target = total_sum // 2 - 物品:
stones数组中的每一个stone - 物品重量/价值:
stone的重量 - 目标: 在容量为
target的背包里,能装下的最大重量是多少?
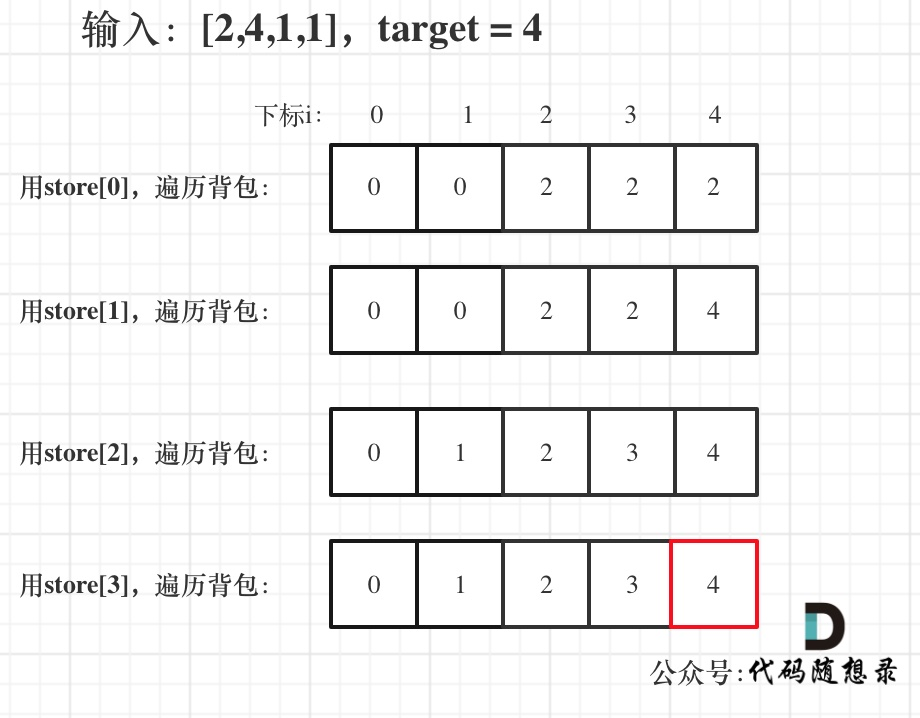
- 背包容量:
-
资源包:
* 题目/文章: https://programmercarl.com/1049.%E6%9C%80%E5%90%8E%E4%B8%80%E5%9D%97%E7%9F%B3%E5%A4%B4%E7%9A%84%E9%87%8D%E9%87%8FII.html
* 视频讲解: https://www.bilibili.com/video/BV14M411C7oV
我的实现 1:二维 DP
class Solution:def lastStoneWeightII(self, stones: List[int]) -> int:total_sum = sum(stones)target = total_sum // 2n = len(stones)# dp[i][j]: 从0..i-1号石头中任选,放入容量j的背包,能达到的最大重量dp = [[0] * (target + 1) for _ in range(n + 1)]for i in range(1, n + 1):stone_weight = stones[i - 1]for j in range(target + 1):if j < stone_weight:dp[i][j] = dp[i - 1][j] # 装不下,不装else:# 装或者不装dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - stone_weight] + stone_weight)sum_A = dp[n][target]sum_B = total_sum - sum_Areturn sum_B - sum_A
我的实现 2:一维 DP (空间优化)
class Solution:def lastStoneWeightII(self, stones: List[int]) -> int:total_sum = sum(stones)target = total_sum // 2# dp[j]:容量为j的背包,能装下的最大重量dp = [0] * (target + 1)for stone_weight in stones:# 倒序遍历,保证每个石头只用一次for j in range(target, stone_weight - 1, -1):dp[j] = max(dp[j], stone_weight + dp[j - stone_weight])sum_A = dp[target]sum_B = total_sum - sum_Areturn sum_B - sum_A
2. LeetCode 494. 目标和
题目描述: 给你一个整数数组 nums 和一个整数 target 。向数组中的每个整数前添加 '+' 或 '-'。返回可以通过上述方法构造的、运算结果等于 target 的不同表达式的数目。
- 学习感悟: 这道题是计数型 DP,但同样可以转化为背包问题。假设加
+的子集和为P,加-的子集和为N。我们有P - N = target和P + N = total_sum。两式相加得2P = target + total_sum,即P = (target + total_sum) / 2。- 背包模型: 问题变成了:从
nums中挑选出一些数,使其和恰好为new_target = (target + total_sum) / 2,共有多少种挑法? - DP 定义:
dp[j]表示和为j的组合有多少种。
- 背包模型: 问题变成了:从
- 资源包:
- 题目/文章: https://programmercarl.com/0494.%E7%9B%AE%E6%A0%87%E5%92%8C.html
- 视频讲解: https://www.bilibili.com/video/BV1o8411j73x
我的实现 1:二维 DP
class Solution:def findTargetSumWays(self, nums: List[int], target: int) -> int:total_sum = sum(nums)if abs(target) > total_sum or (total_sum + target) % 2 != 0:return 0new_target = (total_sum + target) // 2n = len(nums)# dp[i][j]: 从0..i-1号数中任选,和为j的组合数dp = [[0] * (new_target + 1) for _ in range(n + 1)]dp[0][0] = 1 # 用0个数凑成和为0,有一种方法(什么都不选)for i in range(1, n + 1):num = nums[i - 1]for j in range(new_target + 1):if j < num:dp[i][j] = dp[i - 1][j] # 不选numelse:# 组合数 = (不选num的方法数) + (选num的方法数)dp[i][j] = dp[i - 1][j] + dp[i - 1][j - num]return dp[n][new_target]
我的实现 2:一维 DP (空间优化)
class Solution:def findTargetSumWays(self, nums: List[int], target: int) -> int:total_sum = sum(nums)if abs(target) > total_sum or (total_sum + target) % 2 != 0:return 0new_target = (total_sum + target) // 2# dp[j]:和为 j 的组合有多少种dp = [0] * (new_target + 1)dp[0] = 1for num in nums:# 倒序遍历,保证每个数只用一次for j in range(new_target, num - 1, -1):dp[j] += dp[j - num]return dp[new_target]
3. LeetCode 474. 一和零
题目描述: 给你一个二进制字符串数组 strs 和两个整数 m 和 n 。请你找出 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。
-
学习感悟: 这道题是二维费用的 0/1 背包,是背包问题的一个重要变种。
- 背包容量: 是一个二维的
(m, n),分别代表0和1的容量。 - 物品:
strs数组中的每个字符串。 - 物品重量: 每个字符串的重量也是二维的
(count_zeros, count_ones)。 - 物品价值: 每个字符串价值都是
1。
- 背包容量: 是一个二维的
-
DP 定义:
dp[i][j]表示用i个0和j个1能构成的最大子集长度。 -
状态转移:
dp[i][j] = max(dp[i][j], 1 + dp[i - count_zeros][j - count_ones])。 -
遍历顺序: 因为是 0/1 背包,两个表示容量的循环
i和j都必须倒序遍历。 -
资源包:
- 题目/文章: https://programmercarl.com/0474.%E4%B8%80%E5%92%8C%E9%9B%B6.html
- 视频讲解: https://www.bilibili.com/video/BV1rW4y1x7ZQ
我的实现:二维费用背包
class Solution:def findMaxForm(self, strs: List[str], m: int, n: int) -> int:# dp[i][j]:用 i 个 0 和 j 个 1 能构成的最大子集长度dp = [[0] * (n + 1) for _ in range(m + 1)]for s in strs: # 遍历物品count_zeros = s.count('0')count_ones = s.count('1')# 倒序遍历背包的两个维度容量for i in range(m, count_zeros - 1, -1):for j in range(n, count_ones - 1, -1):dp[i][j] = max(dp[i][j], 1 + dp[i - count_zeros][j - count_ones])return dp[m][n]
总结
今天我更深刻地理解了 0/1 背包问题的泛用性。它不仅仅是一个求最大价值的模型,通过改变 dp 数组的定义(求最大重量、求组合数、求可行性)和状态转移的方式,它可以解决各种各样的问题。识别问题背后的背包模型,并正确地进行转化,是解决这类 DP 问题的关键所在。从一维费用到二维费用,背包问题的世界真是广阔。




)
)

安全管理(3)-行级访问控制)
的核心区别,以及 Wi-Fi 技术未来的发展方向)

进阶)》)
)


)
:AI界“冰火两重天“,GPT-5陷入热议,DeepSeek R2模型训练受阻?)



