前言
物理信息神经网络(Physics-Informed Neural Networks, PINNs)是一种结合深度学习与物理定律的神经网络方法,旨在解决涉及偏微分方程(PDEs)的问题。以下是对该问题的详细解答:
-
物理信息神经网络的定义与核心思想
物理信息神经网络(PINNs)是一种将物理定律嵌入到神经网络中的方法,通过将物理方程、边界条件和初始条件作为约束条件,指导神经网络的训练过程。这种方法能够利用已知的物理定律来增强模型的泛化能力,尤其在数据稀缺或数据质量较低的情况下具有显著优势。 -
PINNs的核心机制
• 物理约束的嵌入:PINNs通过将物理方程(如偏微分方程)和边界条件嵌入到神经网络的损失函数中,使模型在训练过程中自动满足物理约束。例如,损失函数通常包括物理残差项和边界条件的残差项。
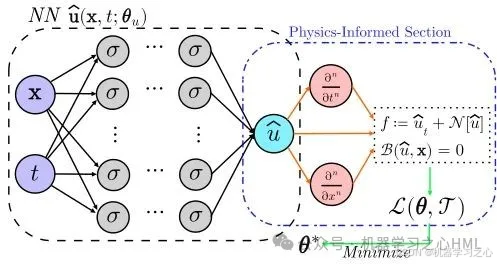
• 数据驱动与物理驱动的结合:PINNs可以同时利用数据和物理知识进行建模,即使在数据量较少的情况下也能获得较好的预测结果。
• 灵活性与可扩展性:PINNs可以处理非线性问题、参数化问题以及多尺度问题,并且能够处理复杂的物理系统,如流体力学、材料科学、地球物理学等。 -
PINNs的应用领域
PINNs在多个领域中得到了广泛应用,包括但不限于:
• 流体力学与流体动力学:用于模拟流体流动、湍流、波传播等。
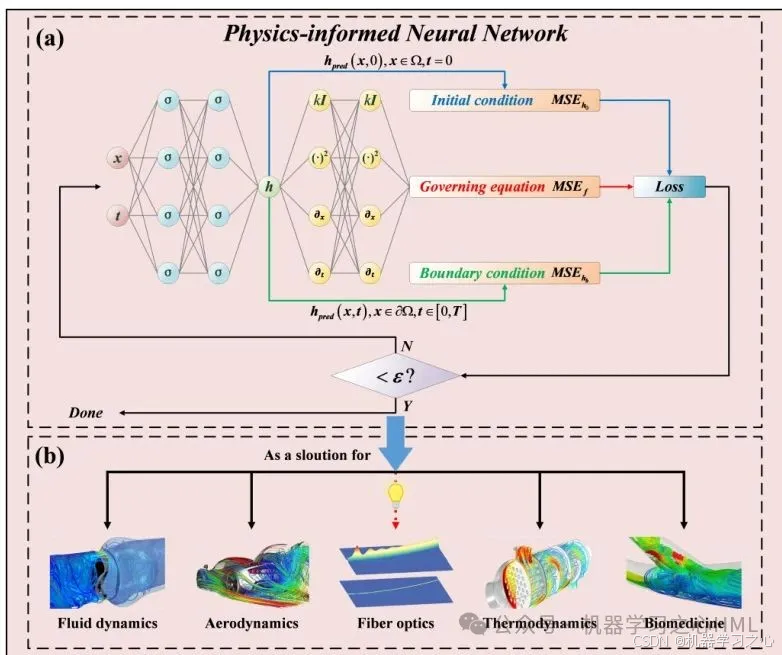
材料科学与工程:用于模拟材料行为、微结构力学、异质材料等。
• 生物医学与医学成像:用于图像重建、医学成像、生物信号处理等。
• 能源与环境科学:用于模拟能源系统、气候建模、环境动力学等。
4. PINNs的优势与挑战
• 优势:
• 数据效率高:在数据稀缺的情况下,PINNs能够通过物理约束提高模型的泛化能力。
• 可解释性强:物理约束的引入增强了模型的可解释性,有助于理解物理系统的复杂行为。
• 计算效率高:相比传统数值方法(如有限元法),PINNs在某些情况下具有更高的计算效率。
• 挑战:
• 优化难度:PINNs的训练过程可能较为复杂,需要仔细调整超参数(如损失函数权重、学习率等)。
• 物理方程的表示:如何将复杂的物理方程和边界条件准确地嵌入到神经网络中仍是一个挑战。
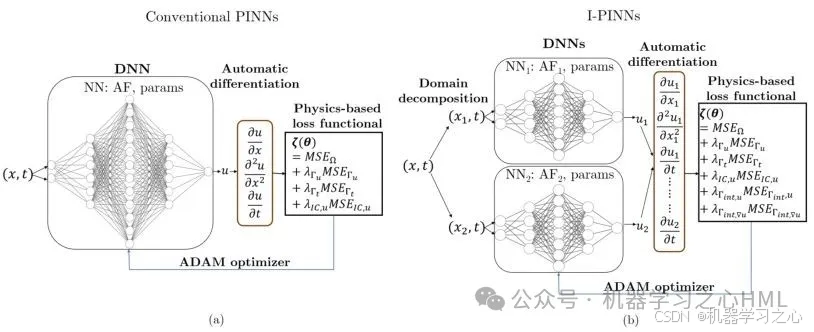
5. PINNs的未来发展方向
• 自适应物理信息神经网络(SAPINNs) :通过引入自适应权重和动态调整物理约束,进一步提高模型的灵活性和适应性。
• 多尺度与多物理场耦合:发展能够处理多尺度、多物理场耦合问题的PINNs模型。
• 与量子计算结合:探索PINNs与量子计算的结合,以解决更复杂的物理问题。
结论
物理信息神经网络(PINNs)是一种将深度学习与物理定律相结合的创新方法,能够有效解决涉及偏微分方程的复杂问题。通过将物理约束嵌入到神经网络中,PINNs在数据稀缺、数据质量低或物理系统复杂的情况下具有显著优势。尽管在优化和物理方程表示方面仍存在挑战,但PINNs在多个领域中展现出广阔的应用前景。
代码功能
MATLAB 代码实现了一个物理信息神经网络(Physics-Informed Neural Network, PINN),用于结合数据驱动与物理规律进行回归预测。以下是详细分析:
一、代码功能概述
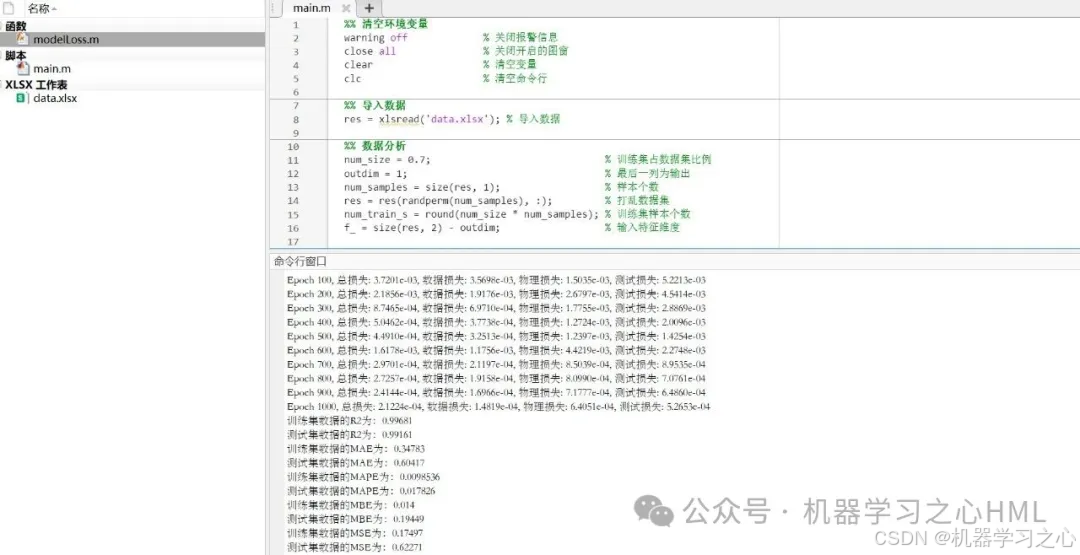
- main.m
• 功能:主程序,完成数据导入、预处理、网络构建、训练、测试与可视化。
• 步骤:
• 导入数据并划分训练集和测试集;
• 数据归一化;
• 构建全连接神经网络(含3个隐藏层);
• 使用包含物理约束的损失函数进行训练;
• 评估模型性能(RMSE、R²、MAE、MAPE、MBE、MSE);
• 绘制预测结果与误差图。 - modelLoss.m
• 功能:自定义损失函数,计算数据损失与物理损失。
• 步骤:
• 计算数据拟合损失(MSE);
• 在物理点上计算物理残差(使用有限差分近似导数);
• 组合得到总损失:总损失 = 数据损失 + λ * 物理损失;
• 返回梯度用于反向传播。
二、逻辑关联
• main.m 在训练循环中调用 modelLoss 函数计算损失和梯度;
• modelLoss 利用 dlarray 和 dlgradient 实现自动微分,支持物理残差的反向传播;
• 物理点的生成和物理损失的引入是 PINN 的核心,使模型既拟合数据又遵守物理规律。
三、算法步骤
训练流程(PINN): - 数据准备与划分;
- 构建神经网络;
- 在训练数据点上计算数据损失;
- 在物理点上计算物理残差(近似微分);
- 组合损失并反向传播更新网络;
- 循环直至收敛。
四、技术路线
• 深度学习框架:使用 MATLAB 的 dlnetwork 和自动微分(DLToolbox);
• 物理建模:通过有限差分法近似微分项,引入物理残差;
• 优化算法:Adam 优化器;
• 评估指标:RMSE, R², MAE, MAPE, MBE, MSE;
• 可视化:训练过程损失曲线、预测对比图、误差分布、拟合图。

运行环境
• 软件:MATLAB R2024b或更高版本(需 Deep Learning Toolbox);
• 数据格式:Excel 文件(data.xlsx),最后一列为输出。
数据集
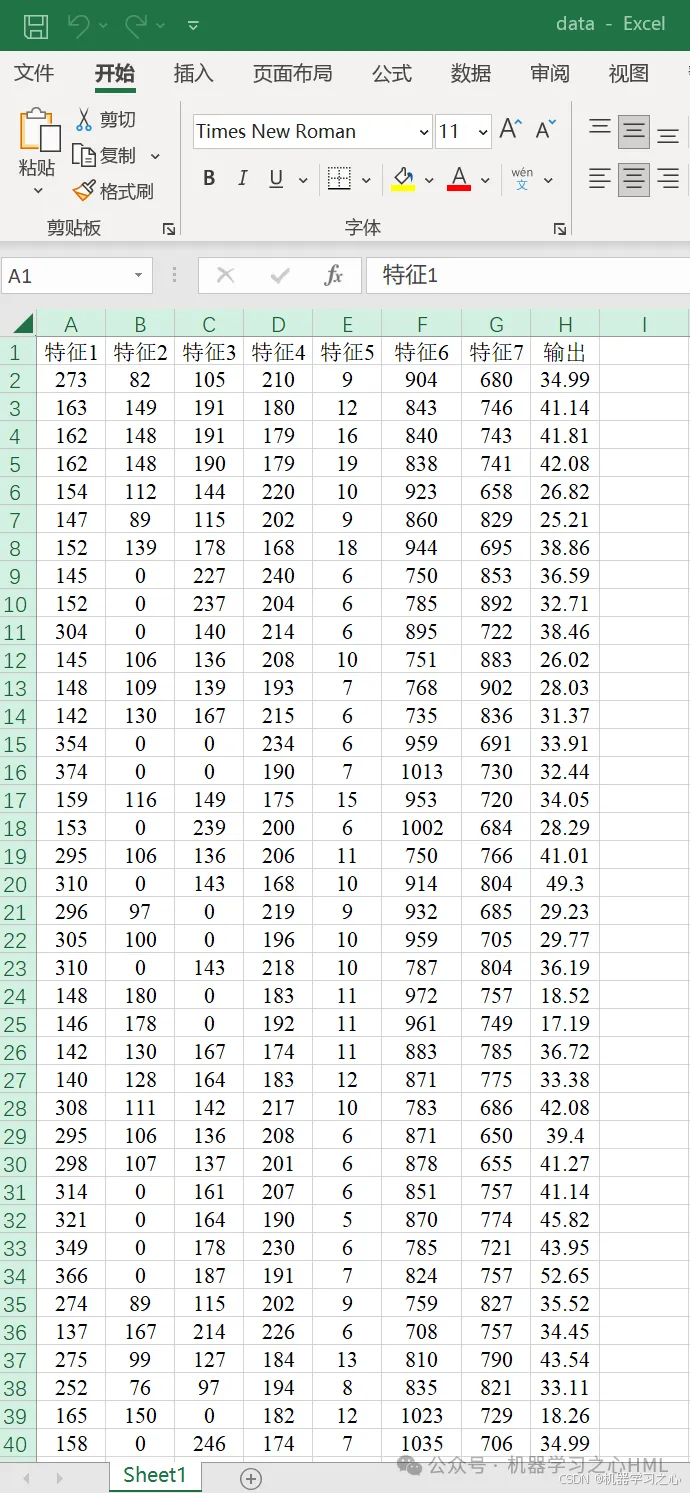
运行效果
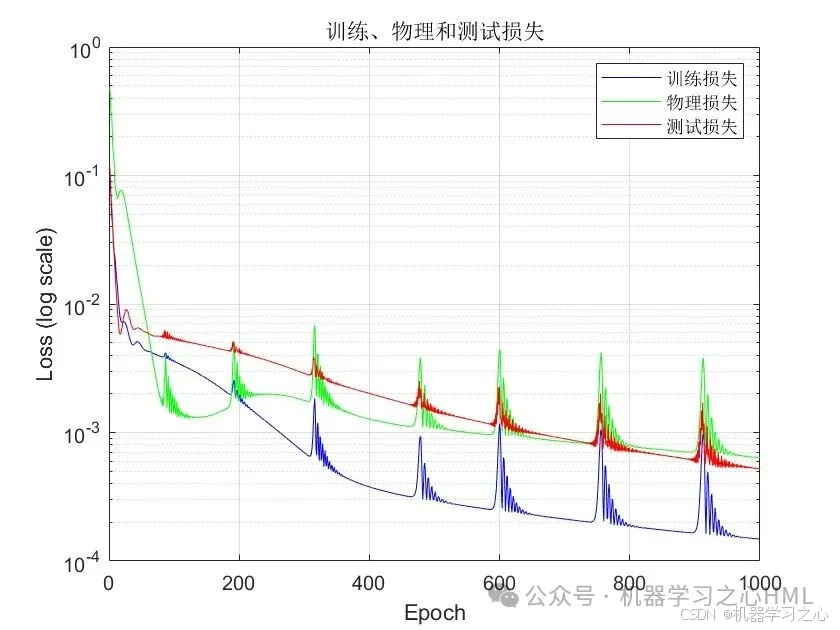
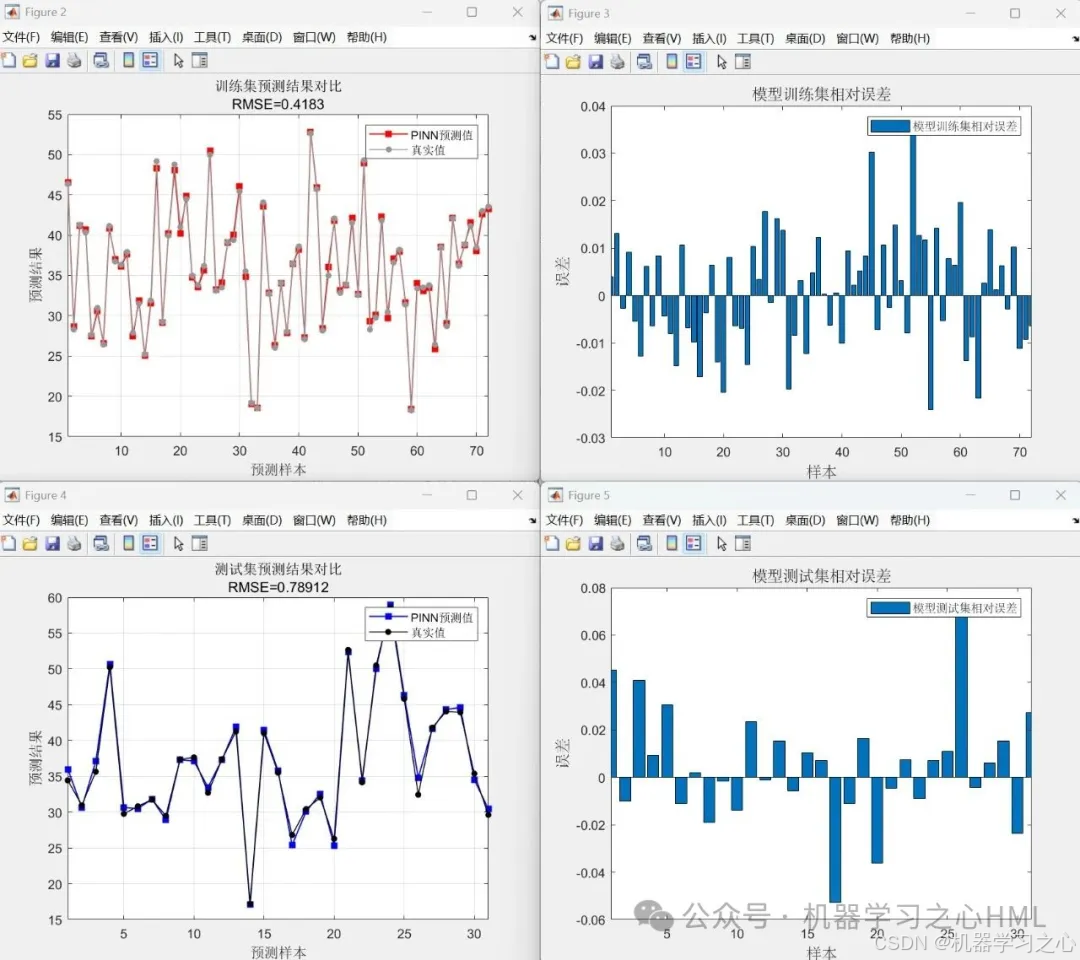
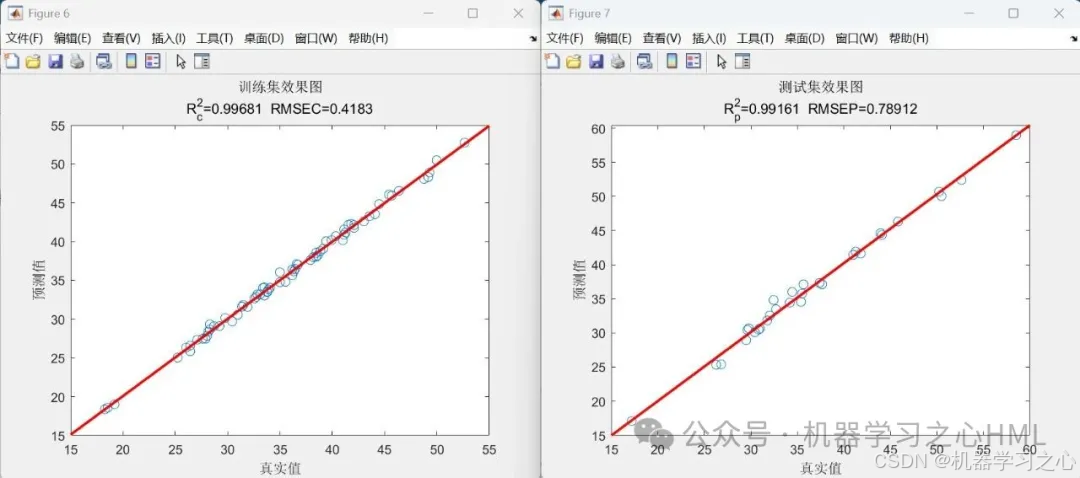
PINN 核心特征在代码中的体现
- 物理约束的引入 (modelLoss.m)
% 使用有限差分法近似计算导数
% 定义物理方程残差(以常微分方程 du/dt + u = 0 为例)
% 计算物理损失
体现了PINN的核心:不仅拟合数据,还强制网络满足物理规律(微分方程)。
-
复合损失函数 (modelLoss.m)
% 组合总损失 = 数据损失 + λ * 物理损失
PINN的标志性特征——将物理知识作为正则化项加入损失函数。 -
物理点生成 (main.m)
% 生成物理点(用于计算物理残差)
num_physics = 1000;
X_physics = rand(f_, num_physics);
PINN需要在物理域内采样点来评估物理残差,这些点不需要有标签数据。 -
物理损失权重 (main.m)
lambda_phys = 0.1; % 物理损失项的权重
通过超参数λ平衡数据拟合与物理约束的重要性。 -
训练过程中同时优化两种损失 (main.m)
% 计算包含物理约束的损失和梯度
[totalLoss, dataLoss, physLoss, gradients] = dlfeval(@modelLoss, net, P_train_dl, T_train_dl, X_physics_dl, lambda_phys);
在每次训练迭代中同时考虑数据误差和物理一致性。
PINN在本代码中的具体实现流程
- 数据准备:准备带标签的训练数据
- 物理点采样:在输入域内随机生成物理点
- 网络前向传播:同时计算数据点和物理点的输出
- 物理残差计算:使用有限差分法近似微分项
- 复合损失计算:结合数据误差和物理残差
- 反向传播:同时优化数据拟合和物理一致性
- 循环训练:不断调整网络参数以满足双重约束
核心思想
代码完整实现了PINN的核心思想:
• ✅ 引入了物理方程作为软约束
• ✅ 使用复合损失函数平衡数据拟合和物理一致性
• ✅ 在无标签的物理点上评估物理残差
• ✅ 通过超参数控制物理约束的强度
• ✅ 同时优化数据误差和物理残差
PINN与传统神经网络的根本区别——将物理先验知识 explicitly 嵌入到学习过程中,而不仅仅依赖数据驱动。
部分源码
.lineNode {font-size: 10pt; font-family: Menlo, Monaco, Consolas, "Courier New", monospace; font-style: normal; font-weight: normal; }
%% 清空环境变量
warning off % 关闭报警信息
close all % 关闭开启的图窗
clear % 清空变量
clc % 清空命令行
%% 导入数据
res = xlsread('data.xlsx'); % 导入数据
%% 数据分析
num_size = 0.7; % 训练集占数据集比例
outdim = 1; % 最后一列为输出
num_samples = size(res, 1); % 样本个数
res = res(randperm(num_samples), :); % 打乱数据集
num_train_s = round(num_size * num_samples); % 训练集样本个数
f_ = size(res, 2) - outdim; % 输入特征维度
%% 划分训练集和测试集
P_train = res(1: num_train_s, 1: f_)';
T_train = res(1: num_train_s, f_ + 1: end)';
M = size(P_train, 2);
P_test = res(num_train_s + 1: end, 1: f_)';
T_test = res(num_train_s + 1: end, f_ + 1: end)';
N = size(P_test, 2);
%% 数据归一化
[P_train, ps_input] = mapminmax(P_train, 0, 1);
P_test = mapminmax('apply', P_test, ps_input);
[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);
%% 转换为dlarray格式
P_train_dl = dlarray(P_train, 'CB'); % 特征在行,样本在列
T_train_dl = dlarray(t_train, 'CB');
P_test_dl = dlarray(P_test, 'CB');
T_test_dl = dlarray(t_test, 'CB');
%% 生成物理点(用于计算物理残差)
% 假设输入特征包含时间和空间信息,这里在[0,1]范围内随机生成物理点
num_physics = 1000; % 物理点数量
X_physics = rand(f_, num_physics); % 随机生成物理点
X_physics_dl = dlarray(X_physics, 'CB'); % 转换为dlarray
%% 创建PINN模型
layers = [featureInputLayer(f_, 'Name', 'input')fullyConnectedLayer(64, 'Name', 'fc1')





)
完全指南)



:sizeof和strlen细节强化之“做题篇”)


线程--多线程及通讯)




)