目录
- 插入排序
- 例子
- 时间复杂度
- java代码
- 希尔排序(缩小增量排序)
- 例子
- 时间复杂度
- java代码
相关文章
- 学习数据结构理论+算法时间复杂度
- 学习有序二叉树+平衡二叉树+红黑树
- 学习冒泡排序+选择排序并使用java写代码
- 学习插入排序+希尔排序并使用java写代码
- 学习堆排序+基数排序并使用java写代码
- 学习递归+归并排序+快速排序并使用java写代码
插入排序:
- 认为数组当中的第一个数值是已经排好序的数值;
- 定义一个游标,从第二个数值开始不断地向后进行遍历;
- 游标指向的数值插入到已经拍好序的数组当中。
例子:
- 定义一个游标 i ,从第一个开始遍历;
- 定义一个游标 j ,指向 i 的前一个数值;
- 对应的 j+1 指向要插入的数值;
- j 应当要比 j+1 小,如果 j > j+1 ,交换位置。
待排序组:5、7、4、1、3、0、2、6,用插入排序进行排序,步骤如下:

- j 指向5,j+1 指向7,5<7,不动;
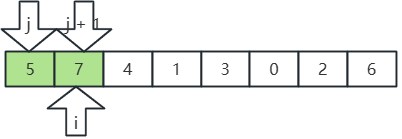
- 继续,i, j,j+1 后移,
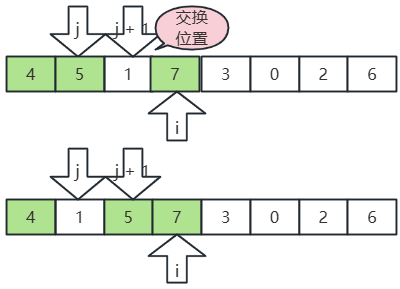
- j 指向7,j+1 指向4,7>4,交换位置;
- j 指向5,j+1 指向4,5>4,交换位置;
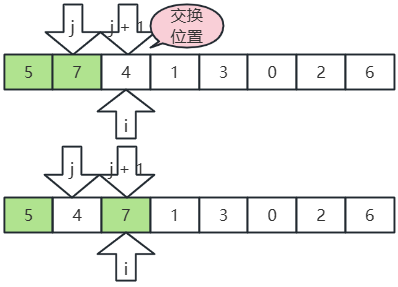
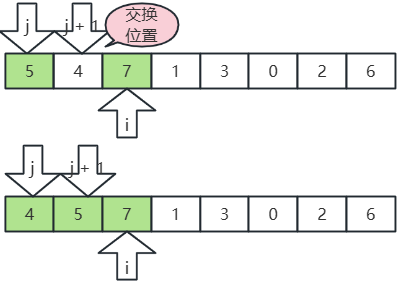
- 继续,i, j,j+1 后移,
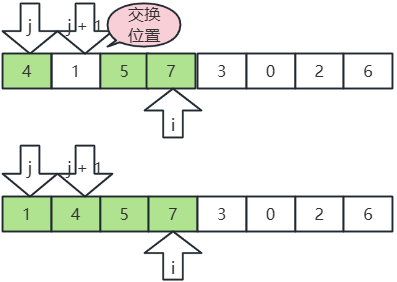
- j 指向7,j+1 指向1,7>2,交换位置;
- j 指向5,j+1 指向1,5>1,交换位置;
- j 指向4,j+1 指向1,4>1,交换位置;
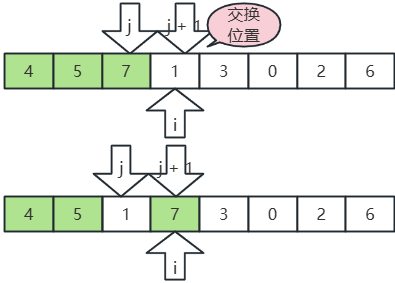
- 继续,i, j,j+1 后移,
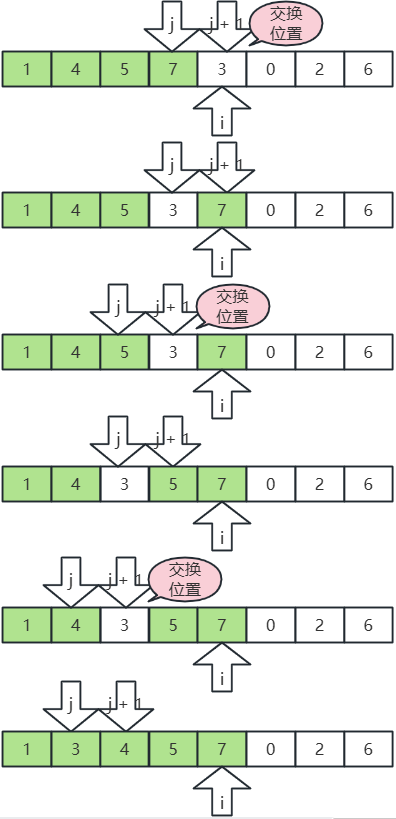
- j 指向7,j+1 指向3,7>3,交换位置;
- j 指向5,j+1 指向3,5>3,交换位置;
- j 指向4,j+1 指向3,4>3,交换位置;
- j 指向1,j+1 指向3,1<3,不动;
- ……
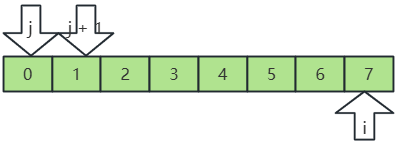
- 这样一直交换插入,直到插入排序完成。
时间复杂度:
| 数据(默认从第二个数据开始) | 移动次数(理想情况没有中断) |
|---|---|
| 下标是1的数据 | 1 |
| 下标是2的数据 | 2 |
| 下标是3的数据 | 3 |
| 下表是4的数据 | 4 |
| …… | …… |
| 下标的x-1的数据 | x-1 |
等差数列求和公式:y=(1+x−1)(x−1)2y=\frac{(1+x-1)(x-1)}{2}y=2(1+x−1)(x−1)
得到时间复杂度是:O(n2)O(n^2)O(n2)
缺点: 越小的数值在后面移动的次数越多
java代码:
package com.xxx;import java.util.Arrays;//插入排序
public class InsertSort {public static void main(String[] args) {int[] arr = {5,7,4,1,3,0,2,6};sort(arr);System.out.println(Arrays.toString(arr));}public static void sort(int[] arr) {for(int i=1;i<arr.length;i++) {//i指向的数据插入到前边已经拍好的数组当中for(int j=i-1;j>=0;j--) {//j 和 j+1 指向的数据进行比较,交换if(arr[j]>arr[j+1]) {int temp = arr[j];arr[j] = arr[j+1];arr[j+1] = temp;}else {break;}}}}
}
插入:
定义游标j指向i的前一个数据,j和j+1指向的数据进行交换,若j+1的值小,则j和j+1指向的值进行交换,j–;继续比较,知道j+1的值大,或着j=0停止。
希尔排序(缩小增量排序):
- 将数组按照数组长度的一半为间隔(步长)进行分组(奇偶无所谓,第一组为3个,剩下的均是两两一组),组内进行插入排序
- 将数组按照数组长度的一半的一半为间隔进行分组,组内进行插入排序,多个分组来回交替插入排序;
- 将数组按照数组长度的一半的一半的一半为间隔进行分组,组内进行插入排序;
- ……
- 直到步长为1,整个数组作为一组,进行插入配许,结束。
例子:
待排序组:5、7、4、1、3、0、2、6,用希尔排序进行排序,步骤如下:
- 先分组:8个数值,8/2=4,每隔四个为一组;
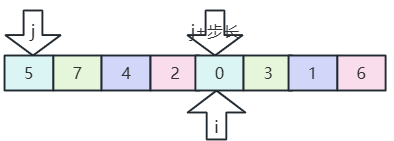
- 组内比较,排序:
- 5、0比较,交换位置;
- 7、3比较,交换位置;
- 4、1比较,交换位置;
- 2、6比较,位置不动;
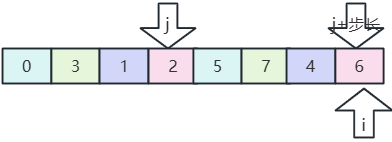
- 在分一半,步长为2;
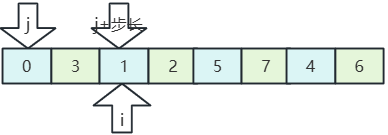
- 组内比较,排序(分组来回交替排序插入):
- 0、1比较,位置不动;
- 3、2比较,交换位置;
- 1、5比较,位置不动;
- 2、7比较,位置不动;
- 5、4比较,交换位置;
- 7、6比较,交换位置;
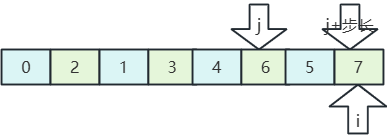
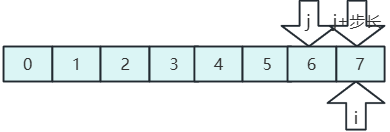
- 在分一半,步长为1,整个数组为一组;
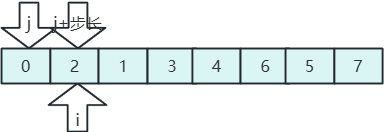
- 比较排序,直到结束,希尔排序完成。
时间复杂度:
| 轮数 | 间隔 | 交换次数 |
|---|---|---|
| 第一轮 | x/2=x/21x/2=x/2^1x/2=x/21 | x/2x/2x/2 |
| 第二轮 | x/2/2=x/22x/2/2=x/2^2x/2/2=x/22 | x/2x/2x/2 ~ x−1x-1x−1 |
| 第三轮 | x/2/2/2=x/23x/2/2/2=x/2^3x/2/2/2=x/23 | x/2x/2x/2 ~ x−1x-1x−1 |
| 第四轮 | x/2/2/2/2=x/24x/2/2/2/2=x/2^4x/2/2/2/2=x/24 | x/2x/2x/2 ~ x−1x-1x−1 |
| …… | …… | …… |
| 第k轮 | 1=x/2k1=x/2^k1=x/2k | x−1x-1x−1 |
得到关系式:1=x/2k1=x/2^k1=x/2k
转换:x=2kx=2^kx=2k
得到一个轮次的k与x的关系式是:k=logxk=logxk=logx
所有的轮次相加是:k=xlogxk=xlogxk=xlogx
得到时间复杂度是:O(nlogn)O(nlogn)O(nlogn)
java代码:
package com.xxx;import java.util.Arrays;//希尔排序
public class ShellSort {public static void main(String[] args) {int[] arr = {17,7,24,33,28,19,15,30};sort(arr);System.out.println(Arrays.toString(arr));}public static void sort(int[] arr) {//定义步长变量 grpfor(int grp=arr.length/2;grp>=1;grp=grp/2) {//定义游标 i,控制 i 的移动,组内进行插入排序for(int i=grp;i<arr.length;i++) {//结束 j 和 j+grp 完成组内的插入for(int j=i-grp;j>=0;j=j-grp) {// j 和 j+grp 指向的数据进行比较,交换if(arr[j]>arr[j+grp]) {int temp = arr[j];arr[j] = arr[j+grp];arr[j+grp] = temp;}else {break;}}}}}
}


》)






驱动开发)





![[muduo网络库]-muduo库TcpServer类解析](http://pic.xiahunao.cn/[muduo网络库]-muduo库TcpServer类解析)



)