子集

这道题求子集，集合的基本运算之一，按照高中数学学习集合的知识，可以把这个找幂集的过程按照元素的个数来划分步骤。也就是先找零个元素的子集，再找一个元素的子集，再找两个元素的子集...一直到找N个元素的集合为止。

我的第一想法是对找k个元素的集合这个过程使用回溯的方法。

回溯三部曲：

• 返回值void，参数startIndex
• 终止条件：找到n个数就可结束
• 当层函数逻辑循环
  • 横向循环：从startIndex开始往后依次遍历，作为当前轮的所有可能
  • 纵向迭代：startIndex层的数的下一个数作为迭代的下一层起点

代码(执行用时击败35.31%，消耗内存击败17.38%)：

class Solution {
vector<vector<int>> ans;
vector<int> path;
void backtrack(vector<int> nums,int len,int startIndex){if(path.size()==len){//终止条件ans.push_back(path);return;}for(int i = startIndex;i<nums.size();i++){//当前轮的循环path.push_back(nums[i]);backtrack(nums,len,i+1);//下一层的迭代path.pop_back();}
}
public:vector<vector<int>> subsets(vector<int>& nums) {for(int k = 0;k<=nums.size();k++){//子集元素的数量从0到|S|backtrack(nums,k,0);}return ans;}
};

感觉自己的时间和空间消耗还是比较糟糕，参考代码随想录的做法，发现原来可以不用这样划分子集的长度。因为求幂集的递归-回溯过程是宽度为集合长度，高度为集合长度的一棵树。如下图：

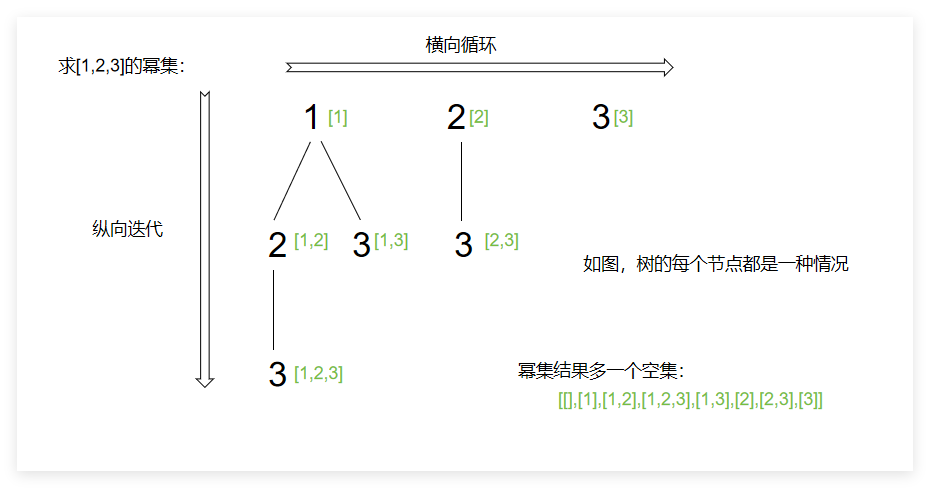
代码也省去对子集中元素个数的一一罗列，代码执行时间击败33.87%，消耗内存击败42.94%。竟然在时间消耗上更低了。

class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking(vector<int>& nums, int startIndex) {result.push_back(path); // 收集子集，要放在终止添加的上面，否则会漏掉自己if (startIndex >= nums.size()) { // 终止条件可以不加return;}for (int i = startIndex; i < nums.size(); i++) {path.push_back(nums[i]);backtracking(nums, i + 1);path.pop_back();}}
public:vector<vector<int>> subsets(vector<int>& nums) {result.clear();path.clear();backtracking(nums, 0);return result;}
};

这道题和之前的回溯不一样的地方在于，所有的树节点都是答案的一种情况，而之前的答案都是在叶子节点也就是满足终止条件的时候。求集合幂集的方法可以无需设置终止条件。

子集II

这道题是在上面第一道题基础上加上一个去重的操作，也就是第一次遇到元素时正常执行，但是第二次遇到相同的元素，则需要跳过。

代码如下：

class Solution {
vector<vector<int>> ans;
vector<int> path;
void backtrack(vector<int> nums,int startIndex){ans.push_back(path);//没有终止条件for(int i = startIndex;i<nums.size();i++){//当前层的循环if(i>startIndex && nums[i]==nums[i-1]){//不重复执行continue;}path.push_back(nums[i]);backtrack(nums,i+1);//递归调用下一层的函数path.pop_back();//回溯}
}
public:vector<vector<int>> subsetsWithDup(vector<int>& nums) {sort(nums.begin(),nums.end());//为了把集合中相同的元素集中到一起，需要排序backtrack(nums,0);return ans;}
};

写这一题代码的时候，我在for循环中使用continue，以为continue是直接从if跳到循环条件判断的地方，所以在continue前还加上了i++，导致我的代码过了给出的测试但没有AC。原来for循环中的contimue是跳转到i++这个循环变量递变的位置。