目录
引言:
G-C-D, Unlucky!
题意分析
逻辑梳理
代码实现
结语:
引言:
因为今天打了个ICPC网络赛,导致坐牢了一下午,没什么时间打题目了,就打了一道题,所以,今天我们就只讲一题了,该题是CF难度分值1400的题,今天应该是跟第一天一样轻松的训练量,那话不多说,我们进入题目讲解————>

G-C-D, Unlucky!
与先前一样。我们先来看题目
题意分析
这是题目的链接Problem - E - Codeforces
不想跳转的可以看下图

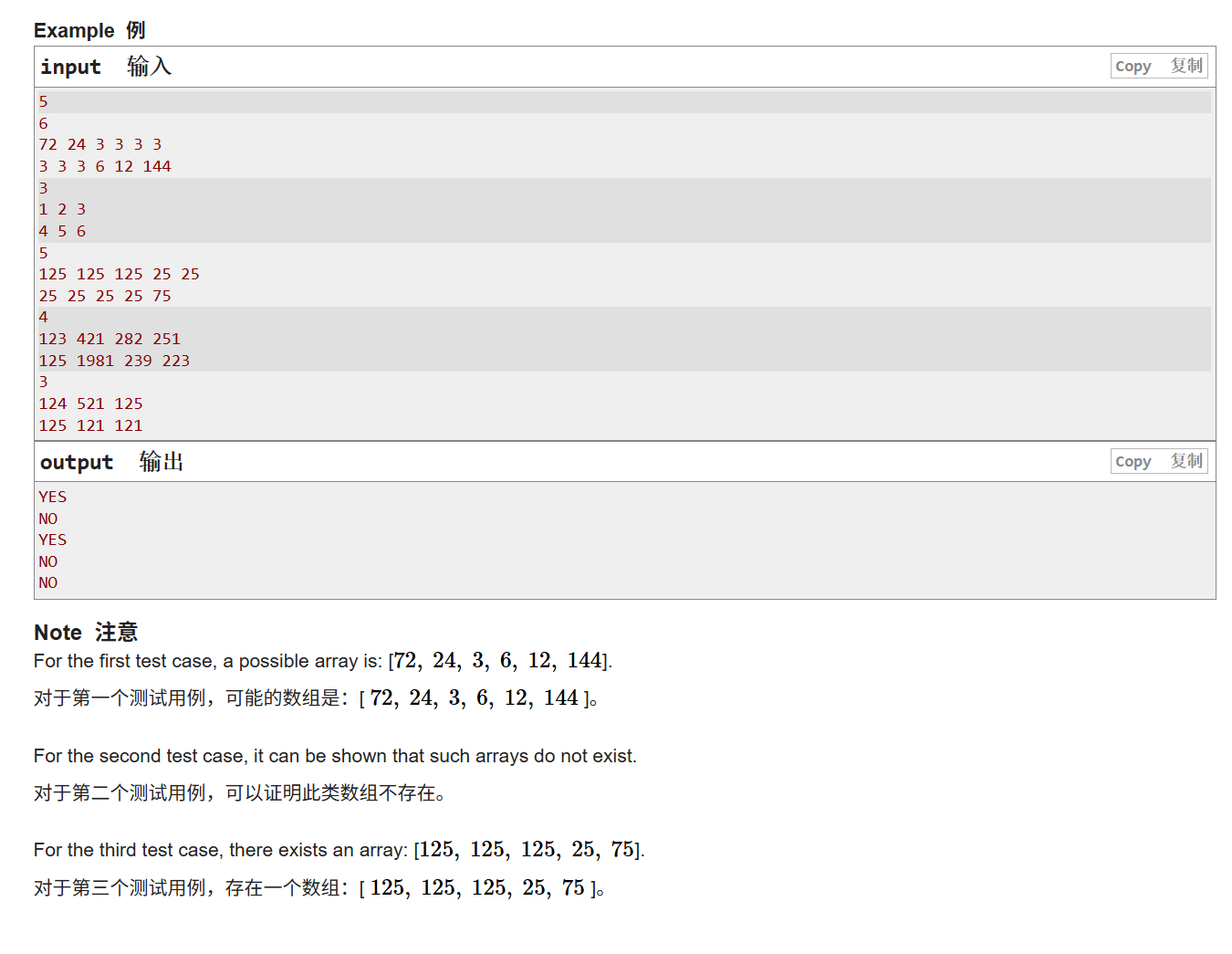
这个题目表达的意思其实是很简单的,就是输入2个数组,然后问是否存在一个数组a,满足,第一个数组是a数组从前往后求公约数,第二个数组是a数组从后往前求公约数,那么,题目意思就说完了,接下来我们来梳理一下逻辑
逻辑梳理
首先一个是从前往后依次公约数的数组,这个数组的第一个一定是a数组的首元素
还有一个是从后往前依次公约数的数组,这个数组的最后一个元素一定是a数组的尾元素
这个是第一眼就能看出的东西,但我感觉对这题没有什么用,但是,第一个数组的最后一个元素与第二个数组的首元素反而非常关键
因为第一个数组的末元素是将a数组全部进行求公约数,第二个数组的首元素是将a数组全部进行求公约数,只是一个是顺着求,一个是逆着求
所以,若这个a数组存在,那么第一个数组的末元素和第二个数组的首元素一定要相等,这是第一个若要让a数组存在需要满足的条件
那么,接下来,因为第一个数组是从前往后求公约数,所以第一个数组从前往后要单调不递增,因为第二个数组是从后往前求公约数,所以第二个数组从后往前要单调不递增,即从前往后要单调不递减,这是第二个若要让a数组存在需要满足的条件
然后,既然已经知道了数的变化顺序,接下来,我们来看变化规律,因为是一步步公约数求下去的,所以对第一个数组而言,i+1位置上的数肯定是i位置上数的因数或本身而不能是其他的数,若是其他的数就不满足依次求公约数的性质了
对第二个数组也同理,只是第二个数组是从后往前求公约数,所以i位置上的数肯定是i+1位置上的数的因数或者他本身而不能是其他的数
上边的便是第三个若要让a数组存在需要满满足的条件,即第一个数组依次往后的数据要是他前一个数据的因数或本身,第二个数组依次往前的数据要是他后一个数据的因数或本身
还有一个就比较抽象了,这也是最难想的一个条件,这个条件我也想了好久,这个条件如图
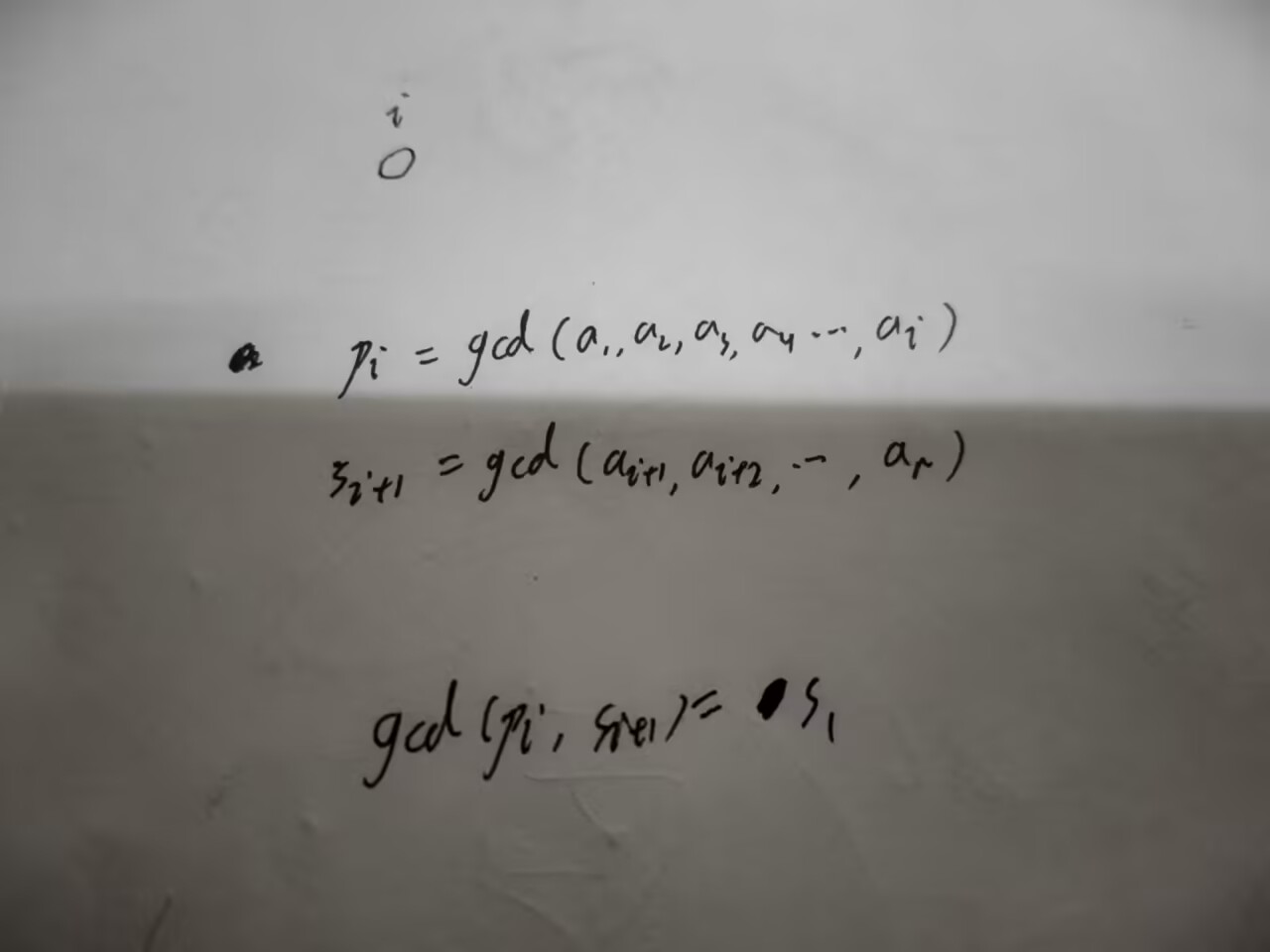
我们只需要通过一个循环求 下标为i的第一个数组的元素 和 下标为i+1的第二个数组的元素 的最大公约数求出来判断是否为第二个数组的第一个元素即可(因为这俩个元素求出来的公约数就是整个数组的公约数了)
那么,四个关键的条件就集齐啦,接下来我们就进入代码实现的环节
代码实现
逻辑已经讲完了,接下来我们只需要用代码将四个功能实现出来就可以了,那么具体我就不多讲了,直接放AC码啦
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <queue>
#include <vector>
using namespace std;int t;
long long a[100010];
long long b[100010];long long gcd(long long x, long long y)
{if (y == 0)return x;return gcd(y, x % y);
}void solve()
{int xixi = 0;int n;cin >> n;a[0] = 1e10;for (int i = 1; i <= n; i++){cin >> a[i];if (a[i] > a[i - 1])xixi = 1;}for (int i = 1; i <= n; i++){cin >> b[i];if (b[i] < b[i - 1])xixi = 1;}for (int i = 1; i < n; i++){if (a[i] % a[i + 1] || b[i + 1] % b[i]){xixi = 1;break;}if (gcd(a[i], b[i+1]) != b[1]){xixi = 1;break;}}if (n == 1 && a[1] == b[1]){cout << "Yes" << endl;return;}if (xixi || a[n] != b[1]){cout << "No" << endl;return;}cout << "Yes" << endl;
}int main()
{cin >> t;while (t--){solve();}return 0;
}那么这道题就讲完啦
结语:
今日算法讲解到此结束啦,希望对你们有所帮助,谢谢观看,如果觉得不错可以分享给朋友哟









)



)





