欢迎关注[【AIGC论文精读】](https://blog.csdn.net/youcans/category_12321605.html）原创作品
【DeepSeek论文精读】1. 从 DeepSeek LLM 到 DeepSeek R1
【DeepSeek论文精读】10. DeepSeek-Coder-V2: 突破闭源模型在代码智能领域的障碍
【DeepSeek论文精读】12. DeepSeek-Prover-V2: 通过强化学习实现子目标分解的形式化数学推理

0. DeepSeek-Prover-V2 模型介绍

DeepSeek-Prover-V2 是由 DeepSeek 团队开发的开源大型语言模型，专注于形式化数学定理证明，尤其在 Lean 4 平台上的表现达到行业领先水平。该模型通过结合非形式化推理与形式化验证，实现了数学直觉与符号逻辑的双向对齐，标志着AI在数学推理领域的重大突破。

0.1 模型概述

参数规模与架构

• 双版本发布：包含 DeepSeek-Prover-V2-671B（6710亿参数）和 DeepSeek-Prover-V2-7B（70亿参数）两个版本。前者基于DeepSeek-V3架构，采用混合专家系统（MoE），每层包含256个路由专家和1个共享专家，支持超长上下文（最长163,840 tokens）和多精度计算（如FP8量化）1510。

• 专精数学推理：不同于通用对话模型，其设计目标聚焦于形式化定理证明，生成兼容Lean 4的严谨证明步骤，适用于自动验证、教学辅助及数学发现等场景14。

核心创新

• 递归定理证明流程：通过DeepSeek-V3模型将复杂问题分解为子目标（subgoals），生成自然语言证明草图和Lean 4形式化框架，再通过7B模型递归解决子目标并合成完整证明。

• 冷启动数据生成：结合非形式化的思维链（CoT）与形式化证明步骤，生成高质量的初始训练数据，为强化学习提供基础。

0.2 关键技术

训练流程

• 冷启动阶段：利用DeepSeek-V3分解问题并生成子目标，通过7B模型解决子目标后，将证明与CoT结合，形成初始训练数据。

• 强化学习优化：采用 GRPO算法（群体相对策略优化），以二元奖励（正确为1，错误为0）驱动模型优化，增强形式化证明与初始推理的一致性。

• 两阶段训练：

  • 非CoT模式：快速生成简洁的Lean代码，提升响应效率。

  • CoT模式：通过结构化思维链和强化学习，提升逻辑严谨性。

课程学习与数据增强

• 通过子目标生成不同难度的定理，逐步增加训练任务复杂度，引导模型学习复杂证明。

• 筛选7B模型无法端到端解决但子目标已证明的问题，构建合成数据以增强泛化能力。

0.3 性能表现

• 基准测试成绩

  • MiniF2F-test：通过率高达88.9%（Pass@8192），创下神经定理证明领域的新纪录。

  • PutnamBench：解决658个问题中的49个，展现大学水平数学问题的处理能力。

  • AIME竞赛题：在15道高中竞赛级题目中解决6道，而通用模型DeepSeek-V3通过多数表决解决8道，显示形式化与非形式化推理差距显著缩小。

• 扩展评估

  • ProverBench数据集：包含325个形式化问题，涵盖高中竞赛（如AIME 24-25）和本科数学（如线性代数、微积分），为多样化场景评估提供标准。

  • 跨领域泛化：在组合数学基准CombiBench中解决12/77问题，展示跨学科潜力。

DeepSeek-Prover-V2通过创新的子目标分解与强化学习策略，成功弥合了非形式化推理与形式化验证的鸿沟，成为数学AI领域的标杆。其高性能与开源特性为学术界和工业界提供了强大工具，未来或可扩展至国际数学奥林匹克（IMO）级别问题的挑战。

0.4 论文简介

• 论文标题：DeepSeek-Prover-V2: Advancing Formal Mathematical Reasoning via Reinforcement Learning for Subgoal Decomposition（DeepSeek-Prover-V2: 通过强化学习实现子目标分解的形式化数学推理）
• 发布时间：2025 年 4 月
• 论文作者：Z.Ren, ZhihongShao, JunxiaoSong, HuajianXin, et al.
• 下载地址：arxiv: Deepseek-Prover-V2
  Hugging Face：https://huggingface.co/deepseek-ai/DeepSeek-Prover-V2-671B
  GitHub：https://github.com/deepseek-ai/DeepSeek-Prover-V2/tree/main


0.5 摘要

我们介绍DeepSeek-Prover-V2，这是一个专为Lean 4形式化定理证明设计的开源大型语言模型，其初始化数据通过由DeepSeek-V3驱动的递归定理证明流程收集。冷启动训练流程首先提示DeepSeek-V3将复杂问题分解为一系列子目标。已解决子目标的证明被合成为思维链过程，与DeepSeek-V3的逐步推理相结合，为强化学习创建初始冷启动。该流程使我们能够将非形式化和形式化数学推理整合到统一模型中。

最终模型DeepSeek-Prover-V2-671B在神经定理证明中实现最先进性能，达到MiniF2F-test 88.9%的通过率，并解决了PutnamBench 658个问题中的49个。除标准基准测试外，我们引入ProverBench（包含325个形式化问题的集合）以丰富评估体系，包括从近期AIME竞赛（第24-25届）精选的15个问题。针对这15个AIME问题的进一步评估显示，模型成功解决了其中6个。相比之下，DeepSeek-V3通过多数表决方法解决了其中8个问题，这表明大型语言模型中形式化与非形式化数学推理之间的差距正在显著缩小。

1. 引言

大型语言模型 （LLM） 中推理能力的出现彻底改变了人工智能的许多领域，尤其是在数学问题解决领域 （DeepSeek-AI，2025 年）。 这些进步在很大程度上是由推理时间缩放的范式实现的，最明显的是通过自然语言思维链推理 （Jaech et al., 2024）。LLM 不是仅仅依靠一次向前传递来得出答案，而是可以反思中间推理步骤，从而提高准确性和可解释性。尽管自然语言推理在解决竞赛级别的数学问题方面取得了成功，但它在形式定理证明中的应用仍然具有根本的挑战性。LLM 以本质上非形式化化的方式执行自然语言推理，依赖于启发式、近似和数据驱动的猜测模式，这些模式通常缺乏形式化化验证系统所需的严格结构。相比之下，Lean （Moura and Ullrich， 2021）、Isabelle （Paulson， 1994） 和 Coq （Barras et al., 1999） 等证明助手在严格的逻辑基础上运行，其中每个证明步骤都必须明确构建和形式验证。这些系统不允许歧义、隐含的假设或遗漏细节。弥合非形式化化、高级推理和形式验证系统的句法严谨性之间的差距仍然是神经定理证明的一个长期研究挑战 （Yang et al., 2024）。

为了利用非形式化化数学推理的优势来支持形式定理证明，一种经典方法是在自然语言证明草图的指导下分层分解形式证明。（Jiang et al. 2023） 提出了一个称为草稿、草图和证明 （DSP） 的框架，该框架利用大型语言模型以自然语言生成证明草图，然后将其转换为形式化化的证明步骤。这种非形式化化到形式化化的定理证明范式与分层强化学习中的子目标概念密切相关 （Barto 和 Mahadevan，2003 年; Nachum 等 人，2018 年;Eppe et al., 2022）， 其中复杂的任务被分解为更简单的子任务层次结构，这些子任务可以独立解决以逐步实现总体目标。在形式化化定理证明中，子目标通常是有助于证明更大定理的中间命题或引理 （Zhao et al., 2023， 2024）。 这种分层分解与人类解决问题的策略保持一致，并支持模块化、可重用性和更高效的证明搜索 （Wang et al., 2024b;Zheng et al., 2024） 的最近的研究通过采用多层层次结构来生成结构化证明 （Wang et al., 2024a）， 并利用强化学习技术将复杂定理优化为可管理的子目标 （Dong et al., 2024）， 从而扩展了这种范式。

在本文中，我们开发了一个用于子目标分解的推理模型，利用一套合成冷启动数据和大规模强化学习来提高其性能。 为了构建冷启动数据集，我们开发了一个简单而有效的递归定理证明管道，利用 DeepSeek-V3 （DeepSeek-AI， 2024） 作为子目标分解和形式化化的统一工具。我们提示 DeepSeek-V3 将定理分解为高级证明草图，同时在 Lean 4 中将这些证明步骤形式化化，从而产生一系列子目标。由于子目标分解由大型通用模型提供支持，因此我们使用较小的 7B 模型来处理每个子目标的证明搜索，从而减少相关的计算负担。此外，我们引入了一个课程学习框架，该框架利用分解的子目标生成猜想定理，逐步增加训练任务的难度，以更好地指导模型的学习过程。一旦解决了具有挑战性的问题的分解步骤，我们将完整的分步形式证明与 DeepSeek-V3 中的相应思路配对，以创建冷启动推理数据。在冷启动的基础上，应用后续的强化学习阶段，以进一步加强非形式化化数学推理和形式证明构造之间的联系。我们的实验表明，在任务分解中，从非形式化化推理的冷启动开始的强化学习显著提高了模型的形式定理证明能力。由此产生的 DeepSeek-Prover-V2-671B 模型在多个基准测试中建立了最先进的神经定理证明。在 MiniF2F 测试中，它达到 82.4% Pass@32 的准确性，提高到 88.9% Pass@8192。 该模型显示出对大学水平定理证明的强大泛化能力，使用 Pass@1024 解决
37.1% ProofNet 测试问题，并解决 658 个具有挑战性的 PutnamBench 问题中的 49 个。此外，我们还贡献了 ProverBench，这是一个包含 325 个形式化化问题的基准数据集，以推进神经定理证明研究，其中包括来自著名的 AIME 竞赛（24-25 岁）的 15 个问题。DeepSeek-Prover-V2-671B 成功解决了这 15 个具有挑战性的 AIME 问题中的 6 个，进一步展示了其复杂的数学推理能力。

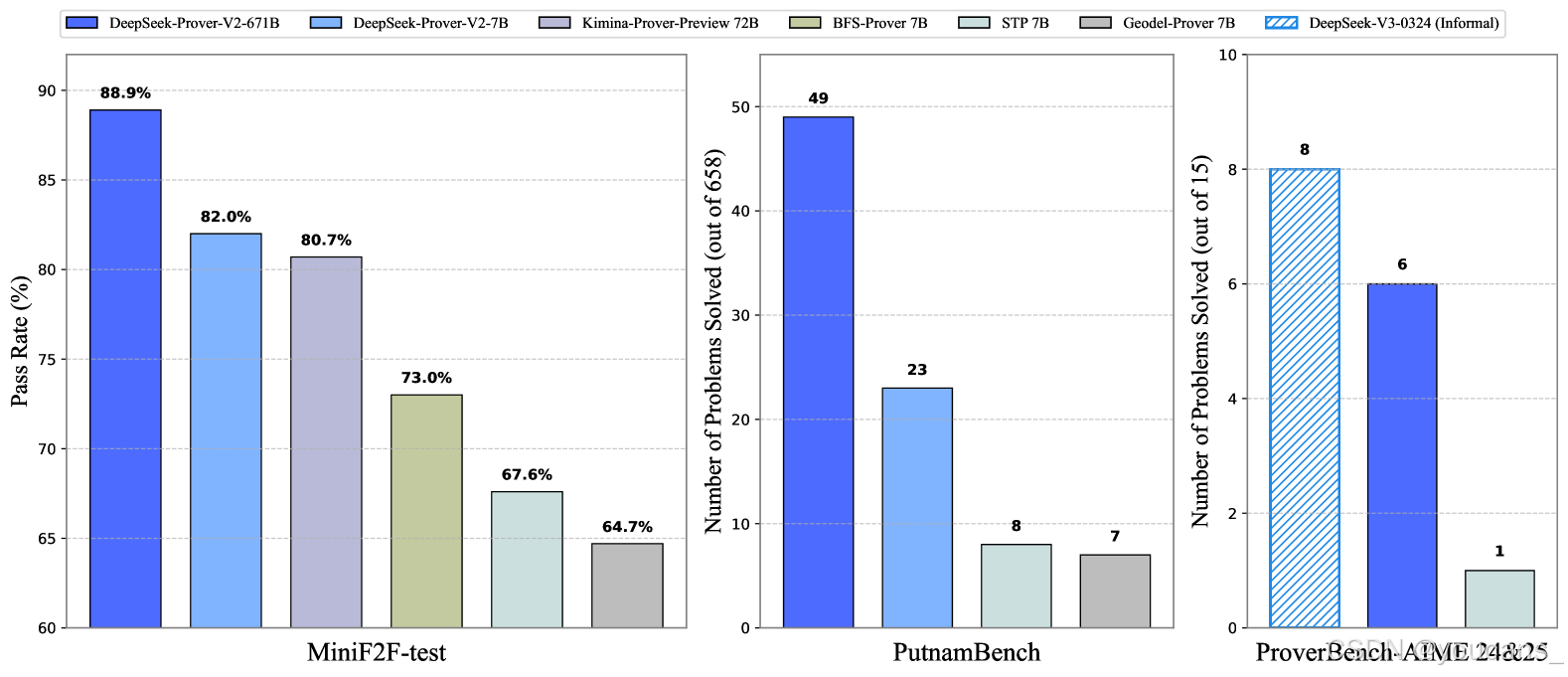
图 1：DeepSeek-Prover-V2 的基准测试性能。在 AIME 基准测试中，DeepSeek-V3 使用用于自然语言推理的标准查找-答案任务进行评估，而证明者模型生成精益代码，为给定的正确答案构建形式证明。

图 2：DeepSeek-Prover-V2 采用的冷启动数据收集过程概述。
我们首先提示 DeepSeek-V3 生成自然语言的证明草图，同时将其形式化化为精益声明，并为遗漏的证明细节添加占位符。然后，一个 7B 证明器模型递归地求解分解的子目标。通过组合这些子目标证明，我们为原始复杂问题构建了一个完整的形式化化证明。这个组合证明被附加到 DeepSeek-V3 的原始思维链中，为形式化化的数学推理创建高质量的冷启动训练数据。

2. 方法

2.1 通过子目标分解进行递归证明搜索

将复杂定理的证明分解为一系列较小的引理，作为垫脚石是人类数学家通常采用的有效策略。先前的几项研究在神经定理证明的背景下探索了这种分层策略，旨在通过利用现代 LLM 的非形式化化推理能力来提高证明搜索效率 （Jiang et al., 2023;Zhao et al., 2023;Wang et al., 2024a;Dong et al., 2024） 的在本文中，我们开发了一个简单而有效的管道，它利用 DeepSeek-V3 （DeepSeek-AI, 2024） 作为形式定理证明中子目标分解的统一工具。

从自然语言推理中绘制形式证明草图

大型语言模型的最新进展导致了非形式化化推理能力的重大突破。为了弥合形式化化和非形式化化推理之间的差距，我们利用尖端的通用 LLM，以其强大的数学推理和指令跟踪能力而闻名，来构建我们定理证明系统的基础框架。我们的研究结果表明，现成的模型，如 DeepSeek-V3 （DeepSeek-AI， 2024）， 能够分解证明步骤并用形式语言表达它们。为了证明给定的形式化化定理陈述，我们提示 DeepSeek-V3 首先用自然语言分析数学问题，然后将证明分解为更小的步骤，将每个步骤转换为相应的精益形式化化陈述。由于众所周知，通用模型难以生成完整的精益证明，因此我们指示 DeepSeek-V3 仅生成省略细节的高级证明草图。由此产生的思路链最终形成一个精益定理，该定理由一系列陈述组成，每个陈述都以一个令人遗憾的占位符结束，表示要解决的子目标。这种方法反映了人类的证明构造风格，其中复杂定理逐渐简化为一系列更易于管理的引理。

图 3： 我们如何将分解的子目标转换为一系列引理语句的说明性示例。我们首先 （a） 替换原始目标状态，然后 （b） 将前面的子目标作为前提。语句类型 （b） 用于递归解决复杂问题，而类型 （a） 和 （b） 都被纳入课程学习过程。

子目标的递归解析

利用 DeepSeek-V3 生成的子目标，我们采用递归求解策略来系统地解决每个中间证明步骤。我们从语句中提取子目标表达式，以替换给定问题中的原始目标（见图 3（a）），然后将前面的子目标作为前提（见图 3（b））。这种构造使得后续的子目标能够使用早期步骤的中间结果来解决，从而促进更本地化的依赖结构，并促进更简单词元的开发。为了减少大量证明搜索的计算开销，我们采用了一个更小的 7B 证明器模型，专门针对处理分解的引理进行了优化。在成功求解所有分解步骤后，可以自动推导出原始定理的完整证明。

基于子目标的定理证明的课程学习。

证明模型的训练需要大量的形式化化语言问题集，通常是通过形式化化现有的自然语言数学语料库得出的（Xin et al., 2024a;Ying et al., 2024;Lin et al., 2025） 的尽管人工创作的文本的形式化化提供了高质量和多样化的形式化化内容，但证明者模型的结果训练信号通常很少，因为很大一部分计算尝试没有产生成功的证明，因此没有提供积极的奖励信号。为了生成更密集的训练信号，Dong 和 马 （2025） 提出了一种自游戏方法，通过生成与原始定理陈述密切相关的可处理猜想来丰富训练问题集，从而更有效地使用训练计算。在本文中，我们实现了一种简单的方法，利用子目标来扩展用于模型训练的形式化化语句的范围。我们生成了两种类型的子目标定理，一种将前面的子目标作为前提，另一种没有，分别对应于图 3（b） 和图 3（a）。这两种类型都被整合到专家迭代阶段 （Polu 和 Sutskever，2020 年）， 建立了一个课程，逐步指导证明者模型系统地解决精心策划的挑战性问题子集。该程序建立在与 AlphaProof 的测试时强化学习 （DeepMind，2024 年） 相同的基本原理之上，其中生成目标问题的变化以增强模型解决具有挑战性的 IMO 级问题的能力。

2.2 元统一非形式化化推理和证明形式化化

上面讨论的算法框架分两个阶段运行，利用两个互补的模型：DeepSeek-V3 用于引理分解，7B 证明模型用于完成相应的形式化化证明细节。该管道通过将语言模型的高级推理与精确的形式验证相结合，为合成形式推理数据提供了一种自然且可扩展的机制。通过这种方式，我们将非形式化化数学推理和证明形式化化的能力统一在一个模型中。

通过合成数据进行冷启动。

我们以端到端的方式策划了 7B 证明器模型仍未解决的具有挑战性的问题子集，但所有分解的子目标都已成功解决。通过组合所有子目标的证明，我们为原始问题构建了一个完整的形式证明。然后将此证明附加到 DeepSeek-V3 的思维链中，该思维链概述了相应的引理分解，从而产生了非形式化化推理和随后的形式化化的内聚综合。它支持收集数百个高质量的合成冷启动数据，这些数据作为训练 DeepSeek-Prover-V2 的基础。这种冷启动数据集生成策略不同于 Kimina-Prover （Wang et al., 2025） 的策略，后者是形式推理模型的同步工作。具体来说，我们通过将自然语言证明直接形式化化为结构化的形式化化证明草图来合成数据。相比之下，Kimina-Prover 采用了相反的工作流程：它首先收集完整的形式化化证明以及非形式化化的证明，然后使用通用推理模型将中间自然语言推理步骤逆向合成为连贯的思维块。

面向推理的强化学习。

在合成冷启动数据上微调证明者模型后，我们执行强化学习阶段，以进一步增强其将非形式化化推理与形式证明构建联系起来的能力。遵循推理模型的标准训练目标 （DeepSeek-AI， 2025）， 我们使用二进制正确或错误的反馈作为奖励监督的主要形式。在训练过程中，我们观察到生成的证明的结构经常与思维链指导提供的引理分解不同。为了解决这个问题，我们在训练的早期步骤中加入了一致性奖励，它惩罚了结构错位，明确强制在最终证明中包含所有分解的结构化引理。在实践中，强制执行这种对齐可以提高证明的准确性，尤其是在需要多步推理的复杂定理上。

2.3 DeepSeek-Prover-V2 的训练详情

两阶段训练。

DeepSeek-Prover-V2 是通过一个两阶段的训练管道开发的，该管道建立了两种互补的证明生成模式：

1. 高效非思维链 （non-CoT） 模式：该模式针对形式化化精益证明代码的快速生成进行了优化，专注于生成简洁的证明，没有明确的中间推理步骤。

2. 高精度思维链 （CoT） 模式：该模式系统地阐明中间推理步骤，强调透明度和逻辑进展，然后构建最终的形式证明。

与 DeepSeek-Prover-V1.5 （Xin et al., 2024b） 一致，这两种生成模式由两个不同的引导提示控制（示例见附录 A）。在第一阶段，我们在课程学习框架内采用专家迭代来训练非 CoT 证明者模型，同时通过基于子目标的递归证明来综合难题的证明。选择非 CoT 生成模式是为了加速迭代训练和数据收集过程，因为它提供了明显更快的推理和验证周期。在此基础上，第二阶段利用了通过将 DeepSeek-V3 的复杂数学推理模式与我们的合成形式证明集成而合成的冷启动思维链 （CoT） 数据。CoT 模式通过进一步的强化学习阶段得到增强，遵循通常用于推理模型的标准训练管道。

专家迭代。

DeepSeek-Prover-V2 的非 CoT 模式的训练程序遵循专家迭代的范式 （Polu 和 Sutskever，2020）， 这是一个广泛采用的开发形式定理证明器的框架。在每次训练迭代中，当前最佳证明者策略用于为那些在先前迭代中仍未解决的具有挑战性的问题生成证明尝试。这些成功的尝试由 Lean proof Assistant 验证，将被合并到 SFT 数据集中，以训练改进的模型。这种迭代循环确保模型不仅从初始演示数据集中学习，而且还提取出自己的成功推理轨迹，逐步完善其解决更难问题的能力。整体训练程序与 DeepSeek-Prover-V1 （Xin et al., 2024a） 和 DeepSeek-Prover-V1.5 （Xin et al., 2024b） 基本一致，训练题的分布只有两处修改。首先，我们整合了来自自形式化化和各种开源数据集的其他问题 （Ying et al., 2024;董和马，2025 年;Lin et al., 2025） 的研究中进行了研究，扩大了训练问题领域的覆盖范围。其次，我们用子目标分解产生的问题来增强数据集，旨在解决 MiniF2F 基准的有效拆分中更具挑战性的实例 （Zheng et al., 2022）。

监督微调。

我们在 DeepSeek-V3-Base-671B （DeepSeek-AI， 2024） 上执行监督微调，在 16,384 个标记的上下文窗口内使用 5e-6 的恒定学习率。我们的训练语料库由两个互补来源组成：（1） 通过专家迭代收集的非 CoT 数据，无需中间推理步骤即可生成精益代码;（2） 第 2.2 节 中描述的冷启动 CoT 数据，它将 DeepSeek-V3 的高级数学推理过程提炼成结构化的证明路径。非 CoT 组件强调精益定理证明器生态系统中的形式验证技能，而 CoT 示例明确模拟了将数学直觉转化为形式证明结构的认知过程。

强化学习。

我们采用集团相对策略优化 （GRPO;Shao et al., 2024） 作为我们的强化学习算法，该算法在推理任务中表现出卓越的有效性和效率 （DeepSeek-AI，2025）。 与 PPO （Schulman et al., 2017） 不同，GRPO 通过为每个定理提示对一组候选证明进行采样并根据它们的相对奖励优化策略，消除了对单独批评模型的需求。训练利用二元奖励，其中每个生成的 Lean 证明在验证正确时获得 1 的奖励，否则获得 0 的奖励。为了确保有效的学习，我们策划了训练提示，以仅包含具有足够挑战性但可以通过监督微调模型解决的问题。在每次迭代期间，我们对 256 个不同的问题进行采样，每个定理生成 32 个候选证明，最大序列长度为 32,768 个标记。

蒸馏。

我们将 DeepSeek-Prover-V1.5-Base-7B （Xin et al., 2024b） 的最大上下文长度从 4,096 个标记扩展到 32,768 个标记，并使用在 DeepSeek-Prover-V2-671B 的强化学习阶段收集的推出数据微调这个扩展上下文模型。除了 CoT 推理模式外，我们还整合了在专家迭代期间收集的非 CoT 证明数据，以实现一种经济高效的证明选项，从而使用小规模模型生成简洁的形式化化输出。此外，我们执行了与 671B 模型训练中使用的相同强化学习阶段，以提高 DeepSeek-Prover-V2-7B 的性能。

3. 试验结果

在本节中，我们介绍了 DeepSeek-Prover-V2 在形式定理证明的各种基准数据集中的系统评估，涵盖高中竞赛问题和本科阶段的数学。DeepSeek-Prover-V2 的所有实验结果均使用 Lean 4.9.0 进行，使用与 DeepSeek-Prover-V1.5 相同的测试环境 （Xin et al., 2024b）。 无需进一步说明，基线评估结果来源于各自的原始论文。

3.1 MiniF2F 基准测试的结果

MiniF2F

MiniF2F（Zheng et al., 2022） 由 488 个形式化化的问题陈述组成，这些问题陈述来自各种数学材料，包括 AIME、AMC 和 IMO 竞赛，以及来自 MATH 数据集的选定问题 （Hendrycks et al., 2021）。 该基准测试包括涵盖初等数学核心领域的奥林匹克级别问题，包括代数、数论和归纳。这些问题被分为两个大小相等的子集，分别用 miniF2F-valid 和 miniF2F-test 表示，每个子集包含 244 个问题，在主题领域中分布相同。我们保留 miniF2F 测试集专门用于评估模型性能，而 miniF2F 有效问题通过子目标分解被纳入课程学习。我们采用了 Wang 等 人（2025 年） 发布的 miniF2F 修订版，并进一步引入了 miniF2F-valid 的另外两个版本和 miniF2F-test 的一个版本（见附录 C）。

与 SoTA 模型的比较。

表1总结了在miniF2F-test数据集上评估的最新形式定理证明模型的对比情况。实验结果表明，DeepSeek-Prover-V2-671B 在miniF2F-test基准测试中建立了新的最佳性能，仅利用32个样本便实现了前所未有的82.4%的准确率，同时采用CoT生成策略。值得注意的是，参数效率更高的DeepSeek-Prover-V2-7B 也表现出竞争性的性能，超越了文献中所有现有的开源定理证明器。进一步的比较分析揭示了一个引人注目的扩展模式：随着样本预算从1增加到8192，7B和671B变体之间的性能差距显著扩大，较大的模型显示出了更好的样本效率和更陡峭的改进趋势。

表 1：与 miniF2F-test 数据集上的最新模型对比。
符号 𝜇 ± 𝜎 表示平均准确率 𝜇 和标准差 𝜎。标签 CoT 和 non-CoT 分别指代统一模型的两种生成模式，每种模式由不同的提示引导。

通过子目标引导的课程来证明具有挑战性的问题。

表2 详细列出了DeepSeek-Prover-V2在miniF2F基准测试中解决的问题，它在验证集上以91.0%的正确率和测试集上以88.9%的正确率实现了强整体性能。值得注意的是，我们所采用的子目标引导的课程学习框架，该框架将通用模型DeepSeek-V3与轻量级专门7B证明器相结合，实现了miniF2F-valid上90.2%的成功率，几乎与DeepSeek-Prover-V2-671B的性能相匹配。这些发现突显了当前最先进的通用LLM不仅能够超越自然语言理解，还能够在支持复杂形式推理任务方面发挥有效作用。通过战略性地分解子目标，模型能够将具有挑战性的问题分解为一系列可处理的步骤，从而在非形式推理和形式证明构建之间架起一座有效桥梁。

表2: DeepSeek-Prover-V2-671B 在miniF2F基准测试中解决的问题。
miniF2F-valid上的结果是在课程学习过程中收集的，而对剩余的问题，则进一步使用Pass@8192调用DeepSeek-Prover-V2-671B。

基于推理 vs. 不基于推理。

表1中的实验结果表明，在形式数学推理方面，基于推理的推理模式在性能上远超无基于推理模式。这进一步证实了基于推理（CoT）提示的有效性，这种提示鼓励将复杂问题分解为中间步骤，并进一步确认了推理时间缩放在形式定理证明领域中的有效性。补充这些发现，表3提供了DeepSeek-Prover-V2在不同推理模式下生成的令牌数量统计数据。正如预期的那样，基于推理模式生成了显著更长的输出，反映出其复杂的推理过程。有趣的是，在无基于推理模式下，671B模型平均生成的输出比7B模型更长。进一步检查发现，虽然在无基于推理模式下没有提示显式的推理，但较大的模型往往在证明代码中插入了一些类似于隐式推理步骤的简要自然语言注释（见附录A）。这表明高容量模型即使在没有显式的基于推理提示的情况下，也可能隐式地内化并外化中间的推理过程。

表3：DeepSeek-Prover-V2 在 miniF2F-test 上生成的平均 Token 数量

3.2. 学士学位水平基准测试

ProofNet（Azerbayev等人，2023）包含371个问题，均基于Lean 3语言，这些问题来自各种流行的本科纯数学教科书，涵盖了实分析、复分析、线性代数、抽象代数和拓扑学等主题。我们使用Xin等人（2024b）提供的ProofNet的Lean 4翻译版本，该版本进一步分为两个部分：ProofNet-valid和ProofNet-test，分别包含185和186个问题。ProofNet的测试集专门用于模型评估，因为ProofNet-valid问题的变体包括在Dong和Ma（2025）提供的公共合成数据集中，该数据集用于我们的监督微调。如表4所示，与无基于推理（non-CoT）设置相比，使用基于推理（CoT）推理时DeepSeek-Prover-V2的通过率显著提高。值得注意的是，尽管训练数据主要来自高中水平的数学，该模型仍能很好地泛化到更高级的本科数学问题，这突显了其强大的形式推理能力。

PutnamBench

PutnamBench（Tsoukalas等人，2024）是一个不断更新的基准工具，包含从1962年至2023年的威廉·洛厄尔·普特南数学竞赛中的竞赛数学问题。普特南竞赛是一个高度 prestigio 的年度数学竞赛，面向美国和加拿大大学本科生，涵盖分析、线性代数、抽象代数、组合数学、概率和集合论等多个大学水平的领域。我们评估了最新版本的PutnamBench，其中包含658个形式化化在Lean 4中的问题。排除与Lean 4.9.0不兼容的问题后，我们评估了剩余的649个问题。如表4所示，DeepSeek-Prover-V2-671B 在PutnamBench 中显示出增强的推理能力，解决了49个问题，并显著领先于其非基于推理（non-CoT）的版本。这些结果进一步突显了基于推理（CoT）推理方法在处理有挑战性的本科数学问题上的有效性。

表 4：ProofNet-test 和 PutnamBench 上的实验结果。
PutnamBench 上 Goedel-Prover-SFT 和 STP 的分数来自他们的原始论文，该论文对包含 644 个问题的早期版本的 PutnamBench 进行了评估。

通过强化学习实现技能发现。

我们在评估中一个出乎意料的发现是，DeepSeek-Prover-V2-7B 在非基于推理（non-CoT）生成模式下在PutnamBench数据集中表现出色。值得注意的是，这个较小的7B模型成功解决了普特南Bench-671B未能解决的13个问题，使我们在普特南Bench中解决的问题总数从49个增加到62个，占658个总问题的百分比。经过仔细检查模型的输出，我们发现7B模型推理方法中的一种独特模式：7B模型频繁使用Cardinal.toNat和Cardinal.natCast_inj 来处理涉及有限基数的问题（见附录B中的例子），而在671B版本生成的输出中这些特定的技术几乎是不存在的。这种方法似乎使模型能够有效解决需要精妙操作基数值的问题的子集。

3.3 组合问题的结果

CombiBench

CombiBench（Liu等人，2025）是一个全面的基准工具，包含100个形式化化在Lean 4中的组合数学竞赛问题，每个问题都配有相应的自然语言陈述。我们评估了DeepSeek-Prover-V2 在此基准中的有解设置，其中正确答案嵌入在Lean陈述中，使得评估主要集中在证明生成上。在过滤掉与Lean 4.9.0不兼容的问题以及包含多个“sorry”占位符的问题后，我们在基准中评估了77个问题，并成功解决了其中12个。这些结果表明，尽管证明模型主要是在数论和代数领域进行训练的，但它在组合问题上展现出了令人鼓舞的泛化能力，尽管这类问题仍具持续的挑战性。

3.4 ProverBench：AIME和教科书问题的形式化化

为了增强现有的基准并推进形式化化定理证明的研究，我们引入了一个包含325个问题的基准数据集。其中，15个问题是从最近的AIME竞赛（AIME 24和25）中的数论和代数题目形式化化而来的，提供了真实的高中竞赛级别挑战。剩余的310个问题则来自精心挑选的教科书范例和教育教程，贡献了一个多样化且具有教学基础的形式化化数学问题集合。此基准旨在能够对高中竞赛问题和大学级别数学进行全面评估。


AIME 形式化化。

美国邀请数学考试（AIME）是一项每年举行的数学竞赛，旨在挑战和表彰在数学表现出卓越能力的才华横溢的高中学生。AIME 24 和 25 的题目已成为评估大型语言模型推理能力的标准基准。

为了弥合形式化化和非形式化化数学推理评估之间的差距，我们从 AIME 24 和 25 中精心挑选并形式化化了一部分问题。为了确保形式化化更简洁，我们过滤掉了几何、组合和计数问题，这些问题是 Lean 中难以处理的。这最终筛选出了 15 个选定问题，涵盖了初等数论和代数的竞赛级别主题。我们使用标准的“找答案”任务来评估 DeepSeek-V3-0324 在自然语言数学推理方面的性能。通过对 16 个抽样响应进行多数投票，模型成功解决了 8 个问题。相比之下，DeepSeek-Prover-V2-671B 在给定正确答案的形式化化证明生成设置下，能够为 6 个问题构建有效的形式证明。这一对比表明，非形式化化数学推理与形式化化定理证明之间的性能差距正在显著缩小，显示出高级语言模型在语言理解与形式逻辑 rigor 方面的逐步趋同。

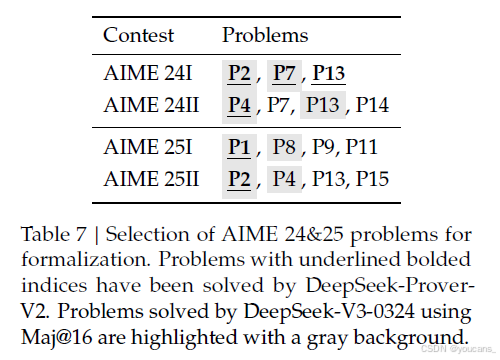
教科书形式化化。

除了 AIME 24 和 25 题目外，我们还从用于高中竞赛和本科课程的教科书中精心挑选了一些题目，以加强特定数学领域的内容覆盖面。这一筛选过程确保了从易到难、从具体主题到广泛领域的全面代表性。因此，我们形式化化了 310 个问题，涵盖了广泛的领域，从竞赛水平的初等数学到通常在本科研究中遇到的高级主题。这一综合性基准涵盖了数论、初等代数、线性代数、抽象代数、微积分、实分析、复分析、泛函分析和概率。这种多样化的数学领域包括的刻意选择使得模型可以在不同抽象级别和推理风格上得到彻底评估。数论和代数问题测试模型处理离散结构和方程的能力，而分析倾向的问题则评估模型对极限、连续性以及微积分的理解。抽象代数和泛函分析部分的题目要求模型对抽象结构和空间进行推理，这需要高级的形式推理能力。评估结果详见表 6。如表所示，具有 CoT 推理的 DeepSeek-Prover-V2-671B 一贯优于所有基线方法，这与之前其他基准评估中的观察趋势一致。

表6：ProverBench 的实验结果。
All 类别代表包含325个问题的完整评估集，而AIME 24&25 表示从最近的AIME竞赛中形式化化得出的15个问题的子集。STP（Dong和Ma，2025）的结果是使用开源模型权重进行评估的。

4. 结论

在本文中，我们提出了一个综合的流程，用于生成冷启动推理数据，以促进形式定理证明的发展。

我们的数据构建过程基于递归定理证明框架，在该框架中，DeepSeek-V3 作为统一模型，用于 Lean 4 证明助手内的子目标分解和引理形式化化。我们的方法结合了高层次的证明草图和形式步骤，形成了一串可管理的子目标序列，这些子目标可以使用更小的 7B 模型高效解决，从而显著减少了计算需求。

我们开发的学习课程框架利用这些分解的子目标生成更难的训练任务，从而创建更有效的学习进度。通过将完整的形式证明与 DeepSeek-V3 的链式推理相结合，我们建立了有价值的冷启动推理数据，将非形式化化的数学思考与形式证明结构联系起来。随后的强化学习阶段显著加强了这一联系，导致形式定理证明能力有了显著提升。

最终生成的模型 DeepSeek-Prover-V2-671B 在一系列基准测试中（涵盖高中竞赛题目和本科数学）一贯优于所有基线方法。

我们未来的工作将侧重于将这一范式扩展到类似于 AlphaProof 的系统，最终目标是解决代表自动定理证明挑战前沿的国际数学 Olympiad（IMO）级别的数学问题。

5. DeepSeek-Prover-V2 模型使用

5.1 模型与数据集下载

我们发布了两种参数规模的 DeepSeek-Prover-V2 模型：7B 和 671B 参数。DeepSeek-Prover-V2-671B 基于 DeepSeek-V3-Base 训练。DeepSeek-Prover-V2-7B 以 DeepSeek-Prover-V1.5-Base 为基础，并具有最大 32K 词元的扩展上下文长度。

模型下载：*

• DeepSeek-Prover-V2-7B：huggingface

• DeepSeek-Prover-V2-671B：huggingface

数据集下载：

DeepSeek-ProverBench：huggingface

5.2 快速入门

你可以直接使用 Huggingface 的 Transformers进行模型推理。DeepSeek-Prover-V2-671B 与 DeepSeek-V3 具有相同的架构。如需详细信息和支持的功能，请参阅 Hugging Face 上的 DeepSeek-V3 文档。

以下是从 miniF2F 数据集生成问题证明的一个基本示例：

from transformers import AutoModelForCausalLM, AutoTokenizer
import torch
torch.manual_seed(30)model_id = "DeepSeek-Prover-V2-7B"  # or DeepSeek-Prover-V2-671B
tokenizer = AutoTokenizer.from_pretrained(model_id)formal_statement = """
import Mathlib
import Aesopset_option maxHeartbeats 0open BigOperators Real Nat Topology Rat/-- What is the positive difference between $120\%$ of 30 and $130\%$ of 20? Show that it is 10.-/
theorem mathd_algebra_10 : abs ((120 : ℝ) / 100 * 30 - 130 / 100 * 20) = 10 := bysorry
""".strip()prompt = """
Complete the following Lean 4 code:\```lean4
{}
\```Before producing the Lean 4 code to formally prove the given theorem, provide a detailed proof plan outlining the main proof steps and strategies.
The plan should highlight key ideas, intermediate lemmas, and proof structures that will guide the construction of the final formal proof.
""".strip()chat = [{"role": "user", "content": prompt.format(formal_statement)},
]model = AutoModelForCausalLM.from_pretrained(model_id, device_map="auto", torch_dtype=torch.bfloat16, trust_remote_code=True)
inputs = tokenizer.apply_chat_template(chat, tokenize=True, add_generation_prompt=True, return_tensors="pt").to(model.device)import time
start = time.time()
outputs = model.generate(inputs, max_new_tokens=8192)
print(tokenizer.batch_decode(outputs))
print(time.time() - start)

参考文献

Azerbayev, Z., Piotrowski, B., Schoelkopf, H., Ayers, E. W., Radev, D., & Avigad, J. (2023). ProofNet: Autoformalizing and formally proving undergraduate-level mathematics. arXiv preprint arXiv:2302.12433.
Barras, B., Boutin, S., Cornes, C., Courant, J., Coscoy, Y., Delahaye, D., de Rauglaudre, D., Filliâtre, J.-C., Giménez, E., Herbelin, H., et al. (1999). The Coq proof assistant reference manual. INRIA, version, 6(11), 17–21.
Barto, A. G., & Mahadevan, S. (2003). Recent advances in hierarchical reinforcement learning. Discrete Event Dynamic Systems, 13, 341–379.
DeepMind. (2024). AI achieves silver-medal standard solving international mathematical olympiad problems. Retrieved from https://deepmind.google/discover/blog/ai-solves-imo-problems-at-silver-medal-level/
DeepSeek-AI. (2024). Deepseek-v3 technical report. Retrieved from https://arxiv.org/abs/2412.19437
DeepSeek-AI. (2025). Deepseek-r1: Incentivizing reasoning capability in llms via reinforcement learning. Retrieved from https://arxiv.org/abs/2501.12948
Dong, K., & Ma, T. (2025). STP: Self-play llm theorem provers with iterative conjecturing and proving. arXiv preprint arXiv:2502.00212.
Dong, K., Mahankali, A., & Ma, T. (2024). Formal theorem proving by rewarding llms to decompose proofs hierarchically. arXiv preprint arXiv:2411.01829.
Eppe, M., Gumbsch, C., Kerzel, M., Nguyen, P. D., Butz, M. V., & Wermter, S. (2022). Intelligent problem-solving as integrated hierarchical reinforcement learning. Nature Machine Intelligence, 4(1), 11–20.
Hendrycks, D., Burns, C., Kadavath, A., Arora, A., Basart, S., Tang, E., Song, D., & Steinhardt, J. (2021). Measuring mathematical problem solving with the MATH dataset. In Thirty-fifth Conference on Neural Information Processing Systems Datasets and Benchmarks Track (Round 2).
Jaech, A., Kalai, A., Lerer, A., Richardson, A., El-Kishky, A., Low, A., Helyar, A., Madry, A., Beutel, A., Carney, A., et al. (2024). Openai o1 system card. arXiv preprint arXiv:2412.16720.
Jiang, A. Q., Welleck, S., Zhou, J. P., Lacroix, T., Liu, J., Li, W., Jamnik, M., Lample, G., & Wu, Y. (2023). Draft, sketch, and prove: Guiding formal theorem provers with informal proofs. In The Eleventh International Conference on Learning Representations.
Lample, G., Lachaux, M.-A., Lavril, T., Martinet, X., Hayat, A., Ebner, A., Rodriguez, A., & Lacroix, T. (2022). Hypertree proof search for neural theorem proving. In Proceedings of the 36th International Conference on Neural Information Processing Systems (pp. 26337–26349).
Li, Y., Du, D., Song, L., Li, C., Wang, W., Yang, T., & Mi, H. (2024). Hunyuanprover: A scalable data synthesis framework and guided tree search for automated theorem proving. arXiv preprint arXiv:2412.20735.
Lin, Y., Tang, S., Lyu, B., Wu, J., Lin, H., Yang, K., Li, J., Xia, M., Chen, D., Arora, S., et al. (2025). Goedel-Prover: A frontier model for open-source automated theorem proving. arXiv preprint arXiv:2502.07640.
Liu, J., Lin, X., Bayer, J., Dillies, Y., Jiang, W., Liang, X., Soletskyi, R., Wang, H., Xie, Y., Xiong, B., et al. (2025). CombiBench: Benchmarking llm capability for combinatorial mathematics. Retrieved from https://moonshotai.github.io/CombiBench/
Moura, L. d., & Ullrich, S. (2021). The Lean 4 theorem prover and programming language. In Automated Deduction–CADE 28: 28th International Conference on Automated Deduction, Virtual Event, July 12–15, 2021, Proceedings 28 (pp. 625–635). Springer.
Nachum, O., Gu, S. S., Lee, H., & Levine, S. (2018). Data-efficient hierarchical reinforcement learning. Advances in Neural Information Processing Systems, 31.
Paulson, L. C. (1994). Isabelle a Generic Theorem Prover. Springer Verlag.
Polu, S., & Sutskever, I. (2020). Generative language modeling for automated theorem proving. arXiv preprint arXiv:2009.03393.
Schulman, J., Wolski, F., Dhariwal, P., Radford, A., & Klimov, O. (2017). Proximal policy optimization algorithms. arXiv preprint arXiv:1707.06347.
Shao, Z., Wang, P., Zhu, Q., Xu, R., Song, J., Zhang, M., Li, Y., Wu, Y., & Guo, D. (2024). DeepSeekMath: Pushing the limits of mathematical reasoning in open language models. arXiv preprint arXiv:2402.03300.
Tsoukalas, G., Lee, J., Jennings, J., Xin, J., Ding, M., Jennings, M., Thakur, A., & Chaudhuri, S. (2024). PutnamBench: Evaluating neural theorem-provers on the putnam mathematical competition. In The Thirty-eight Conference on Neural Information Processing Systems Datasets and Benchmarks Track.
Wang, H., Xin, H., Liu, Z., Li, W., Huang, Y., Lu, J., Zhicheng, Y., Tang, J., Yin, J., Li, Z., et al. (2024a). Proving theorems recursively. In The Thirty-eighth Annual Conference on Neural Information Processing Systems.
Wang, H., Xin, H., Zheng, C., Liu, Z., Cao, Q., Huang, Y., Xiong, J., Shi, H., Xie, E., Yin, J., et al. (2024b). Lego-prover: Neural theorem proving with growing libraries. In The Twelfth International Conference on Learning Representations.
Wang, H., Unsal, M., Lin, X., Baksys, M., Liu, J., Santos, M. D., Sung, F., Vinyes, M., Ying, Z., Zhu, Z., et al. (2025). Kimina-Prover Preview: Towards large formal reasoning models with reinforcement learning. arXiv preprint arXiv:2504.11354.
Wu, Z., Huang, S., Zhou, Z., Ying, H., Wang, J., Lin, D., & Chen, K. (2024). Internlm2.5-stepprover: Advancing automated theorem proving via expert iteration on large-scale lean problems. arXiv preprint arXiv:2410.15700.
Xin, H., Guo, D., Shao, Z., Ren, Z., Zhu, Q., Liu, B., Ruan, C., Li, W., & Liang, X. (2024a). DeepSeek-Prover: Advancing theorem proving in llms through large-scale synthetic data. arXiv preprint arXiv:2405.14333.
Xin, H., Ren, Z., Song, J., Shao, Z., Zhao, W., Wang, H., Liu, B., Zhang, L., Lu, X., Du, Q., et al. (2024b). DeepSeek-Prover-V1.5: Harnessing proof assistant feedback for reinforcement learning and monte-carlo tree search. arXiv preprint arXiv:2408.08152.
Xin, R., Xi, C., Yang, J., Chen, F., Wu, H., Xiao, X., Sun, Y., Zheng, S., & Shen, K. (2025). BFS-Prover: Scalable best-first tree search for llm-based automatic theorem proving. arXiv preprint arXiv:2502.03438.
Yang, K., Poesia, G., He, J., Li, W., Lauter, K., Chaudhuri, S., & Song, D. (2024). Formal mathematical reasoning: A new frontier in AI. arXiv preprint arXiv:2412.16075.
Ying, H., Wu, Z., Geng, Y., Wang, J., Lin, D., & Chen, K. (2024). Lean workbook: A large-scale lean problem set formalized from natural language math problems. In The Thirty-eight Conference on Neural Information Processing Systems Datasets and Benchmarks Track.
Zhang, J., Wang, Q., Ji, X., Liu, Y., Yue, Y., Zhang, F., Zhang, D., Zhou, G., & Gai, K. (2025). Leanabell-prover: Posttraining scaling in formal reasoning. arXiv preprint arXiv:2504.06122.
Zhao, X., Li, W., & Kong, L. (2023). Decomposing the enigma: Subgoal-based demonstration learning for formal theorem proving. arXiv preprint arXiv:2305.16366.
Zhao, X., Zheng, L., Bo, H., Hu, C., Thakker, U., & Kong, L. (2024). Subgoalxl: Subgoal-based expert learning for theorem proving. arXiv preprint arXiv:2408.11172.
Zheng, C., Wang, H., Xie, E., Liu, Z., Sun, J., Xin, H., Shen, J., Li, Z., & Li, Y. (2024). Lyra: Orchestrating dual correction in automated theorem proving. Transactions on Machine Learning Research.
Zheng, K., Han, J. M., & Polu, S. (2022). miniF2F: a cross-system benchmark for formal olympiad-level mathematics. In International Conference on Learning Representations.

版权声明：
本文由 youcans@xidian 对论文 DeepSeek-Prover-V2: Advancing Formal Mathematical Reasoning via Reinforcement Learning for Subgoal Decomposition 进行摘编和翻译，只供研究学习使用。

youcans@xidian 作品，转载必须标注原文链接：
【DeepSeek论文精读】12. DeepSeek-Prover-V2: 通过强化学习实现子目标分解的形式化化数学推理
Copyright 2025 youcans, XIDIAN
Created：2025-05