在扩散模型中，逆向过程的目标是从噪声数据逐步恢复出原始数据。本文将详细解析逆向条件分布 $q({\mathbf{z}}_{t-1}\mid {\mathbf{z}}_t,\mathbf{x})$的推导过程，揭示扩散模型如何通过高斯分布实现数据重建。

---

1. 核心问题

在扩散模型中，我们希望学习如何从含噪数据 $({\mathbf{z}}_t$) 逐步恢复原始数据 $\mathbf{x}$。直接求逆向分布 $q({\mathbf{z}}_{t-1}\mid {\mathbf{z}}_t)$ 是困难的，但若额外已知原始数据 $\mathbf{x}$，则条件分布 $q({\mathbf{z}}_{t-1}\mid {\mathbf{z}}_t,\mathbf{x})$可以简化为高斯分布。

---

2. 贝叶斯定理的应用

利用贝叶斯定理，将条件分布分解为：
$$q({\mathbf{z}}_{t-1}\mid {\mathbf{z}}_t,\mathbf{x})=\frac{q({\mathbf{z}}_t\mid {\mathbf{z}}_{t-1},\mathbf{x})q({\mathbf{z}}_{t-1}\mid \mathbf{x})}{q({\mathbf{z}}_t\mid \mathbf{x})}$$

关键简化：

• 马尔可夫性质：前向过程中，${\mathbf{z}}_t$仅依赖${\mathbf{z}}_{t-1}$，因此：
  $$q({\mathbf{z}}_t\mid {\mathbf{z}}_{t-1},\mathbf{x})=q({\mathbf{z}}_t\mid {\mathbf{z}}_{t-1})$$
  此项由前向过程的定义给出（公式 20.4）：
  $$q({\mathbf{z}}_t\mid {\mathbf{z}}_{t-1})=\mathcal{N}\left({\mathbf{z}}_t;\sqrt{1-{\beta }_t}{\mathbf{z}}_{t-1},{\beta }_t\mathbf{I}\right)$$

• 扩散核：$q({\mathbf{z}}_{t-1}\mid \mathbf{x})$是前向过程的闭式解（公式 20.6）：
  $$q({\mathbf{z}}_{t-1}\mid \mathbf{x})=\mathcal{N}\left({\mathbf{z}}_{t-1};\sqrt{{\alpha }_{t-1}}\mathbf{x},(1-{\alpha }_{t-1})\mathbf{I}\right)$$
  其中${\alpha }_{t-1}={\prod }_{s=1}^{t-1}(1-{\beta }_s)$。

• 分母的忽略：分母 $q({\mathbf{z}}_t\mid \mathbf{x})$ 与${\mathbf{z}}_{t-1}$无关，可视为常数。

---

3. 高斯分布的推导

分子部分是两个高斯分布的乘积：
$$q({\mathbf{z}}_t\mid {\mathbf{z}}_{t-1})\cdot q({\mathbf{z}}_{t-1}\mid \mathbf{x})$$
通过配方法（completing the square），可以合并指数项，得到一个新的高斯分布：
$$q({\mathbf{z}}_{t-1}\mid {\mathbf{z}}_t,\mathbf{x})=\mathcal{N}\left({\mathbf{z}}_{t-1};{\mathbf{m}}_t(\mathbf{x},{\mathbf{z}}_t),{\sigma }_t^2\mathbf{I}\right)$$

均值和方差的计算：

• 均值 (\mathbf{m}_t)：
  $${\mathbf{m}}_t(\mathbf{x},{\mathbf{z}}_t)=\frac{\sqrt{{\alpha }_{t-1}}{\beta }_t}{1-{\alpha }_t}\mathbf{x}+\frac{\sqrt{1-{\beta }_t}(1-{\alpha }_{t-1})}{1-{\alpha }_t}{\mathbf{z}}_t$$
  这是原始数据$\mathbf{x}$和当前噪声数据${\mathbf{z}}_t$的线性组合。

• 方差 ${\sigma }_t^2$：
  $${\sigma }_t^2=\frac{(1-{\alpha }_{t-1}){\beta }_t}{1-{\alpha }_t}$$
  仅依赖噪声调度参数${\beta }_t$和累积系数${\alpha }_t$。

---

4. 直观理解

• 给定$\mathbf{x}$的重要性：若已知原始数据$\mathbf{x}$，则从 ${\mathbf{z}}_t$推断 ${\mathbf{z}}_{t-1}$是一个确定性更强的去噪问题，解为高斯分布。
• 物理意义：均值 ${\mathbf{m}}_t$是“部分去噪”的结果，方差 ${\sigma }_t^2$表示剩余的不确定性。

---

5. 与逆向过程的关系

实际训练中，我们无法直接使用 $\mathbf{x}$（因需生成新数据），因此：

1. 用神经网络 $p_{\theta }({\mathbf{z}}_{t-1}\mid {\mathbf{z}}_t)$近似$q({\mathbf{z}}_{t-1}\mid {\mathbf{z}}_t,\mathbf{x})$。
2. 网络通过预测均值 ${\mathbf{m}}_t$ 或噪声 $\mathbf{ϵ}$来学习去噪。

---

6. 总结

• 数学本质：通过贝叶斯定理和高斯分布的性质，显式推导出条件逆向分布的闭式解。
• 实际意义：指导神经网络学习去噪步骤的理论基础。
• 关键公式：
  $$q({\mathbf{z}}_{t-1}\mid {\mathbf{z}}_t,\mathbf{x})=\mathcal{N}\left({\mathbf{z}}_{t-1};{\mathbf{m}}_t(\mathbf{x},{\mathbf{z}}_t),{\sigma }_t^2\mathbf{I}\right)$$

这种推导是扩散模型理论的核心，确保了从噪声中生成数据的数学严谨性。

---

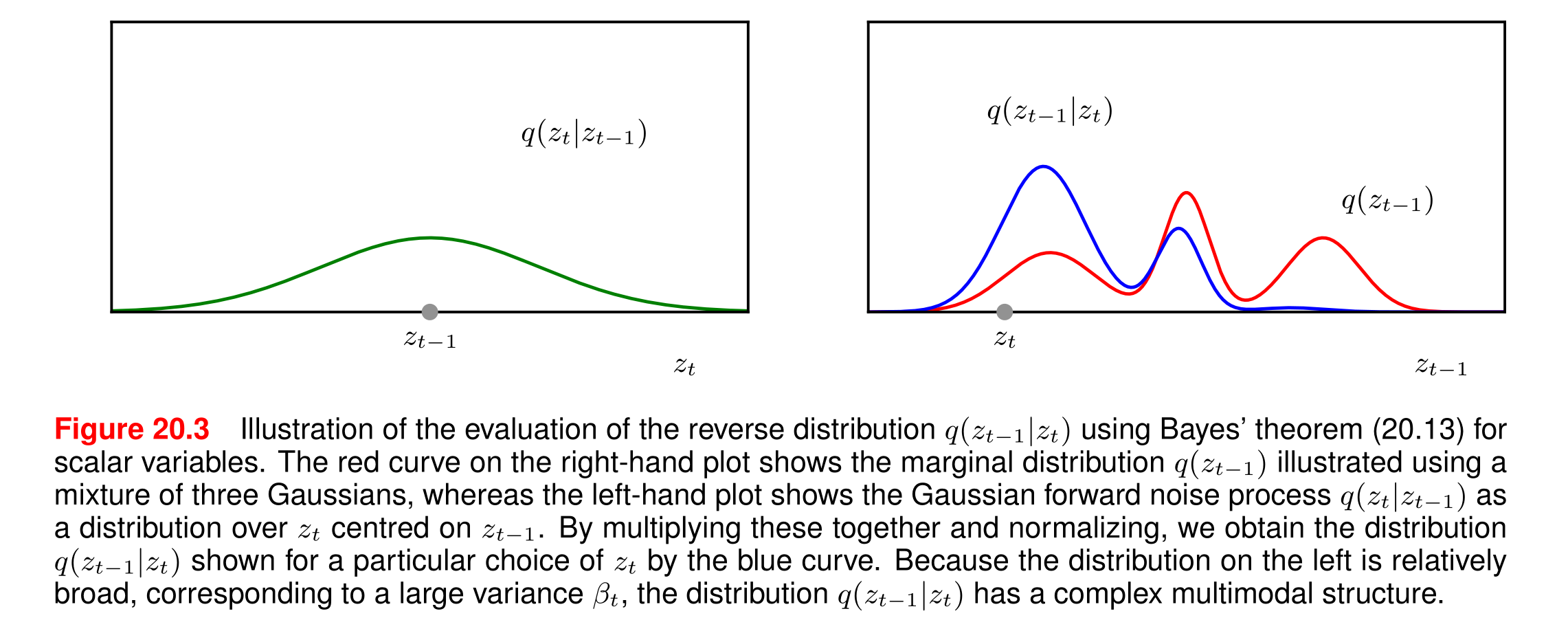
这张图（图20.3）展示了扩散模型中逆向分布的计算过程，以下是详细解析：

---

1. 图的组成与含义

(1) 左子图：前向噪声过程$q(z_t|z_{t-1})$

• 横轴：噪声数据 $z_t$
• 纵轴：概率密度
• 曲线特征：以 $z_{t-1}$为中心的高斯分布（钟形曲线）
• 关键参数：方差${\beta }_t$较大 → 曲线"宽泛"（平坦）
• 物理意义：表示单步加噪时，$z_t$ 可能取值的范围较大

(2) 右子图：边缘分布$q(z_{t-1})$

• 横轴：数据 $z_{t-1}$
• 纵轴：概率密度
• 红色曲线：三个高斯分布的混合（多峰结构）
• 物理意义：反映数据在$t-1$ 步的整体分布（可能对应不同模态的真实数据）

(3) 蓝色曲线：逆向分布$q(z_{t-1}|z_t)$

• 生成方式：通过贝叶斯定理将左、右子图的分布相乘并归一化
• 特征：复杂多峰结构（多个局部最大值）
• 物理意义：给定当前噪声$z_t$，可能对应多个潜在的 $z_{t-1}$状态

---

2. 关键句解析

“由于左侧分布（对应大方差βt）相对宽泛，导致逆向分布$q(zt-1|zt)$呈现出复杂的多峰结构。”

(1) 因果关系

• 大方差 ${\beta }_t$ → 前向分布 $q(z_t|z_{t-1})$ 平坦 → 允许 $z_t$ 偏离 $z_{t-1}$更远
• 结果：一个 $z_t$可能由多个不同的$z_{t-1}$生成 → 逆向分布出现多峰

(2) 多峰结构的含义

• 每个峰：对应一个可能的$z_{t-1}$ 来源
• 示例：若原始数据包含"猫"和"狗"两类，加噪后的$z_t$可能无法确定源自哪类 → 逆向分布同时保留两种可能

(3) 数学解释

贝叶斯定理中：
$$q(z_{t-1}|z_t)\propto \underset{\text{宽泛分布}}{\underbrace{q(z_t|z_{t-1})}}\cdot \underset{\text{多峰分布}}{\underbrace{q(z_{t-1})}}$$

• 宽泛的似然$q(z_t|z_{t-1})$不会压制$q(z_{t-1})$ 的多峰性
• 最终逆向分布继承$q(z_{t-1})$ 的多峰特征

---

3. 对扩散模型的意义

1. 理论挑战：多峰性说明直接计算逆向分布极其困难
2. 解决方案：
   • 用神经网络$p_{\theta }(z_{t-1}|z_t)$近似为单峰高斯
   • 通过训练使网络学会选择"最可能"的峰（对应高质量生成）
3. 设计启示：
   • 需控制${\beta }_t$大小：方差过大导致多峰性增强，训练难度增加
   • 多峰性也赋予模型捕捉数据多样性的能力

---

4. 实例说明

假设：

• 右子图的三个峰对应$z_{t-1}=-1,0,1$（三种潜在状态）
• 观测到$z_t=0.5$（左子图中心在某个 $z_{t-1}$
• 蓝色曲线可能在$z_{t-1}=0$和$z_{t-1}=1$处各有一个峰
  → 说明$z_t=0.5$可能由$z_{t-1}=0$或$1$ 加噪得到

---

5. 总结

该图揭示了扩散模型中逆向过程的本质困难：
前向噪声的随机性（大方差）导致逆向推断存在歧义，而模型必须通过学习解决这种歧义，才能实现高质量生成。这一现象也解释了为什么扩散模型需要复杂的网络结构和训练技巧。

---

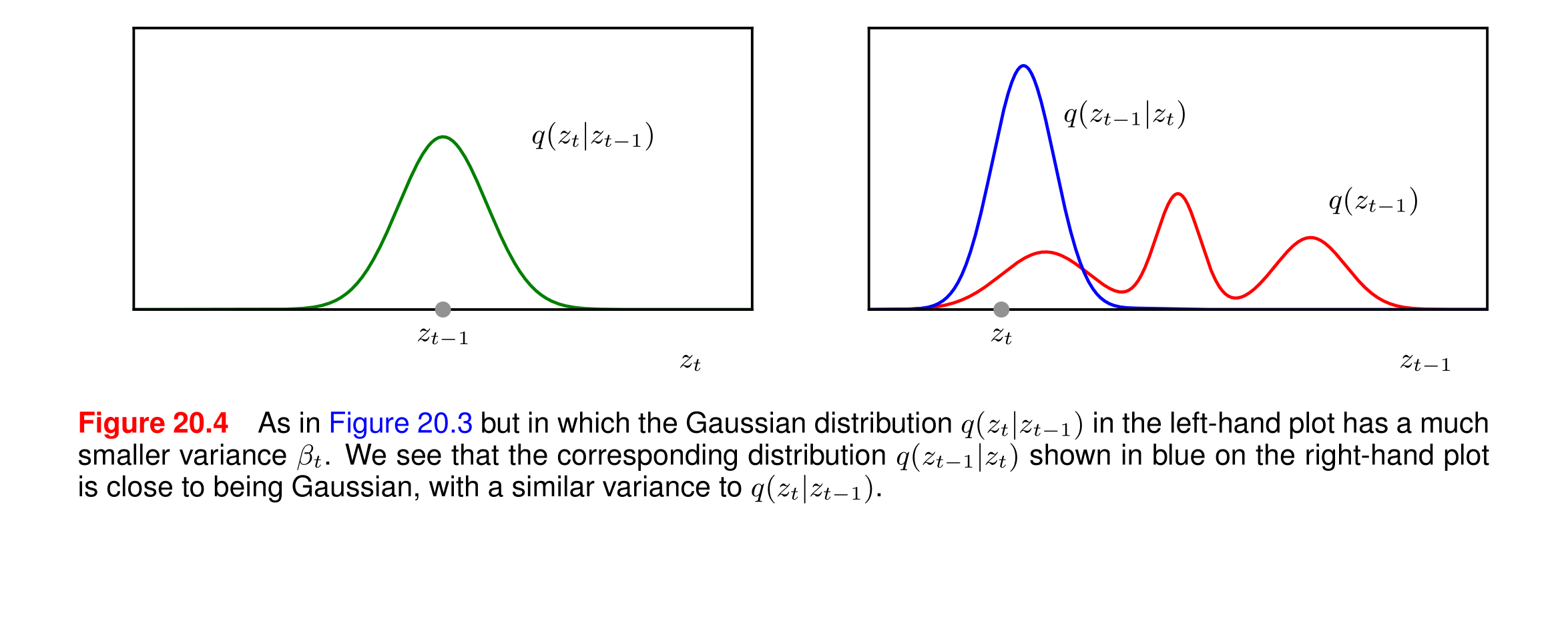
在图20.4中，左图展示了条件概率分布$q(z_t|z_{t-1})$，其方差${\beta }_t$较小，这意味着分布更窄。右图展示了相应的逆过程分布$q(z_{t-1}|z_t)$。

为什么分布更窄并不意味着变化更明显？

1. 方差与变化幅度：

   • 方差是衡量数据分布的离散程度的指标。较小的方差意味着数据点更集中在均值附近。
   • 在条件概率分布 $q(z_t|z_{t-1})$中，较小的方差表示在给定 $z_{t-1}$ 的情况下， $z_t$ 的取值更集中在某个特定值附近，即 $z_t$ 的变化幅度较小。

2. 逆过程分布：

   • 右图中的蓝色曲线 $q(z_{t-1}|z_t)$展示了在给定 $z_t$的情况下， $z_{t-1}$ 的分布。
   • 由于左图中的 $q(z_t|z_{t-1})$ 分布较窄，意味着 $z_t$ 的取值相对集中，因此在逆过程中， $z_{t-1}$ 的分布也相对集中，接近高斯分布。

3. 变化幅度与学习难度：

   • 分布更窄意味着在每一步变换中，潜在变量的变化幅度较小。这种微小的变化使得模型更容易学习如何逆转这些变换，因为每一步的变换都是可预测的、稳定的。
   • 如果方差较大，潜在变量的变化幅度会更大，这会增加模型学习逆过程的难度，因为每一步的变换更加不可预测。

总结

• 分布更窄（方差较小）意味着潜在变量的变化幅度较小，而不是变化更明显。
• 这种微小的变化使得逆过程更容易学习和预测，因为每一步的变换都是相对稳定和可预测的。
• 因此，较小的方差有助于简化模型的学习过程，但可能需要更多的步骤来达到显著的总体变化。