爱因斯坦关系式 $D=u{k}_{B}T$ 将扩散系数($D$)与迁移率($u$)通过玻尔兹曼常数($k_B$)和温度($T$)联系起来，是连接微观热运动与宏观输运现象的重要桥梁。

从涨落理论和能量均分定理的数学推导

基于平衡统计力学的推导

最直接的推导始于热平衡条件下的粒子流平衡。

在外势场U(x)作用下，系统中存在两种相互竞争的粒子流：

漂移流: $J_{drift}=-\mu \rho \nabla U$，其中μ为迁移率，ρ为粒子密度
扩散流: $J_{diffusion}=-D\nabla \rho$，遵循菲克定律

热平衡要求总流为零：$J_{drift}+J_{diffusion}=0$

对于经典粒子系统，密度遵循麦克斯韦-玻尔兹曼分布：$\rho (x)={\rho }_{0}exp(-U(x)/k_{B}T)$

因此：$d\rho /dU=-\rho /k_{B}T$

将此关系代入平衡条件得到：$0=-\mu \rho \nabla U-D\nabla \rho =-\mu \rho \nabla U-D(-\rho /k_{B}T)\nabla U$

消去公共项，立即得到爱因斯坦关系式：$D=\mu k_{B}T$

我来详细解释这个推导中每一步的物理原因：

1. 漂移流的来源：$J_{drift}=-\mu \rho \nabla U$

物理机制

当粒子处在外势场 U(x) 中时，会受到力：$F=-\nabla U$

这个力会驱动粒子定向运动。在存在阻力的介质中（如液体），粒子很快达到终端速度：$v_{drift}=\mu F=-\mu \nabla U$

其中 μ 是迁移率，定义为单位力作用下的漂移速度。

粒子流的形成

如果位置 x 处的粒子密度为 ρ(x)，则该处的粒子流（单位时间通过单位面积的粒子数）为：$J_{drift}=\rho (x)\cdot v_{drift}=-\mu \rho \nabla U$

负号的意义：粒子沿着势能降低的方向运动（从高势能向低势能）。

2. 扩散流的来源：$J_{diffusion}=-D\nabla \rho$

菲克第一定律描述了稳态扩散过程中扩散通量与浓度梯度的关系。以下是详细推导：

1. 稳态扩散：浓度分布不随时间变化，$\partial C/\partial t=0$
2. 分子热运动：分子因热运动而随机移动
3. 浓度驱动：扩散由浓度差驱动，总是从高浓度向低浓度进行

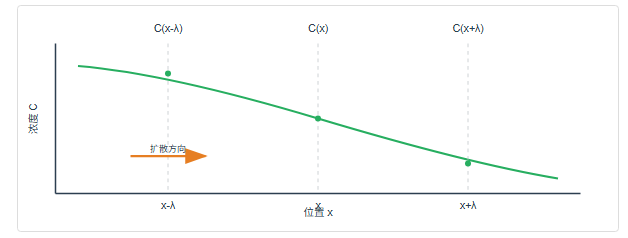
设想一个一维系统，在x方向上存在浓度梯度。取厚度为dx的薄层进行分析。

• 分子平均热运动速度：v̄
• 分子平均自由程：λ
• 在x位置处的浓度：C(x)

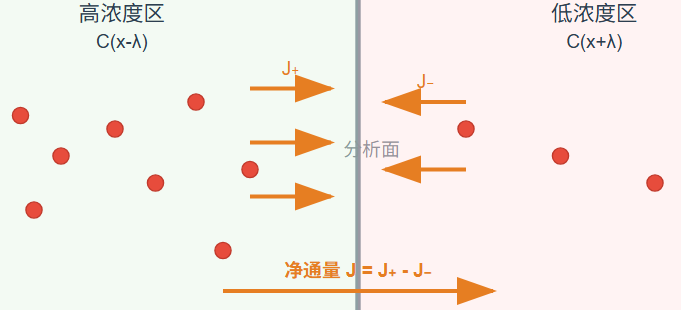
从左侧进入的分子通量：

• 距离为λ处的浓度：$C(x-\lambda )$
• 向右运动的分子数密度：$C(x-\lambda )/6$ (考虑三维随机运动，每个方向占1/6)
• 通量：$J_{+}=(\bar{v}/6)\times C(x-\lambda )$

从右侧进入的分子通量：

• 距离为λ处的浓度：$C(x+\lambda )$
• 向左运动的分子数密度：$C(x+\lambda )/6$
• 通量：$J_{-}=(\bar{v}/6)\times C(x+\lambda )$

净扩散通量（向右为正）：$J=J_{+}-J_{-}=(\bar{v}/6)[C(x-\lambda )-C(x+\lambda )]$

对于小的λ，进行泰勒展开：
$$\begin{gathered} C(x-\lambda )\approx C(x)-\lambda (\partial C/\partial x) \\ C(x+\lambda )\approx C(x)+\lambda (\partial C/\partial x) \end{gathered}$$

代入得：
$$\begin{gathered} J=(\bar{v}/6)[(C(x)-\lambda \partial C/\partial x)-(C(x)+\lambda \partial C/\partial x)] \\ J=(\bar{v}/6)(-2\lambda \partial C/\partial x) \\ J=-(\bar{v}\lambda /3)(\partial C/\partial x) \end{gathered}$$

根据动力学理论：$D=\bar{v}\lambda /3$，其中D为扩散系数，具有量纲$[L^2{T}^{-1}]$。

最终得到：$J=-D(\partial C/\partial x)$

• 负号：表示扩散方向与浓度梯度方向相反，即从高浓度向低浓度扩散
• D：扩散系数，反映物质的扩散能力，与温度、分子大小、介质性质有关
• ∂C/∂x：浓度梯度，是扩散的驱动力

对于三维情况：$J=-D\nabla C$

3. 热平衡要求总流为零

热平衡的定义

热平衡意味着：

• 系统各处温度相同
• 没有宏观的粒子流动
• 粒子密度分布不随时间变化

流平衡的必要性

如果 $J_{total}=J_{drift}+J_{diffusion}\ne 0$，则：

• 某些区域粒子会积累
• 另一些区域粒子会耗尽
• 密度分布会随时间变化

这违反了热平衡的定义，因此必须有：
$$J_{drift}+J_{diffusion}=0$$

4. 密度遵循麦克斯韦-玻尔兹曼分布？

统计力学的基本原理

在热平衡下，粒子在相空间中的分布由玻尔兹曼因子决定：
$$P(位置在x处)\propto exp(-U(x)/k_{B}T)$$

这来自于：

1. 最大熵原理：在给定能量约束下，系统趋向于熵最大的状态
2. 正则系综：与热库接触的系统，各微观态的概率正比于 $exp(-E/k_{B}T)$

密度分布的推导

粒子密度正比于在该位置找到粒子的概率：
$$\rho (x)={\rho }_0\cdot exp(-U(x)/k_{B}T)$$

其中 ${\rho }_0$ 是归一化常数（通常是 U=0 处的密度）。

这个系统展现了两种基本物理过程的竞争：

1. 势能驱动的有序化：外势场试图将粒子聚集在低势能区域
2. 熵驱动的无序化：热运动试图使粒子均匀分布

朗之万方程推导

更深层的推导来自朗之万方程，它直接从牛顿第二定律出发描述布朗粒子的运动：

$m(d^{2}x/d{t}^2)=-\gamma (dx/dt)+R(t)$

其中γ为摩擦系数，R(t)为随机力，满足：

• $⟨R(t)⟩=0$
• $⟨R(t)R(t^{\prime })⟩=2\gamma k_{B}T\delta (t-t^{\prime })$ （涨落-耗散关系）

通过将方程两边同时乘以x并取系综平均，运用能量均分定理：$⟨½m(dx/dt{)}^2⟩=½k_{B}T$

经过完整的数学分析，可得到：$⟨x^2(t)⟩=2Dt$，其中 $D=k_{B}T/\gamma$

由于迁移率$\mu =1/\gamma$，最终得到：$D=\mu k_{B}T$

涨落-耗散定理推导

最一般的推导来自涨落-耗散定理，它表明热涨落的关联函数与系统对外扰动的响应函数直接相关：$S_x(\omega )=(2k_{B}T/\omega )Im[\chi (\omega )]$

对于布朗运动，速度关联函数为：$⟨v(0)v(t)⟩=(k_{B}T/m)exp(-\gamma t/m)$

扩散系数通过积分得到：$D={\int }_0^{\infty }⟨v(0)v(t)⟩dt=kBT/\gamma =\mu kBT$

原始文献和重要参考文献

爱因斯坦的开创性工作

原始论文：

• 标题：《分子运动论所要求的静止液体中悬浮粒子的运动》
• 德文原题：“Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen”
• 期刊：Annalen der Physik, Vol. 17, pp. 549-560 (1905)

其他重要贡献者

斯莫卢霍夫斯基 (Marian Smoluchowski, 1906)：

• 论文：“Zur kinetischen Theorie der Brownschen Molekular Bewegung und der Suspensionen”
• 期刊：Annalen der Physik, Vol. 21, pp. 756-780

朗之万 (Paul Langevin, 1908)：

• 论文：“Sur la théorie du mouvement brownien”
• 期刊：Comptes Rendus, Vol. 146, pp. 530-533

物理意义

基本物理图像

爱因斯坦关系揭示了一个深刻的物理洞察：驱动随机扩散的热涨落与决定粒子对外力响应的机制是同一个。这种统一性体现在：

1. 微观机制统一：分子碰撞既造成随机游走(扩散)，也产生系统阻力(影响迁移率)
2. 能量尺度统一：kBT设定了热涨落和响应现象的特征能量尺度
3. 时间尺度关联：扩散时间与响应时间通过同一组输运系数相关

现代应用领域

半导体物理：

• 电子和空穴在半导体中的输运
• 器件建模中的漂移-扩散方程
• 太阳能电池和LED的性能优化

电化学 - 能斯特-爱因斯坦关系：

$\Lambda =(F^2/RT)({\nu }_{+}{z}_{+}^2{D}_{+}+{\nu }_{-}{z}_{-}^2{D}_{-})$

应用于电池电解质优化、燃料电池性能、腐蚀过程分析

物理意义的深层理解

关系式的核心意义在于建立了平衡态统计力学的普遍联系：

• 涨落 (扩散系数D) 与 耗散 (迁移率的倒数) 通过热力学温度相关
• 体现了热力学第二定律的微观基础
• 是更一般的涨落-耗散定理的特殊情况

玻尔兹曼常数$k_B$与理想气体常数R的关系作用

基本关系 $R=k_B{N}_A$

这一关系连接了单个粒子的微观性质与摩尔量的宏观测量：

• $k_B$ = 1.380649 × 10⁻²³ J/K (单个粒子尺度)
• R = 8.314 J/(mol·K) (摩尔尺度)
• $N_A$ = 6.02214076 × 10²³ mol⁻¹ (阿伏伽德罗数)

在推导中的关键作用

微观-宏观桥梁：$k_B$提供了连接统计力学与热力学的基本桥梁

• 统计熵：$S=k_{B}lnW$
• 热力学熵：$S=\int dQ/T$
• 确保两种描述的一致性

能量尺度设定：$k_{B}T$作为特征能量出现在：

• 经典极限：每个自由度的平均动能 = $½k_{B}T$ (能量均分定理)
• 玻尔兹曼分布：概率 ∝ $exp(-E/k_{B}T)$
• 激活过程：速率 ∝ $exp(-Ea/k_{B}T)$

推导中的核心地位：
在平衡态推导中，麦克斯韦-玻尔兹曼分布 $\rho \propto exp(-U/k_{B}T)$ 中的$k_{B}T$直接来自能量均分定理，确保了：

1. 热平衡的统计力学描述
2. 宏观输运系数的正确关联
3. 实验可测量量之间的定量关系

热力学一致性

$R=k_B{N}_A$关系保证了：

• 单分子水平的爱因斯坦关系 $D=\mu k_{B}T$
• 摩尔水平的能斯特-爱因斯坦方程 $D=\mu RT/F$ (对带电粒子)
• 宏观电导率测量与微观迁移率的正确换算

结论与现代意义

爱因斯坦关系式 $D=\mu k_{B}T$ 远非简单的比例关系，它体现了统计力学的核心思想：热平衡态下涨落与耗散的普遍联系。这一关系的推导过程展现了：

1. 数学严谨性：从涨落理论、朗之万方程到涨落-耗散定理的多重推导路径
2. 物理深刻性：揭示了随机热运动与系统响应的内在统一
3. 应用广泛性：从经典布朗运动到现代纳米技术的跨尺度应用
4. 历史重要性：提供了验证原子理论的关键实验途径