一、图的定义
1、什么是图?
图G=(V,E) 如图,无向图G
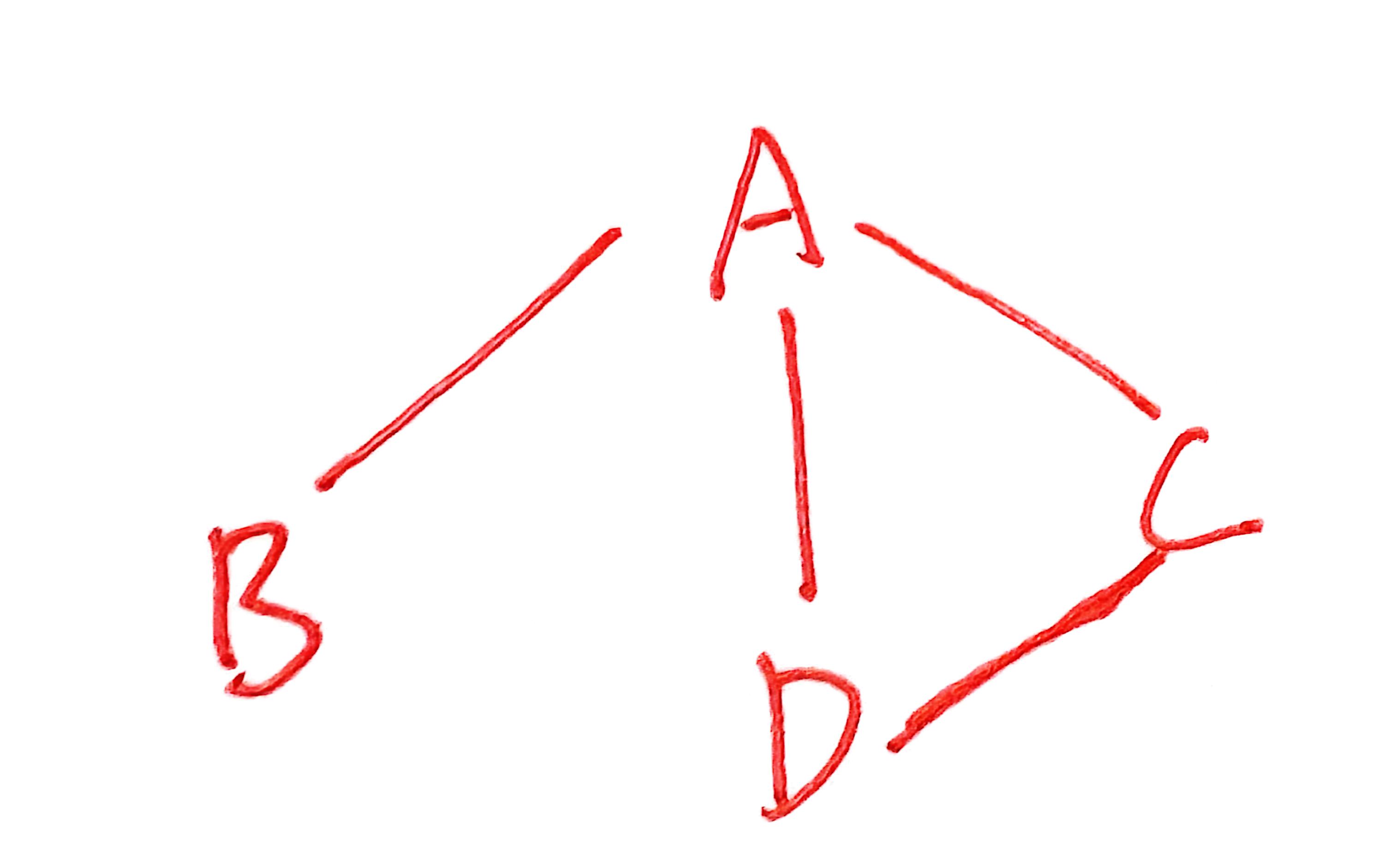
顶点集V={,
,...,
},用|V|表示图G的顶点个数
如:V={A,B,C,D} ,|V|=4
边集E={(u,v)|uV, v
V}, 用|E|表示图G的边的条数
如:E={(u,v)|(A,B),(A,D),(A,C),(C,D)},|E|=4zhu
注:
1、图不可以是空图。线性表可以是空表,树可以是空树
2、图中不能一个顶点都没有,V非空
3、但是图中可以没有边,E为空,此时图中只有顶点没有边
2、简单图和多重图
简单图的条件:
1、不存在重复边
2、不存在顶点到自身的边

多重图的条件:
某两个顶点之间的变数大于1条,又允许顶点通过一条边自身关联
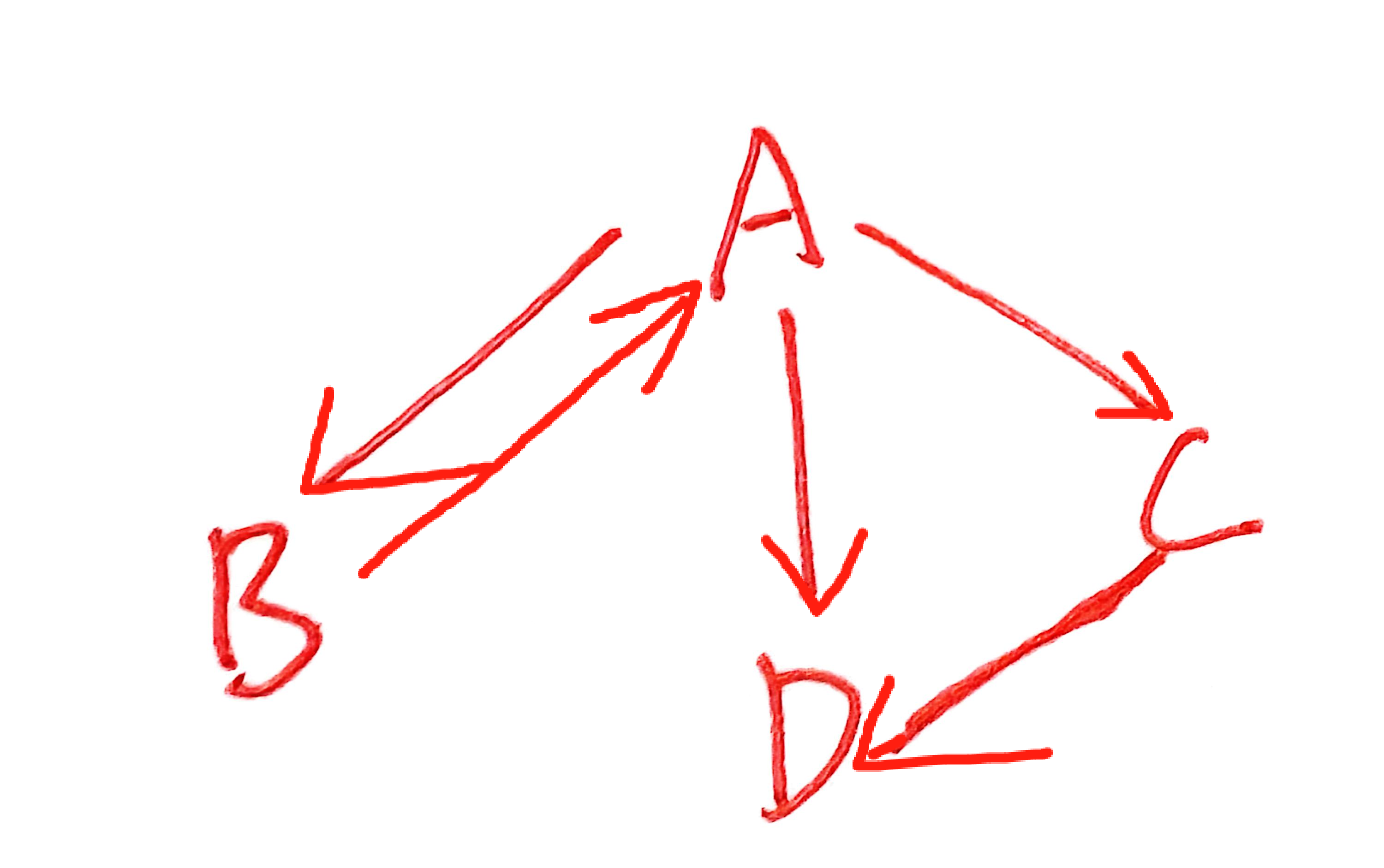
3、有向图
E是有向边(简称弧)的有限集合,弧是顶点的有序对。
记为<v,w>,v为弧头,w为弧尾。也称v邻接到w。
如图为有向图G,注意边集E={(u,v)|(A,B),(B,A),(A,C),(A,D),(C,D)},AB两个顶点有两条边

4、无向图
E是无向边的有限结合,边是顶点的无序对。
记为<v,w>或<w,v>,也称v和w互为邻接点。

5、顶点的度,入度、出度
顶点的度针对无向图、有向图,所有顶点的度=边数*2
入度、出度仅用于有向图
无向图
| 有向图
| |
| 顶点v的度 | 依附于顶点v的边的条数 如图,顶点A的度=3 | 顶点v的度分为入度和出度 如图,顶点A的度=入度+出度=1+3=4 入度是以顶点v为终点的有向边的数目 出度是以顶点v为起点的有向边的数目 |
| 图的度 | 所有顶点的度之和 =边数*2 如图,图的度(全部顶点的度)=8 | 所有顶点的入度之和 = 所有顶点的出度之和 =边数 所有顶点的度之和 =边数*2 如图,图的入度(全部顶点的入度)=5 图的出度(全部顶点的出度)=5 图的度(全部顶点的度)=10 |
6、路径、路径长度、回路
1、路径
顶点A到顶点D的之间的一条路径是指顶点序列A,C,D,关联的边也是路径的构成要素
简单路径——顶点不重复

2、路径上的边的数目成为路径长度
如,顶点A到顶点D的路径长度为2
3、第一个顶点和最后一个顶点相同的路径成为回路或环
简单回路——除第一个顶点和最后一个顶点之外,其他顶点不重复的回路
如,A-C-D-A
注:
1、若一个图有n个顶点,并且大于n-1条边,则此图一定有环
7、距离
顶点间最短路径,则此路径的长度称为距离
若两点之间不存在路径,则距离为无穷(∞)
8、子图
G=(V,E)和=(
,
),若
是V的子集,
是G的子集,则称
是G的子图
V()=V(G),则称其为G的生成子图。 (即包含所有顶点)
注:
并非V和E的任何子集都能构成子图
如果
中某些边的顶点不再
中,此时不是图
9、连通、连通图、连通分量
此节仅针对无向图,有向图与强连通有关
1、连通——顶点v到顶点w有路径存在
2、连通图——任意两个顶点之间均连通
若有n个顶点,至少n-1条边,成为连通图;

若有n个顶点,至多条边,不是连通图;
计算方法:排除一个点,将其余点的边都铺满
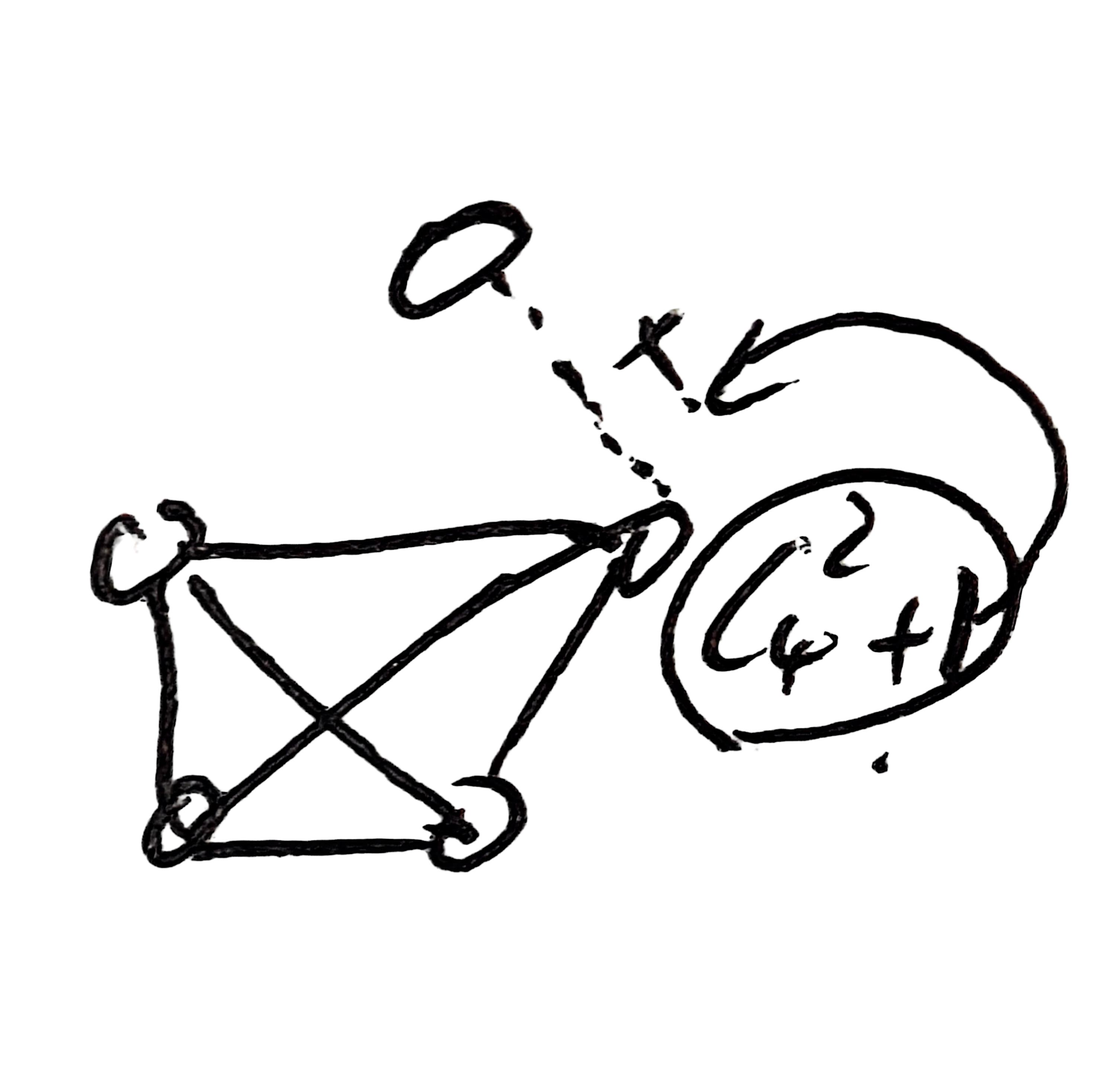 此时,
此时,,一旦达到就会形成连通图。
3、连通分量——无向图中的极大连通子图
极大连通子图——子图必须连通,包含尽可能多的顶点和边
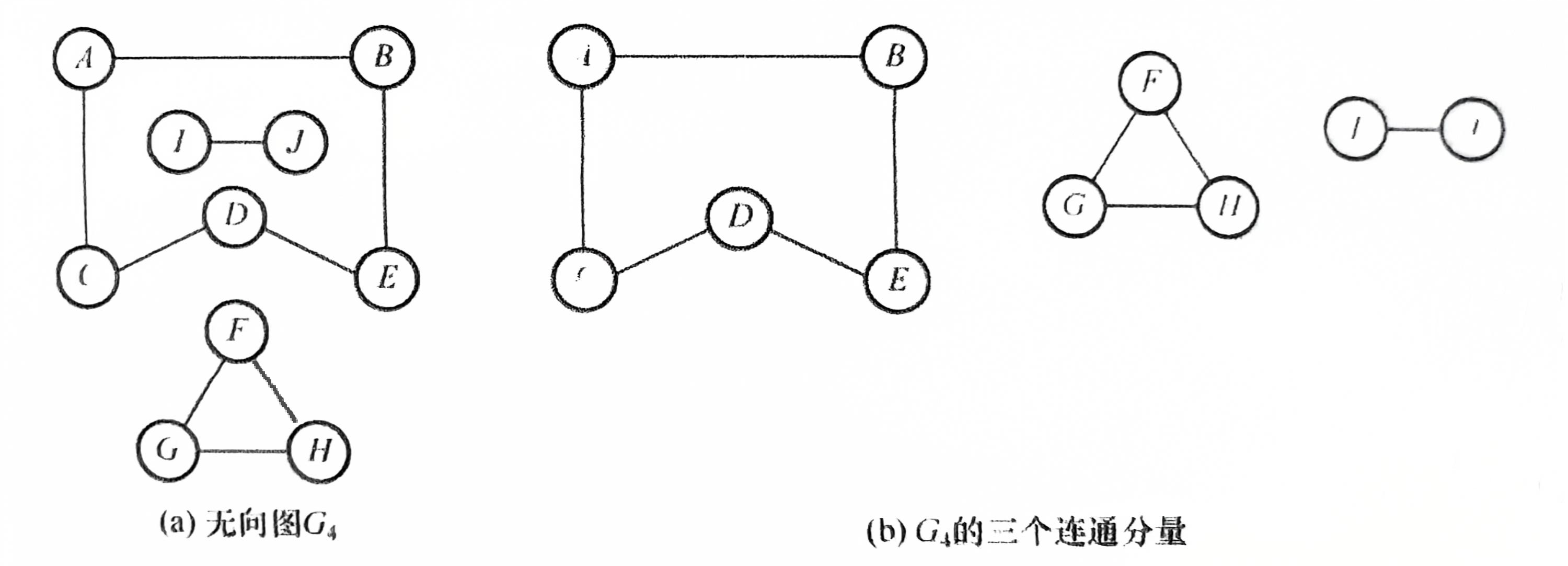
10、强连通图、强连通分量
此节仅针对有向图,无向图与连通有关
1、强连通——从顶点v到顶点w和从顶点w到顶点v都有路径
2、强连通图——任意一对顶点强连通
若有n个顶点,至少n条边,成为强连通图

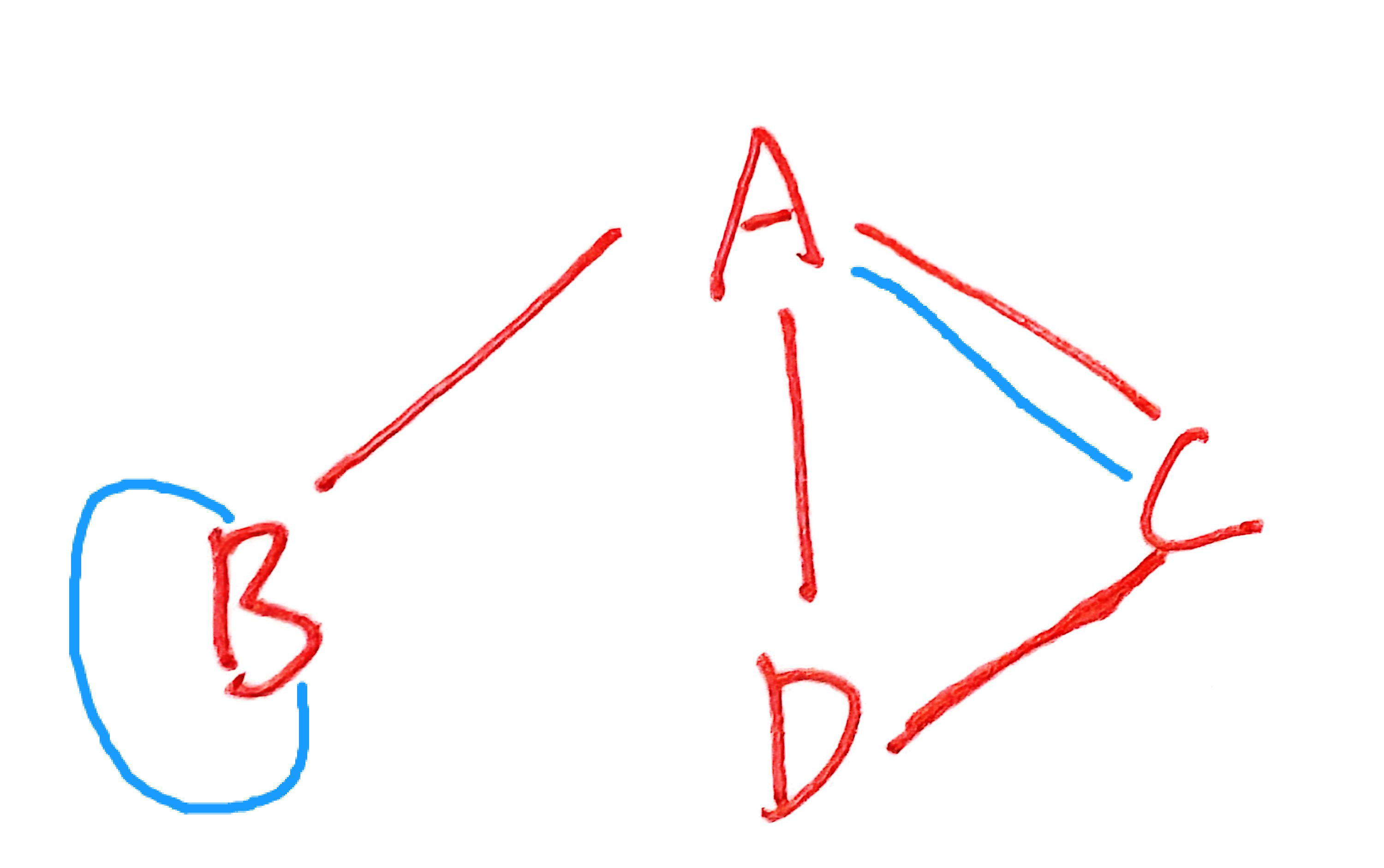
3、强连通分量——有向图中的极大强连通子图
如图,虚线内记为极大强连通子图

11、生成树、生成森林
连通图的生成树——包含图中全部顶点的一个极小连通子图
极小连通子图——包含图中的全部顶点,保持子图连通且边数尽可能少
图中顶点数为n,则生成树含有n-1条
砍一条边->非连通图 加一条边->回路
在非连通图中,连通分量的生成树构成了非连通图的生成森林
12、边的权、网、带权路径长度
边上带有权值的图称为带权图,也称为网。
路径上所有边的权值之和,称为该路径的带权路径长度。
13、完全图(也称简单完全图)
对于无向图,有条边的无向图称为无向完全图,即完全图中任意两个顶点之间都存在边
对于有向图,有n(n-1)条弧的有向图称为有向完全图,即任意两个顶点之间都存在方向相反的两条弧。也就是条边。
14、有向树
有向树——一个顶点的入度为0,其余顶点的入度均为1的有向图
有向树不是强连通图
n个顶点的树,必有n-1条边
n个顶点的图,若|E|>n-1,则一定有回路
二、易混淆定义
若一个图有n个顶点,并且大于n-1条边,则此图一定有环
图中顶点数为n,则生成树含有n-1条
若有n个顶点,至少n-1条边,成为连通图;
若有n个顶点,至多
条边,不是连通图;
若有n个顶点,至少n条边,成为强连通图
距离、路径长度、带权路径长度








安全运维工程师)
)



)


)

)
