网址：主站

工具补充

1. sort 函数的使用规则

• 作用：对容器元素进行排序，默认升序。
• 语法：sort(起始迭代器, 结束迭代器, 比较规则)
  • 前两个参数是排序范围：[begin, end)（包含begin，不包含end）。
  • 第三个参数可选：自定义比较规则（默认用 < 比较，即升序）。
• 代码场景：
  sort(jobs.begin(), jobs.end(), [](const vector<int>& a, const vector<int>& b) { return a[1] < b[1]; })
  表示按 jobs 中每个子数组的第二个元素（结束时间）升序排序。
  • 为什么用 <？因为比较规则返回 true 时，a 会排在 b 前面。a[1] < b[1] 意味着“结束时间小的 job 排在前面”，即升序。

2. begin() 和 end() 迭代器

• 迭代器：可理解为“容器元素的指针”，用于访问容器元素。
• begin()：返回指向容器第一个元素的迭代器。
• end()：返回指向容器最后一个元素之后的迭代器（标记范围终点，不指向实际元素）。
• 用途：搭配算法（如 sort）指定操作范围，形成 [begin, end) 左闭右开区间，确保遍历/排序不越界。

3. Lambda 表达式（匿名函数）

• 格式：[捕获列表](参数列表) { 函数体 }
  此处 [] 表示无捕获，(const vector<int>& a, const vector<int>& b) 是参数，{ return a[1] < b[1]; } 是函数体。
• 作用：临时定义短小的函数，作为 sort 等算法的自定义比较规则。
• 代码场景：告诉 sort 如何比较两个 job——用它们的结束时间（a[1] 和 b[1]）比较，实现按结束时间排序。

4. rbegin() 反向迭代器

• 作用：返回容器的反向起始迭代器，指向容器最后一个元素（与 begin() 方向相反）。
• 代码场景：dp.rbegin() 指向 map 中键最大的元素（因为 map 按键升序排列，最后一个元素键最大）。
  dp.rbegin()->second 即获取当前最大时间对应的最大利润（不选择当前工作时的最大利润）。

5. ->second 访问 map 的值

• map 存储的是键值对（pair<key, value>），迭代器指向 pair 对象。
• ->first：访问键（key）；->second：访问值（value）。
• 代码场景：dp 中键是时间，值是该时间的最大利润。prev(...)->second 即获取“开始时间前的最大利润”。

6. prev() 函数

• 作用：返回迭代器的前一个位置（即 --iterator 的结果），需迭代器支持 -- 操作（如 map 的迭代器）。
• 代码场景：prev(dp.upper_bound(begin)) 用于获取“最后一个键 <= begin 的元素迭代器”（配合 upper_bound 查找）。

7. 二分相关库函数汇总

核心逻辑关联

代码通过 sort 按结束时间排序 jobs，用 map 存储“时间-最大利润”映射，借助 upper_bound+prev 快速找到不冲突的历史最大利润，用 rbegin 获取当前最大利润，最终通过动态规划选择最优解。这些工具共同实现了高效的时间复杂度（O(nlogn)）。

排序算法

排序关键指标：

1. 时空复杂度；
2. 排序稳定性：
   • 排序后相对位置没有发生改变，单单排int类型意义不大，但是对于复杂的数据，比如订单数据，有订购时间和用户id，那如果是稳定排序，排序后相同用户id依然会按照交易日期有序排列；
   • 如果用不稳定排序，相同用户id的订单相对位置可能变化，
3. 是否原地排序：是否不需要额外的辅助空间，只需要常数级别额外空间？能否最直接操作原数组？

1. 选择排序【不稳定】

• 遍历一遍数组，找到最小值
• 与数组第一个元素交换
• 接着从第二个开始重复以上操作

void sort(vector<int>& nums) {int n = nums.size();// sortedIndex 是一个分割线// 索引 < sortedIndex 的元素都是已排序的// 索引 >= sortedIndex 的元素都是未排序的// 初始化为 0，表示整个数组都是未排序的int sortedIndex = 0;while (sortedIndex < n) {// 找到未排序部分 [sortedIndex, n) 中的最小值int minIndex = sortedIndex;for (int i = sortedIndex + 1; i < n; i++) {if (nums[i] < nums[minIndex]) {minIndex = i;}}// 交换最小值和 sortedIndex 处的元素int tmp = nums[sortedIndex];nums[sortedIndex] = nums[minIndex];nums[minIndex] = tmp;// sortedIndex 后移一位sortedIndex++;}
}

• 空间复杂度是 O(1)，是个原地排序。
• 时间复杂度 $O(n^2)$，嵌套for循环
• 数组本来有序性对算法执行次数的影响：无影响，即便原本有序，也会执行$O(n^2)$
• 非稳定排序：交换操作使排序失去了稳定性，无法维持原来相等元素的相对位置。

2. 冒泡排序【拥有稳定性】

选择排序三大问题：

• 不稳定，交换导致改变相同元素相对位置
• 时间复杂度与初始有序度无关，即便一开始是完全有序，时间复杂度还是$O(n^2)$
• 执行次数大概是$(n^2)/2$，无法优化

1. 优化稳定性

选择排序将最小值交换到最前面，

• 最小值放到前面这一步本身不会破坏稳定性，

• 将最前面的值放到最小值的位置，自然就破坏了最前面值原本的稳定性。

• 所以，我们还是将最小值放到最前面，但是最前面的值不再直接放到最小值位置，而是整体向后移动。

// 对选择排序进行第一波优化，获得了稳定性
void sort(vector<int>& nums) {int n = nums.size();int sortedIndex = 0;while (sortedIndex < n) {// 在未排序部分中找到最小值 nums[minIndex]int minIndex = sortedIndex;for (int i = sortedIndex + 1; i < n; i++) {if (nums[i] < nums[minIndex]) {minIndex = i;}}// 优化：将 nums[minIndex] 插入到 nums[sortedIndex] 的位置// 将 nums[sortedIndex..minIndex] 的元素整体向后移动一位int minVal = nums[minIndex];// 数组搬移数据的操作for (int i = minIndex; i > sortedIndex; i--) {nums[i] = nums[i - 1];}nums[sortedIndex] = minVal;sortedIndex++;}
}

获得了稳定性，但是执行效率降低了，因为变成了双层for循环外加一次for循环，执行次数远大于$n^2/2$。

第一次双层for循环找到最小值
第二次for循环将最小值插入，并且整体后移

2. 优化时间复杂度
继续优化时间复杂度，合并上面两次for循环，实现了冒泡排序的本质：倒序遍历n次，每次都边找最小值边排序，即交换逆序对

• n次倒序遍历nums[sortedIndex…]
• 如果发现了逆序对就交换顺序
• 这样nums[sortedIndex…]的最小值就是慢慢移动到nums[sortedIndex]
• 全程只交换相邻逆序对，完全不动相同元素，所以稳定排序。
• 冒泡排序，从尾部向头部冒泡

void sortVector<vector<int>& nums> {int n = nums.size();// sortedIndex前面都是有序的int sortedIndex = 0;	// n次遍历！每次把当前最小的值pop到最前面也就是sortedIndex = 0位置while (sortedIndex = 0) {  for (int i = n - 1; i > sortedIndex; i-- ) {// 如果发现一次逆序对(前>后)就交换if (nums[i - 1] > nums[i]) {// swap交换逆序对int tmp = nums[i];nums[i] = nums[i-1];nums[i-1] = tmp;}}// 成功把最小值pop到前面一次sortedIndex++; 										}
}

这个算法的名字叫做冒泡排序，因为它的执行过程就像从数组尾部向头部冒出水泡，每次都会将最小值顶到正确的位置。

3. 提前终止
还有个优化点，那就是选择排序和目前的冒泡排序都是与数组原始有序性无关的，即便已经有序，也会执行$O(n^2)$次，我们可以想办法检测有序性提前终止程序。
flag编程：用这个标记编程的思想，如果某次倒序遍历完全没有找到逆序对，没有发生swap，则说明已经有序，不需要继续执行程序！
只需要加一个bool值，记录每次倒序遍历是否发生swap即可！

void sortVector<vector<int>& nums> {int n = nums.size();int sortedIndex = 0;	while (sortedIndex = 0) {  // 设置flag, 初始化没有发生swapbool swapped = false; for (int i = n - 1; i > sortedIndex; i-- ) {if (nums[i - 1] > nums[i]) {int tmp = nums[i];nums[i] = nums[i-1];nums[i-1] = tmp;// 如果发生了swap，设为truebool swapped = true;}}// 如果某次遍历完全没有swap,说明已经有序，退出程序if (!swapped) break; sortedIndex++; 										}
}

3. 插入排序【逆向思维】【扑克牌抓牌】

对选择排序不稳定的问题，我们有一些解决办法了：

• 保住稳定性：我们提出了一次for循环找到最小值，最小值放在最前面，然后再一次for循环把其他元素都逐一往后排，保住了排序的稳定性；
• 冒泡排序：倒序遍历 + 交换逆序对 + flag编程提前终止
• 成功合并了for循环，还有其他方法把while里面的两个for优化成一个for循环么？

逆向思维：

• 前面两种算法都是在后面 nums[sortedIndex…] 中找到最小值，然后将其插入到 前面nums[sortedIndex] 的位置，这两步操作就是两次for循环。
• 反过来想，能不能在nums[0…sortedIndex-1] 这个部分有序的数组中，找到 nums[sortedIndex] 应该插入的位置，然后进行插入呢？
  • 有序数组 nums[0…sortedIndex-1] 找到应该插入的位置，很自然想到用二分查找，这样就可以把第一次for循环$O(n)$优化为$O(log(n))$
  • 但是找到后还得交换，又是一次for循环
  • 还不如继续用冒泡的思想，一边找一边换？

// 对选择排序进一步优化，向左侧有序数组中插入元素
// 这个算法有另一个名字，叫做插入排序
void sort(vector<int>& nums) {int n = nums.size();// 维护 [0, sortedIndex) 是有序数组int sortedIndex = 0;while (sortedIndex < n) { // 将 nums[sortedIndex] 插入到有序数组 [0, sortedIndex) 中// 依旧是倒序遍历，交换逆序对！for (int i = sortedIndex; i > 0; i++) {if (nums[i] < nums[i-1]) {int tmp = nums[i];nums[i] = nums[i-1];nums[i-1] = tmp;} else { // 到了该到的位置了！换不下去了！break;}}sortedIndex++;}

插入排序就像是打扑克，把新抓到的牌放到已经排好序的牌中：

1. 原地排序算法：空间复杂度
2. 时间复杂度依旧是$O(n^2)$，实际操作次数大约是$n^2/2$次
3. 稳定排序：只有在 nums[i] < nums[i - 1] 的情况下才会交换元素，所以相同元素的相对位置不会发生改变。
4. 与初始有序度强相关：
   • 初始有序度高，仅有个别元素逆序，则内层负责swap的for循环几乎不操作，时间复杂度接近$O(n)$；
   • 初始完全逆序，插入排序效率极低，每次都与nums[0…sortedIndex-1] 所有元素交换，总时间复杂度极为接近$O(n^2)$。
   • 插入排序的实际操作次数会小于冒泡排序的

4.

理解h有序数组：

• 间隔h位置，是有序的数组

希尔排序是基于选择排序进行优化的

• 插入排序的问题：上来就想一步到位，直接把乱序数组变成1有序数组
• 希尔的概念是不着急，先变成16有序数组，然后8有序数组，4，2，最后变成1有序数组，完成排序！

插入排序三步改动实现希尔排序：见代码

// 希尔排序本质：对h有序数组进行插入排序
// 逐步缩小h
void sort(vector<int>& nums) {int n = nums.size();// 设置生成函数 2^(k-1)// 即 h = 1，2，3，4，...int h = 1;while (h < n/2) {	// h放到最大h = 2 * h;}// 改动一：插入排序所有逻辑套在h的while循环中while (h >= 1) {// 改动二：sortedIndex 初始值设置为 h ，而不是1int sortedIndex = h;while (sortedIndex < n) {// 改动三：把比较和交换元素的步长设置为h，而不是相邻元素 // 依旧是倒序遍历，交换逆序对（相隔h）！// 原来是： for (int i = sortedIndex; i > 0; i--) {for (int i = sortedIndex; i >= h; i-=h) {if (nums[i] < nums[i-h]) { // 减1都换成减hint tmp = nums[i];nums[i] = nums[i-h];nums[i-h] = tmp;} else { // 到了该到的位置了！换不下去了！break;}}sortedIndex++;}// 按照递增函数的规则，缩小hh /= 2;}
}

• 时间复杂度终于低于$O(n^2)$
• 原地排序：空间复杂度 $O(1)$
• 不稳定排序，打乱了相同元素的顺序！

5. 快速排序【妙用二叉树前序位置】

6.

7.

8.

9.

10.

数据结构

链表题

数组题

双指针

滑窗

二分搜索基本框架

思路很简单，细节是魔鬼！
整型溢出在二分查找里面都不算事；
到底是给mid加一还是减一？
while 里面到底是 <= 还是 <?
要是没有正确理解细节，二分对我来说就是玄学算法！

二分查找问题常见的三个场景：

• 寻找一个数；
• 寻找左侧边界；
• 寻找右侧边界；
  并且深入细节：
• while 里面 是否要带等号？
• mid 是否 应该 +1？

计算 mid 需要防止溢出：

• left + (right - left) / 2
• 结果 其实与 (left + right) / 2 结果相同，但是有效防止了left right太大导致相加溢出的情况

二分查找的一个技巧：

• 不用else
• 把所有情况的else if 写清楚，展示所有细节

int binarySearch(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1;while (...) {int mid = left + (right - left) / 2;if (nums[mid] == target) {...} else if (nums[mid] < target) {left = ...} else if (nums[mid] > target) {right = ...}}
}

… 里面就是关键

寻找一个数字——最基本二分搜索

标准的二分搜索框架，搜索目标元素的索引，若不存在则返回 -1

class Solution {
public:// 标准的二分搜索框架，搜索目标元素的索引，若不存在则返回 -1int search(vector<int>& nums, int target) {int left = 0;// 注意int right = nums.size() - 1;while(left <= right) {int mid = left + (right - left) / 2;if(nums[mid] == target) {return mid;   } else if (nums[mid] < target) {// 注意left = mid + 1;} else if (nums[mid] > target) {// 注意right = mid - 1;}}return -1;}
};

细节一：为什么while循环的条件是 <= 而不是 < ？

• 因为初始化右指针right时，赋值是 n - 1，是最后一个元素索引，而不是 n；
• 搜索区间被定义为了一个闭区间 [left, right] ，而不是 [left, right) 左闭右开；
• 那写成闭区间搜索，何时停止搜索呢?
  • 能找到target的情况，当然就是 nums[mid] == target时；
  • 找不到target的情况，就需要搜索区间 [left, right] 为空的时候停止搜索，注意 [left, right] 当 left == right 时，搜索区间还有一个元素！所以是 left > right 时退出while循环，比如 left == right + 1 ，搜索区间 [right + 1, right] 此时才没有元素！
• 因此，while 的循环条件就是，left <= right ！
• 如果不小心把上面的写成 while (left < right) 那么显然就少了 [right , right] 这个搜索情况没检查

细节二：为什么是 left = mid + 1 ，right = mid - 1？
有的代码是 不加一减一的为啥这里是都加一减一？
这个很简单理解：
当我们知道mid处的值nums[mid] 根本不是我们要找的target！我们就没有必要留着mid这个位置了！
自然要去[mid+1, right] 或者[left, mid-1]寻找target了！
mid位置已经寻找过，没有，自然就是要去掉mid位置。

细节三：这样写的缺陷？
如果target在nums中不止只有一个！要寻找其左右边界，这个算法是做不到的！
比如说给你有序数组 nums = [1,2,2,2,3]，target 为 2，此算法返回的索引是 2，没错。但是如果我想得到 target 的左侧边界，即索引 1，或者我想得到 target 的右侧边界，即索引 3，这样的话此算法是无法处理的。

寻找左侧边界的二分搜索

函数签名：返回target的左侧边界索引，如果没有的话返回的是什么？

int left_bound(vector<int>& nums, int target) {
}

这次我用左闭右开 [left, right)

int left_bound(vector<int>& nums, int target) {int right = nums.size();  // 左闭右开 [ l, r )int left = 0;while (left < right) {   	// int mid = left + (right - left) / 2;if (nums[mid] == target) { // 即便是找到了target ，right = mid;         // 收缩上边界，继续往左找左边界		} else if (nums[mid] > target) {right = mid;			// 右开，[left, right)更新为[left, mid)} else if (nums[mid] < target) {left = mid + 1;			// 左闭，[left, right)更新为[mid+1, right)}}	// left == right 时退出循环！ x x t t t x x // 如果找到了target左边界，return left;
}

细节一：这里while 的循环条件没有等号了？
因为这次是左闭右开，初始化时：right = n，[left, right) 当left == right 时，搜索区间为空，退出搜索！

细节二：为什么是 left = mid + 1 和 right = mid？
还是因为左闭右开的搜索区间，[left, right) ，当 检查过 nums[mid] ，并且确定mid 不是我们要找的，下一步应该是去mid 左侧或者右侧的 左闭右开的区间搜索 [ left , mid) 不包含

• [ left ， mid) 不包含 mid
• [mid + 1，right) 才不含mid

细节三：为什么该算法能够搜索左侧边界？
上一题的解法就已经可以找到target，但是它的问题在于，只要找到一个target马上就返回，如果要找target的左边界，那就需要缩小搜索区间的上界right！

• 即便是找到了 ，即 nums[mid] == target
• 这时候，不返回结果，而是选择继续缩小上边界
• 也就是 right = mid ， 假设mid 左边还有 target！继续搜索[left, mid)
• 不断向左收缩，达到锁定左侧边界的目的。

细节四：target 不存在时返回什么？
如果 nums 中不存在 target 这个值，计算出来的这个索引含义是什么？如果我想让它返回 -1，怎么做？
**直接说结论：如果 target 不存在，搜索左侧边界的二分搜索返回的索引是大于 target 的最小索引。**举个例子，nums = [2,3,5,7], target = 4，left_bound 函数返回值是 2，因为元素 5 是大于 4 的最小元素。

变通一：在一个有序数组中，找到「小于 target 的最大元素的索引」？
// 比如说输入 nums = [1,2,2,2,3]，target = 2，函数返回 0，因为 1 是小于 2 的最大元素。
// 再比如输入 nums = [1,2,3,5,6]，target = 4，函数返回 2，因为 3 是小于 4 的最大元素。
答案就是left_bound(nums, target) - 1

int floor(vector<int>& nums, int target) {return left_bound(nums, target) - 1;
}

变通二：如果想让 target 不存在时返回 -1？
现在left_bound(nums, target)的代码是：

• 若target存在，返回左侧边界索引
• 若target不存在，返回第一个大于target的元素的索引
  关键：
• 分析，target 不存在也是我们搜索出来的结果，也就是不断收缩左右边界，最后逼近它可能存在的 区间，有三个可能：
• target 如果存在，在 nums 之中，即不在最前也不在最后边，这种情况，我们对比 找到的nums[left] 是否 就是我们要找的 target就行！
• 如果 target 比 nums都大？这时，left_bound 会返回 nums.size()，
• 如果 target 比 nums 都小? 这时，left_bound 会返回 -1，
  总结：不存在还分两种情况，索引越界即<0 或者 >= nums.size() 时直接返回 - 1；
  第二种情况是：找到了一个 left 在索引范围内，需要判断 找到的这个值 就是target 的左边界还是 比 target大的一个元素，target不存在

// 如果不存在 target 不返回 比其大的第一个 元素
int left_bound(vector<int>& nums, int target) {int right = nums.size();  // 左闭右开 [ l, r )int left = 0;while (left < right) {   	// int mid = left + (right - left) / 2;if (nums[mid] == target) { // 即便是找到了target ，right = mid;         // 收缩上边界，继续往左找左边界		} else if (nums[mid] > target) {right = mid;			// 右开，[left, right)更新为[left, mid)} else if (nums[mid] < target) {left = mid + 1;			}}	// 索引越界检查if (left < 0 || left >= nums.size()) {return -1;}// 检查nums[left] 是不是 targetreturn nums[left] == target ? left : -1;
}

提示：其实上面的 if 中 left < 0 这个判断可以省略，因为对于这个算法，left 不可能小于 0
// 你看这个算法执行的逻辑，left 初始化就是 0，且只可能一直往右走，那么只可能在右侧越界
// 不过我这里就同时判断了，因为在访问数组索引之前保证索引在左右两端都不越界是一个好习惯，没有坏处
// 另一个好处是让二分的模板更统一，降低你的记忆成本，因为等会儿寻找右边界的时候也有类似的出界判断

二分搜索最关键的一点就是 明确搜索区间！

当然也可以改为左右都闭的写法！
关键还是在于，即便是找到了target，也继续收缩右边界！

int left_bound(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1;// 搜索区间为 [left, right]while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] < target) {// 搜索区间变为 [mid+1, right]left = mid + 1;} else if (nums[mid] > target) {// 搜索区间变为 [left, mid-1]right = mid - 1;} else if (nums[mid] == target) { 	// 即便是找到了也继续收缩！！// 收缩右侧边界right = mid - 1;}}// 判断 target 是否存在于 nums 中// 如果越界，target 肯定不存在，返回 -1if (left < 0 || left >= nums.size()) {return -1;}// 判断一下 nums[left] 是不是 targetreturn nums[left] == target ? left : -1;
}

寻找右侧边界的二分查找

左闭右开写法：

• 关键点：即便是搜索到了target也不返回，而是收缩左边界！即 left = mid + 1!!
  即：

// 增大 left，锁定右侧边界
if (nums[mid] == target) {left = mid + 1;// 这样想: mid = left - 1
}

左闭右开的循环条件是 left <= right!
因为[left, right)， left == right 区间内还有一个元素，需要继续搜索
只有 left == right + 1时才退出循环！即便是已经确定mid就是要找的target！
left = mid + 1;
可以写成mid = left - 1
那么答案就要返回left - 1!

所以关键点：

• while 循环条件 有等号
• 收缩左边界，left = mid + 1
• 因为第二点，当mid就是target时有：mid = left - 1，返回target的索引就是left - 1!!

注意这些地方就可以写出搜索右侧边界的代码right_bound！

int right_bound(vector<int>& nums, int target) {int left = 0, right = nums.size();while (left < right) {int mid = left + (right - left) / 2;if (nums[mid] == target) {// 注意left = mid + 1;} else if (nums[mid] < target) {left = mid + 1;} else if (nums[mid] > target) {right = mid;}}// 注意return left - 1;
}

当target 不存在时返回的是什么呢？
当 target 不存在时，right_bound 返回值的含义

直接说结论，和前面讲的 left_bound 相反：如果 target 不存在，搜索右侧边界的二分搜索返回的索引是小于 target 的最大索引。

如果不存在target想改成返回-1也和前面类似“

// 计算出left - 1后
// 判断 target 是否存在于 nums 中
// left - 1 索引越界的话 target 肯定不存在
if (left - 1 < 0 || left - 1 >= nums.size()) {return -1;
}
// 判断一下 nums[left - 1] 是不是 target
return nums[left - 1] == target ? (left - 1) : -1;

也可以改为两端都闭的写法！

int right_bound(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1;while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] < target) {left = mid + 1;} else if (nums[mid] > target) {right = mid - 1;} else if (nums[mid] == target) {// 这里改成收缩左侧边界即可left = mid + 1;}}// 最后改成返回 left - 1if (left - 1 < 0 || left - 1 >= nums.size()) {return -1;}return nums[left - 1] == target ? (left - 1) : -1;
}

闭区间写法中 ，是当 left = right + 1时退出循环 即 right = left - 1时候退出！
而还是因为找到target时，要求继续收缩左边界：left = mid + 1
因此右侧边界位置是 mid = left - 1 = right

其实将搜索区间统一成两端都闭更好记忆！

总结一下：将逻辑进行统一

逻辑统一
梳理一下这些细节差异的因果逻辑：

第一个，最基本的二分查找算法：

因为我们初始化 right = nums.length - 1
所以决定了我们的「搜索区间」是 [left, right]
所以决定了 while (left <= right)
同时也决定了 left = mid+1 和 right = mid-1因为我们只需找到一个 target 的索引即可
所以当 nums[mid] == target 时可以立即返回

第二个，寻找左侧边界的二分查找：

因为我们初始化 right = nums.length
所以决定了我们的「搜索区间」是 [left, right)
所以决定了 while (left < right)
同时也决定了 left = mid + 1 和 right = mid因为我们需找到 target 的最左侧索引
所以当 nums[mid] == target 时不要立即返回
而要收紧右侧边界以锁定左侧边界

第三个，寻找右侧边界的二分查找：

因为我们初始化 right = nums.length
所以决定了我们的「搜索区间」是 [left, right)
所以决定了 while (left < right)
同时也决定了 left = mid + 1 和 right = mid因为我们需找到 target 的最右侧索引
所以当 nums[mid] == target 时不要立即返回
而要收紧左侧边界以锁定右侧边界又因为收紧左侧边界时必须 left = mid + 1
所以最后无论返回 left 还是 right，必须减一

对于寻找左右边界的二分搜索，比较常见的手法是使用左闭右开的「搜索区间」，我们还根据逻辑将「搜索区间」全都统一成了两端都闭，便于记忆，只要修改两处即可变化出三种写法：

int binary_search(vector<int>& nums, int target) {int left = 0, right = nums.size()-1; while(left <= right) {int mid = left + (right - left) / 2;if (nums[mid] < target) {left = mid + 1;} else if (nums[mid] > target) {right = mid - 1; } else if(nums[mid] == target) {// 直接返回return mid;}}// 直接返回return -1;
}int left_bound(vector<int>& nums, int target) {int left = 0, right = nums.size()-1;while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] < target) {left = mid + 1;} else if (nums[mid] > target) {right = mid - 1;} else if (nums[mid] == target) {// 别返回，锁定左侧边界right = mid - 1;}}// 判断 target 是否存在于 nums 中if (left < 0 || left >= nums.size()) {return -1;}// 判断一下 nums[left] 是不是 targetreturn nums[left] == target ? left : -1;
}int right_bound(vector<int>& nums, int target) {int left = 0, right = nums.size()-1;while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] < target) {left = mid + 1;} else if (nums[mid] > target) {right = mid - 1;} else if (nums[mid] == target) {// 别返回，锁定右侧边界left = mid + 1;}}// 由于 while 的结束条件是 right == left - 1，且现在在求右边界// 所以用 right 替代 left - 1 更好记if (right < 0 || right >= nums.size()) {return -1;}return nums[right] == target ? right : -1;
}

总结：

1、分析二分查找代码时，不要出现 else，全部展开成 else if 方便理解。把逻辑写对之后再合并分支，提升运行效率。

2、注意「搜索区间」和 while 的终止条件，如果存在漏掉的元素，记得在最后检查。

3、如需定义左闭右开的「搜索区间」搜索左右边界，只要在 nums[mid] == target 时做修改即可，搜索右侧时需要减一。

4、如果将「搜索区间」全都统一成两端都闭，好记，只要稍改 nums[mid] == target 条件处的代码和返回的逻辑即可，推荐拿小本本记下，作为二分搜索模板。

最后我想说，以上二分搜索的框架属于「术」的范畴，如果上升到「道」的层面，二分思维的精髓就是：通过已知信息尽可能多地收缩（折半）搜索空间，从而增加穷举效率，快速找到目标。

lc.34 排序数组中查找元素的第一个和最后一个位置！

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

二维搜索应用泛化

也就是什么问题可以用到二分搜索算法？

什么问题可以运用二分搜索算法技巧？

首先，你要从题目中抽象出一个自变量 x，一个关于 x 的函数 f(x)，以及一个目标值 target。

同时，x, f(x), target 还要满足以下条件：

1、f(x) 必须是在 x 上的单调函数（单调增单调减都可以）。

2、题目是让你计算满足约束条件 f(x) == target 时的 x 的值。

上述规则听起来有点抽象，来举个具体的例子：

给你一个升序排列的有序数组 nums 以及一个目标元素 target，请你计算 target 在数组中的索引位置，如果有多个目标元素，返回最小的索引。

这就是「搜索左侧边界」这个基本题型，解法代码之前都写了，但这里面 x, f(x), target 分别是什么呢？

我们可以把数组中元素的索引认为是自变量 x，函数关系 f(x) 就可以这样设定：

// 函数 f(x) 是关于自变量 x 的单调递增函数
// 入参 nums 是不会改变的，所以可以忽略，不算自变量
int f(int x, vector& nums) {
return nums[x];
}

其实这个函数 f 就是在访问数组 nums，因为题目给我们的数组 nums 是升序排列的，所以函数 f(x) 就是在 x 上单调递增的函数。

最后，题目让我们求什么来着？是不是让我们计算元素 target 的最左侧索引？

是不是就相当于在问我们「满足 f(x) == target 的 x 的最小值是多少」？

画个图，如下：

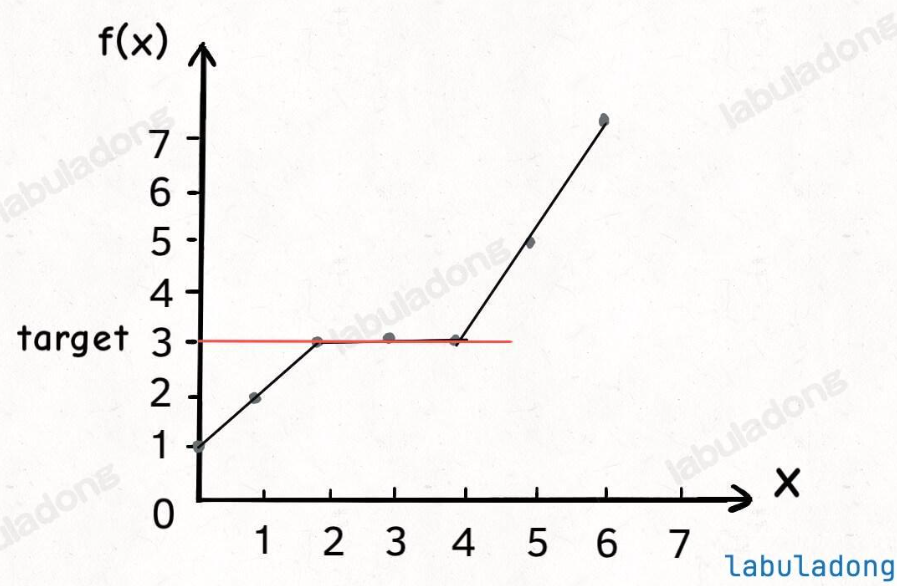
如果遇到一个算法问题，能够把它抽象成这幅图，就可以对它运用二分搜索算法。

二分搜索代码框架

想要运用二分搜索解决具体的算法问题，可以从以下代码框架着手思考：

// 函数 f 是关于自变量 x 的单调函数
int f(int x) {// ...
}// 主函数，在 f(x) == target 的约束下求 x 的最值
int solution(vector<int>& nums, int target) {if (nums.size() == 0) return -1;// 问自己：自变量 x 的最小值是多少？int left = ...;// 问自己：自变量 x 的最大值是多少？int right = ... + 1;while (left < right) {int mid = left + (right - left) / 2;if (f(mid) == target) {// 问自己：题目是求左边界还是右边界？// ...} else if (f(mid) < target) {// 问自己：怎么让 f(x) 大一点？// ...} else if (f(mid) > target) {// 问自己：怎么让 f(x) 小一点？// ...}}return left;
}

具体来说，想要用二分搜索算法解决问题，分为以下几步：

1、确定 x, f(x), target 分别是什么，并写出函数 f 的代码。

2、找到 x 的取值范围作为二分搜索的搜索区间，初始化 left 和 right 变量。

3、根据题目的要求，确定应该使用搜索左侧还是搜索右侧的二分搜索算法，写出解法代码。

下面用几道例题来讲解这个流程。

lc875. 爱吃香蕉的珂珂

珂珂喜欢吃香蕉。这里有 n 堆香蕉，第 i 堆中有 piles[i] 根香蕉。警卫已经离开了，将在 h 小时后回来。

珂珂可以决定她吃香蕉的速度 k （单位：根/小时）。每个小时，她将会选择一堆香蕉，从中吃掉 k 根。如果这堆香蕉少于 k 根，她将吃掉这堆的所有香蕉，然后这一小时内不会再吃更多的香蕉。

珂珂喜欢慢慢吃，但仍然想在警卫回来前吃掉所有的香蕉。

返回她可以在 h 小时内吃掉所有香蕉的最小速度 k（k 为整数）。

示例 1：

输入：piles = [3,6,7,11], h = 8
输出：4
珂珂每小时最多只能吃一堆香蕉，如果吃不完的话留到下一小时再吃；如果吃完了这一堆还有胃口，也只会等到下一小时才会吃下一堆。

他想在警卫回来之前吃完所有香蕉，让我们确定吃香蕉的最小速度 K。函数签名如下：

int minEatingSpeed(vector<int>& piles, int H);

1、确定 x, f(x), target 分别是什么，并写出函数 f 的代码。
自变量 x 是什么呢？回忆之前的函数图像，二分搜索的本质就是在搜索自变量。

所以，题目让求什么，就把什么设为自变量，珂珂吃香蕉的速度就是自变量 x。

那么，在 x 上单调的函数关系 f(x) 是什么？

显然，吃香蕉的速度越快，吃完所有香蕉堆所需的时间就越少，速度和时间就是一个单调函数关系。

所以，f(x) 函数就可以这样定义：

若吃香蕉的速度为 x 根/小时，则需要 f(x) 小时吃完所有香蕉。

代码实现如下：

// 定义：速度为 x 时，需要 f(x) 小时吃完所有香蕉
// f(x) 随着 x 的增加单调递减
int f(vector<int>& piles, int x) {int hours = 0;int n = piles.size();// for (int i = 0; i < n; i++) {}return hours;
}

前缀和

差分

队列/栈

实现队列/栈

经典

单调栈

单调队列

二叉树&递归

二叉树核心框架

递归 + 遍历

递归 + 分解

层序遍历

数据结构设计

LRU

LFU

经典设计

图论

图结构通用代码

图的逻辑结构

图的逻辑结构构成：

• 节点vertex
• 边edge

图节点的逻辑结构：

// 图节点实现
class Vertex {
public:int id;std::vector<Vertex*> neighbors;
};

图其实就是多叉树：

// 多叉树节点结构
class TreeNode {
public:int val;std::vector<TreeNode*> children;
};

以上只是逻辑上的构成，实际应用中，很少用这个 Vertex类。

邻接表和邻接矩阵实现图结构

比如一幅图：

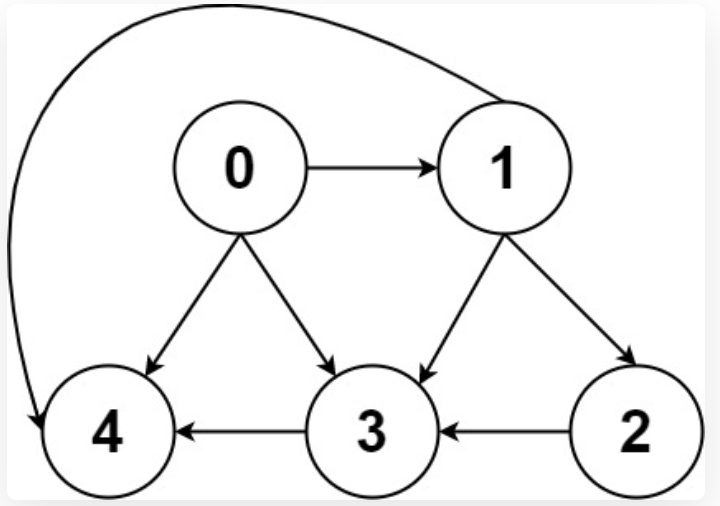
有两种表示方法：

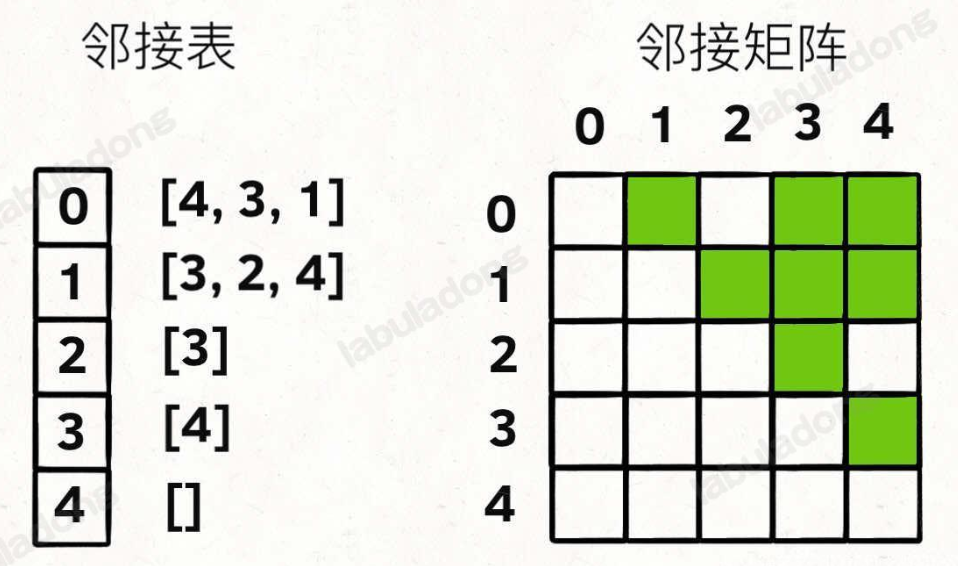
邻接表很直观，我把每个节点 x 的邻居都存到一个列表里，然后把 x 和这个列表映射起来，这样就可以通过一个节点 x 找到它的所有相邻节点。

邻接矩阵则是一个二维布尔数组，我们权且称为 matrix，如果节点 x 和 y 是相连的，那么就把 matrix[x][y] 设为 true（上图中绿色的方格代表 true）。如果想找节点 x 的邻居，去扫一圈 matrix[x][…] 就行了

// 邻接表：graph[x] 存储 x 指向的 所有邻居节点
vector<vector<int>> graph;// 邻接矩阵：matrix[x][y] 记录 x 是否有 一条指向 y 的边
vector<vector<bool>> matrix;

分别适用于不同场景
分析两种存储方式的空间复杂度，对于一幅有 V 个节点，E 条边的图，邻接表的空间复杂度是
O
(
V
+
E
)
O(V+E)，而邻接矩阵的空间复杂度是
O
(
V
2
)
O(V
2
)。

所以如果一幅图的 E 远小于 V^2（稀疏图），那么邻接表会比邻接矩阵节省空间，反之，如果 E 接近 V^2（稠密图），二者就差不多了。

在后面的图算法和习题中，大多都是稀疏图，所以你会看到邻接表的使用更多一些。

邻接矩阵的最大优势在于，矩阵是一个强有力的数学工具，图的一些隐晦性质可以借助精妙的矩阵运算展现出来。不过本文不准备引入数学内容，所以有兴趣的读者可以自行搜索学习。

这也是为什么一定要把图节点类型转换成整数 id 的原因，不然的话你怎么用矩阵运算呢？

环检测

拓扑排序

二分图判定

并查集

最小生成树

Dijkstra 最短路径算法

DFS / 回溯

BFS

动态规划

动归核心框架

子序列问题

背包问题

0-1背包问题

物品有两个属性：重量wt 和 价值 val
背包有两个属性：载重W 和 容量N（最多装几个物品）
问：最多能装多少价值的东西？

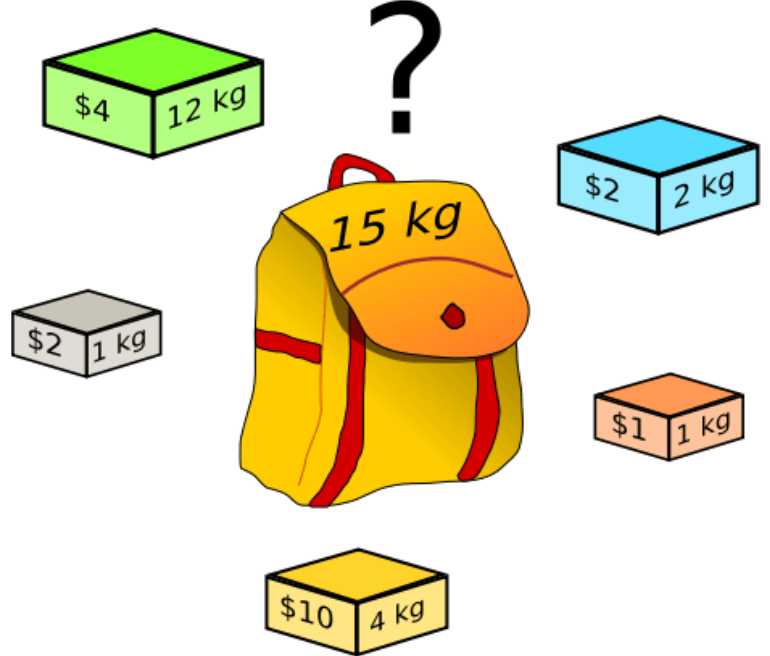
解法：动态规划
第一步：确定「状态」和「选择」
从背包的状态和物品的状态出发：

• 状态：即描述当前问题的局面（即背包的状态和物品的状态，不涉及选择），从「可选择的前i个物品 」「可用的容量 」；

• 选择：对于每件商品，选择「装进背包」或者「不装进背包」；

  自顶而下的代码框架：

  for 状态1 in 状态1的所有取值：for 状态2 in 状态2的所有取值：for ...dp[状态1][状态2][...] = 择优(选择1，选择2...)
  

第二步：定义dp数组， 某个状态的最优解

• 从状态出发：涉及两个东西的状态，所以需要二维数组dp[ ][ ]；

• dp[ i ][ w ] 定义为：前 i 个物品情况下（ 选择了某些物品，背包容量剩余 w ）此时，选择i 以及 w的情况，价值最大为dp[i][w]；

• 例如： dp[3][5] = 6，表示：对于给定的一堆物品，一个背包，若限制从前三个物品选，当选了某些东西，容量为5时最优，价值为6；

• base case：dp[0][…] = dp[][0] = 0，物品数为0或者背包空间为0时，就是base case，为0；

  // 注意，最多N个物品，最大W的容量
  int[][] dp[N][W];
  dp[0][...] = 0;
  dp[...][0] = 0;
  for i in [1...N]:for w in [1...W]:dp[i][w] = max {把物品 i 放进背包不放 i}
  return dp[N][W];
  

第三步：根据「选择」，思考状态转移的逻辑

从dp定义出发：dp[i][w] 表示：对于前 i 个物品（从 1 开始计数），当前背包的容量为 w 时，这种情况下可以装下的最大价值是 dp[i][w]。
关键的选择是：

• 如果没有把第i个物品放入背包（w没有变）：dp[i][w]直接继承dp[i-1][w]，dp[i][w] = dp[i-1][w]
• 如果把第i个物品放入背包：dp[i][w] = val[i] + dp[i-1][W-wt[i-1]];(要在剩余容量的限制下，在前i-1个里面挑选，求最大值，也就是dp[i-1][W-wt[i-1]])

for i in [1..N]:for w in [1..W]:dp[i][w] = max(dp[i-1][w],dp[i-1][w - wt[i-1]] + val[i-1])
return dp[N][W]

最后一步：边界条件处理

#include <cassert>
// W 背包限重，wt[]，val[]
int knapsack(int W, vector<int>& wt, vector<int>& val) {int N = val.size();// 定义dp 并直接初始化0// dp[i][w] 限制前i个可选 + 限重w 时的最大价值vector<int> dp(N + 1, vector<int>(W + 1));for (int i = 1; i <= N; i++) { 			// 状态1：for (int w = 1; w <= W; w++) {		// 状态2：// 注意处理，可能有的物品wt[i]重量大于当前限重w// 则直接跳过dp[i][w]?那只能说明不能选i// 强制不选i，即dp[i][w] = dp[i-1][w]if (wt[i] > w) {dp[i][w] = dp[i-1][w];}else { dp[i][w] = max(val[i] + dp[i-1][w-wt[i]] // 选择1dp[i-1][w]				 // 选择2);}}}return dp[N][W];
}

474. 一和零

vector<int> dp(N+1, vector<int>(W + 1));
dp[i][w]	// 只能【选前i个物品】，【限重w】情况下，最大价值为dp[i][w]

dp[i][j][k]	// 只能【选前i个物品】，【0 最大限制j个】【1 最大限制k个】情况下，最大数量为dp[i][j][k]

class Solution {
public:int findMax(vector<string>& strs, int m, int n) {// 定义dp：dp[][][]// 如果只能选前i个元素，最多选j个0，最多选k个1；// 可以装的最大字符串数为 dp[i][j][k]// 注意三维数组的定义方式l = strs.size();vector<vector<vector<int>>> dp(l + 1, vector<vector<int>>(m + 1, vector<int>(n + 1, 0)));// base case：dp[0][...][...] = 0 没有任何字符串可选时，最大可装的数量是0// 从 base case 开始状态转移 ， 从 1 到 nfor (int i = 1; i <= l; i++) {// 注意存在一个索引偏移，dp[i][][] 的i是第i个的意思，对应到strs 的当前char索引是i-1string curStr = strs[i - 1];// 统计当前curStr(物品)的0数量和1数量(重量)int zeroCount = 0;int oneCount = 0;for (char c : curStr) {if (c == '0') zeroCount++;else oneCount++;}// 根据要不要选 curStr 进行状态转移for (int j = 0; j <= m;j++) {for (int k = 0; k <= n;k++) {// 检查当前物品curStr的重量zeroCount oneCount是否小于背包容量限制为j和kif (j >= zeroCount && k >= oneCount) {dp[i][j][k] = max(dp[i - 1][j][k],1 + dp[i - 1][j - zeroCount][k - oneCount]										);} else {					// 背包容量不足时，强制选择不放curStr！dp[i][j][k] = dp[i - 1][j][k];	// }}} }// return dp[l][m][n];}
};

1262. 可以被3整除的最大和

// 定义dp
dp = vector<int>(nums.size());

class Solution {
public:int maxSumDivThree(vector<int>& nums) {// 定义：nums[0..i] 中，和 3 相除余数为 j 的最大和是 dp[i][j]// 3 is dp[i][j]int n = nums.size();// dp[0][0/1/2]要作为base case，所以总共有n+1个情况vector<vector<int>> dp(n + 1, vector<int>(3, INT_MIN));// base casedp[0][0] = 0;dp[0][1] = INT_MIN;dp[0][1] = INT_MIN;// 状态转移方程：根据第i个数字nums[i]以及前i-1个数字的余数情况dp[i-1][1/2/3]// 来推导前i个数字的余数情况 dp[i][0/1/2] for (int i = 1; i <= nums; i++) {int curNum = nums[i - 1]; if (curNum % 3 == 0) {	// 当前元素curNum余数0，则前面元素和余数是多少，加上curNum之后还是多少，就看要不要加curNum【选择】dp[i][0] = max(curNum + dp[i - 1][0], dp[i - 1][0]);dp[i][1] = max(curNum + dp[i - 1][1], dp[i - 1][1]);dp[i][2] = max(curNum + dp[i - 1][2], dp[i - 1][2]);} else if (curNum % 3 = 1) { 	// 选不选余数为1的curNum？dp[i][0] = max(curNum + dp[i - 1][2], dp[i - 1][0]);dp[i][1] = max(curNum + dp[i - 1][0], dp[i - 1][1]);dp[i][2] = max(curNum + dp[i - 1][1], dp[i - 1][2]);} else { // curNum余数是2dp[i][0] = max(curNum + dp[i - 1][1], dp[i - 1][0]);dp[i][1] = max(curNum + dp[i - 1][2], dp[i - 1][1]);dp[i][2] = max(curNum + dp[i - 1][0], dp[i - 1][2]);		}}// 最后返回前i个元素的能被3整除最大和，即余数为0，dp[n][0]return dp[n][0];}
};

1235. 规划兼职工作

这次物品变成了不同的工作，每份工作有开始时间、结束时间、以及对应的价值，收益。
当然不可能分身，所以同一个时刻只能做一份工作，返回最大收益。
这也是0-1的变种问题：
0-1的状态是【前i个物品】【限重w】情况下，【选择】选不选当前的物品，使得当前价值最大；
这里的物品就是工作，工作有【开始时间】【结束时间】【收益】三个属性，打包到一起，【选择】选不选当前的工作，使得收益最大。
状态是：【前i个工作可选】？直接用endTime作为可选时间吧！

class Solution {
public:int jobScheduling(vector<int>& startTime, vector<int>& endTime, vector<int>& profit) {// 物品的三个属性打包到一起，方便排序int n = profit.size();vector<vector<int>> jobs(n, vector<int>(3));for (int i = 0; i < n;i++) {jobs[i] = {startTime[i], endTime[i], profit[i]};}// 用sort(起始，结束（开区间）， 排序规则 )；按end时间排序sort(jobs.begin(), jobs.end(), [](const vector<int> a, vector<int> b) {return a[1] < b[1];});// 至此已经按照一定顺序排列好了 “物品”map<int, int> dp;for (const auto& job : jobs) {// 提取出job的三个属性  int begin = job[0];int end = job[1];int value = job[2];// 进行选择，穷举所有选择dp[end] = max(// 选当前job，收益增加value，但是[begin, end)这段时间被占用了！// [begin, end)时间段内的工作都不行，[0,begin)内的任务可以// 用二分手段查找第一个结束时间大于等于begin的dp结果：dp.upper_bound(begin)// 这个的前一个prev就是不在[begin, end)区间内的选择的最大收益// 最后一个键 <= begin 的元素迭代器// dp<int, int> 第一个元素键是截至end ： 第二个元素值是收益value + prev(dp.upper_bound(begin))->second,// 不选当前job，则当前job[end]的值直接继承上一个end的值(保存现有最大值)dp.rbegin()->second; // rbegin()指向容器最后一个元素);}return dp.rbegin()->second;}
};

子集背包问题——LC.416 分割等和子集

输入一个只包含正整数的非空数组 nums，请你写一个算法，判断这个数组是否可以被分割成两个子集，使得两个子集的元素和相等。
比如说输入 nums = [1,5,11,5]，算法返回 true，因为 nums 可以分割成 [1,5,5] 和 [11] 这两个子集。
如果说输入 nums = [1,3,2,5]，算法返回 false，因为 nums 无论如何都不能分割成两个和相等的子集。

这个问题看起来和背包没啥关系啊？
0-1背包问题：求出【可装载重量W】【N个物品（每个物品价值v，重量w）】情况下，求出背包可装载最大价值。
分割子集要求：判断能否分割成两个和相等的子集，实际上，如果有一个子集可以凑成sum/2，另一半必然就是sum/2呀！
所以问题转化成了，背包【可装载重量 = sum/2】【N个物品（每个物品有重量nums[I]）】，问能不能恰好装满背包。

解法：
第一步：明确【状态】和【选择】

• 状态：跟0-1背包一样的，【可选择的物品】【背包当前容量】
• 选择：当前物品【装】【不装】

第二步：dp数组定义？base case？

• dp[i][j] = x：对于前i个物品可选（i从1开始计数？）， 背包容量j时，x为true表示可以装满，false表示不能恰好装满
• base case：没有物品可选时，dp[0][…] = 0；容量为0时，天然装满dp[…][0] = true；
• 最终返回的：N个物品时，能不能刚好凑到sum/2，return dp[N][sum/2]
• 举例：dp[4][9] 若只在前4个物品选择，有一种方案能够恰好把容量9的背包装满；或对于这道题，若只在前4个数字选择，存在一个子集的和为9；

第三步：根据【选择】分析状态转移的逻辑
也就是装不装第i个物品的问题（）：

• 不装：直接继承dp[i-1][j]
• 装：取决于dp[i-1][j - nums[i]]，如果装了第 i 个物品，就要看背包的剩余重量 j - nums[i-1] 限制下是否能够被恰好装满。如果 j - nums[i-1] 的重量可以被恰好装满，那么只要把第 i 个物品装进去，也可恰好装满 j 的重量；否则的话，重量 j 肯定是装不满的。

注意点：

• 上述分析都是第i个物品，所以与真实的nums索引差1
• 和为奇数的时候，必不可分
• 第i个物品（索引为i-1）的重量（nums[i - 1]） 大于背包总容量j时候，强制选择不装，装不了！

class Solution {
public:	bool canPartition(vector<int>& nums) {// 求sumint sum = 0;for (int num : nums) sum += num;// sum 为奇数，直接falseif (sum % 2 != 0) return false;// sum 偶数，继续int W = sum / 2;	// 定义dp[i][j]： i范围是0~n，j范围是0~Wint n = nums.size();vector<vector<int>> dp(n + 1, vector<int>(w + 1, false));// base case：初始化dp[0...n][0] = turefor (int i = 0; i >= n; i++) {dp[i][0] = true;			}// 状态转移：前提背包容量够， 且注意索引for (int i = 1; i <= n;i++) {	// 第i个选不选，索引是nums[i-1]选不选for (int j = 1; j <= W; j++) {	//// 如果 容量j 是足够的if (j >= nums[i - 1]) {// 装还是不装？dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i - 1]];} else {	// 容量不够,肯定是装不了第i个物品 nums[i - 1]dp[i][j] = dp[i - 1][j];}}}// 返回return dp[n][W];}
};

优化空间复杂度，因为这道题的dp[i][j] 全靠上一行 dp[i - 1][…]转化过来！
之前的元素都不会在用，不用保存所有的行！

class Solution {
public:	bool canPartition(vector<int>& nums) {// 求sumint sum = 0;for (int num : nums) sum += num;// sum 为奇数，直接falseif (sum % 2 != 0) return false;// sum 偶数，继续int W = sum / 2;	// 定义dp[i][j]： i范围是0~n，j范围是0~Wint n = nums.size();// vector<vector<int>> dp(n + 1, vector<int>(w + 1, false));vector<int> dp(W + 1, false);// base case：初始化dp[0...n][0] = ture 即dp[0] = true// for (int i = 0; i >= n; i++) dp[i][0] = true;dp[0] = true;// 状态转移：前提背包容量够， 且注意索引for (int i = 0; i < n; i++) {	// 第i个选不选，索引是nums[i-1]选不选for (int j = 1; j <= W; j++) {	//// 如果 容量j 是足够的if (j >= nums[i]) {// 装还是不装？dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i - 1]];}}}}// 返回// return dp[n][W];return dp[W];}
};

这段代码和之前的解法思路完全相同，只在一行 dp 数组上操作，i 每进行一轮迭代，dp[j] 其实就相当于 dp[i-1][j]，所以只需要一维数组就够用了。
唯一需要注意的是 j 应该从后往前反向遍历，因为每个物品（或者说数字）只能用一次，以免之前的结果影响其他的结果。
至此，子集切割的问题就完全解决了，时间复杂度O(n*sum)，空间复杂度
这句话没读懂啊，为啥会影响之前的其他结果？
为啥原来二维数组不用反向遍历？二维数组不能反过来遍历吧，前一个值都没有算出来，反过来不就不能利用上一个计算出来的值了吗？

chase4ever
Tokics
2023-04-19
这个要慢慢品，我理解了好久才悟到。

为什么不能正向遍历？因为外层遍历的是物品，0-1背包问题，一个物品只能选择一次，就是说，如果j正向遍历，容量从小到大可能多次选择这个品。
2.反向遍历，前面的数据都没计算，为什么j反向遍历正确？ 因为在计算dp[i][j]的时候，使用的是dp[i-1][j-v]的数据，即：只考虑0~i-1这么多物品的情况下的结果。这些都是完全计算过了的，反向遍历没有问题，且，反向遍历可以保证在j之前的容量里，一定没有考虑过这个物品。也就是说，当前可以决策是否装入i这个物品，是因为在这之前的容量没有考虑过是否装入i，保证i只能最多装入1次

子集背包问题——最后一块石头的重量II

有一堆石头，用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。

每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：

如果 x == y，那么两块石头都会被完全粉碎；
如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。
最后，最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下，就返回 0。

这道题完全就是分割子集的变形题，每次碰碎出两块石头，得到y-x！要求出最后剩余的石头的最小值，分割子集问题中要找出是否存在两个相等子集，
举上一题的例子：
比如说输入 nums = [1,5,11,5]，算法返回 true，因为 nums 可以分割成 [1,5,5] 和 [11] 这两个子集。
如果说输入 nums = [1,3,2,5]，算法返回 false，因为 nums 无论如何都不能分割成两个和相等的子集。
这里 nums = [1,5,11,5]，这里 11 碰 1 得到 10 ，10 碰 5 得到 5， 5 碰 5，最后是0；
nums = [1,3,2,5]，这里 5 碰了 1 得到 4，4 碰了 2 得到 2， 2 碰 3 得到 1；

其实就是分割子集，使得子集的差最小，也就是使得两个子集的重量和都尽量接近sum/2！

所以问题转换成了背包问题：
给定容量sum/2的背包，若干石头stones，问背包能装下的最大重量maxWeight是？则一堆重量和是maxWeight，另外一堆重量和（sum - maxWeight）是最后返回（sum - maxWeight） - maxWeight；这就是消除不掉的石头的重量和！

所以

• dp[i][j] 定义：仅可以选择前i个石头，容量是j情况下，装的最大重量dp[i][j]
• base case ：
  • dp[0][…] = 0
  • dp[…][0] = 0
• 状态转移：选不选第i个（索引变换）石头？
  • 石头巨大，超容量j：强制不选，继承上个值
  • 可选可不选 第i个石头，stone[i - 1]：
    • 选stone[i - 1]： stone[i - 1] + dp[i ][j - stone[i - 1]]
    • 不选：继承

class Solution {
public:int lastStoneWeightII(vector<int>& stones) {// 计算 sumint sum = 0;for (int stone : stones) sum += num;// 定义dp[i][j]：前i个石头可选，背包容量j 情况下，最多多重？  // i范围0~n 长度n+1， j范围0~W 长度W+1int n = stones.size(), W = sum / 2; vector<vector<int>> dp(n + 1, vector<int>(W + 1, 0));// base case：已经初始化！for (int i = 1; i <= n; i++) {int curStone = stones[i - 1];	// 索引问题for (int j = 1; j <= W; j++) {if (j < curStone) {dp[i][j] = dp[i - 1][j];} else {dp[i][j] = max(dp[i - 1][j],curStone + dp[i - 1][j - curStone]);}}}int maxWeight = dp[n][W];return sum - maxWeight * 2;}
};

完全背包问题——零钱兑换II

给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。

请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。

假设每一种面额的硬币有无限个。

输入：amount = 5, coins = [1, 2, 5]
输出：4
解释：有四种方式可以凑成总金额：
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1

很容易看出也是个背包类型的问题，跟前面最大的区别就是物品数量无限，称为完全背包问题。

第一步：确定状态和选择
状态：

• 背包的容量
• 可选择的物品
  选择：
• 装进背包
• 不装进背包
  动归框架：

for 状态1 in 状态1的所有取值：for 状态2 in 状态2的所有取值：for ...dp[状态1][状态2][...] = 计算(选择1，选择2...)

第二步：定义dp，要能从子问题推出新问题的dp！
从题意：求解凑出某个金额amout的方案数量，并且有两个状态可选择的物品和凑的金额
定义dp[i][j] : 若只能选前i种（注意！这里换成了“种”）物品（不限制数量，可重复），当容量j时，有dp[i][j]种方法可以填满背包容量j
换成这道题背景：
若只使用 coins 中的前 i 个（i 从 1 开始计数）硬币的面值，若想凑出金额 j，有 dp[i][j] 种凑法
base case ：

• dp[0][…] = 0；这一步很好想，没有选择，则方案必然为0
• dp[…][0] = ？；目标金额是0呢？什么都不做就已经完成目标金额，什么都不做是唯一的一个方案！dp[…][0] = 1；
  最终返回什么：return dp[n][amount]

伪代码：

int dp[N+1][amount+1]
dp[0][..] = 0
dp[..][0] = 1for i in [1..N]:for j in [1..amount]:把物品 i 装进背包,不把物品 i 装进背包
return dp[N][amount]

第三步：根据选择，思考动态转移

dp[i][j] 是「共有多少种凑法」
是只有前i“种”选择
选择：

• 如果我们不把第i种物品放入背包：不使用coins[i - 1]这种硬币，那么凑出面额j的方法数为dp[i - 1][j]
• 如果我们把第i种物品放入背包：即使用coins[i - 1]这种硬币，那么我们要关心的是如何凑出j - coins[i - 1]， 那么 dp[i][j] = dp[i][j - coin[i - 1]] 注意这里不是i - 1！而是用的同样i时的 容量更小的时候的dp[i][j - coin[i - 1]]
• 然后把选不选两种选择的方案数量！加到一起就是 总的方案数量！dp[i][j] = dp[i - 1][j] + dp[i][j - coins[i - 1]]

Note

有的读者在这里可能会有疑问，不是说可以重复使用硬币吗？那么如果我确定「使用第 i 个面值的硬币」，我怎么确定这个面值的硬币被使用了多少枚？简单的一个 dp[i][j-coins[i-1]] 可以包含重复使用第 i 个硬币的情况吗？

对于这个问题，建议你再仔回头细阅读一下我们对 dp 数组的定义，然后把这个定义代入 dp[i][j-coins[i-1]] 看看：

若只使用前 i 个物品（可以重复使用），当背包容量为 j-coins[i-1] 时，有 dp[i][j-coins[i-1]] 种方法可以装满背包。

看到了吗，dp[i][j-coins[i-1]] 也是允许你使用第 i 个硬币的，所以说已经包含了重复使用硬币的情况

class Solution {
public:int change(int amount, vector<int>& coins) {// 定义dp[i][j]int n = coins.size();vector<vector<int>> dp(n + 1, vector<int>(amount + 1, 0));// base case：dp[][0]for (int i = 0; i <= n; i++) dp[i][0] = 1;// for (int i = 1; i <= n;i++) {int curCoin = coins[i - 1];for (int j = 1; j <= amount; j++) {if (j < curCoin) {dp[i][j] = dp[i - 1][j];} else {dp[i][j] = dp[i - 1][j] + dp[i][j - curCoin];				}		}}return dp[n][amount];}
};

这道题只用到了，最近的两行状态dp！
思考如何空间压缩？如何记忆化搜索实现时间复杂度优化？

背包问题变体——494.目标和

打家劫舍

股票问题

贪心算法

数学

位操作

位操作是直接对整数的二进制位（0 或 1）进行运算的操作，是计算机底层数据处理的基础方式。它通过特定运算符对二进制位进行逻辑或移位处理，具有运算速度快（CPU 直接支持）、内存占用少等特点，广泛用于底层编程、算法优化、数据压缩等场景。

位运算核心优势：

• 效率极高：位运算直接在 CPU 层面执行，比加减乘除等运算更快。
• 节省空间：可用二进制位表示多个状态（如用 1 个字节存储 8 个布尔值）。
• 功能独特：特定问题，状态压缩、加密、奇偶判断等

常见应用场景

• 算法优化（如计算汉明重量、判断 2 的幂次方）。
• 数据加密（如异或加密）。
• 嵌入式编程（操作硬件寄存器）。
• 状态压缩（用二进制位表示多个开关状态）。

核心运算符

1. 与（&）：两个位都为 1 时，结果为 1；否则为 0。
   例：5（101） & 3（011） = 1（001）
2. 或（|）：两个位中至少有一个为 1 时，结果为 1；否则为 0。
   例：5（101） | 3（011） = 7（111）
3. 非（~）：将位 0 变为 1，1 变为 0（注意符号位处理，不同语言有差异）。
   例：~5（000…0101） = …11111010（取决于整数位数）
4. 异或（^）：两个位不同时（一个 0 一个 1），结果为 1；相同则为 0。
   例：5（101） ^ 3（011） = 6（110）
5. 左移（<<）：将二进制位向左移动指定位数，右侧补 0。
   例：5（101） << 1 = 10（1010）（相当于 ×2）
6. 右移（>>）：将二进制位向右移动指定位数，左侧补符号位（正数补 0，负数补 1）。
   例：5（101） >> 1 = 2（10）（相当于 ÷2 取整）

环形数组的位运算优化：index & (arr.length - 1)

1. 环形数组的常规实现：模运算 % 取余

环形数组需模拟 “头尾相接” 的循环遍历，常规做法是用模运算（取余运算）%计算索引：

• 当index递增时，index % arr.length可循环获取数组元素
• 示例（数组[1,2,3,4]）：
• (sizeof(arr) / sizeof(int) == 数组长度 arr.length

int arr[] = {1, 2, 3, 4};
int index = 0;
while (true) {// (sizeof(arr) / sizeof(int) == 数组长度 4cout << arr[index % (sizeof(arr) / sizeof(int))] << endl;index++;
}
// 输出：1,2,3,4,1,2,3,4,1,2,3,4...

缺点：模运算%对计算机而言是较昂贵的操作，性能较低。

2. 优化方案：&运算替代%

技巧题

补充高频题

42.接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

接下来由浅入深介绍暴力解法 -> 备忘录解法 -> 双指针解法，在 O(N) 时间 O(1) 空间内解决这个问题。

解法一：暴力

简化问题的方法：

• 从问题局部开始思考
• 写出简单粗暴的解法
• 逐步优化

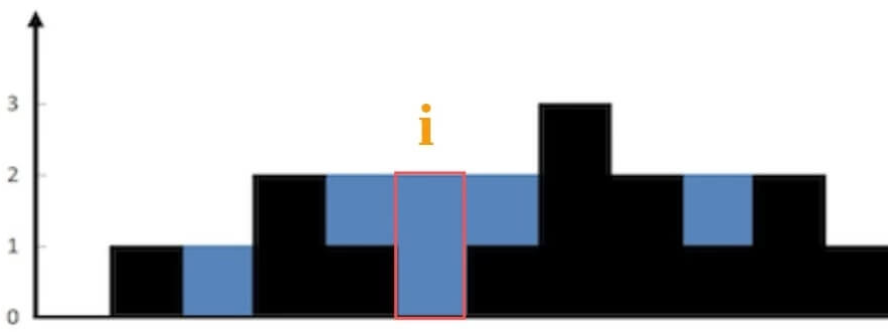
比如先放弃整体思考，而是思考某个位置i能装多少水：

• 这个位置能装2格水，因为height[i] = 0，而水平线在高度为2的位置，2 - 0 = 2；
• 为什么水平线高度为2？
  • 取决于 min（往左边找最高的柱子高，往右边找最高的柱子）
  • 即min（max(height[0…i]),max( height[i…end])） - height[i]
    
    
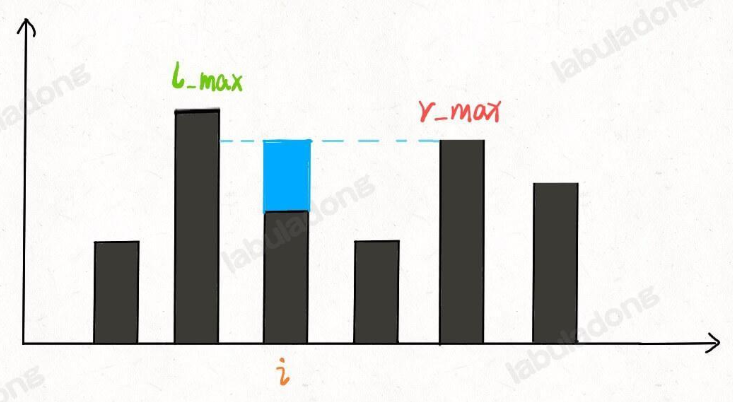
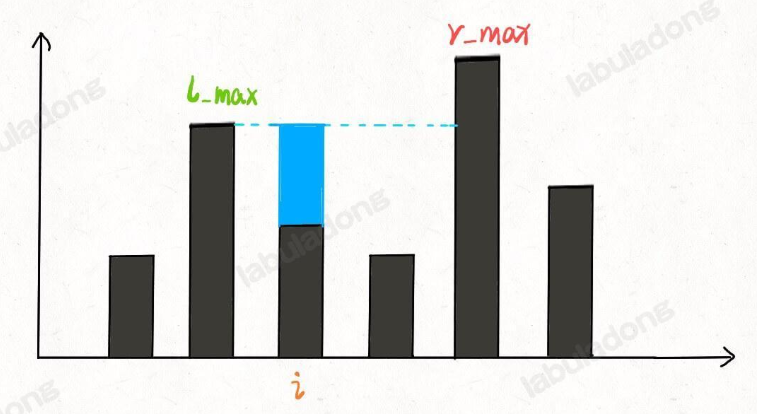
    这就是本题核心思路：

class Solution {
public:int trap(vector<int>& height) {int n = height.size();int res = 0;for (int i = 1; i < n - 1;i++) {int l_max = 0;int r_max = 0;for (int j = i; j >= 0; j--) {// 往左找 l_maxl_max = max(l_max, height[j]);// }for (int j = i;) {r_max = max(r_max, height[j]);}res += min(l_max, r_max) - height[i];}return res;}
};

时间复杂度$O(N^2)$
问题出在，寻找左右两边的r_max 和 l_max 的方式非常笨拙。

注意：寻找左右最高点的时候，出发点是自身，包含自身的！如果自身就是最高，则i左右高点都是自身，后续计算res时减去自身就是0!

解法二：备忘录优化
每个位置 i 都要计算 r_max 和 l_max 吗？我们直接把每个位置需要的r_max 和 l_max结果都提前计算出来，记录下来不就行了！
将解法一中的 r_max 和 l_max 改进为 数组 r_max[i] 和 l_max[i]

• l_max[i] 表示位置 i 左边最高的柱子高度；
• r_max[i] 表示位置 i 右边最高的柱子高度

class Solution {
public:int trap(vector<int>& height) {int n = height.size();int res = 0;// 双备忘录vector<int> l_max(n);	// l_max[i] 表示 i 左边最大的柱子高vector<int> r_max(n);// 初始化备忘录l_max[0] = height[0];r_max[n - 1] = height[n - 1];// 从左向右计算l_maxfor (int i = 1; i < n; i++) {	// i 左侧最高高度，包含 i 自身l_max[i] = std::max(height[i], l_max[i - 1])}// 从右往左计算r_maxfor (int i = n - 2; i >= 0; i--) {r_max[i] = std::max(height[i], r_max[i + 1])}		// 计算答案for (int i = 1; i <= n - 2; i++) {res += std::min(l_max[i], r_max[i]) - height[i];}return res;}
};

其实思路完全就是解法一的暴力，只是避免了重复计算，算是空间换时间，时间复杂度优化到$O(N)$，但是空间复杂度也是$O(N)$。

有什么办法能优化空间复杂度？

解法三：双指针

class Solution {
public:int trap(vector<int>& height) {// 左右指针int n = height.size();int left = 0;int right = n - 1;// 定义int l_max = 0;int r_max = 0;int res = 0;while (left < right) {l_max = max(l_max, height[left]);r_max = max(r_max, height[right]);// res += min(l_max, r_max) - height[i]if (l_max < r_max) {	// 左边低res += } else {  				// 右边高 }}}};