L2正则化:

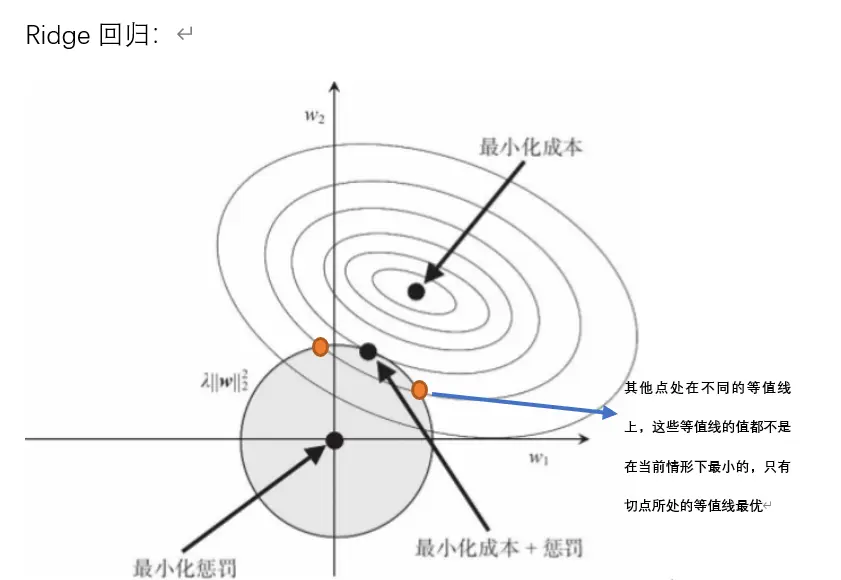
图中用几何方式形象地解释了 Ridge 回归（L2正则化）的原理。

① 阴影圆：可以理解为（w1^2 + w2^2）​≤R^2，圆周表示目标函数的约束线，这个圆表示了我们的参数 (w1,w2)可以活动的范围。

• 为什么要约束？ 因为如果权重太大，模型在训练集上可能表现极好（拟合很好），但在新数据上的表现会大幅下降（过拟合）。
• R 越小意味着什么？圆变小，给权重的空间就越小，惩罚越强，模型更简单，更不容易过拟合。R 越大，模型约等于普通线性回归（无正则化）。

② 最小化成本点（最小二乘估计点）：在图中心的黑点，就是普通线性回归的最小二乘解，也就是“拟合训练数据最好的点”

• 用等高线（椭圆）表现：图里一圈一圈的椭圆，代表对于不同 (w1,w2)参数组合的损失（成本）大小。
  • 离中心越近，损失越小（拟合训练集效果越好）。
  • 离中心越远，损失越大（拟合效果变差）。
• 过拟合的风险：最小化成本点其实对训练集来说是最优解，但往往会过拟合，也就是在新数据上表现很差。所以我们不总是选这个点作为模型的最终解。

我们的目标：不是单纯让损失最小，而是让损失和权重大小都要“

约束下的最优解是什么？

• 如果没有约束，解就在最小化成本点（中心）。
• 有了约束之后，我们只能在圆内找解：我们希望找一个既让损失足够小，又不会让参数过大（也就是不过拟合）。

最终解的位置：

• 这就是图里圆和某个等高线“刚好相切”的那个点，既满足了“损失尽量小”，又不超出圆圈（不让参数过大）。这个点就是 带有L2惩罚的解。

L1正则化:

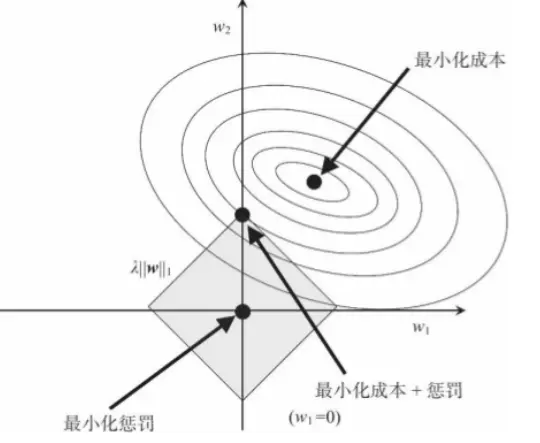
L1, L2 的区别

对于 L2 来说，限定区域是圆，这样，得到的解 w1 或 w2 为 0 的概率很小，很大概率是非零的。

对于 L1 来说，限定区域是正方形，方形的最优解位置通常是在是尖锐点，这从视觉和常识上来看是很容易理解的。也就是说，方形的凸点会更接近最优解对应的 w 位置，而从图中我们可以知道凸点处必有 w1 或 w2 为 0。这样，得到的解 w1 或 w2 为零的概率就很大了。

reference:

以几何思维理解L1&L2正则化 - 简书

(5 封私信) 【通俗易懂】机器学习中 L1 和 L2 正则化的直观解释 - 知乎