线性回归是机器学习中最基础、最核心的算法之一,它为我们理解更复杂的模型奠定了基础。本文将带你全面解析线性回归的方方面面。
1. 什么是回归?
回归分析用于预测连续型数值。它研究自变量(特征)与因变量(目标)之间的关系。例如:
- 根据房屋面积、地段预测房价
- 根据广告投入预测产品销量
核心目标:找到特征与目标之间的最佳映射函数。
2. 线性回归
核心假设:目标变量(y)与特征变量(x)之间存在线性关系。
模型表达式:
y = w0 + w1*x1 + w2*x2 + ... + wn*xn + ε
y:预测目标w0:偏置项(截距)w1..wn:特征权重(斜率)ε:随机误差
3. 损失函数:衡量模型误差
均方误差(MSE) 是最常用损失函数:
MSE = (1/m) * Σ(y_i - ŷ_i)^2
m:样本数量y_i:真实值ŷ_i:预测值
目标:找到一组权重 w,使 MSE 最小化。
数据: [[4.2, 3.8],[4.2, 2.7],[2.7, 2.4],[0.8, 1.0],[3.7, 2.8],[1.7, 0.9],[3.2, 2.9]]
我们假设 这个最优的方程是:
y=wx+by=wx+by=wx+b
这样的直线随着w和b的取值不同 可以画出无数条
在这无数条中,哪一条是比较好的呢?
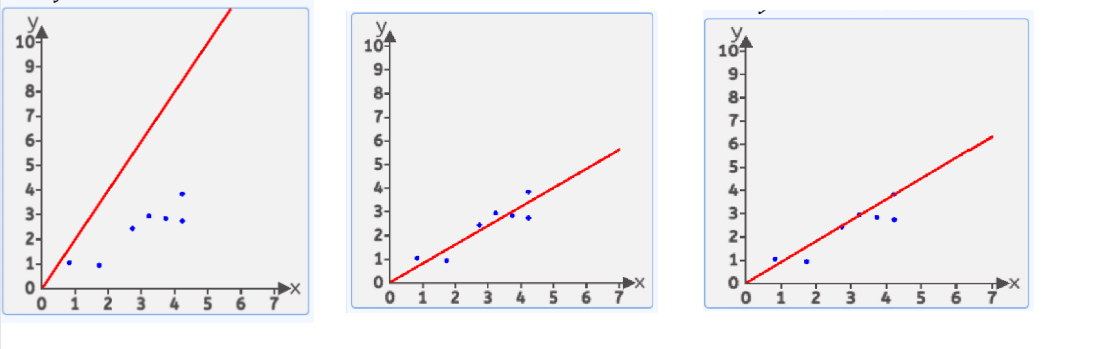
我们有很多方式认为某条直线是最优的,其中一种方式:均方差
就是每个点到线的竖直方向的距离平方 求和 在平均 最小时 这条直接就是最优直线
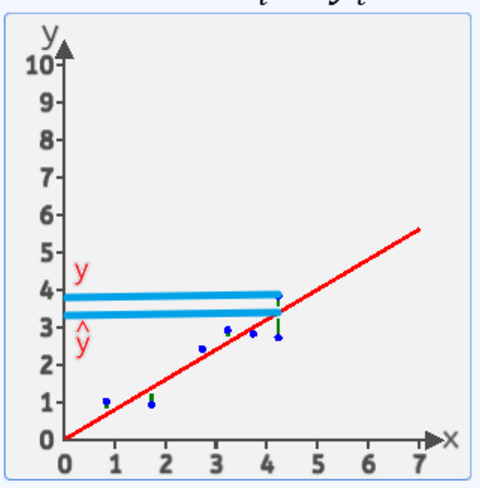
假设: y=wx+by=wx+by=wx+b
把x1,x2,x3...x_1,x_2,x_3...x1,x2,x3...带入进去 然后得出:
y1,=wx1+by_1^,=wx_1+by1,=wx1+b
y2,=wx2+by_2^,=wx_2+by2,=wx2+b
y3,=wx3+by_3^,=wx_3+by3,=wx3+b
…
然后计算y1−y1,{y_1-y_1^,}y1−y1, 表示第一个点的真实值和计算值的差值 ,然后把第二个点,第三个点…最后一个点的差值全部算出来
有的点在上面有点在下面,如果直接相加有负数和正数会抵消,体现不出来总误差,平方后就不会有这个问题了
所以最后:
总误差(也就是传说中的损失):
loss1=(y1−y1,)2+(y2−y2,)2+....(yn−yn,)2{(y_1-y_1^,)^2}+{(y_2-y_2^,)^2}+....{(y_n-y_n^,)^2}(y1−y1,)2+(y2−y2,)2+....(yn−yn,)2
平均误差(总误差会受到样本点的个数的影响,样本点越多,该值就越大,所以我们可以对其平均化,求得平均值,这样就能解决样本点个数不同带来的影响)
这样就得到了传说中的损失函数:
eˉ=1n∑i=1n(yi−wxi−b)2\bar e = \frac{1}{n} \textstyle\sum_{i=1}^{n}(y_{i}-w x_{i} - b)^{2}eˉ=n1∑i=1n(yi−wxi−b)2
总结
1.实际数据中 x和y组成的点 不一定是全部落在一条直线上
2.我们假设有这么一条直线 y=wx+by=wx+by=wx+b 是最符合描述这些点的
3.最符合的条件就是这个方程带入所有x计算出的所有y与真实的y值做 均方差计算
4.找到均方差最小的那个w
5.这样就求出了最优解的函数(前提条件是假设b=0)
4. 多参数回归
当特征数量 > 1 时,使用矩阵运算更高效:
ŷ = X · w
X:m×(n+1) 维特征矩阵(含偏置列)w:(n+1)×1 维权重向量
上面案例中,实际情况下,影响这种植物高度的不仅仅有温度,还有海拔,湿度,光照等等因素:
实际情况下,往往影响结果y的因素不止1个,这时x就从一个变成了n个,x1,x2,x3...xnx_1,x_2,x_3...x_nx1,x2,x3...xn 上面的思路是对的,但是求解的公式就不再适用了
案例: 假设一个人健康程度怎么样,由很多因素组成
| 被爱 | 学习指数 | 抗压指数 | 运动指数 | 饮食情况 | 金钱 | 心态 | 压力 | 健康程度 |
|---|---|---|---|---|---|---|---|---|
| 0 | 14 | 8 | 0 | 5 | -2 | 9 | -3 | 339 |
| -4 | 10 | 6 | 4 | -14 | -2 | -14 | 8 | -114 |
| -1 | -6 | 5 | -12 | 3 | -3 | 2 | -2 | 30 |
| 5 | -2 | 3 | 10 | 5 | 11 | 4 | -8 | 126 |
| -15 | -15 | -8 | -15 | 7 | -4 | -12 | 2 | -395 |
| 11 | -10 | -2 | 4 | 3 | -9 | -6 | 7 | -87 |
| -14 | 0 | 4 | -3 | 5 | 10 | 13 | 7 | 422 |
| -3 | -7 | -2 | -8 | 0 | -6 | -5 | -9 | -309 |
| 11 | 14 | 8 | 10 | 5 | 10 | 8 | 1 | ? |
求如果karen的各项指标是:
被爱:11 学习指数:14 抗压指数:8 运动指数:10 饮食水平:5 金钱:10 心态:8 压力:1
那么karen的健康程度是多少?
直接能想到的就是八元一次方程求解:
14w2+8w3+5w5+−2w6+9w7+−3w8=39914w_2+8w_3+5w_5+-2w_6+9w_7+-3w_8=39914w2+8w3+5w5+−2w6+9w7+−3w8=399
−4w1+10w2+6w3+4w4+−14w5+−2w6+−14w7+8w8=−144-4w_1+10w_2+6w_3+4w_4+-14w_5+-2w_6+-14w_7+8w_8=-144−4w1+10w2+6w3+4w4+−14w5+−2w6+−14w7+8w8=−144
−1w1+−6w2+5w3+−12w4+3w3+−3w6+2w7+−2w8=30-1w_1+-6w_2+5w_3+-12w_4+3w_3+-3w_6+2w_7+-2w_8=30−1w1+−6w2+5w3+−12w4+3w3+−3w6+2w7+−2w8=30
5w1+−2w2+3w3+10w4+5w5+11w6+4w7+−8w8=1265w_1+-2w_2+3w_3+10w_4+5w_5+11w_6+4w_7+-8w_8=1265w1+−2w2+3w3+10w4+5w5+11w6+4w7+−8w8=126
−15w1+−15w2+−8w3+−15w4+7w5+−4w6+−12w7+2w8=126-15w_1+-15w_2+-8w_3+-15w_4+7w_5+-4w_6+-12w_7+2w_8=126−15w1+−15w2+−8w3+−15w4+7w5+−4w6+−12w7+2w8=126
11w1+−10w2+−2w3+4w4+3w5+−9w6+−6w7+7w8=−8711w_1+-10w_2+-2w_3+4w_4+3w_5+-9w_6+-6w_7+7w_8=-8711w1+−10w2+−2w3+4w4+3w5+−9w6+−6w7+7w8=−87
−14w1+4w3+−3w4+5w5+10w6+13w7+7w8=422-14w_1+4w_3+-3w_4+5w_5+10w_6+13w_7+7w_8=422−14w1+4w3+−3w4+5w5+10w6+13w7+7w8=422
−3w1+−7w2+−2w3+−8w4+−6w6+−5w7+−9w8=−309-3w_1+-7w_2+-2w_3+-8w_4+-6w_6+-5w_7+-9w_8=-309−3w1+−7w2+−2w3+−8w4+−6w6+−5w7+−9w8=−309
解出 权重 w(w1,w2...w8)w(w_1,w_2...w_8)w(w1,w2...w8) 然后带入即可求出karen的健康程度
权重即重要程度,某一项的权重越大说明它影响最终健康的程度越大
但是这有一个前提:这个八元一次方程组得有解才行
因此我们还是按照损失最小的思路来求权重 w(w1,w2...w8)w(w_1,w_2...w_8)w(w1,w2...w8)
多元线性回归:
y,=w1x1+w2x2+....wnxn+by^,=w_1x_1+w_2x_2+....w_nx_n+by,=w1x1+w2x2+....wnxn+b
b是截距,我们也可以使用w0w_0w0来表示只要是个常量就行
y,=w1x1+w2x2+....wnxn+w0y^,=w_1x_1+w_2x_2+....w_nx_n+w_0y,=w1x1+w2x2+....wnxn+w0
y,=w1x1+w2x2+....wnxn+w0∗1y^,=w_1x_1+w_2x_2+....w_nx_n+w_0*1y,=w1x1+w2x2+....wnxn+w0∗1
那么损失函数就是
loss=[(y1−y1,)2+(y2−y2,)2+....(yn−yn,)2]/nloss=[(y_1-y_1^,)^2+(y_2-y_2^,)^2+....(y_n-y_n^,)^2]/nloss=[(y1−y1,)2+(y2−y2,)2+....(yn−yn,)2]/n
如何求得对应的W(w1,w2..w0)W{(w_1,w_2..w_0)}W(w1,w2..w0) 使得loss最小呢?
数学家高斯给出了答案,就是最小二乘法。
5. 最小二乘法(OLS)
h(x)=w1x1+w2x2+w3x3+w4x4+w5x5+w6x6+w7x7+w8x8+w0x0h(x)=w_1x_1+w_2x_2+w_3x_3+w_4x_4+w_5x_5+w_6x_6+w_7x_7+w_8x_8+w_0x_0h(x)=w1x1+w2x2+w3x3+w4x4+w5x5+w6x6+w7x7+w8x8+w0x0
loss=[(h1(x)−y1)2+(h2(x)−y2)2+...(hn(x)−yn)2]/n=1n∑i=1n(h(xi)−yi)2=1n∣∣(XW−y)∣∣2=12∣∣(XW−y)∣∣2这就是传说中的最小二乘法公式∣∣A∣∣2是欧几里得范数的平方 也就是每个元素的平方相加loss=[(h_1(x)-y_1)^2+(h_2(x)-y_2)^2+...(h_n(x)-y_n)^2]/n\\=\frac{1}{n} \textstyle\sum_{i=1}^{n}(h(x_{i})-y_{i})^{2}\\=\frac{1}{n}||(XW-y)||^2\\=\frac{1}{2}||(XW-y)||^2 这就是传说中的最小二乘法公式 \\ ||A||^2 是欧几里得范数的平方\,也就是每个元素的平方相加loss=[(h1(x)−y1)2+(h2(x)−y2)2+...(hn(x)−yn)2]/n=n1∑i=1n(h(xi)−yi)2=n1∣∣(XW−y)∣∣2=21∣∣(XW−y)∣∣2这就是传说中的最小二乘法公式∣∣A∣∣2是欧几里得范数的平方也就是每个元素的平方相加
但求得最合适的w还需对其求导,这里使用链式求导,(推荐,因为后期深度学习全是这种):
内部函数是f(W)=XW−yf(W) = XW - yf(W)=XW−y,外部函数是 g(u)=12u2g(u) = \frac{1}{2} u^2g(u)=21u2,其中 u=f(W)u = f(W)u=f(W)。
外部函数的导数:∂g∂u=u=XW−y\frac{\partial g}{\partial u} = u = XW - y∂u∂g=u=XW−y
内部函数的导数:∂f∂W=XT\frac{\partial f}{\partial W} = X^T∂W∂f=XT
应用链式法则,我们得到最终的梯度:∂L∂W=(∂g∂u)(∂f∂W)=(XW−y)XT\frac{\partial L}{\partial W} = \left( \frac{\partial g}{\partial u} \right) \left( \frac{\partial f}{\partial W} \right) = (XW - y) X^T∂W∂L=(∂u∂g)(∂W∂f)=(XW−y)XT
有了W,回到最初的问题:
求如果karen的各项指标是:
被爱:11 学习指数:14 抗压指数:8 运动指数:10 饮食水平:5 金钱:10 权利:8 压力:1
那么karen的健康程度是多少?
分别用W各项乘以新的X 就可以得到y健康程度
5.1 矩阵公式关键
- 权重解:W=(XTX)−1XTyW=(X^TX)^{-1}X^TyW=(XTX)−1XTy
- 需确保 XTXX^T XXTX 可逆(否则需正则化)
5.3 Scikit-Learn 实现
from sklearn.linear_model import LinearRegressionmodel = LinearRegression()
model.fit(X_train, y_train) # 训练模型
y_pred = model.predict(X_test) # 预测
5.4 示例代码(含可视化)
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LinearRegression# 生成数据
X = np.array([[1], [2], [3]])
y = np.array([2, 4, 5])# 训练模型
model = LinearRegression()
model.fit(X, y)# 可视化
plt.scatter(X, y, color='blue')
plt.plot(X, model.predict(X), color='red')
plt.title('Linear Regression Fit')
plt.show()
6. 梯度下降(GD):迭代优化法
当特征维度高、数据量大时,最小二乘法计算成本过高,梯度下降成为更优选择。
6.1 核心概念
通过迭代调整权重,逐步逼近损失函数最小值。
形象比喻:在山顶蒙眼下山,每步沿最陡峭方向前进。
6.2 梯度下降步骤
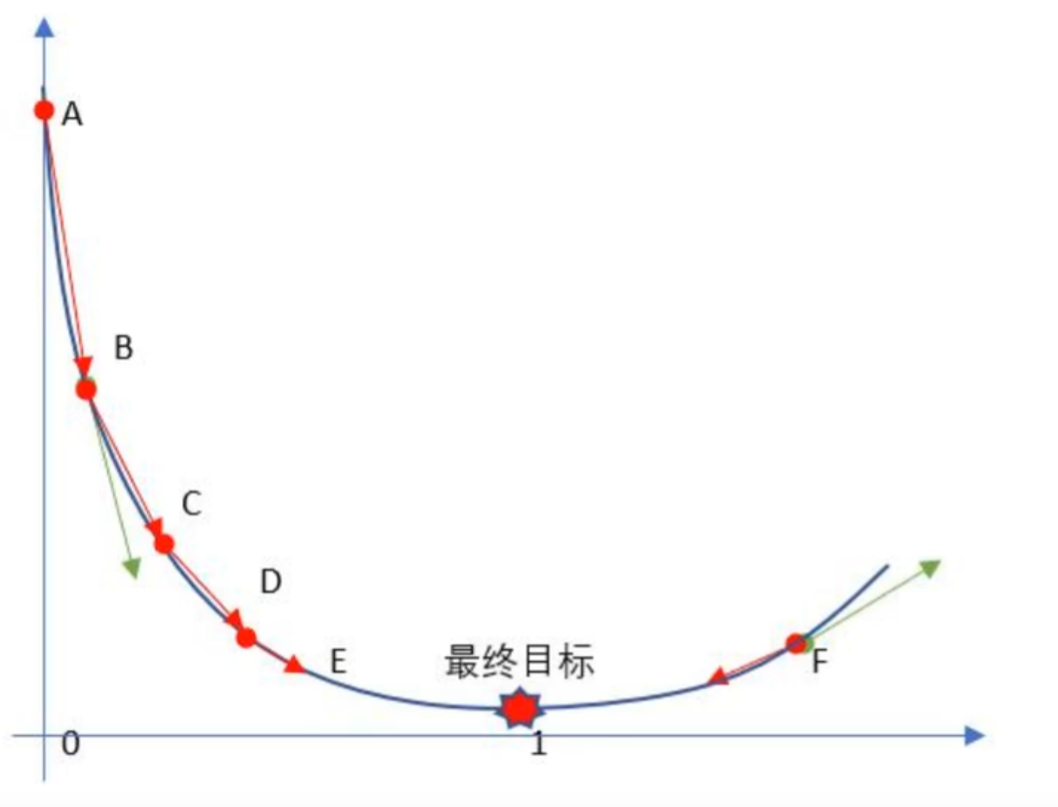
梯度下降流程就是“猜"正确答案的过程:
1、Random随机数生成初始W,随机生成一组成正太分布的数值w0,w1,w2....wnw_0,w_1,w_2....w_nw0,w1,w2....wn,这个随机是成正太分布的(高斯说的)
2、求梯度g,梯度代表曲线某点上的切线的斜率,沿着切线往下就相当于沿着坡度最陡峭的方向下降.
3、if g < 0,w变大,if g >0,w变小(目标左边是斜率为负右边为正 )
4、判断是否收敛,如果收敛跳出迭代,如果没有达到收敛,回第2步再次执行2~4步收敛的判断标准是:随着迭代进行查看损失函数Loss的值,变化非常微小甚至不再改变,即认为达到收敛
5.上面第4步也可以固定迭代次数
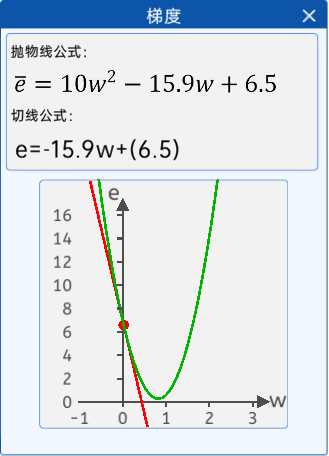
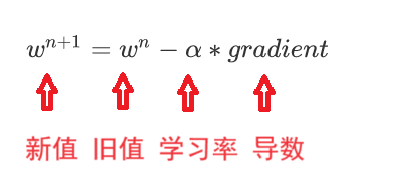
随机给一个w初始值,然后就不停的修改它,直到达到抛物线最下面附近,比如
w=0.2
w=w-0.01*w为0.2时的梯度(导数) 假设算出来是 0.24
w=w-0.01*w为0.24时的梯度(导数) 假设算出来是 0.33
w=w-0.01*w为0.33时的梯度(导数) 假设算出来是 0.51
w=w-0.01*w为0.51时的梯度(导数) 假设算出来是 0.56
w=w-0.01*w为0.56时的梯度(导数) 假设算出来是 0.58
w=w-0.01*w为0.58时的梯度(导数) 假设算出来是 0.62
就这样一直更新下去,会在真实值附近,我们可以控制更新的次数
关于随机的w在左边和右边问题:
因为导数有正负
如果在左边 导数是负数 减去负数就是加 往右移动
如果在右边 导数是正数 减去正数就是减 往左移动
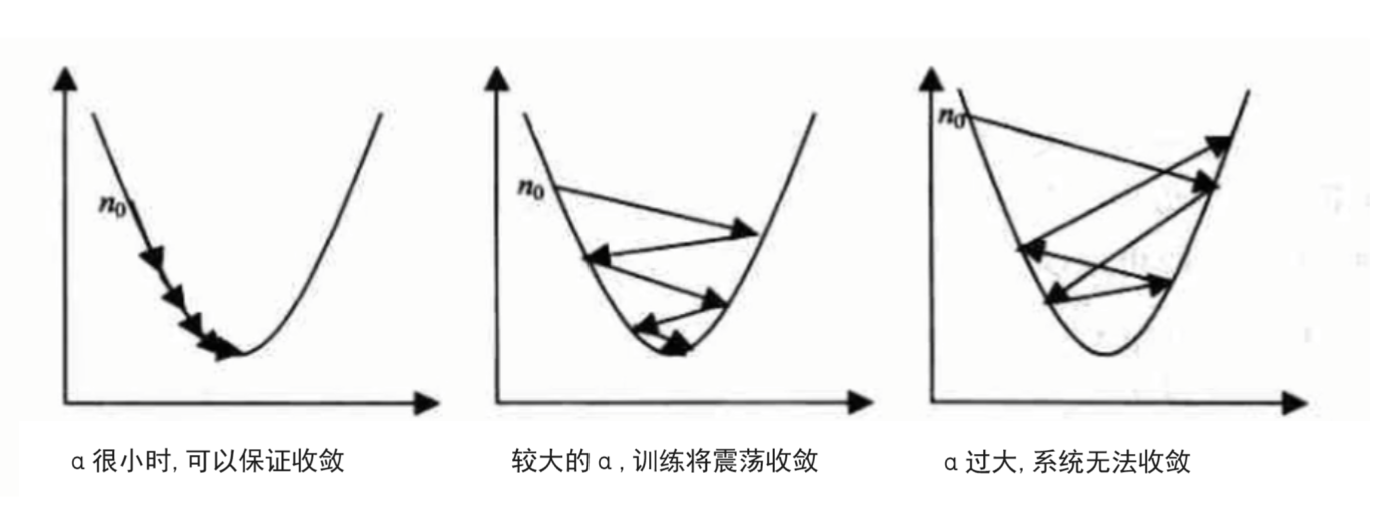
6.3 学习率(α)的重要性
- α 过大:跳过最优解,无法收敛
- α 过小:收敛速度极慢
- 实践建议:尝试 0.001、0.01、0.1 等值
6.4 手写梯度下降实现
我们自己用代码亲自实现一遍梯度下降,之后使用API时就明白它底层的核心实现过程了.
1.假设损失函数是只有一个w1w_1w1特征的抛物线:
loss(w1)=(w1−3.5)2−4.5w1+10loss(w_1)=(w_1-3.5)^2-4.5w_1+10loss(w1)=(w1−3.5)2−4.5w1+10
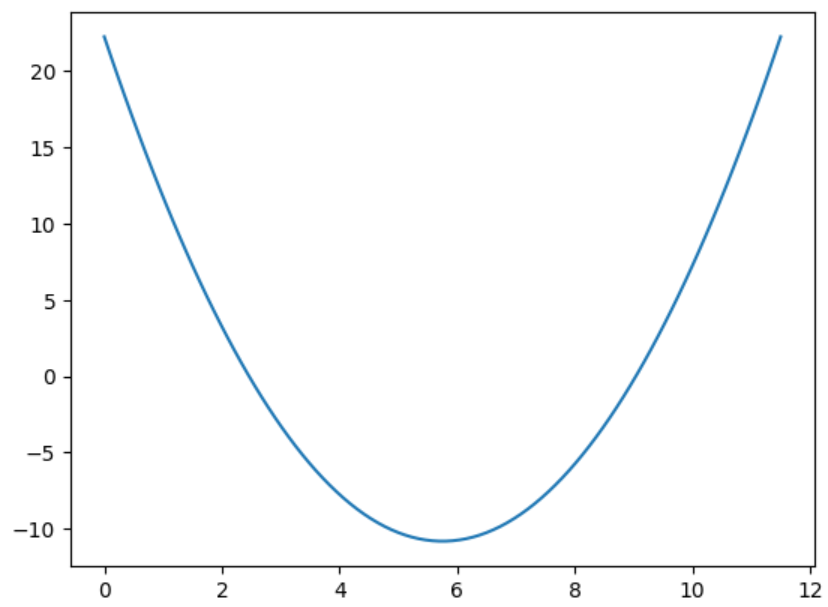
我们要求解这个抛物线最小值时的横坐标w1w_1w1的值
#1.列损失函数 画出函数图像
loss=lambda w_1:(w_1-3.5)**2-4.5*w_1+10
w_1=np.linspace(0,11.5,100)
plt.plot(w_1,loss(w_1))
#2.求这个损失函数的最小值:梯度下降
def cb():g=lambda w_1:2*(w_1-3.5)-4.5#导函数t0,t1=1,100 alpha=t0/t1#学习率,设置大和过大会导致震荡或者无法收敛w_1=np.random.randint(0,10,size=1)[0]#随机初始值#控制更新次数for i in range(1000):alpha=t0/(i+t1)#控制学习率 逐步变小w_1=w_1-alpha*g(w_1)#梯度下降公式print("更新后的w_1:",w_1)
cb()
6.5 Scikit-Learn 实现
官方的梯度下降API常用有三种:
批量梯度下降BGD(Batch Gradient Descent)
小批量梯度下降MBGD(Mini-BatchGradient Descent)
随机梯度下降SGD(Stochastic Gradient Descent)。
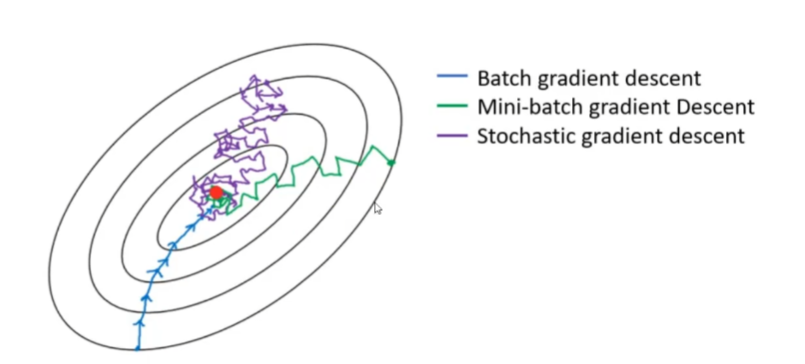
三种梯度下降有什么不同呢?
- Batch Gradient Descent (BGD): 在这种情况下,每一次迭代都会使用全部的训练样本计算梯度来更新权重。这意味着每一步梯度更新都是基于整个数据集的平均梯度。这种方法的优点是每次更新的方向是最准确的,但缺点是计算量大且速度慢,尤其是在大数据集上。
- Mini-Batch Gradient Descent (MBGD): 这种方法介于批量梯度下降和随机梯度下降之间。它不是用全部样本也不是只用一个样本,而是每次迭代从数据集中随机抽取一小部分样本(例如,从500个样本中选取32个),然后基于这一小批样本的平均梯度来更新权重。这种方法在准确性和计算效率之间取得了一个平衡。
- Stochastic Gradient Descent (SGD): 在随机梯度下降中,每次迭代仅使用随机单个样本(或有时称为“例子”)来计算梯度并更新权重。这种方法能够更快地收敛,但由于每次更新都基于单个样本,所以会导致权重更新路径不稳定。
from sklearn.linear_model import SGDRegressormodel = SGDRegressor(learning_rate='constant', eta0=0.01)
model.fit(X_train, y_train)
梯度下降变体对比
| 类型 | 批量大小 | 速度 | 稳定性 | 适用场景 |
|---|---|---|---|---|
| BGD | 全批量(m) | 慢 | 高 | 小数据集 |
| SGD | 单样本(1) | 快 | 低(震荡) | 大规模在线学习 |
| MBGD | 小批量(b) | 中 | 中 | 最常用(b=32/64) |
6.9 梯度下降优化技巧
-
动量(Momentum):
v = β*v + (1-β)*gradient
w = w - α*v
加速收敛,减少震荡 -
自适应学习率:
- AdaGrad:为每个参数调整 α
- RMSProp:解决 AdaGrad 学习率衰减问题
- Adam(最常用):结合 Momentum 和 RMSProp
-
标准化:前期数据的预处理
正则化:防止过拟合
关键总结
- 回归预测连续值,线性回归假设线性关系
- MSE是常用损失函数,通过最小化MSE求解模型
- 最小二乘法求解析解,梯度下降求数值解
- 学习率是梯度下降的核心超参数
- MBGD在实践中最常用,Adam是最流行的优化器
理解线性回归不仅能解决实际问题,更是学习深度学习、支持向量机等复杂模型的基石。掌握其数学本质和实现细节,才能在机器学习道路上走得更远。

 的开源库详解)






检测头结构创新,实现有效涨点)


AXI协议总线学习)


![[特殊字符]️ 整个键盘控制无人机系统框架](http://pic.xiahunao.cn/[特殊字符]️ 整个键盘控制无人机系统框架)
LogisticRegression)


)
:CountDownLatch 与 Semaphore 的协作应用)