数据结构----栈和队列认识

目录

栈（后进先出）

栈的实现

头文件

初始化

入栈

注意：

bool 判空

出栈----栈顶

注意

出栈顶元素，元素不会删除

注意：

获取栈中有效个数

销毁栈

源文件操作

用栈实现递归*

队列（先进先出）

队列实现

头文件（基本操作）：

结构

初始化

判空

入队----队尾

出队----队头

优势：

取队头队尾数据

优势：

销毁

栈（后进先出）

是⼀种特殊的线性表，其只允许在固定的⼀端进⾏插⼊和删除元素操作。进⾏数据插⼊和删除操作
的⼀端称为栈顶，另⼀端称为栈底。
压栈：栈的插⼊操作叫做进栈/压栈/⼊栈，入数据在栈顶。
出栈：栈的删除操作叫做出栈。出数据也在栈顶。

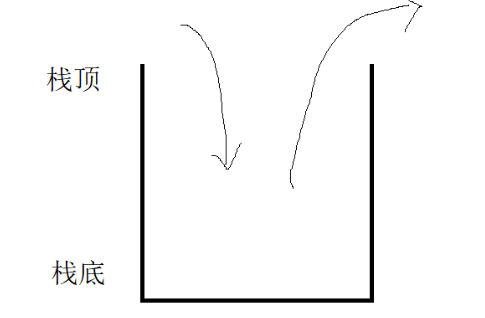
底层结构是由数组实现的，相对来说数组在尾结点插入快

逻辑结构和物理结构都是线性的

栈的实现

头文件

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
//定义栈的结构
typedef int STDataType;
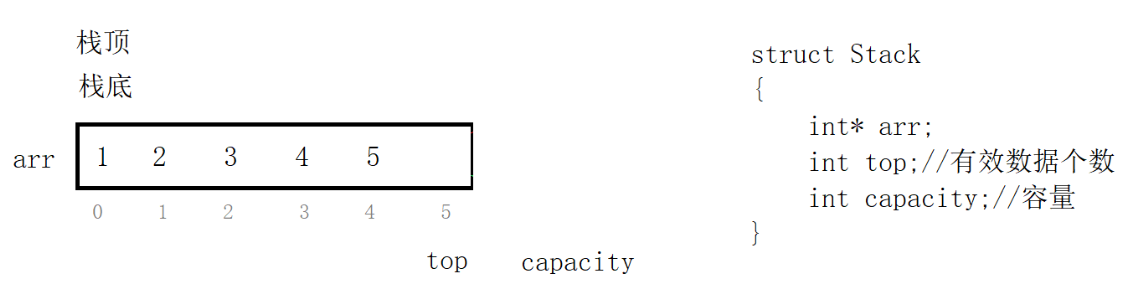
typedef struct Stack
{STDataType* arr;int top;//有效数据个数int capacity;//容量
}ST;//初始化
void StackInit(ST* ps);//栈是否为空
bool STEmpty(ST* ps);//入栈----栈顶
void StackPush(ST* ps, STDataType x);//出栈----栈顶
void StackPop(ST* ps);//出栈顶数据
STDataType StackTop(ST* ps);
\ No newline at end of file
STDataType StackTop(ST* ps);//获取栈中有效元素个数
int StackSize(ST* ps);//栈是否为空
bool STEmpty(ST* ps);

初始化

//初始化
void StackInit(ST* ps)
{assert(ps);ps->arr = NULL;ps->top = ps->capacity = 0;
}

使用前先调用StackInit初始化栈，然后才能进行入栈等其他操作，否则可能会导致未定义行为。

入栈

//入栈----栈顶
void StackPush(ST* ps, STDataType x)
{if (ps->top == ps->capacity){//增容int newCapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;STDataType* tmp = (STDataType*)realloc(ps->arr, newCapacity * sizeof(STDataType));if (tmp == NULL){perror("realloc");exit(1);}//空间申请成功ps->arr = tmp;ps->capacity = newCapacity;}ps->arr[ps->top++] = x;
}
  1. 首先检查栈是否已满（ps->top == ps->capacity）
  2. 如果栈满，则进行扩容操作：
    • 初始容量为 0 时，扩容到 4 个元素
    • 否则，按照 2 倍容量进行扩容
    • 使用realloc重新分配内存空间
    • 处理内存分配失败的情况（打印错误并退出程序）
  3. 将新元素x放入栈顶位置（ps->arr[ps->top]）
  4. 栈顶指针top自增，指向新的栈顶位置

注意：

  • ps指针不为空,一般断言一下。
  • 栈结构ST已经正确初始化
  • STDataType已经定义（通常是某种基本数据类型）

bool 判空

//栈是否为空
bool STEmpty(ST* ps)
{assert(ps);return ps->top == 0;
}

为空则返回true,非空则是false

出栈----栈顶

//出栈----栈顶
void StackPop(ST* ps)
{assert(!STEmpty(ps));--ps->top;
}
  • 效率高，时间复杂度为 O (1)
  • 实现简洁，通过移动栈顶指针而非真正释放内存来 "删除" 元素

注意

  • 该函数依赖STEmpty函数来判断栈是否为空，需要确保STEmpty已正确实现
  • 出栈操作只是逻辑上移除元素（移动栈顶指针），并未真正释放内存，这是栈实现的常见做法
  • 调用前应确保栈不为空，否则assert会触发程序中断

出栈顶元素，元素不会删除


//出栈顶数据,元素不会删除
STDataType StackTop(ST* ps)
{assert(!STEmpty(ps));return ps->arr[ps->top - 1];}

注意：

  • 栈顶指针top指向的是下一个可以插入元素的位置，所以当前栈顶元素的索引是top - 1
  • 仅仅返回元素值，不修改top指针，因此元素不会被 "删除"
  • 依赖STEmpty函数判断栈是否为空，需要确保该函数已正确实现

获取栈中有效个数

//获取栈中有效元素个数
int StackSize(ST* ps)
{return ps->top;
}
  1. 直接返回栈顶指针top的值作为栈中有效元素的个数
  2. 这是因为栈的实现中top指针恰好表示了下一个可以插入元素的位置，同时也等于当前栈中元素的数量
  3. 时间复杂度为 O (1)，效率极高

销毁栈

void StackDestroy(ST* ps)
{assert(ps);free(ps->arr);  // 释放底层数组内存ps->arr = NULL; // 避免野指针ps->top = ps->capacity = 0; // 重置状态
}

源文件操作

#include"Stack.h"
void test1()
{ST st;StackInit(&st);StackPush(&st,1);StackPush(&st, 1);StackPush(&st, 2);StackPush(&st, 3);StackPush(&st,4);StackPush(&st, 4);StackPush(&st, 5);/*StackPop(&st);StackPop(&st);StackPop(&st);StackPop(&st);StackPop(&st);StackPop(&st);StackPop(&st);*//*while (!STEmpty(&st)){int top = StackTop(&st);printf("%d ", top);StackPop(&st);}*/int size = StackSize(&st);printf("%d\n", size);
}
int main()
{test1();return 0;
}

用栈实现递归*

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>// 定义栈结构
typedef int STDataType;
typedef struct Stack {STDataType* arr;int top;        // 栈顶指针，指向栈顶元素的下一个位置int capacity;   // 容量
} ST;// 栈的基本操作
void StackInit(ST* ps) {assert(ps);ps->arr = NULL;ps->top = ps->capacity = 0;
}void StackPush(ST* ps, STDataType x) {assert(ps);if (ps->top == ps->capacity) {int newCapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;STDataType* tmp = (STDataType*)realloc(ps->arr, newCapacity * sizeof(STDataType));if (tmp == NULL) {perror("realloc");exit(1);}ps->arr = tmp;ps->capacity = newCapacity;}ps->arr[ps->top++] = x;
}void StackPop(ST* ps) {assert(ps);assert(ps->top > 0);ps->top--;
}STDataType StackTop(ST* ps) {assert(ps);assert(ps->top > 0);return ps->arr[ps->top - 1];
}int StackSize(ST* ps) {assert(ps);return ps->top;
}void StackDestroy(ST* ps) {assert(ps);free(ps->arr);ps->arr = NULL;ps->top = ps->capacity = 0;
}// 用栈模拟递归计算n的阶乘
int Factorial(int n) {if (n < 0) return -1; // 处理异常情况ST stack;StackInit(&stack);// 1. 模拟递归调用过程：将所有需要计算的数值入栈while (n > 1) {StackPush(&stack, n);n--;}// 2. 模拟递归返回过程：从栈顶开始计算int result = 1;while (StackSize(&stack) > 0) {result *= StackTop(&stack);StackPop(&stack);}StackDestroy(&stack);return result;
}int main() {int num = 5;int result = Factorial(num);printf("%d的阶乘是: %d\n", num, result); // 输出：5的阶乘是: 120return 0;
}

队列（先进先出）

只允许在⼀端进⾏插⼊数据操作，在另⼀端进⾏删除数据操作的特殊线性表
⼊队列：进⾏插⼊操作的⼀端称为队尾
出队列：进⾏删除操作的⼀端称为队头

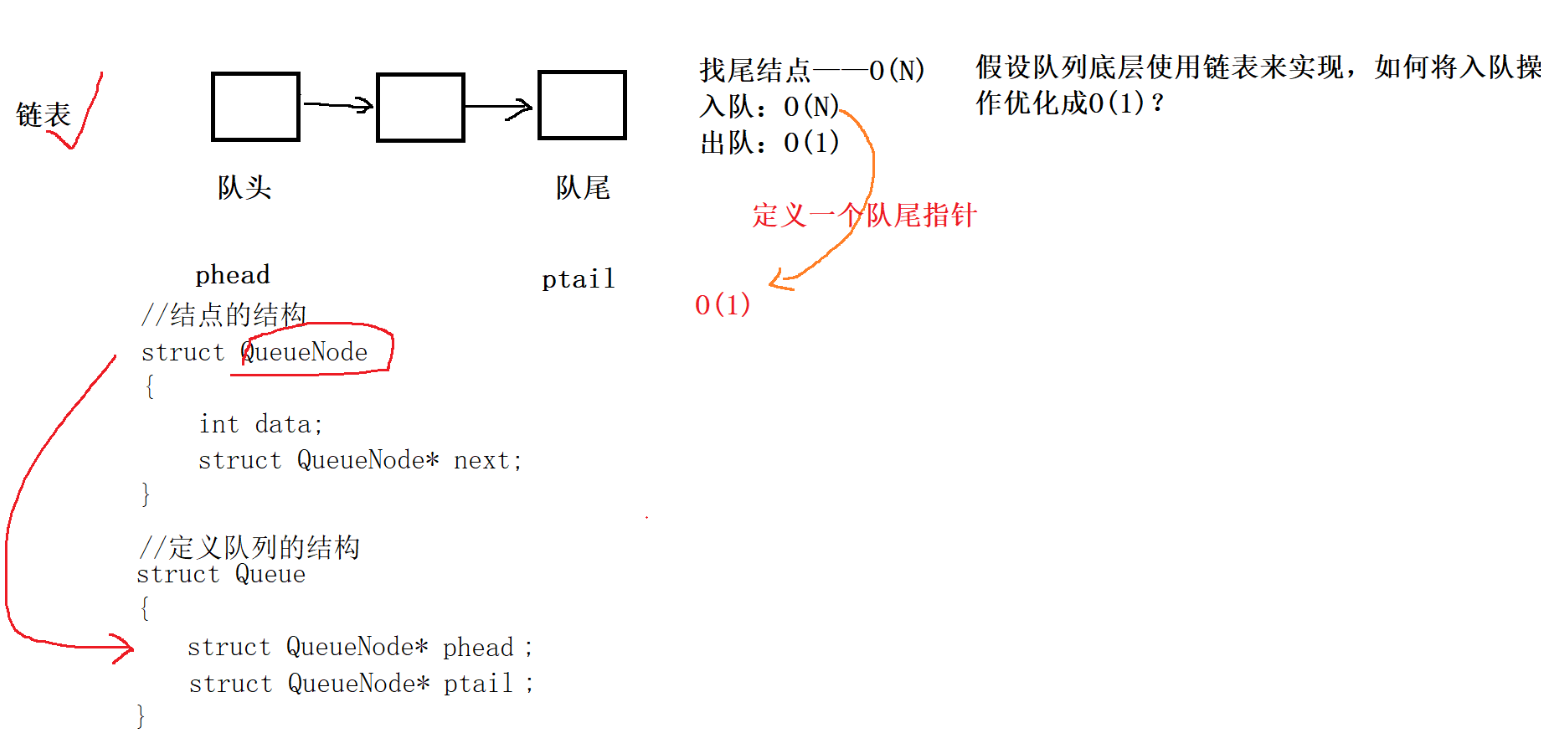
队列实现

头文件（基本操作）：

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
typedef int QDataType;
//队列结点的结构
typedef struct QueueNode
{QDataType data;struct QueueNode* next;
}QueueNode;
//队列的结构
typedef struct Queue
{QueueNode* phead;QueueNode* ptail;//int size; //队列中有效数据个数
}Queue;//初始化
void QueueInit(Queue* pq);
//销毁队列
void QueueDestroy(Queue* pq);//入队——队尾
void QueuePush(Queue* pq, QDataType x);//出队——队头
void QueuePop(Queue* pq);
//队列判空
bool QueueEmpty(Queue* pq);
//队列有效元素个数
int QueueSize(Queue* pq);//取队头数据
QDataType QueueFront(Queue* pq);
//取队尾数据
QDataType QueueBack(Queue* pq);

结构

//队列结点的结构
typedef struct QueueNode
{QDataType data;struct QueueNode* next;
}QueueNode;
//队列的结构
typedef struct Queue
{QueueNode* phead;QueueNode* ptail;//int size; //队列中有效数据个数
}Queue;
  • 插入和删除操作效率高（队尾插入、队首删除均可在 O (1) 时间完成）
  • 不需要预先分配固定大小的内存，动态性好

初始化

//初始化
void QueueInit(Queue* pq)
{assert(pq);pq->phead = pq->ptail = NULL;//pq->size = 0;
}
  1. 使用assert(pq)确保传入的队列指针pq不为空，避免空指针操作
  2. 将队头指针phead和队尾指针ptail都初始化为NULL，表示初始状态下队列为空
  3. 注释掉的pq->size = 0用于初始化队列元素个数（如果保留size成员的话）

判空

/队列判空
bool QueueEmpty(Queue* pq)
{assert(pq);return pq->phead == NULL;
}

入队----队尾

//入队——队尾
void QueuePush(Queue* pq, QDataType x)
{assert(pq);QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));if (newnode == NULL){perror("malloc fail");exit(1);}newnode->data = x;newnode->next = NULL;if (pq ->phead!= NULL)//队列非空{pq->ptail->next = newnode;pq->ptail = newnode;}else//队列为空{pq->phead = pq->ptail = newnode;}//size++;
}
  1. 当队列为空时（phead为NULL），新节点既是队头也是队尾
  2. 当队列非空时，将新节点链接到当前队尾节点（ptail）的next，然后更新ptail指向新节点

出队----队头

//出队——队头
void QueuePop(Queue* pq)
{assert(!QueueEmpty(pq));if (pq->phead == pq->ptail)//只有一个节点，头尾都置为空{free(pq->phead);pq->phead=pq->ptail = NULL;}else{QueueNode* next = pq->phead->next;free(pq->phead);pq->phead = next;}
}
  1. 分两种情况处理：
    • 当队列中只有一个节点时（pq->phead == pq->ptail）：
      • 释放该节点内存
      • 将phead和ptail都置为NULL，保持空队列状态
    • 当队列中有多个节点时：
      • 先保存头节点的下一个节点指针
      • 释放头节点内存
      • 更新phead指向保存的下一个节点

优势：

  • 正确维护了队列的头指针和尾指针状态
  • 避免了内存泄漏（释放了被移除节点的内存）
  • 处理了队列从有元素变为空的边界情况

若包含size,size--保持数量一致

取队头队尾数据

//取队头数据
QDataType QueueFront(Queue* pq)
{assert(!QueueEmpty(pq));return pq->phead->data;
}//取队尾数据
QDataType QueueBack(Queue* pq)
{assert(!QueueEmpty(pq));return pq->ptail->data;}

优势：

  • 时间复杂度都是 O (1)，效率很高
  • 仅获取元素值，不会修改队列的结构和状态
  • 依赖QueueEmpty函数判断队列是否为空，保持了代码的一致性
  • 符合队列 "先进先出" 的特性，分别提供了访问两端元素的接口

销毁

//销毁队列
void QueueDestroy(Queue* pq)
{assert（pq);QueueNode* pcur = pq->phead;while (pcur){QueueNode* next = pcur->next;free(pcur);pcur = next;}pq->phead = pq->ptail =NULL;//pq->size =0;
}

销毁队列是一个通用操作，即使队列为空（初始状态或已清空），也应该允许调用QueueDestroy，这样可以避免在调用销毁函数前还需要手动判断队列是否为空。

允许对空队列进行销毁

  • 当队列为空时，pcur初始为NULL，循环不会执行，直接重置phead和ptail
  • 当队列非空时，循环释放所有节点，最后重置指针

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
如若转载，请注明出处：http://www.pswp.cn/bicheng/92471.shtml
繁体地址，请注明出处：http://hk.pswp.cn/bicheng/92471.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

【Kafka系列】第二篇｜ Kafka 的核心概念、架构设计、底层原理

【Kafka系列】第二篇｜ Kafka 的核心概念、架构设计、底层原理

在大数据和分布式系统飞速发展的今天&#xff0c;消息队列作为高效的通信工具&#xff0c;在系统解耦、异步通信、流量削峰等方面作用显著。 而 Kafka 这款高性能、高吞吐量的分布式消息队列&#xff0c;在日志收集、数据传输、实时计算等场景中应用广泛。 接下来&#xff0c;我…
阅读更多...
Kafka-exporter采集参数调整方案

Kafka-exporter采集参数调整方案

#作者&#xff1a;张桐瑞 文章目录1 问题概述2 修改方案2.1修改参数2.2配置示例3 消费者组均分脚本3.1使用说明3.2脚本内容3.3实现原理说明4 KAFKA-EXPORTER流程代码4.1KAFKA-EXPORTER拉取数据流程1 问题概述 由于kafka-exporter获取kafka指标时间过长&#xff0c;无法通过cur…
阅读更多...
AT32的freertos下modbus TCP移植

AT32的freertos下modbus TCP移植

1.准备模板 打开雅特力官网&#xff0c;也就是带有LwIP的示例。 下载官方源码&#xff1a;modbus 2.移植 我这里是在这里新建两个文件夹&#xff0c;分别是modbus与port&#xff0c;这个任意&#xff0c;只需要将必要的文件加入项目即可。 将源码中的modbus这些都移植过来&a…
阅读更多...
Redis面试精讲 Day 16：Redis性能监控与分析工具

Redis面试精讲 Day 16：Redis性能监控与分析工具

【Redis面试精讲 Day 16】Redis性能监控与分析工具 开篇 欢迎来到"Redis面试精讲"系列第16天&#xff0c;今天我们将深入探讨Redis性能监控与分析工具。在大型分布式系统中&#xff0c;Redis作为关键的数据存储和缓存组件&#xff0c;其性能指标直接影响整个系统的…
阅读更多...
vue3+vue-flow制作简单可拖拽可增删改流程图

vue3+vue-flow制作简单可拖拽可增删改流程图

实现效果实现代码 准备工作 安装依赖 npm install vue-flow/core npm install vue-flow/minimap //小地图 npm install vue-flow/controls //自带的缩放、居中、加锁功能我这里只用到上述三个&#xff0c;还有其余的可根据实际情况配合官方文档使用。 npm install vue-flow/bac…
阅读更多...
itextPdf获取pdf文件宽高不准确

itextPdf获取pdf文件宽高不准确

正常情况下我们通过下面方式获取宽高PdfReader reader new PdfReader(file.getPath()); float width reader.getPageSize(1).getWidth(); float height reader.getPageSize(1).getHeight();但是这样获取的宽高是不准确的&#xff0c;永远都是 宽 > 高&#xff0c;也就是横…
阅读更多...
NodeJs学习日志（2）：windows安装使用node.js 安装express，suquelize，mysql，nodemon

NodeJs学习日志（2）：windows安装使用node.js 安装express，suquelize，mysql，nodemon

windows安装使用node.js 安装express&#xff0c;suquelize&#xff0c;mysql&#xff0c;nodemon 系统是win10&#xff0c;默认已经安装好nodejs与npm包名作用expressWeb应用框架suquelize数据库ORMmysql数据库nodemon代码热重载安装express 添加express生成器 npm add expres…
阅读更多...
VueCropper 图片裁剪组件在Vue项目中的实践应用

VueCropper 图片裁剪组件在Vue项目中的实践应用

VueCropper 图片裁剪组件在Vue项目中的实践应用 1. 组件介绍 VueCropper 是一个基于 Vue.js 的图片裁剪组件&#xff0c;它提供了丰富的图片裁剪功能&#xff0c;包括&#xff1a; 图片缩放、旋转、移动固定比例裁剪高质量图片输出多种裁剪模式选择 2. 安装与引入 首先需要安装…
阅读更多...
给同一个wordpress网站绑定多个域名的实现方法

给同一个wordpress网站绑定多个域名的实现方法

在WordPress网站上绑定多个域名&#xff0c;可以通过以下几种方法实现&#xff1a; 1. 修改wp-config.php文件 在wp-config.php文件中&#xff0c;找到define(‘WP_DEBUG’, false);&#xff0c;在其下方添加以下代码&#xff1a; define(WP_SITEURL, http:// . $_SERVER[HT…
阅读更多...
HarmonyOS分布式开发实战：打造跨设备协同应用

HarmonyOS分布式开发实战：打造跨设备协同应用

&#x1f4d6; 文章目录 第一章&#xff1a;HarmonyOS分布式架构揭秘第二章&#xff1a;跨设备协同的核心技术第三章&#xff1a;开发环境搭建与配置第四章&#xff1a;实战项目&#xff1a;智能家居控制系统第五章&#xff1a;数据同步与状态管理第六章&#xff1a;性能优化与…
阅读更多...
用 Enigma Virtual Box 把 Qt 程序压成单文件 EXE——从编译、收集依赖到一键封包

用 Enigma Virtual Box 把 Qt 程序压成单文件 EXE——从编译、收集依赖到一键封包

关键词&#xff1a;Qt、windeployqt、Enigma Virtual Box、单文件、绿色软件 为什么要打成单文件&#xff1f; 传统做法&#xff1a;用 windeployqt 把依赖拷进 release 目录&#xff0c;发给用户一个文件夹&#xff0c;文件又多又乱。理想做法&#xff1a;把整个目录压成一个…
阅读更多...
unity中实现选中人物脚下显示圆形标识且完美贴合复杂地形（如弹坑） 的效果

unity中实现选中人物脚下显示圆形标识且完美贴合复杂地形（如弹坑） 的效果

要实现人物脚下圆形 完美贴合复杂地形&#xff08;如弹坑&#xff09; 的效果&#xff0c;核心思路是 「动态生成贴合地面的 Mesh」 —— 即根据地面的高度场实时计算环形顶点的 Y 坐标&#xff0c;让每个顶点都 “贴” 在地面上。核心逻辑&#xff1a;确定环形范围&#xff1a…
阅读更多...
引领GameFi 2.0新范式：D.Plan携手顶级财经媒体启动“龙珠创意秀”

引领GameFi 2.0新范式：D.Plan携手顶级财经媒体启动“龙珠创意秀”

在GameFi赛道寻求新突破的今天&#xff0c;一个名为Dragonverse Plan&#xff08;D.Plan&#xff09;的项目正以其独特的经济模型和宏大愿景&#xff0c;吸引着整个Web3社区的目光。据悉&#xff0c;D.Plan即将联合中文区顶级加密媒体金色财经与非小号&#xff08;Feixiaohao&a…
阅读更多...
通信算法之307：fpga之时序图绘制

通信算法之307：fpga之时序图绘制

时序图绘制软件 一. 序言 在FPGA设计过程中&#xff0c;经常需要编写设计文档&#xff0c;其中&#xff0c;不可缺少的就是波形图的绘制&#xff0c;可以直接截取Vivado或者Modelsim平台实际仿真波形&#xff0c;但是往往由于信号杂乱无法凸显重点。因此&#xff0c;通过相应软…
阅读更多...
计网学习笔记第3章 数据链路层（灰灰题库）

计网学习笔记第3章 数据链路层（灰灰题库）

题目 11 单选题 下列说法正确的是______。 A. 路由器具有路由选择功能&#xff0c;交换机没有路由选择功能 B. 三层交换机具有路由选择功能&#xff0c;二层交换机没有路由选择功能 C. 三层交换机适合异构网络&#xff0c;二层交换机不适合异构网络 D. 路由器适合异构网络&…
阅读更多...
SQL的LEFT JOIN优化

SQL的LEFT JOIN优化

原sql&#xff0c;一个base表a,LEFT JOIN三个表抽数 SELECT ccu.*, ctr.*, om.*, of.* FROM ods.a ccu LEFT JOIN ods.b ctr ON ccu.coupon_code ctr.coupon_code AND ctr.is_deleted 0 LEFT JOIN ods.c om ON ctr.bill_code om.order_id AND om.deleted 0 LEFT JOIN ods.…
阅读更多...
Redis 核心概念、命令详解与应用实践：从基础到分布式集成

Redis 核心概念、命令详解与应用实践：从基础到分布式集成

目录 1. 认识 Redis 2. Redis 特性 2.1 操作内存 2.2 速度快 2.3 丰富的功能 2.4 简单稳定 2.5 客户端语言多 2.6 持久化 2.7 主从复制 2.8 高可用 和 分布式 2.9 单线程架构 2.9.1 引出单线程模型 2.9.2 单线程快的原因 2.10 Redis 和 MySQL 的特性对比 2.11 R…
阅读更多...
【Day 18】Linux-DNS解析

【Day 18】Linux-DNS解析

目录 一、DNS概念 1、概念和作用 2、域名解析类型 3、 软件与服务 4、DNS核心概念 区域 记录 5、查询类型 6、分层结构 二、DNS操作 配置本机为DNS内网解析服务器 &#xff08;1&#xff09;修改主配置文件 &#xff08;2&#xff09;添加区域 正向解析区域&#xff1a; …
阅读更多...
Python 中 OpenCV (cv2) 安装与使用介绍

Python 中 OpenCV (cv2) 安装与使用介绍

Python 中 OpenCV (cv2) 安装与使用详细指南 OpenCV (Open Source Computer Vision Library) 是计算机视觉领域最流行的库之一。Python 通过 cv2 模块提供 OpenCV 的接口。 一、安装 OpenCV 方法 1&#xff1a;基础安装&#xff08;推荐&#xff09; # 安装核心包&#xff0…
阅读更多...
微软WSUS替代方案

微软WSUS替代方案

微软WSUS事件回顾2025年7月10日&#xff0c;微软最新确认Windows Server Update Services&#xff08;WSUS&#xff09;出现了问题&#xff0c;导致IT管理员无法正常同步和部署Windows更新。WSUS是允许管理员根据策略配置&#xff0c;将更新推送到特定计算机&#xff0c;并优化…
阅读更多...
最新文章

Copyright @ 2022~2023