最短路径的典型用途:
交通网络的问题——从甲地到乙地之间是否有公路连通?
在有多条通路的情况下,哪一条路最短?
交通网络用有向网来表示:顶点——表示地点,弧——表示两个地点有路连通,弧上的权值——表示两地点之间的距离、交通费或途中所花费的时间等。
如何能够使一个地点到另一个地点的运输时间最短或运费最省?这就是一个求两个地点间的最短路径问题。
问题抽象:
在有向网中A点(源点)到达B点(终点)的多条路径中,寻找一条各边权值之和最小的路径,即最短路径。
最短路径与最小生成树不同,路径上不一定包含n个顶点,也不一定包含n - 1条边。
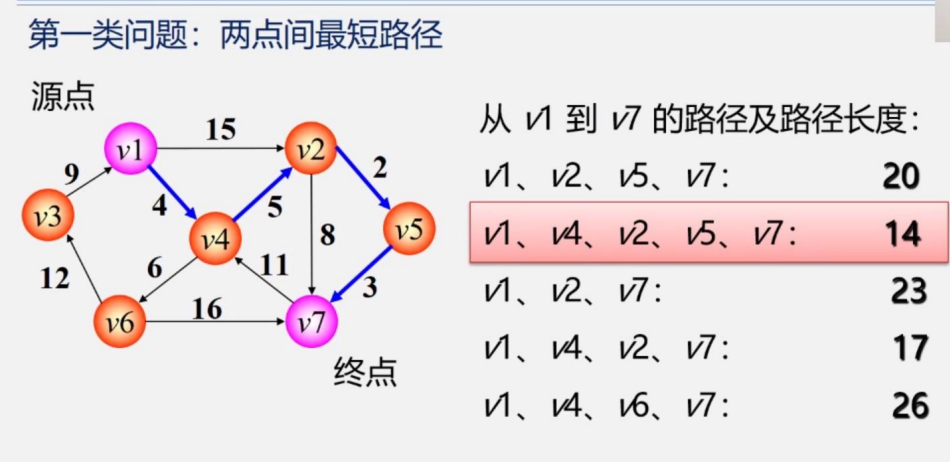
第一类问题是求两点间的最短路径:下图是两点间的距离,求最短路径,比如是从V1到V7,我们将所有可能的路径一一罗列并求权值之和,比较大小
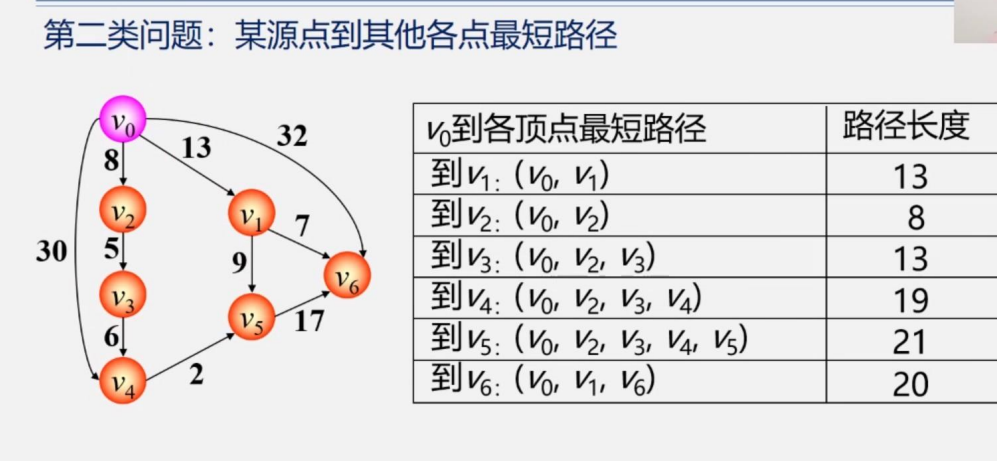
第二类问题是求某源点到其他个点的最短路径:此时源点是任取的,看你想要哪个作为起点
下图中,比如由V0到V4的最短路径,有两条,一条是V0-V2-V3-V4=8+5+6=19,还有一条是V0直接到V4,权值是30,很明显19更小,所有19填入表中,以此类推,不再赘述
两种常见的最短路径问题:
一、单源最短路径:用Dijkstra(迪杰斯特拉)算法
二、所有顶点间的最短路径:用Floyd(弗洛伊徳)算法
接下来我们来分析迪杰斯特拉算法
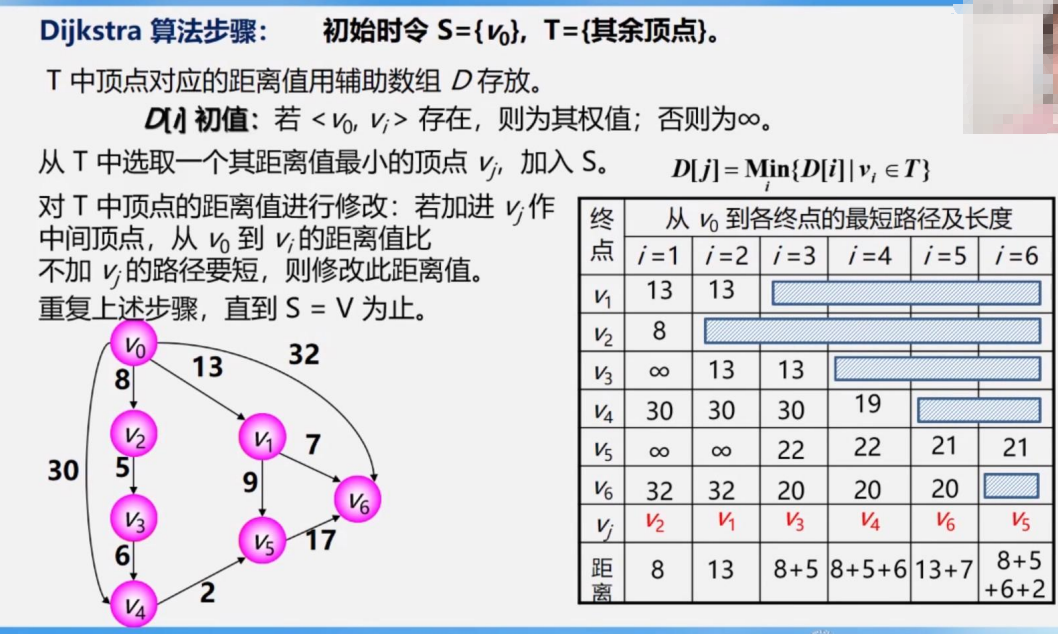
如下图表,i=1所在的列,是指的V0到其他所有顶点的权值,如果没有直达的边(一条),记为∞
1.从VO到V1,权值为13,所以我们在V1所在行的第一个表格上填13,V0到V2权值为8,所以在V2所在行第一个表格填8,以此类推,V0到V4为30,V0到V6为32,其余填∞
2.找出填好的这一列(i=1所在的列)最小的权值,填到距离那行,也就是权值为8最小,对应的是V2,将V2填入Vj那一行,于是V2所在行划去,因为我们已经找到到达V2的最小距离
3.接着,从V0和VO-V2出发,继续寻找最短路径,V0-V1依然不变是13,而V0-V2到V3,权值为8+5=13,除此之外无从V0/V2出发的路径能到达V3,所以V3的值改为13,V4没有V0-V2能直接到的边(就是走一条边就能到),所以依然是30不变,以此类推
4.我们发现,此时13是最小路径,把第一个13(V1)放入距离和Vj中,划去V1所在行,此后不再需要比较V1和V2的路径
以此类推,不再赘述
弗洛依德 (Floyd) 算法思想:
逐个顶点试探 ,从 Vi到 Vj 的所有可能存在的路径中 ,选出一条长度最短的路径
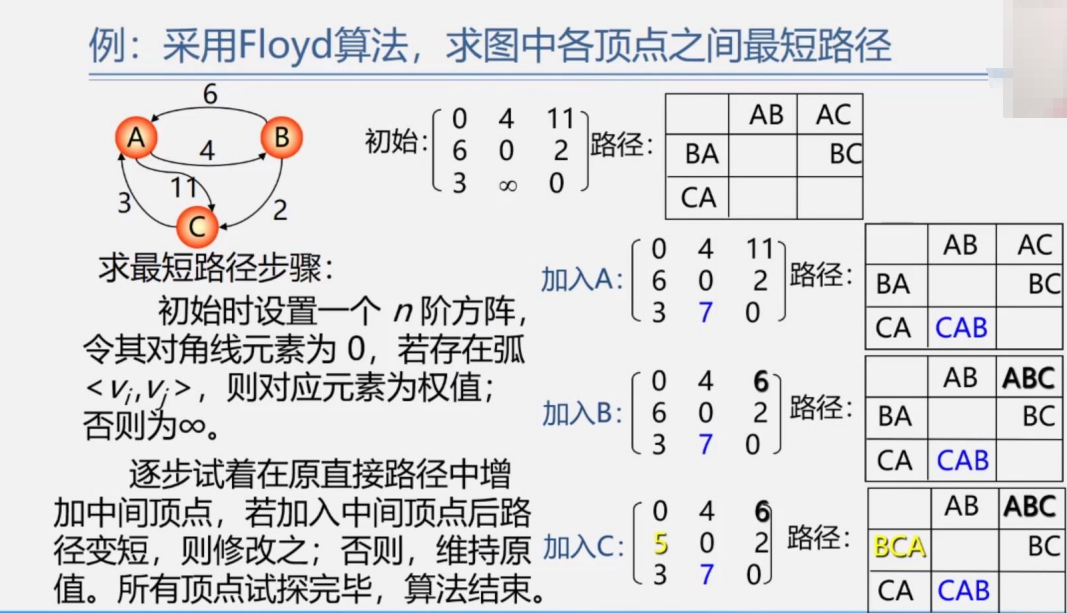
我们一 一分析一下这道题
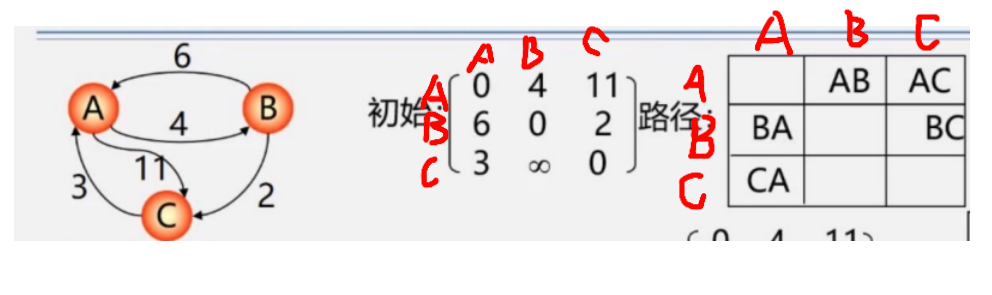
从A->B,权值是4,A->C是11,以此类推,主对角线均为0(因为A到A,B到B,C到C均无边)
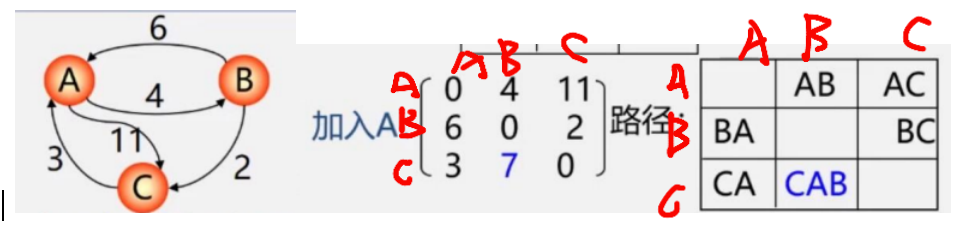
加入A的意思是,比如从B到C,那加入A就是B-A-C的路径,是6+11=17>2,所以BC不动
分析C到B,加入A就是CAB=3+4=7<∞,所以改为7
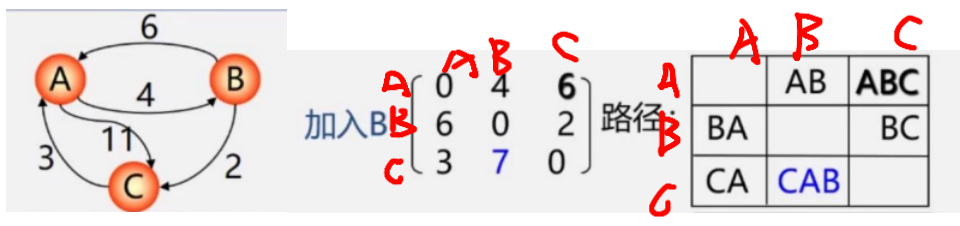
加入B,我们分析A到C,ABC=4+2=6<11,所以改为6
分析C到A,CBA,C没有直接到B的,所以不必改
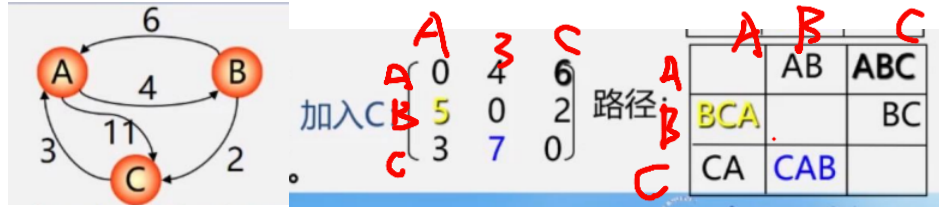
加入C,我们分析BA,B-C-A=2+3=5<6,所以改为5
总结:加入谁,谁所在的行先不变,对角线永远是0





Gemini Agent 使用指南)
)

 远程登录VirtualBox中的Ubuntu24.04,显示图形化(GUI)界面)


)



 视频教程 - 词云图-微博评论用户词云图实现)



