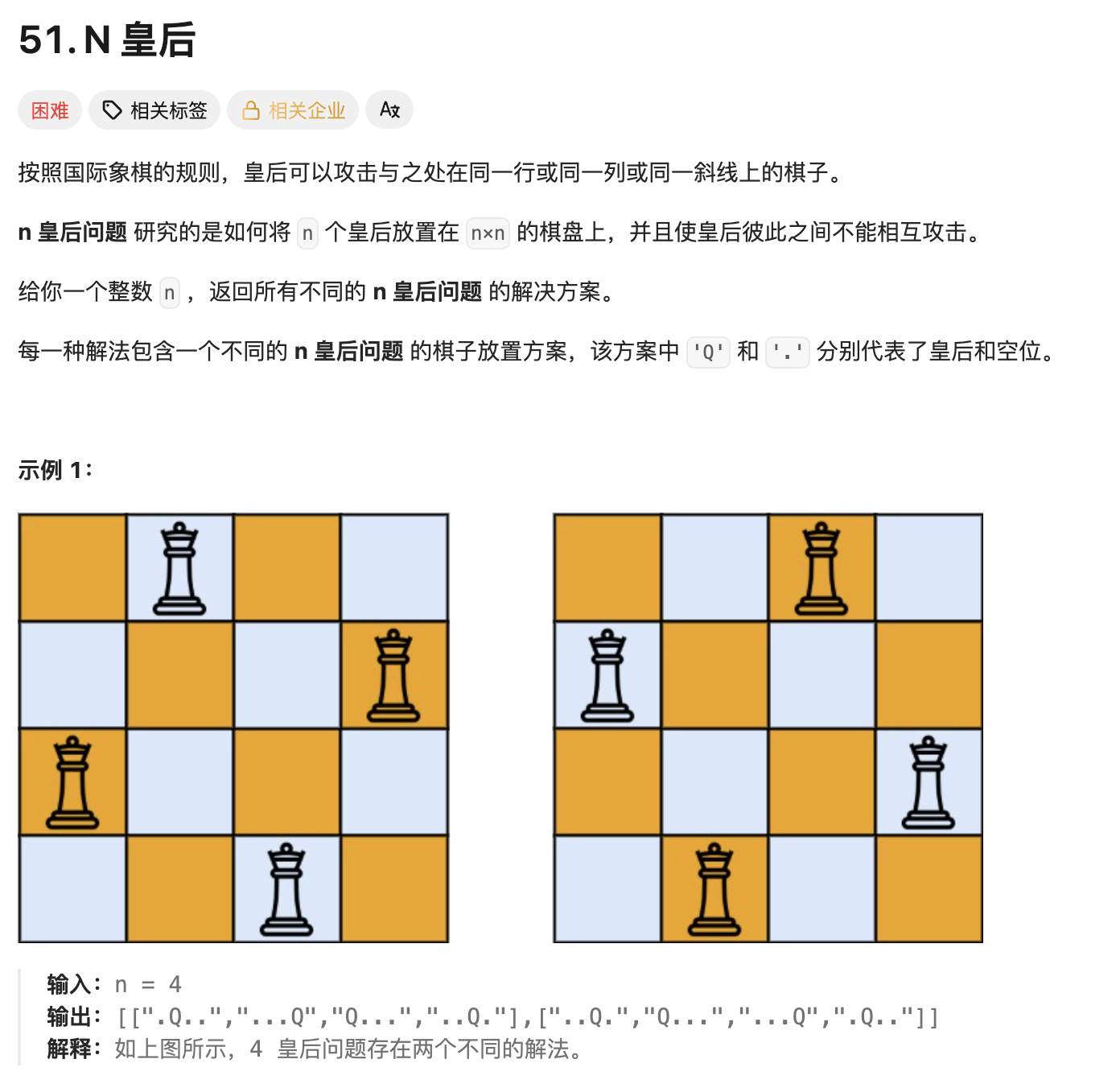
1.题目描述

2.思路

二维数组集合
(1）N皇后规则
1）不能同行（同一行不能出现2个皇后）
2）不能同列（同一列不能出现2个皇后）
3）不能说45度或135度（斜对角线不能出现2个皇后）

n代表树高，也就是嵌套for循环的行数

3.代码实现

class Solution {public List<List<String>> solveNQueens(int n) {//三维结果数组,用于存储最终所有符合条件的解法。List<List<String>> result=new ArrayList<>();//初始化一个 n x n 的棋盘，用字符数组表示char[][] board=new char[n][n];//先构建棋盘，用.填满,表示该位置为空。for(int i=0;i<n;i++){for(int j=0;j<n;j++){board[i][j]='.';}}//1.确定递归函数的参数backTracking(result,board,0,n);return result;}   //1.确定递归函数的参数//    - solutions: 存储所有解法的列表。//    - board: 当前的棋盘状态。//    - row: 当前正准备放置皇后的行号。从第 0 行开始，调用回溯函数//    - n: 棋盘的大小。//     void backTracking（private void backTracking(List<List<String>>result,char[][]board,int row,int n){//2.确定终止条件,遍历到最后一行if(row==n){result.add(strContruct(board));return;}//3.单层搜索条件for(int col=0;col<n;col++){if(isValid(board,row,col,n)){board[row][col]='Q';// “每一行只放一个皇后” 的规则。因为函数每次被调用时，只处理 row 这一行。在这一行的 for 循环里，它会尝试在 (row, 0), (row, 1), (row, 2)... 等位置放皇后，但一次只会放一个。放下一个之后，它就立刻递归到 row + 1 行去了，所以，“不同行” 是由这个递归结构保证的。backTracking(result,board,row+1,n);board[row][col]='.';}}}private boolean isValid(char[][]board,int row,int col,int n){//不能同列for(int i=0;i<row;i++){if(board[i][col]=='Q'){return false;}}//不能是对角线 45度for(int i=row-1, j=col-1;i>=0&&j>=0;i--,j--){if(board[i][j]=='Q'){return false;}}for(int i=row-1,j=col+1;i>=0&&j<n;i--,j++){if(board[i][j]=='Q'){return false;}}return true;}private List<String> strContruct(char[][] board){// 将 char[][] 棋盘转换为 List<String> 的格式List<String> res=new ArrayList<>();for(int i=0;i<board.length;i++){String curstr=new String(board[i]);res.add(curstr);}return res;}}