C++---双指针

在C++编程中，双指针算法是一种高效的解题思路，其核心是通过设置两个指针（或索引）遍历数据结构（如数组、链表、字符串等），利用指针的移动规则减少无效操作，从而将时间复杂度从暴力解法的O(n²)优化至O(n)或O(n log n)。这种算法广泛应用于链表操作、数组处理、字符串匹配等场景。

一、双指针算法的核心思想

双指针算法的本质是通过两个指针的协同移动，缩小问题的处理范围。与暴力解法中嵌套循环的“盲目遍历”不同，双指针的移动具有明确的逻辑（如基于数据的有序性、结构特性等），从而避免冗余计算。

其核心优势体现在：

时间优化：将多层循环转化为单层遍历，降低时间复杂度；
空间优化：多数情况下无需额外空间（原地操作），空间复杂度可保持O(1)；
逻辑清晰：通过指针的移动规则直观反映问题的解决思路。

二、双指针的常见类型及应用场景

根据指针的移动方向和作用，双指针可分为三大类：快慢指针、左右指针、同向指针。以下结合具体场景详细讲解。

（一）快慢指针（Floyd’s Tortoise and Hare）

快慢指针指两个指针以不同速度遍历数据结构（如链表中，快指针每次走2步，慢指针每次走1步）。其核心应用是处理链表中的环问题和查找特定位置（如中间节点）。

1. 链表环检测（LeetCode 141）

问题：判断一个单链表是否存在环。
暴力解法：用哈希表记录访问过的节点，若重复访问则有环，时间O(n)但空间O(n)。
双指针解法：

设快指针fast和慢指针slow，初始均指向头节点；
fast每次移动2步，slow每次移动1步；
若链表有环，fast会先进入环并绕环移动，最终与slow在环内相遇；
若fast到达nullptr，则无环。

代码实现：

struct ListNode {int val;ListNode *next;ListNode(int x) : val(x), next(nullptr) {}
};bool hasCycle(ListNode *head) {if (head == nullptr || head->next == nullptr) return false;ListNode *slow = head;ListNode *fast = head->next; // 初始错开，避免直接相遇while (slow != fast) {if (fast == nullptr || fast->next == nullptr) return false;slow = slow->next;       // 慢指针走1步fast = fast->next->next; // 快指针走2步}return true;
}

时间复杂度：O(n)（无环时fast走n/2步；有环时相遇前slow最多走n步）。
空间复杂度：O(1)（仅用两个指针）。

2. 寻找环的入口（LeetCode 142）

问题：若链表有环，找到环的入口节点。
算法思路：

先用快慢指针判断有环，记录相遇点meet；
让slow从头节点出发，fast从meet出发，两者均每次走1步；
两指针再次相遇的节点即为环的入口。

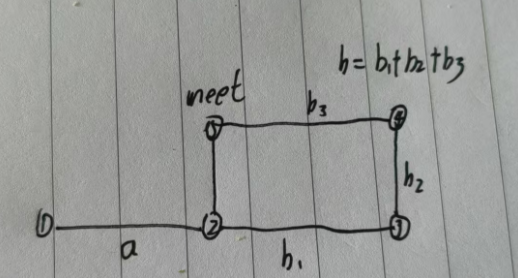
原理：设头节点到入口距离为a，入口到相遇点距离为b，环长为c。则相遇时：

slow走了a + b；
fast走了a + b + k*c（绕环k圈）；
因fast速度是slow的2倍，故2*(a + b) = a + b + k*c → a = k*c - b b=k*c-a。
因此，slow从头部走a步，与fast从meet走k*c - b步（等价于绕环k圈后回到入口）相遇。

重置slow = 0,fast仍在meet处（等价于初始走了a+b），当slow=a(slow走了a步)，fast=a+b+kc-b=a+kc，所以a,b在环的入口相遇

代码实现：

ListNode *detectCycle(ListNode *head) {if (head == nullptr) return nullptr;ListNode *slow = head, *fast = head;// 第一步：找到相遇点do {if (fast->next == nullptr || fast->next->next == nullptr) return nullptr;slow = slow->next;fast = fast->next->next;} while (slow != fast);// 第二步：寻找入口slow = head;while (slow != fast) {slow = slow->next;fast = fast->next;}return fast;
}

3. 寻找链表的中间节点（LeetCode 876）

问题：返回单链表的中间节点（若长度为偶数，返回第二个中间节点）。
算法思路：

快指针每次走2步，慢指针每次走1步；
当fast到达尾节点时，slow恰好指向中间节点。

代码实现：

ListNode* middleNode(ListNode* head) {ListNode *slow = head, *fast = head;while (fast != nullptr && fast->next != nullptr) {slow = slow->next;fast = fast->next->next;}return slow;
}

（二）左右指针（相向指针）

左右指针指两个指针分别从数据结构的两端出发，相向而行（左指针从左向右，右指针从右向左），多用于有序数组/字符串的处理。其核心是利用数据的有序性，通过指针移动排除无效解。

1. 两数之和（有序数组版，LeetCode 167）

问题：给定有序数组nums和目标值target，找到两个数使得和为target，返回索引（下标从1开始）。
暴力解法：嵌套循环遍历所有组合，时间O(n²)。
双指针解法：

左指针left初始指向0，右指针right指向n-1；
计算当前和sum = nums[left] + nums[right]：
- 若sum == target，返回[left+1, right+1]；
- 若sum > target，说明右指针太大，right--；
- 若sum < target，说明左指针太小，left++。

原理：数组有序保证了指针移动的有效性——当sum > target时，减小右指针可降低总和；当sum < target时，增大左指针可提高总和，无需检查其他组合。

代码实现：

vector<int> twoSum(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1;while (left < right) {int sum = nums[left] + nums[right];if (sum == target) {return {left + 1, right + 1};} else if (sum > target) {right--;} else {left++;}}return {-1, -1}; // 题目保证有解，此行为冗余
}

时间复杂度：O(n)，空间复杂度O(1)。

2. 反转字符串（LeetCode 344）

问题：原地反转字符串（如["h","e","l","l","o"]→["o","l","l","e","h"]）。
算法思路：

左指针left指向0，右指针right指向n-1；
交换nums[left]与nums[right]，然后left++、right--，直到left >= right。

代码实现：

void reverseString(vector<char>& s) {int left = 0, right = s.size() - 1;while (left < right) {swap(s[left], s[right]);left++;right--;}
}

3. 二分查找（本质是左右指针的变体）

二分查找中，left和right指针分别指向搜索范围的两端，通过比较中间值与目标值，不断缩小范围，本质是左右指针的“跳跃式移动”。

代码实现：

int search(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1;while (left <= right) {int mid = left + (right - left) / 2; // 避免溢出if (nums[mid] == target) return mid;else if (nums[mid] < target) left = mid + 1;else right = mid - 1;}return -1;
}

（三）同向指针（一前一后指针）

同向指针指两个指针从同一端出发，沿相同方向移动（通常一个在前“探索”，一个在后“记录”），多用于数组去重、子数组/子串问题。

1. 删除有序数组中的重复项（LeetCode 26）

问题：原地删除有序数组中的重复元素，返回新长度（如[1,1,2]→长度2，数组变为[1,2]）。
算法思路：

慢指针slow记录有效元素的尾位置（初始0）；
快指针fast遍历数组（初始1）；
若nums[fast] != nums[slow]，说明找到新元素，slow++并将nums[fast]复制到nums[slow]；
最终slow + 1为新长度。

代码实现：

int removeDuplicates(vector<int>& nums) {if (nums.empty()) return 0;int slow = 0;for (int fast = 1; fast < nums.size(); fast++) {if (nums[fast] != nums[slow]) {slow++;nums[slow] = nums[fast];}}return slow + 1;
}

2. 移动零（LeetCode 283）

问题：将数组中的0移到末尾，保持非零元素的相对顺序（如[0,1,0,3,12]→[1,3,12,0,0]）。
算法思路：

慢指针slow记录非零元素的尾位置（初始0）；
快指针fast遍历数组，若nums[fast] != 0，则交换nums[slow]与nums[fast]，slow++；
遍历结束后，slow及之后的位置全部赋0。

代码实现：

void moveZeroes(vector<int>& nums) {int slow = 0;for (int fast = 0; fast < nums.size(); fast++) {if (nums[fast] != 0) {swap(nums[slow], nums[fast]);slow++;}}// 剩余位置补0（可选，因原数组0已被交换到后面）for (int i = slow; i < nums.size(); i++) {nums[i] = 0;}
}

3. 滑动窗口（同向指针的高级应用）

滑动窗口是同向指针的典型场景，用于解决子数组/子串的最值问题（如最长、最短、包含特定元素等）。其核心是用left和right指针维护一个“窗口”，通过移动right扩张窗口，移动left收缩窗口，在O(n)时间内找到最优解。

示例：长度最小的子数组（LeetCode 209）
问题：给定数组nums和目标值s，找到和≥s的最短子数组长度（若无则返回0）。

算法思路：

left和right初始均为0，sum记录窗口内元素和；
移动right，将nums[right]加入sum；
当sum ≥ s时，尝试移动left缩小窗口，更新最小长度；
重复直至right遍历结束。

代码实现：

int minSubArrayLen(int s, vector<int>& nums) {int n = nums.size();int min_len = INT_MAX;int left = 0, sum = 0;for (int right = 0; right < n; right++) {sum += nums[right];// 收缩窗口while (sum >= s) {min_len = min(min_len, right - left + 1);sum -= nums[left];left++;}}return min_len == INT_MAX ? 0 : min_len;
}