引言

欢迎来到本系列的第十一篇！在我们通过“最大深度”问题初步领略了树的递归之美后，今天我们将面对一个更能体现递归“分治”思想的经典问题——LeetCode 226. 反转二叉树。

这道题在面试界的地位非同凡响，它因 Homebrew 的作者 Max Howell 在 Google 面试时被这道题难住，并愤然发推吐槽而闻名于世。但这道题真的那么难吗？

当你第一次看到这道题，你可能会发现它具有一种“镜像”的对称性，并且可以分解成更小的、相同的问题。这正是解决它的正确方向！但如何将这种直觉转化为清晰、正确的代码呢？

本文将带你一起：

1. 分析并完善关于“完全二叉树”、“终止条件”等问题的初步想法。

2. 深入理解递归如何像一个“自上而下的命令链”，优雅地完成整棵树的反转。

3. 掌握解决这类树结构修改问题的通用递归模板。

---

一、题目呈现

• 题目编号：226. 反转二叉树

• 题目难度：简单

• 题目链接：226. 反转二叉树 - 力扣 (LeetCode)

• 题目描述：

  给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

• 示例：

  • 输入: root = [4,2,7,1,3,6,9]

  • 输出: [4,7,2,9,6,3,1]

  反转前：

        4/ \2   7/ \ / \1  3 6  9

反转后：

      4/ \7   2/ \ / \9  6 3  1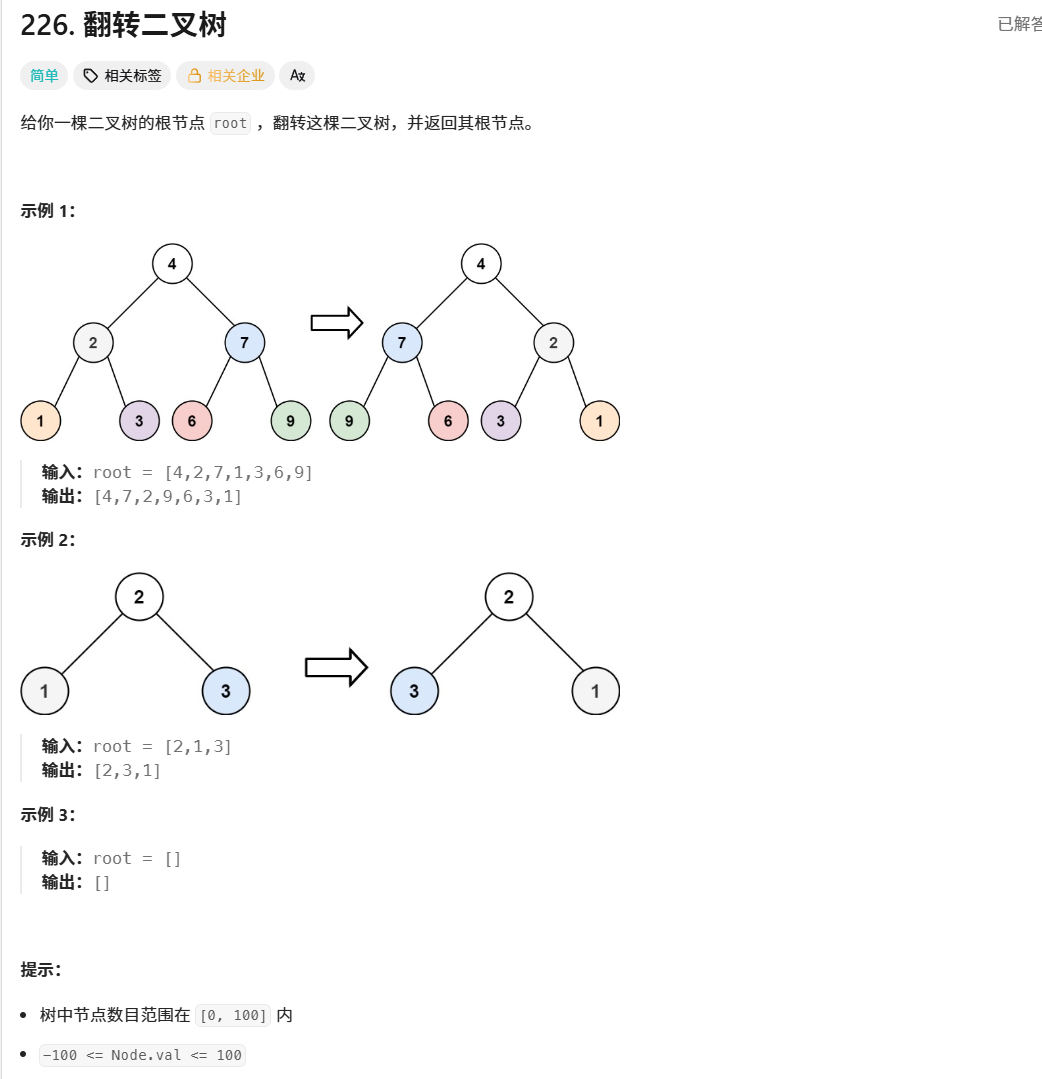

二、我的思考：递归直觉的打磨

（这里完全采用你的笔记思路）

看到这棵树，我的第一反应是：这个问题可以拆分成更小的相同问题。比如，要反转整棵以 4 为根的树，似乎可以先反转以 2 为根的左子树，再反转以 7 为根的右子树，最后再做点什么。这种“分治”的感觉，让我立刻想到了递归。

我的初步想法是：

1. 终止条件：当递归到最左边的叶子节点，它的 left 是 nullptr 时，就应该停止了。

2. 核心操作：在某个节点，我需要交换它的 left 和 right 指针，这需要一个临时变量来暂存。

但我很困惑：我应该按什么顺序去递归呢？先一路递归到最左边，再处理右边吗？那返回的顺序好像不对。而且，函数最后应该返回什么？是节点的值 val 吗？

你的思考过程非常棒！你已经抓住了递归和交换这两个核心要素。现在，我们来逐一打磨这些想法，扫清困惑。

1. 关于终止条件：只考虑 left 为 nullptr 是不够的。一个更通用、更安全的终止条件是：当递归遇到的当前节点 root 本身是 nullptr 时，就返回。因为我们不能对一个空节点做任何操作。

2. 关于返回值：函数的签名是 TreeNode* invertTree(TreeNode* root)，它要求我们返回一个 TreeNode* 指针。我们的任务是修改树的结构，并最终返回修改后整棵树的根节点。

3. 关于递归顺序：这正是本题的精髓！答案是，对于“反转”这个操作，先处理当前节点，再递归子节点（前序遍历） 的思路是最直观的。

---

三、豁然开朗：递归的“自顶向下”反转模型

让我们把反转过程想象成一个**“将军下令”**的指挥链。

将军（当前根节点 root）的任务只有两件：

1. 先行动：交换自己直接指挥的两个师长（左子节点 left 和右子节点 right）的位置。

2. 再下令：对换完位置的两位师长分别说：“现在，你们各自去把手下的部队（你们的子树）也全部反转一遍！”

这个命令会从最高级的将军 root，一层层地传递下去，直到最底层的士兵（叶子节点）。当士兵接到命令，发现自己手下没有兵（子节点为 nullptr）时，他什么也不做，直接报告“任务完成”。当所有士兵都报告完成后，整棵树的“镜像反转”就完成了。

C++ 最优代码与详解

这个“将军下令”的模型，可以被直接翻译成极其简洁的递归代码。

完整代码

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}* };*/
class Solution {
public:TreeNode* invertTree(TreeNode* root) {// 1.if (root == nullptr) {return nullptr;}// --- 核心操作区 (前序遍历位置) ---// 2.TreeNode* temp = root->left;root->left = root->right;root->right = temp;// 3.invertTree(root->left);invertTree(root->right);// 4.return root;}
};

代码逐点解释

1. if (root == nullptr)
   递归的终止条件 (Base Case)。如果当前节点为空，它没有子节点可以交换，直接返回 nullptr。这是递归能够停止的保证。

2. TreeNode* temp = ...;
   核心交换操作。我们先用一个临时指针 temp 暂存左子节点的地址，然后将右子节点赋给左指针，最后将暂存的地址赋给右指针，完成了对当前节点 root 的直接子节点的交换。

3. invertTree(root->left); invertTree(root->right);
   分治与递归。这是“将军下令”的步骤。我们对已经交换过来的新左子树和新右子树，分别进行递归调用。我们完全信任这两个递归调用能完美地反转它们各自内部的所有结构。

4. return root;
   返回结果。在完成了本层的交换和对子树的递归反转之后，当前 root 节点下的整棵子树都已经完成了反转。我们将这个 root 返回给它的上层调用。最终，最顶层的调用会返回整棵树的新根节点（其实还是原来的那个根节点，但它的结构已经被改变了）。

---

四、总结与收获

• 复杂度分析：我们恰好访问了树中的每一个节点一次来执行交换操作。因此，时间复杂度为 O(n)，其中 n 是节点的总数。递归调用栈的深度最坏情况下等于树的高度，因此空间复杂度为 O(h)。

• 核心思想：对于树这种具有天然递归结构的题目，分治思想是解决问题的金钥匙。将一个大问题（反转整棵树）分解为三个小步骤：处理当前节点、递归处理左子树、递归处理右子树。

• 关键技巧：理解递归函数调用的本质。当你写 invertTree(root->left) 时，你要在脑中形成一种“信任”——相信这个函数一定会返回一个已经完全反转好的左子树，而无需关心其内部细节。这种“定义与信任”是掌握递归的关键。