《离散数学学习指导与习题解析（第2版）》是屈婉玲、耿素云、张立昂编著的《离散数学（第2版）》的配套参考书，旨在为学生提供系统的学习指导和丰富的习题解析。本书内容全面，涵盖数理逻辑、集合论、代数结构、组合数学、图论和初等数论六大模块，共19章。每章均包括内容提要、基本要求、习题课、习题与解答或提示、小测验，并附有四套模拟试题及详细解答。

我用夸克网盘给你分享了「离散数学-屈婉玲-第1、2版-教材+学习指导」，链接：https://pan.quark.cn/s/3b3f72969991

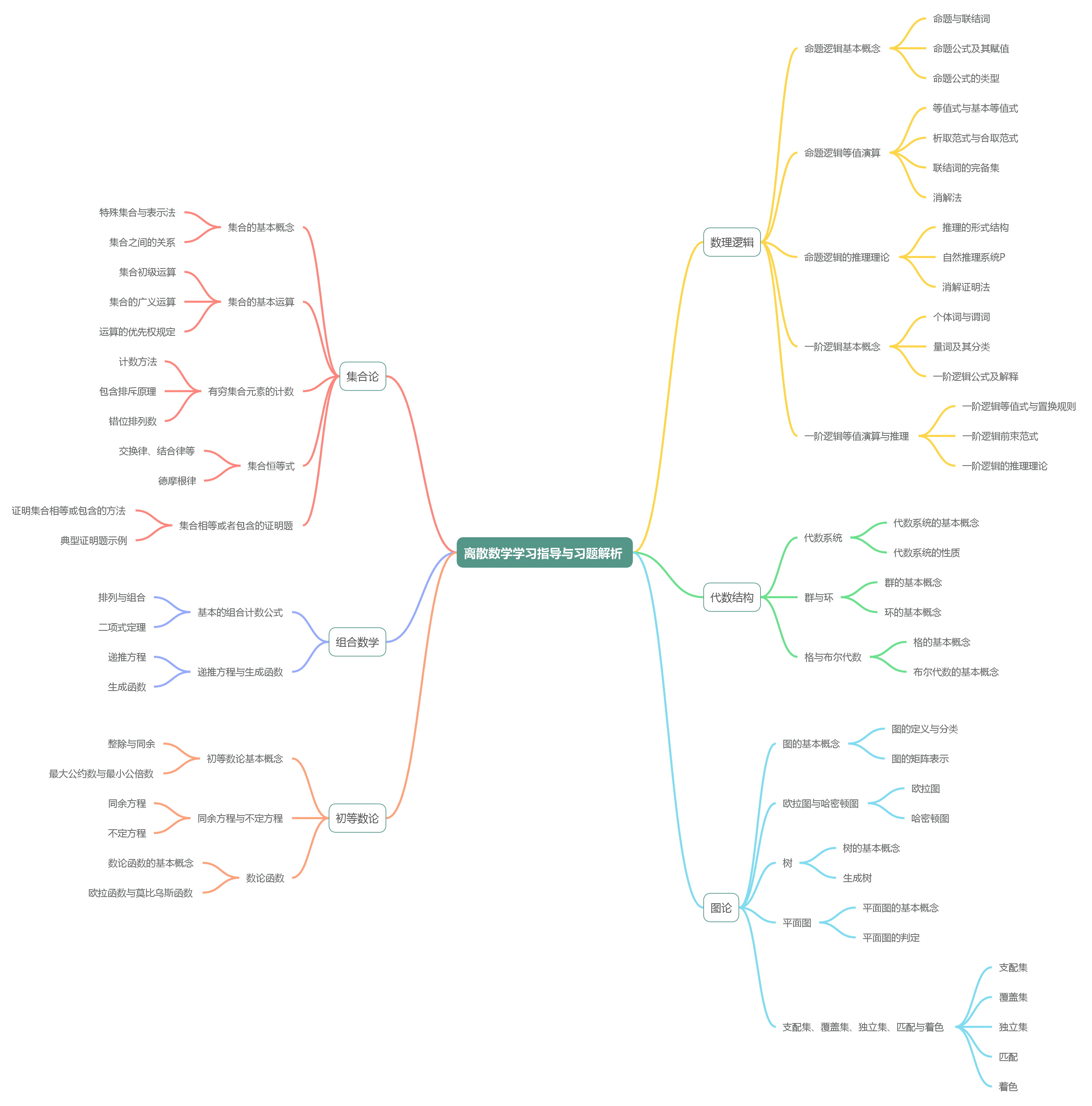
一、内容结构与特点

1. 数理逻辑（第1-5章）

   • 命题逻辑：介绍命题、联结词、命题公式、赋值、命题公式的类型（重言式、矛盾式、可满足式）及其判断方法。
   • 一阶逻辑：涵盖一阶逻辑的基本概念、等值演算与推理，强调逻辑推理方法与公式的类型判断。
   • 每章均配有详细的习题解析，帮助学生掌握命题符号化、真值表、等值演算、主析取范式等核心概念。

2. 集合论（第6-8章）

   • 集合代数：包括集合的基本运算、幂集、集合恒等式。
   • 二元关系：讨论关系的性质、关系的闭包运算、等价关系与偏序关系。
   • 函数：介绍函数的定义、分类、复合函数与反函数。
   • 每章内容通过大量例题与解析，帮助学生理解集合、关系与函数之间的逻辑联系。

3. 代数结构（第9-11章）

   • 代数系统：讲解代数结构的基本概念、同态与同构。
   • 群与环：包括群的定义、性质、子群、环的定义与类型。
   • 格与布尔代数：介绍格的基本性质、布尔代数的应用。
   • 强调代数系统的结构分析和运算性质，帮助学生建立抽象思维能力。

4. 组合数学（第12-13章）

   • 基本组合计数公式：涵盖排列、组合、二项式定理、鸽巢原理。
   • 递推方程与生成函数：介绍递推关系的建立与求解、生成函数的应用。
   • 通过典型例题训练学生解决实际组合问题的能力。

5. 图论（第14-18章）

   • 图的基本概念：包括图的表示、连通性、欧拉图、哈密顿图。
   • 树：讲解树的性质、生成树、最小生成树算法。
   • 平面图：介绍平面图的定义、欧拉公式、库拉托夫斯基定理。
   • 支配集、覆盖集、独立集、匹配与着色：讨论图的特殊子集与图的着色问题。
   • 通过图论模型，训练学生解决网络优化、路径规划等实际问题。

6. 初等数论（第19章）

   • 涉及整除、最大公约数、最小公倍数、素数、同余、模运算、中国剩余定理等基础内容。
   • 强调数论在计算机科学中的应用，如密码学、算法设计。

二、教学组织与学习资源

• 章节结构：每章均包含内容提要、基本要求、习题课、习题与解答或提示、小测验，结构清晰，便于学生循序渐进学习。
• 模拟试题：全书最后提供四套综合性模拟试题及详细解答，覆盖各章节重点内容，帮助学生进行阶段性检测。
• 配套性：作为主教材的配套参考书，本书与主教材同步更新，新增了消解证明法、中国邮递员问题、加法器设计、进程代数建模、全同态加密等现代应用实例，增强学习的实践性与前沿性。

三、作者分工与修订说明

• 耿素云：完成第1-5章、第14~18章；
• 屈婉玲：完成第6~13章；
• 张立昂：完成第19章。
• 本书在第1版基础上进行了修订，更新了部分例题与习题，补充了多个重要应用实例，进一步优化了文字表述，提升可读性与实用性。