掌握数字世界的律动：时域离散信号与系统基础

想象一下，你用手机拍了一张照片，或者听了一首MP3歌曲。这些图片和声音，原本都是连续变化的模拟信号，但为什么它们能被你的手机存储和处理呢？秘密就在于“数字化”。在这个过程中，“时域离散信号”和“时域离散系统”扮演了主角。

简单来说，时域离散信号就是“打散”了的信号，它只在特定的、不连续的时间点上有值；而时域离散系统，就是处理这些“打散”信号的机器或算法。理解它们，是推开数字信号处理大门的第一步。

走进数字世界：离散时间信号 (序列)

在模拟世界里，信号是连续的，就像一条平滑的曲线，在任何一个时间点上你都能找到它的值。但在数字世界里，我们无法处理无限多的信息，所以必须对信号进行“抽样”，只在特定的时间点上进行测量。这些测量得到的、按照时间顺序排列的数值，就构成了离散时间信号，在DSP中，我们更常用一个更专业的词——序列（Sequence） 来称呼它。

什么是离散时间信号？

一个离散时间信号，通常用 $x(n)$ 来表示，其中 $n$ 是一个整数，代表了时间点。比如，当你每隔一秒测量一次房间的温度，你得到的就是一个离散时间信号：$T(0)$, $T(1)$, $T(2)$, …，这里的 $T(n)$ 就是在第 $n$ 秒测得的温度值。

与模拟信号 $x_a(t)$ 不同，$x(n)$ 不在任意时间 $t$ 上有值，它只在离散的整数时间点 $n$ 上有定义。

表示方法：

1. 集合法： 直接列出序列中所有有值的点及其对应的取值。
   例如： x ( n ) = { . . . , x ( − 1 ) , x ( 0 ) , x ( 1 ) , x ( 2 ) , . . . } x(n) = \{..., x(-1), x(0), x(1), x(2), ...\} x(n)={...,x(−1),x(0),x(1),x(2),...}。
   当序列只在有限个点有值时，通常会用一个箭头指示 $n=0$ 处的值，例如： x ( n ) = { 1 , 2 , 3 ‾ , 4 , 5 } x(n) = \{1, 2, \underline{3}, 4, 5\} x(n)={1,2,3​,4,5}，表示 $x(0)=3,x(-1)=2,x(-2)=1,x(1)=4,x(2)=5$。

2. 公式法： 使用数学公式来定义序列在每个时间点上的值。
   例如：$x(n)=n^{2}u(n)$，其中 $u(n)$ 是单位阶跃序列。这意味着当 $n<0$ 时，$x(n)=0$；当 $n\ge 0$ 时，$x(n)=n^2$。

3. 图形法 (序列波形图)： 将序列的每个值绘制在坐标轴上，横轴表示时间 $n$，纵轴表示序列值 $x(n)$。通常用垂直的直线或点来表示。

常见序列类型：数字世界的“基本粒子”

就像原子是构成物质的基本单位一样，在数字信号处理中，也有一些基础序列，它们是构成更复杂信号的“基本粒子”。

1. 单位脉冲序列 (Unit Impulse Sequence)

   • 定义：
     $$\delta (n)=\{\begin{array}{ll}1,& n=0\\ 0,& n\ne 0\end{array}$$
   • 意义：它就像一个瞬时敲击，只在 $n=0$ 时刻有一个非零值。
   • 应用：它是系统分析的基石。在DSP中，用一个单位脉冲序列作为输入，得到的输出就叫做单位脉冲响应，它就像一个系统的“指纹”，完全刻画了LTI系统的特性。

2. 单位阶跃序列 (Unit Step Sequence)

   • 定义：
     $$u(n)=\{\begin{array}{ll}1,& n\ge 0\\ 0,& n<0\end{array}$$
   • 意义：它表示一个信号从某个时刻开始出现并保持不变。
   • 应用：常用来表示信号的开始或开关动作，很多因果序列（即只在 $n\ge 0$ 有值的序列）都会乘以 $u(n)$。

3. 矩形序列 (Rectangular Sequence)

   • 定义：
     $$R_M(n)=\{\begin{array}{ll}1,& 0\le n\le M-1\\ 0,& \text{其他}\end{array}$$
   • 意义：在一段有限的时间内（长度为 $M$）取值为1，其他时间为0。
   • 应用：常用于模拟数据帧、有限持续时间内的信号片段。

4. 实指数序列 (Real Exponential Sequence)

   • 定义：$x(n)=a^{n}u(n)$
   • 意义：如果 $|a|>1$，序列会指数增长；如果 $|a|<1$，序列会指数衰减。
   • 应用：在物理、工程中模拟各种衰减或增长过程。

5. 正弦序列 (Sinusoidal Sequence)

   • 定义：$x(n)=A\cos ({\omega }_{0}n+\varphi )$
   • 意义：离散时间下的周期性振荡信号。
   • 参数：$A$ 为幅度，${\omega }_0$ 为数字角频率（单位：弧度/样本），$\varphi$ 为初始相位。
   • 重要提示： 与模拟正弦信号不同，数字正弦序列不一定都是周期的！这是一个非常重要的特性。

6. 复指数序列 (Complex Exponential Sequence)

   • 定义：$x(n)=e^{j{\omega }_{0}n}=\cos ({\omega }_{0}n)+j\sin ({\omega }_{0}n)$
   • 意义：它是正弦序列的更通用形式，是傅里叶分析和Z变换的基石。任何一个离散时间信号都可以被分解成复指数序列的叠加。
   • 应用：理论分析和频率域变换的核心。

序列的周期性：数字信号的“循环”

对于一个序列 $x(n)$，如果存在一个最小的正整数 $N_0$，使得 $x(n)=x(n+N_0)$ 对所有 $n$ 都成立，那么称 $x(n)$ 是周期序列，$N_0$ 称为最小正周期或基波周期。

判断正弦序列 $x(n)=A\cos ({\omega }_{0}n+\varphi )$ 或复指数序列 $x(n)=e^{j{\omega }_{0}n}$ 的周期性：
序列要具有周期性，需要满足 ${\omega }_0{N}_0=2\pi k$，其中 $k$ 是一个整数。
这意味着 ${\omega }_0/(2\pi )=k/N_0$。
因此，数字角频率 ${\omega }_0$ 必须是 $2\pi$ 的有理数倍，序列才是周期的。
如果 ${\omega }_0/(2\pi )$ 是一个有理数 $k/N$（其中 $k$ 和 $N$ 是互质的整数），那么最小正周期就是 $N_0=N$。

举个例子：

• 序列 $x(n)=\cos (\frac{3\pi }{8}n)$
  这里的 ${\omega }_0=\frac{3\pi }{8}$。
  $\frac{{\omega }_0}{2\pi }=\frac{3\pi /8}{2\pi }=\frac{3}{16}$。
  这是一个有理数。$k=3,N=16$。由于 $3$ 和 $16$ 互质，所以最小正周期 $N_0=16$。这个序列是周期的。
• 序列 $x(n)=\sin (0.3n)$
  这里的 ${\omega }_0=0.3$。
  $\frac{{\omega }_0}{2\pi }=\frac{0.3}{2\pi }=\frac{3}{20\pi }$。
  这是一个无理数（因为含有 $\pi$）。所以这个序列不是周期的。

序列的基本运算：数字信号的“积木”

对序列进行运算是数字信号处理的基础，就像用积木搭建模型一样。

1. 加法与乘法：

   • 逐点运算，非常直观。
   • $y(n)=x_1(n)+x_2(n)$
   • $y(n)=x_1(n)\cdot x_2(n)$

2. 时移 (Time Shift)：

   • 将序列在时间轴上向左或向右移动。
   • $y(n)=x(n-n_0)$
   • 如果 $n_0>0$，表示将 $x(n)$ 向右（延迟）移动 $n_0$ 个单位。
   • 如果 $n_0<0$，表示将 $x(n)$ 向左（超前）移动 $|n_0|$ 个单位。
   • 应用：模拟信号的延迟、控制系统中状态的滞后等。

3. 翻转 (Folding/Reversal)：

   • 将序列沿 $n=0$ 轴进行镜像翻转。
   • $y(n)=x(-n)$

4. 累加 (Accumulation)：

   • 将序列从负无穷到当前点的值进行求和。
   • $y(n)={\sum }_{m=-\infty }^{n}x(m)$
   • 意义：是模拟信号积分的离散对应。例如，对速度序列进行累加可以得到位移序列。

5. 差分 (Differencing)：

   • 计算序列相邻两个点之间的差值。
   • $y(n)=x(n)-x(n-1)$
   • 意义：是模拟信号微分的离散对应。例如，对位移序列进行差分可以得到速度序列。

6. 尺度变换 (Scaling)：

   • 改变序列的“时间”尺度。
   • $y(n)=x(an)$
   • 重要限制： 只有当 $an$ 为整数时，这个操作才有意义。这意味着，你不能随便“拉伸”或“压缩”一个离散序列，你只能在某些特定的点上“采样”或者“插值”。例如，$x(2n)$ 表示每隔一个点取一个值，这相当于对原始信号进行“抽取”；而 $x(n/2)$ 则需要考虑插值。

7. 能量 (Energy)：

   • 有限能量信号的能量定义为：
     $$E_x=\sum _{n=-\infty }^{\infty }|x(n){|}^2$$
   • 功率 (Power)：对周期信号或能量无限的信号，通常定义为平均功率。
     $$P_x=\underset{N\to \infty }{\lim }\frac{1}{2N+1}\sum _{n=-N}^N|x(n){|}^2$$
   • 意义：衡量信号的“强度”或“大小”。

这些基本概念和运算，是理解后续更复杂DSP内容的基础。请务必熟练掌握。

信号的“处理器”：离散时间系统

有了离散时间信号这个“原料”，我们还需要“加工厂”来处理它们。这个“加工厂”就是离散时间系统。

什么是离散时间系统？

一个离散时间系统可以看作是一个黑箱子，它接收一个输入序列 $x(n)$，经过一系列处理，产生一个输出序列 $y(n)$。我们可以用 $T[\cdot ]$ 来表示这个系统，即 $y(n)=T[x(n)]$。

系统通常通过差分方程来描述，例如：$y(n)=0.5x(n)+0.5x(n-1)$，表示当前输出是当前输入和前一个输入的平均值。

系统的基本特性：数字系统的高效运行法则

在众多系统特性中，线性和时不变性是最重要的两个。如果一个系统同时满足这两者，我们称之为线性时不变系统 (LTI System)，它在DSP中具有无与伦比的地位。

1. 线性 (Linearity)：
   线性系统满足叠加原理。这意味着：

   • 齐次性（Homogeneity）： 对输入信号进行放大，输出信号也会按相同的比例放大。
     $T[ax(n)]=aT[x(n)]$
   • 可加性（Additivity）： 多个输入信号之和的输出，等于每个信号单独输入时的输出之和。
     $T[x_1(n)+x_2(n)]=T[x_1(n)]+T[x_2(n)]$
   • 更简洁的验证方式是同时验证：$T[a{x}_1(n)+b{x}_2(n)]=aT[x_1(n)]+bT[x_2(n)]$。
   • 直观理解： 线性系统不会对信号产生“变形扭曲”，它处理信号的方式是“公平”的，不偏不倚。例如，一个音响系统，你把音量调大一倍，声音的“形状”不会变，只是响度大了。但如果你把音量调得太大，导致失真（削波），那它就变得非线性了。

2. 时不变性 (Time-Invariance)：
   时不变系统是指，系统的行为不随时间的变化而改变。

   • 如果输入 $x(n)$ 产生输出 $y(n)$，那么将输入延迟 $n_0$ 个单位时间，即 $x(n-n_0)$，产生的输出也仅仅是 $y(n)$ 延迟 $n_0$ 个单位时间，即 $y(n-n_0)$。
     $T[x(n-n_0)]=y(n-n_0)$
   • 直观理解： 一个时不变的信号处理算法，今天用它处理一段语音，明天用它处理同一段语音，结果应该完全一样。例如，一个数字滤波器，它的滤波效果不会因为你是在上午用还是下午用而改变。但如果你家里的老式收音机，随着电池电量下降，信号接收效果变差，那它就是一个时变系统。

LTI 系统：数字信号处理的“黄金标准”

由于线性系统和时不变系统具有优秀的数学性质，所以DSP中绝大部分理论和算法都是围绕LTI系统展开的。LTI系统的核心在于，它的行为完全由其单位脉冲响应 $h(n)$ 来决定。

卷积：LTI 系统的“核心算法”

一个LTI系统最重要的特性是，它的输出 $y(n)$ 可以通过输入 $x(n)$ 与其单位脉冲响应 $h(n)$ 的**卷积（Convolution）**来计算。

• 定义：
  $$y(n)=x(n)\ast h(n)=\sum _{k=-\infty }^{\infty }x(k)h(n-k)$$
  这个公式也称为卷积和。

• 直观理解：
  想象 $x(n)$ 是一系列“刺激”，而 $h(n)$ 是系统对一个“瞬时刺激”（单位脉冲）的“反应模式”。卷积运算的意义是：将输入信号 $x(n)$ 拆解成无数个不同时刻的单位脉冲信号的加权和（每个 $x(k)\delta (n-k)$），然后计算系统对每个单位脉冲的响应（即 $x(k)h(n-k)$），最后将所有这些响应叠加起来，就得到了总的输出 $y(n)$。
  这个过程就像你往一个水池里扔石头，每个石头（$x(k)$）会激起一个涟漪（$h(n-k)$），而最终的水面波动（$y(n)$）是所有涟漪叠加的结果。

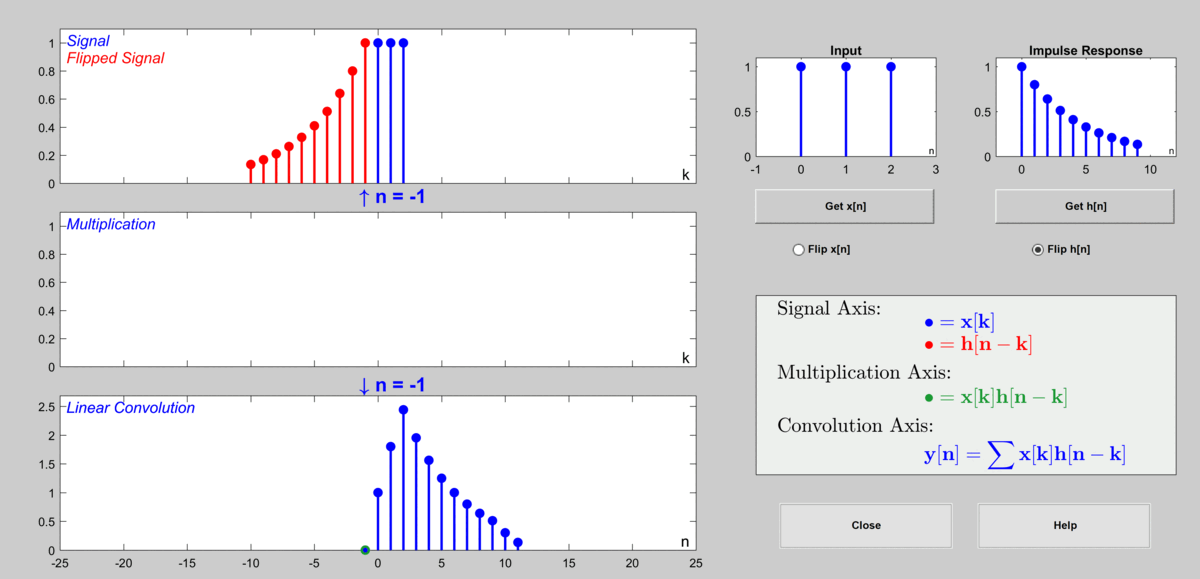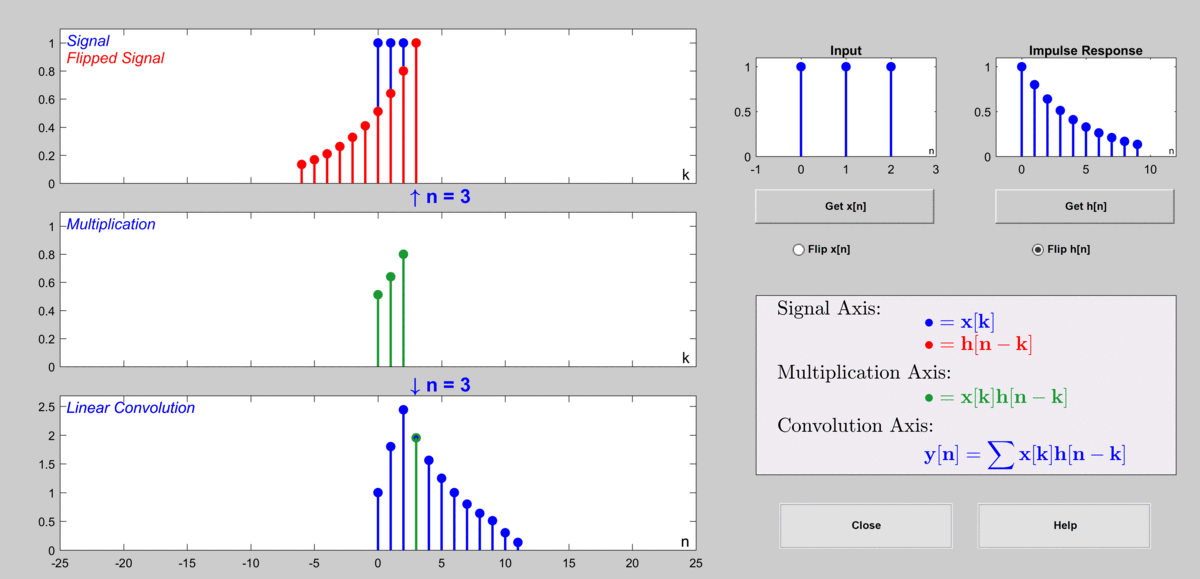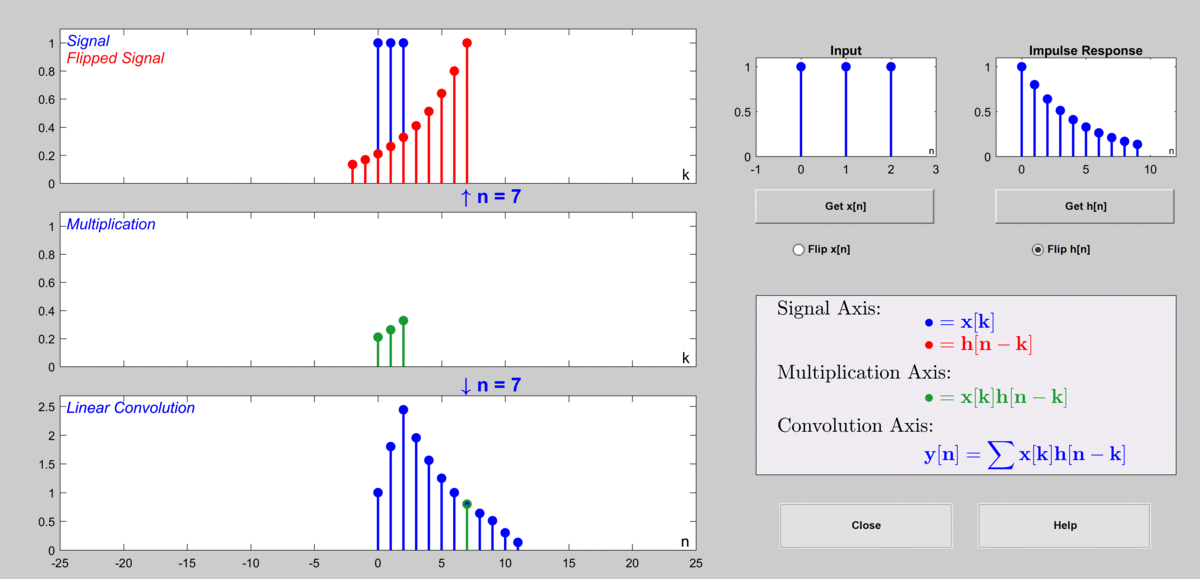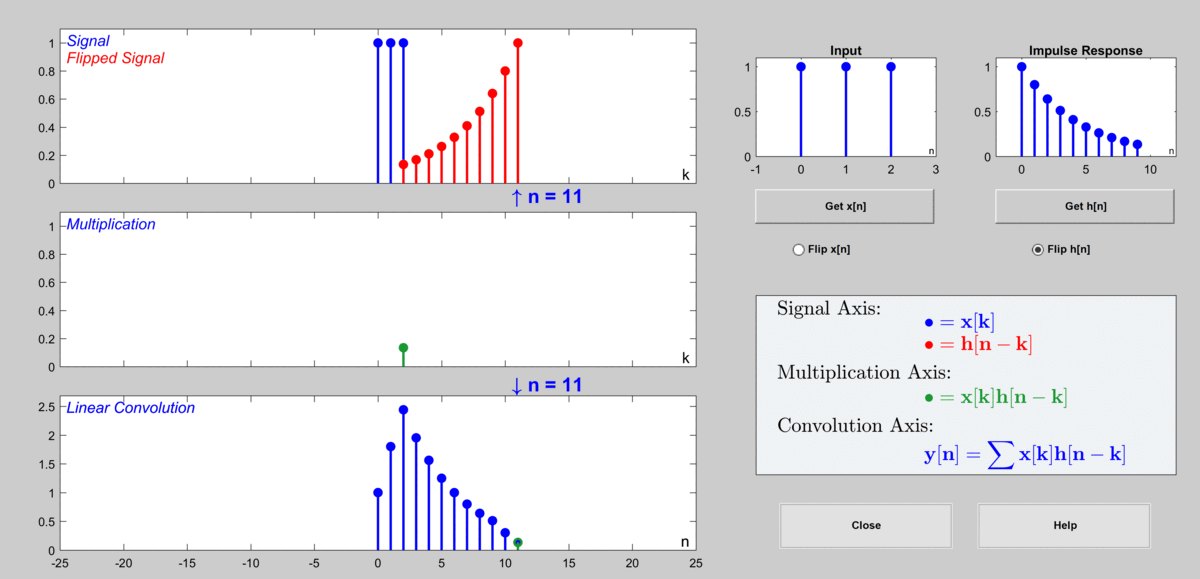
• 卷积性质：
  卷积运算具有一些重要的性质，它们使得复杂系统的分析和设计变得更加容易：
  • 交换律： $x(n)\ast h(n)=h(n)\ast x(n)$
    这表明输入和系统响应的顺序可以互换，结果不变。
  • 结合律： $(x(n)\ast h_1(n))\ast h_2(n)=x(n)\ast (h_1(n)\ast h_2(n))$
    多个LTI系统串联时，它们的整体响应是各个系统响应的卷积。这意味着你可以在分析时先将串联的系统合并为一个等效系统。
  • 分配律： $x(n)\ast (h_1(n)+h_2(n))=x(n)\ast h_1(n)+x(n)\ast h_2(n)$
    多个LTI系统并联时，它们的总输出是各自输出的叠加。

系统的因果性与稳定性：确保系统“可靠”运行

除了线性和时不变性，因果性和稳定性也是衡量系统好坏的重要指标。

1. 因果性 (Causality)：

   • 一个因果系统，其当前时刻的输出 $y(n)$ 只取决于当前时刻和过去时刻的输入 $x(k)$ 以及过去的输出 $y(k)$。它不能“预知未来”。
   • 对于LTI系统： 因果性的要求是其单位脉冲响应 $h(n)$ 必须满足 $h(n)=0$ 对于 $n<0$。
   • 实际意义： 任何能够实时工作的物理系统都必须是因果的。你不能让一个控制器根据传感器未来的读数来决定现在的动作。

2. 稳定性 (Stability)：

   • 我们最常讨论的是BIBO稳定性 (Bounded Input Bounded Output Stability)。一个BIBO稳定的系统，对于任何有界的输入（输入信号的幅度不发散），其输出信号的幅度也必须是有界的（输出信号的幅度也不发散）。
   • 对于LTI系统： BIBO稳定性的条件是其单位脉冲响应 $h(n)$ 必须是绝对可和的，即：
     $$\sum _{n=-\infty }^{\infty }|h(n)|<\infty$$
   • 实际意义： 稳定的系统不会“发散”或“崩溃”。例如，一个控制系统如果不稳定，可能会导致设备振荡加剧，甚至损坏。

差分方程：描述数字系统的“数学语言”

在DSP中，我们通常用线性常系数差分方程 (LCCDE) 来描述LTI系统。这就像在模拟信号处理中用线性常系数微分方程描述系统一样。

线性常系数差分方程的形式

一个典型的N阶LCCDE的形式如下：
$$\sum _{k=0}^N{a}_{k}y(n-k)=\sum _{m=0}^M{b}_{m}x(n-m)$$
其中：

• $y(n)$ 是当前时刻的输出。
• $y(n-k)$ 是过去的输出项。
• $x(n)$ 是当前时刻的输入。
• $x(n-m)$ 是过去的输入项。
• $a_k$ 和 $b_m$ 是常数系数。
• $N$ 是输出项的最大延迟，称为系统的阶数。

例子：
$y(n)-0.5y(n-1)=x(n)+0.2x(n-1)$
这是一个1阶LCCDE。

求解方法

1. 递推解法 (Iterative Solution)：
   当给定输入序列 $x(n)$ 和系统的初始条件（即 $y(-1),y(-2),\dots$）时，我们可以通过将差分方程改写为递推形式来逐步计算输出 $y(n)$。
   例如，对于上面的方程，可以改写为：$y(n)=0.5y(n-1)+x(n)+0.2x(n-1)$。
   这样，你就可以从 $n=0$ 开始，依次计算 $y(0),y(1),y(2),\dots$。

   求解单位脉冲响应 $h(n)$：
   递推法的一个重要应用就是求解系统的单位脉冲响应 $h(n)$。根据定义，$h(n)$ 是当输入 $x(n)=\delta (n)$ 且所有初始条件为零时系统的输出。
   步骤：

   1. 令 $x(n)=\delta (n)$。
   2. 设定所有初始条件为零（即 $y(n)=0$ for $n<0$）。
   3. 从 $n=0$ 开始，逐点递推计算 $y(n)$ 的值。

   例： 求 $y(n)-0.5y(n-1)=x(n)$ 的单位脉冲响应 $h(n)$。
   改写为 $y(n)=0.5y(n-1)+x(n)$。
   令 $y(-1)=0$。

   • $n=0$ 时：$h(0)=0.5h(-1)+\delta (0)=0.5\times 0+1=1$
   • $n=1$ 时：$h(1)=0.5h(0)+\delta (1)=0.5\times 1+0=0.5$
   • $n=2$ 时：$h(2)=0.5h(1)+\delta (2)=0.5\times 0.5+0=0.25$
   • $n=3$ 时：$h(3)=0.5h(2)+\delta (3)=0.5\times 0.25+0=0.125$
     依此类推，得到 $h(n)=(0.5{)}^{n}u(n)$。

2. 经典解法 (齐次解 + 特解)：
   与微分方程类似，解差分方程也可以分为求解齐次方程的解（系统的自由响应）和特解（系统的受迫响应），然后叠加。这种方法在手算时比较复杂，不如 Z 变换法常用。

3. 变换域解法 (Z 变换)：
   这是最强大、最常用的方法。通过将差分方程转换为Z域的代数方程来求解，大大简化了计算。我们将在第二章详细介绍。

从模拟到数字：信号的“数字化之旅”

现在我们已经了解了离散时间信号和系统本身，但现实世界中的信号往往是模拟的。如何将这些模拟信号“送入”数字系统进行处理呢？这就涉及到了模数转换 (A/D Conversion) 和 数模转换 (D/A Conversion)。

A/D 转换：现实世界的“扫描仪”

A/D 转换器（ADC）是连接模拟世界和数字世界的桥梁。它将连续时间的模拟信号 $x_a(t)$ 转换为离散时间的数字信号 $x(n)$。这个过程通常包含三个关键步骤：

1. 采样 (Sampling)：
   这是模数转换的第一步，也是最重要的一步。它以固定的时间间隔 $T$（采样周期）对模拟信号的幅度进行测量。
   如果采样频率为 $f_s=1/T$，那么采样序列就是 $x(n)=x_a(nT)$。

   采样定理 (Nyquist-Shannon Sampling Theorem)：
   这是DSP中的“黄金法则”！它告诉我们，为了能够从采样序列中无失真地恢复原始模拟信号，采样频率 $f_s$ 必须至少是模拟信号中最高频率 $f_c$ 的两倍。
   即：$f_s\ge 2f_c$

   如果采样频率低于 $2f_c$，就会发生混叠 (Aliasing) 现象。混叠是指高频分量被错误地映射到低频区域，导致信号失真，且这种失真无法通过后续处理消除。
   例如，你用摄像机拍摄一个高速旋转的车轮，如果帧率（采样频率）不够高，车轮可能看起来在缓慢地向后转动，这就是一种视觉上的混叠。

   在数字域，频率 $\omega$ 与模拟域频率 $\Omega$ 的关系是 $\omega =\Omega T=\Omega /f_s$。
   根据采样定理，最高模拟频率 $f_c$ 对应数字频率 ${\omega }_c=2\pi f_c/f_s\le \pi$。
   因此，数字频率通常位于范围 $[-\pi ,\pi )$ 或 $[0,2\pi )$ 之间。
   

2. 量化 (Quantization)：
   采样的结果仍然是连续的幅度值（虽然时间是离散的）。量化是将这些连续的幅度值转换为有限的、离散的幅度值。
   例如，一个声音信号的采样值可能是 0.325V，如果用8位量化，它可能被量化为 0.32V。这个过程会引入量化误差或量化噪声。量化位数越多，量化误差越小，但所需的存储空间和计算资源也越多。

3. 编码 (Coding)：
   量化后的离散幅度值需要被转换为二进制代码，以便数字电路和计算机进行存储和处理。这是从“离散值”到“数字代码”的最终步骤。

D/A 转换：数字信号的“复原师”

D/A 转换器（DAC）是模数转换的逆过程，它将数字信号 $x(n)$ 转换为模拟信号 $y_a(t)$。

1. 数字到模拟的转换： DAC 接收二进制代码，并将其转换为对应的模拟幅度值（通常是电压或电流）。
2. 重建滤波器 (Reconstruction Filter)：
   DAC 输出的模拟信号通常是一个“阶梯状”的信号，它由一系列在采样点上跳变的离散电平组成。为了得到平滑的、接近原始的模拟信号，我们需要使用一个重建滤波器，通常是一个低通滤波器。
   这个滤波器会滤除数字信号中采样带来的高频成分（例如，零阶保持器输出的“台阶”之间的矩形脉冲），从而“平滑”信号，使其恢复到接近原始模拟信号的形态。

在实际应用中，模数转换和数模转换的质量直接影响着数字信号处理系统的性能。优秀的ADC和DAC是高性能DSP系统的基础。

---

总结与展望

在这一章中，我们踏入了数字信号处理的大门，认识了最基本的“砖块”和“工具”：

• 离散时间信号（序列）：理解它们如何表示，常见的类型有哪些，以及它们的基本运算和周期性。
• 离散时间系统：学习了系统的基本属性——线性、时不变性、因果性和稳定性。其中，LTI系统因其特性优良而成为DSP的焦点，而卷积则是描述LTI系统核心行为的数学工具。
• 线性常系数差分方程：这是描述LTI系统的数学语言，我们了解了其形式及基本的递推求解方法。
• 模数/数模转换：理解了信号从模拟世界进入数字世界（采样、量化、编码）和从数字世界返回模拟世界（DAC、重建滤波）的关键过程，以及采样定理的重要性。

这些知识点就像是DSP大厦的地基。虽然现在你可能觉得有些概念还比较抽象，但请相信，随着我们学习的深入，你会越来越体会到它们的重要性。下一章，我们将介绍一种更强大的数学工具——Z变换，它能将时域的卷积运算转化为Z域的简单乘法，极大地简化LTI系统的分析和设计。敬请期待！

---

习题

学以致用，下面是几道练习题，帮助你巩固本章的知识点。

1. 序列周期性判断：
判断以下序列是否是周期的，如果是，请计算其最小正周期 $N_0$。
a) $x(n)=\cos (\frac{3\pi }{8}n)$
b) $x(n)=\sin (0.3n)$
c) $x(n)=e^{j\frac{2\pi }{5}n}+e^{j\frac{4\pi }{7}n}$

2. 系统特性判断 (线性与时不变性)：
判断以下系统是否是线性的，是否是时不变的。给出你的判断依据。
a) $y(n)=x(n^2)$
b) $y(n)=x(n)+x(n-1)$
c) $y(n)=x(n)+n$

3. 卷积运算：
已知序列 x ( n ) = { 1 , 2 , 3 } x(n) = \{1, 2, 3\} x(n)={1,2,3} (从 $n=0$ 开始) 和 h ( n ) = { 1 , 1 } h(n) = \{1, 1\} h(n)={1,1} (从 $n=0$ 开始)。计算 $y(n)=x(n)\ast h(n)$。
提示：可以使用卷积和的定义 $y(n)={\sum }_{k=-\infty }^{\infty }x(k)h(n-k)$。

4. 递推法求解差分方程和单位脉冲响应：
一个因果 LTI 系统由差分方程描述：$y(n)-0.5y(n-1)=x(n)$。
a) 用递推法计算当输入 $x(n)=\delta (n)$ 且初始条件为零时的输出 $y(n)$，即系统的单位脉冲响应 $h(n)$ 的前5个值 ($h(0)$ 到 $h(4)$)。
b) 判断该系统是否稳定，是否因果。

---

答案

1. 序列周期性判断：
a) 对于 $x(n)=\cos (\frac{3\pi }{8}n)$，数字角频率 ${\omega }_0=\frac{3\pi }{8}$。
$\frac{{\omega }_0}{2\pi }=\frac{3\pi /8}{2\pi }=\frac{3}{16}$。这是一个有理数。因为 $k=3,N=16$ 且 $\text{gcd}(3,16)=1$，所以序列是周期的，最小正周期 $N_0=16$。
b) 对于 $x(n)=\sin (0.3n)$，数字角频率 ${\omega }_0=0.3$。
$\frac{{\omega }_0}{2\pi }=\frac{0.3}{2\pi }=\frac{3}{20\pi }$。这是一个无理数（含有 $\pi$），所以序列不是周期的。
c) 对于 $x(n)=e^{j\frac{2\pi }{5}n}+e^{j\frac{4\pi }{7}n}$，这是一个复合序列。
第一个分量 $x_1(n)=e^{j\frac{2\pi }{5}n}$ 的周期 $N_1=5$ (因为 $\frac{2\pi /5}{2\pi }=\frac{1}{5}$)。
第二个分量 $x_2(n)=e^{j\frac{4\pi }{7}n}$ 的周期 $N_2=7$ (因为 $\frac{4\pi /7}{2\pi }=\frac{2}{7}$，$\text{gcd}(2,7)=1$，$N_2=7$)。
复合序列的周期是两个分量周期的最小公倍数：$N_0=\text{lcm}(N_1,N_2)=\text{lcm}(5,7)=35$。
所以序列是周期的，最小正周期 $N_0=35$。

2. 系统特性判断 (线性与时不变性)：
a) $y(n)=x(n^2)$

• 线性： 设 $x(n)=a{x}_1(n)+b{x}_2(n)$。
  $y(n)=T[a{x}_1(n)+b{x}_2(n)]=(a{x}_1(n)+b{x}_2(n^2))=a{x}_1(n^2)+b{x}_2(n^2)=aT[x_1(n)]+bT[x_2(n)]$。
  所以是线性的。
• 时不变性： 设 $y(n)=x(n^2)$。
  延迟输入：$x^{\prime }(n)=x(n-n_0)$。则 $y^{\prime }(n)=T[x(n-n_0)]=x((n-n_0{)}^2)$。
  延迟输出：$y(n-n_0)=x((n-n_0{)}^2)$。
  这两个不相等，例如，当 $n_0=1$， $y(n-1)=x((n-1{)}^2)$，而 $y^{\prime }(n)=x(n^2-2n_0+n_0^2)$ 不等于 $x((n-n_0{)}^2)$。
  举例：$x(n)=\delta (n)$, $y(n)=\delta (n^2)=\delta (n)$。
  $x(n-1)=\delta (n-1)$, $y^{\prime }(n)=\delta ((n-1{)}^2)$ 只在 $n=1$ 有值。
  $y(n-1)=\delta (n-1)$。
  显然 $y^{\prime }(n)\ne y(n-1)$。所以是时变的。
  结论：线性，时变。

b) $y(n)=x(n)+x(n-1)$

• 线性： 设 $x(n)=a{x}_1(n)+b{x}_2(n)$。
  $y(n)=(a{x}_1(n)+b{x}_2(n))+(a{x}_1(n-1)+b{x}_2(n-1))$
  $y(n)=a(x_1(n)+x_1(n-1))+b(x_2(n)+x_2(n-1))$
  $y(n)=aT[x_1(n)]+bT[x_2(n)]$。
  所以是线性的。
• 时不变性： 设 $y(n)=x(n)+x(n-1)$。
  延迟输入：$x^{\prime }(n)=x(n-n_0)$。则 $y^{\prime }(n)=T[x(n-n_0)]=x(n-n_0)+x(n-n_0-1)$。
  延迟输出：$y(n-n_0)=x(n-n_0)+x(n-n_0-1)$。
  $y^{\prime }(n)=y(n-n_0)$。所以是时不变的。
  结论：线性，时不变。

c) $y(n)=x(n)+n$

• 线性： 设 $x(n)=a{x}_1(n)+b{x}_2(n)$。
  $y(n)=(a{x}_1(n)+b{x}_2(n))+n$。
  而 $aT[x_1(n)]+bT[x_2(n)]=a(x_1(n)+n)+b(x_2(n)+n)=a{x}_1(n)+b{x}_2(n)+(a+b)n$。
  由于 $n$ 项的存在，如果 $a+b\ne 1$，则不满足线性。例如，取 $a=1,b=1$，则 $y(n)=x_1(n)+x_2(n)+n$，而 $T[x_1(n)]+T[x_2(n)]=x_1(n)+n+x_2(n)+n=x_1(n)+x_2(n)+2n$。所以不满足线性。
• 时不变性： 设 $y(n)=x(n)+n$。
  延迟输入：$x^{\prime }(n)=x(n-n_0)$。则 $y^{\prime }(n)=T[x(n-n_0)]=x(n-n_0)+n$。
  延迟输出：$y(n-n_0)=x(n-n_0)+(n-n_0)$。
  由于 $n$ 项变为 $n-n_0$，所以 $y^{\prime }(n)\ne y(n-n_0)$。所以是时变的。
  结论：非线性，时变。

3. 卷积运算：
x ( n ) = { 1 , 2 , 3 } x(n) = \{1, 2, 3\} x(n)={1,2,3} (从 $n=0$ 开始)，即 $x(0)=1,x(1)=2,x(2)=3$。
h ( n ) = { 1 , 1 } h(n) = \{1, 1\} h(n)={1,1} (从 $n=0$ 开始)，即 $h(0)=1,h(1)=1$。
卷积长度 $L=(3-1)+(2-1)+1=2+1+1=4$。
$y(n)={\sum }_{k=-\infty }^{\infty }x(k)h(n-k)$

• $y(0)=x(0)h(0)=1\cdot 1=1$
• $y(1)=x(0)h(1)+x(1)h(0)=1\cdot 1+2\cdot 1=3$
• $y(2)=x(0)h(2)+x(1)h(1)+x(2)h(0)=1\cdot 0+2\cdot 1+3\cdot 1=5$
• $y(3)=x(1)h(2)+x(2)h(1)=2\cdot 0+3\cdot 1=3$
• 对于其他 $n$ 值，$y(n)=0$。
  所以， y ( n ) = { 1 , 3 , 5 , 3 } y(n) = \{1, 3, 5, 3\} y(n)={1,3,5,3} (从 $n=0$ 开始)。

4. 递推法求解差分方程和单位脉冲响应：
差分方程：$y(n)-0.5y(n-1)=x(n)$
a) 求单位脉冲响应 $h(n)$：令 $x(n)=\delta (n)$，且初始条件为零（即 $y(-1)=0$）。
将方程改写为递推形式：$y(n)=0.5y(n-1)+x(n)$。

• $n=0$ 时：$h(0)=0.5h(-1)+\delta (0)=0.5\cdot 0+1=1$
• $n=1$ 时：$h(1)=0.5h(0)+\delta (1)=0.5\cdot 1+0=0.5$
• $n=2$ 时：$h(2)=0.5h(1)+\delta (2)=0.5\cdot 0.5+0=0.25$
• $n=3$ 时：$h(3)=0.5h(2)+\delta (3)=0.5\cdot 0.25+0=0.125$
• $n=4$ 时：$h(4)=0.5h(3)+\delta (4)=0.5\cdot 0.125+0=0.0625$
  所以，$h(0)=1,h(1)=0.5,h(2)=0.25,h(3)=0.125,h(4)=0.0625$。
  (事实上，$h(n)=(0.5{)}^{n}u(n)$)

b) 判断该系统是否稳定，是否因果。

• 因果性： 从 $h(n)=(0.5{)}^{n}u(n)$ 可以看出，当 $n<0$ 时，$h(n)=0$。所以系统是因果的。
  (根据差分方程，当前输出 $y(n)$ 只依赖于当前输入 $x(n)$ 和过去的输出 $y(n-1)$，因此也是因果的。)
• 稳定性： 检查单位脉冲响应是否绝对可和：
  ${\sum }_{n=-\infty }^{\infty }|h(n)|={\sum }_{n=0}^{\infty }|(0.5{)}^n|={\sum }_{n=0}^{\infty }(0.5{)}^n$
  这是一个几何级数求和，当公比 $|0.5|<1$ 时，和为 $\frac{1}{1-0.5}=\frac{1}{0.5}=2$。
  因为 ${\sum }_{n=-\infty }^{\infty }|h(n)|=2<\infty$，所以系统是稳定的。

结论：稳定且因果。