KungfuBot——基于物理约束和自适应运动追踪的人形全身控制PBHC，用于学习打拳或跳舞(即RL下的动作模仿和运控)

前言

昨天618，我司「七月在线」同事朝阳为主力，我打杂，折腾了整整一天，终于可以通过VR摇操宇树G1了——当然，摇操是为了做训练数据的采集，从而方便下一步的模型(策略)训练，最终实现机器人自主做各种任务

然灵巧手还没到货(顺带吐槽一下，现在的灵巧手都太贵了，有没有性价比高的或者合作呢，如有，欢迎私我)，临时再打印个二指夹爪也得等

那未来这几天搞啥呢？那就搞运动吧，如此，便关注到最新出来的两个工作

一个是GMT: General Motion Tracking forHumanoid Whole-Body Control
另一个则是本文要解读的KungfuBot

顺带和后者KungfuBot的一位作者沟通发现，一者他们团队同学也读过我的博客，二者他导师还是我认识多年的朋友，也是缘分啊

加之他们开源的力度我个人觉得挺不错的，故我也打算和长沙具身团队其中的一个人形小组复现下该KungfuBot
故写本文一方面算是对复现的指导，二方面也是对他们工作的一个宣传，一举多得何乐不为

PS，如有具身某业务场景的定制开发需求，可以直接私我需求，如想做技术交流则私我一两句简介，邀你进：七月具身：人形二开交流大群

第一部分 KungfuBot

1.1 引言与相关工作

1.1.1 引言

如原KungfuBot论文所说，人形机器人由于具有人类般的形态结构，具备模仿人类在执行不同任务时各种行为的潜力[1-Humanoid locomotion and manipulation: Current progress and challenges in control, planning, and learning]

随着动作捕捉（Mo-Cap）系统和动作生成方法的不断进步，已经产生了大量的动作数据集
2- Motiongpt: Human motion as a foreign language
3-Move as you say interact as you can: Language-guided human motion generation with scene affordance
这些数据集涵盖了大量带有文本描述的人类活动[4-Amass: Archive of motion capture as surface shapes]

因此，使人形机器人学习全身控制以模仿人类行为成为了一个有前景的方向
然而，控制高维度的机器人动作以实现理想的人类表现仍然面临巨大挑战。主要困难之一在于，从人类采集的动作序列往往不符合仿人机器人的物理约束，包括关节极限、动力学和运动学
5-Exbody2
6-ASAP

因此，直接通过强化学习（RL）训练策略以最大化奖励（如负跟踪误差）通常难以获得理想的策略，因为理想解可能并不存在于解空间中
近期，已经提出了多种基于强化学习（RL）的全身控制框架用于动作跟踪
7-Exbody
8-Humanplus
这些方法通常将参考运动学动作作为输入，并输出用于类人机器人模仿的控制动作

为了解决物理可行性问题，H2O和 OmniH2O [9,10] 通过训练有特权的模仿策略去除不可行的动作，从而生成干净的动作序列数据集

ExBody [7] 通过语言标签（如“挥手”和“行走”）筛选，构建了一个可行的动作数据集。Exbody2 [5] 在所有动作上训练初始策略，并利用跟踪误差来衡量每个动作的难度。然而，训练初始策略并寻找最优数据集的成本较高

此外，在训练过程中，对于难以跟踪的动作，仍缺乏合适的容错机制。因此，先前的方法只能跟踪低速且平滑的动作
最近，ASAP [6] 引入了多阶段机制，并学习了残差策略来补偿仿真到现实的差异，从而降低了跟踪敏捷动作的难度。然而，ASAP 包含总共四个训练阶段，并且残差策略的训练需要 MoCap 系统记录真实机器人状态

在本文中，来自1 中国电信(TeleAI)、2 上交、3 华东理工大学、4 哈工大、5 上科大的研究者提出了一种基于物理的人形机器人运动控制方法（PBHC）

其对应的论文为：KungfuBot: Physics-Based Humanoid Whole-Body Control for Learning Highly-Dynamic Skills
其对应的作者为——本文中凡是出现的“作者”或“他们”一词，均代表他们：
Weiji Xie* 1,2、Jinrui Han* 1,2、Jiakun Zheng* 1,3、Huanyu Li1,4、Xinzhe Liu1,5
Jiyuan Shi1、Weinan Zhang2、Chenjia Bai† 1、Xuelong Li† 1
其对应的项目地址为：https://kungfu-bot.github.io/
其对应的GitHub为：TeleHuman/PBHC

具体而言，该方法采用两阶段框架来应对敏捷且高度动态运动所带来的挑战

在运动处理阶段
首先从视频中提取运动数据，并通过在人体模型内估算物理量来建立基于物理的指标，从而筛选出人类动作，剔除超出物理极限的运动
随后，计算运动的接触掩码，进行运动修正，并最终利用微分逆运动学将处理后的动作重定向到机器人上
在运动模仿阶段，作者提出了一种自适应运动跟踪机制，通过跟踪因子调整跟踪奖励。由于参考动作存在不完善以及需要实现平滑控制，完全跟踪高难度动作在实际中不可行，因此作者根据跟踪误差对不同动作自适应调整跟踪因子

随后，作者又提出了一个双层优化(Bi-Level Optimization，BLO)[11- An introduction to bilevel optimization: Foundations and applications in signal processing and machine learning]来求解最优因子，并设计了自适应更新规则，在训练过程中在线估算跟踪误差，以动态优化跟踪因子

此外，作者在两阶段框架的基础上，设计了一种非对称的actor-critic结构用于策略优化。Critic采用奖励向量化技术，并利用特权信息提升价值估计的准确性，而actor仅依赖本地观测

1.1.2 相关工作

首先，对于人形动作模仿

机器人动作模仿旨在从人类动作中学习逼真且自然的行为[21,23]。尽管已有多个包含多样动作的数据集[24,25,4]，但由于人类与类人机器人在物理结构上存在显著差异[6,26]，类人机器人无法直接学习这些多样化的行为。同时，大多数数据集缺乏物理信息，例如对机器人策略学习至关重要的足部接触标注[27,28]。因此，作者采用基于物理的动作处理方法进行动作筛选和接触标注
在获得参考动作后，类人机器人学习全身控制策略以与仿真器交互[29,30]，目标是获得接近参考动作的状态轨迹[31,32]。然而，学习此类策略极具挑战性，因为机器人需要对高维自由度进行精确控制，以实现稳定且真实的运动[7,8]
近期的研究采用基于物理的动作筛选和强化学习来学习全身控制策略[5,10]，并通过仿真到现实迁移实现真实世界的适应[33]。但由于缺乏对高难度动作的容错机制，这些方法仅能跟踪相对简单的动作
其他研究还结合了遥操作[34,35]以及上下半身的独立控制[36]，但可能牺牲了动作的表现力。相比之下，KungfuBot提出了一种自适应机制，可针对敏捷动作动态调整跟踪奖励

其次，对于仿人机器人全身控制

传统的仿人机器人方法通常分别为行走和操作学习独立的控制策略

在下半身方面，基于强化学习（RL）的控制器已被广泛应用于学习复杂任务的行走策略，如复杂地形行走[37,38]、步态控制[39]、起身[40,41]、跳跃[42]，甚至跑酷[43,44]。然而，每项行走任务都需要精细的奖励设计，并且难以获得类人的行为[45,46]
相比之下，KungfuBot采用人类动作作为参考，这使机器人更容易获得类人的行为
在上半身方面，各种方法提出了不同的架构来学习操作任务，例如扩散策略[47,48]、视觉-语言-动作模型[49,50,51]、双系统架构[52,53]和世界模型[54,55]
然而，这些方法可能忽视了双臂的协调性

近年来，已经提出了若干全身控制方法，旨在增强整个系统在行走[22,39,34]或执行行走-操作任务[56]时的鲁棒性

与之不同的是，KungfuBot的方法使上下半身拥有相同的目标，即跟踪参考动作，同时下半身仍需在动作模仿中保持稳定并防止跌倒。其他方法通过收集全身控制数据集来训练仿人基础模型[56,57]，但需要大量的轨迹
相比之下，KungfuBot只需少量参考动作即可学习多样化的行为

1.1.3 预备知识：问题表述和参考动作处理

首先，对于问题表述

作者在工作中采用了Unitree G1 机器人[12]，该机器人具有23 个自由度（DoFs）可供控制，不包括每只手腕中的3DoFs。且他们将运动模仿问题表述为一个以目标为条件的强化学习问题，其马尔可夫决策过程为 $\mathcal{M}=\left(\mathcal{S}, \mathcal{A}, \mathcal{S}^{\mathrm{ref}}, \gamma, r, P\right)$ ，其中

$\mathcal{S}$ 和 $\mathcal{S}^{\mathrm{ref}}$ 分别表示人形机器人和参考运动的状态空间
$\mathcal{A}$ 为机器人的动作空间
$r$ 是由运动跟踪和正则化奖励组成的混合奖励函数
$P$ 是依赖于机器人形态和物理约束的转移函数

在每个时间步 $t$

策略 $\pi$ 观察机器人本体感知状态 $\boldsymbol{s}_{t}^{\text {prop }}$ 并生成动作 $a_{t}$ ，其目标是获得下一个状态 $\boldsymbol{s}_{t+1}$ ，该状态跟随参考轨迹 $\left[\boldsymbol{s}_{0}^{\text {ref }}, \ldots, \boldsymbol{s}_{N-1}^{\text {ref }}\right]$ 中的对应参考状态 $\boldsymbol{s}_{t+1}^{\mathrm{ref}}$
动作 $\boldsymbol{a}_{t} \in \mathbb{R}^{23}$ 是用于PD 控制器计算电机扭矩的目标关节位置
PD控制器的增益参数列于表9。为提高训练中模拟器的数值稳定性和精度，作者将踝关节连杆的惯性手动设置为固定值 $5 \times 10^{-3}$
且采用了现成的强化学习算法PPO[13]，结合actor-critic架构进行策略优化
详细的PPO超参数如表8所示

其次，对于参考动作处理

对于人体动作处理，Skinned Multi-Person Linear (SMPL) 模型[14] 提供了一个通用的人体动作表示方法，使用三个关键参数：

$\boldsymbol{\beta} \in \mathbb{R}^{10}$ 表示身体形状
$\boldsymbol{\theta} \in \mathbb{R}^{24 \times 3}$ 表示关节的轴-角表示旋转
$\psi \in \mathbb{R}^{3}$ 表示全局平移

这些参数可以通过可微分蒙皮函数 $M(\cdot)$ 映射为一个包含6,890 个顶点的三维网格，形式化表达为 $\mathcal{V}=M(\boldsymbol{\beta}, \boldsymbol{\theta}, \boldsymbol{\psi}) \in \mathbb{R}^{6890 \times 3}$

作者采用人体动作恢复模型从视频中估计SMPL 参数 $(\boldsymbol{\beta}, \boldsymbol{\theta}, \boldsymbol{\psi})$ ，随后进行额外的动作处理

最终得到的SMPL 格式动作通过逆运动学（IK）方法重定向到G1，从而获得用于跟踪的参考动作「The resulting SMPL-format motions are then retargeted toG1 through an Inverse Kinematics (IK) method, yielding the reference motions for tracking purposes」，类似Humanplus论文中的这个图「详见此文《HumanPlus——斯坦福ALOHA团队开源的像人类影子一样的人形机器人：仿真中训小脑HST、真实中训大脑HIT》」

1.2 PBHC的完整方法论

PBHC 的总体流程如图 1 所示『包括三个核心组件：(a) 从视频中提取动作及多步动作处理，(b)基于最优跟踪因子的自适应动作跟踪，(c) 强化学习训练框架及从仿真到现实的部署』

首先，原始的人体视频通过人体运动恢复（HMR）模型处理，生成 SMPL 格式的运动序列
这些序列随后通过基于物理的指标进行筛选，并利用接触掩码进行修正
经过优化的运动数据接着被重定向到 G1 机器人
最后，每条生成的轨迹作为参考动作，用于训练独立的强化学习（RL）策略，随后部署到真实的 G1 机器人上

1.2.1 动作处理流程：从视频中进行运动估计、动作筛选、动作校正、动作重定向(含数据集说明)

作者提出了一种动作处理流程，用于从视频中提取动作以实现人形动作追踪，该流程包括四个步骤：

从单目视频中估算SMPL格式的动作
基于物理的动作滤波
基于接触感知的动作校正
动作重定向

该流程确保了物理上合理的动作能够从视频中转移到人形机器人上，接下来，逐一具体阐述上述流程

第一，从视频中进行运动估计

作者采用 GVHMR [15- World-grounded human motion recovery via gravity-view coordinates] 从单目视频中估算 SMPL 格式的运动。GVHMR 引入了一个与重力方向对齐的重力-视角坐标系，自然地将运动与重力方向对齐，从而消除了仅依赖相机坐标系重建时产生的身体倾斜问题
此外，GVHMR 通过预测足部静止概率，有效减轻了足部滑动伪影，从而提升了运动质量

第二，基于物理的运动筛选

由于HMR 模型在重建过程中存在不准确性以及分布外问题，从视频中提取的运动可能会违反物理和生物力学约束，因此，作者尝试通过基于物理的原则筛选这些运动

以往的研究[16-3d human pose estimation via intuitive physics] 表明，质心（CoM）和压力中心（CoP）之间的接近程度可以指示更高的稳定性，并提出了一种从SMPL 数据中估算CoM 和CoP 坐标的方法
在此基础上，作者计算每一帧中CoM 和CoP 在地面的投影距离，并通过设定阈值来评估稳定性
具体来说，令 $\overline{\boldsymbol{p}}_{t}^{\mathrm{CoM}}=\left(p_{t, x}^{\mathrm{CoM}}, p_{t, y}^{\mathrm{CoM}}\right)$ 和 $\overline{\boldsymbol{p}}_{t}^{\mathrm{CoP}}=\left(p_{t, x}^{\mathrm{CoP}}, p_{t, y}^{\mathrm{CoP}}\right)$ 分别表示第 $t$ 帧中CoM 和CoP在地面的投影坐标， $\Delta d_{t}$ 表示这两个投影之间的距离

作者将一帧的稳定性判据定义为——如下公式1所示
$\Delta d_{t}=\left\|\overline{\boldsymbol{p}}_{t}^{\mathrm{CoM}}-\overline{\boldsymbol{p}}_{t}^{\mathrm{CoP}}\right\|_{2}<\epsilon_{\mathrm{stab}}$

其中， $\epsilon_{\text {stab }}$ 表示稳定性阈值

然后，给定一个N 帧的动作序列，令 $\mathcal{B}=\left[t_{0}, t_{1}, \ldots, t_{K}\right]$ 为满足上述公式(1) 的帧索引递增排序列表，其中 $t_{k} \in[1, N]$

若满足以下两个条件，则认为该动作序列是稳定的：
(i) 边界帧稳定性： $1 \in \mathcal{B}$ 且 $N \in \mathcal{B}$
(ii) 最大不稳定间隔：连续不稳定帧的最大长度必须小于阈值 $\epsilon_{\mathrm{N}}$ ，即 $\max _{k} t_{k+1}-t_{k}<\epsilon_{\mathrm{N}}$ 。基于该标准，明显无法保持动态稳定性的动作将从原始数据集中剔除

第三，基于接触掩码的运动校正

为了更好地捕捉运动数据中的足-地接触，作者通过分析连续帧之间的踝关节位移，基于零速度假设[17- Capturing and inferring dense full-body human-scene contact, 18- Reducing
footskate in human motion reconstruction with ground contact constraints]，来估计接触掩码

令 $\boldsymbol{p}_{t}^{\text {l-ankle }} \in \mathbb{R}^{3}$ 表示时刻 $t$ 左踝关节的位置， $c_{t}^{\text {left }} \in\{0,1\}$ 为对应的接触掩码。接触掩码的估计方式如下

$c_{t}^{\text {left }}=\mathbb{I}\left[\left\|\boldsymbol{p}_{t+1}^{\text {l-ankle }}-\boldsymbol{p}_{t}^{\text {l-ankle }}\right\|_{2}^{2}<\epsilon_{\text {vel }}\right] \cdot \mathbb{I}\left[p_{t, z}^{\text {l-ankle }}<\epsilon_{\text {height }}\right]$

其中 $\epsilon_{\mathrm{vel}}$ 和 $\epsilon_{\text {height }}$ 是通过经验选择的阈值，右脚的处理方式类似

为了解决阈值过滤未能消除的轻微悬浮伪影，作者基于估算的接触掩码应用了一个修正步骤

具体而言，如果在第 $t$ 帧任一只脚处于接触状态，则对全局平移施加一个垂直偏移。设 $\psi_{t}$ 表示时刻t的姿态全局平移，则修正后的垂直位置为

$\psi_{t, z}^{\mathrm{corr}}=\psi_{t, z}-\Delta h_{t}$

其中， $\Delta h_{t}=\min _{v \in \mathcal{V}_{t}} p_{t, z}^{v}$ 是帧 $t$ 时SMPL 网格顶点 $\mathcal{V}_{t}$ 中最低的z 坐标。虽然该修正减轻了漂浮伪影，但可能会导致帧间抖动。作者通过应用指数移动平均（EMA）来平滑运动，从而解决这一问题

第四，动作重定向

作者采用一种基于逆向运动学（IK）的方法 [19- Mink: Python inverse kinematics based on MuJoCo]，将处理后的 SMPL 格式动作重定向到G1 机器人。该方法将问题表述为可微分的优化问题，在保证末端执行器轨迹对齐的同时，遵循关节限制
为了增强动作多样性，作者引入了来自开源数据集 AMASS [4] 和 LAFAN [20-Robust motion in-betweening] 的额外数据
这些动作部分通过他们的流程进行处理，包括接触掩码估计、动作校正和动作重定向

如原论文附录B所述，他们的数据集整合了以下两类动作：

基于视频的来源，通过他们提出的多步动作处理流程提取动作数据。该流程的超参数如表3所示

开源数据集：选自AMASS和LAFAN的数据。该数据集包含13种不同的动作，并根据难度分为三个等级：简单、中等和困难
为了保证动作之间的平滑过渡，作者在每个序列的开始和结束处进行线性插值，使其从默认姿势过渡到参考动作，再返回默认姿势
具体细节见表4

1.2.2 自适应动作追踪：指数形式的跟踪奖励、最优跟踪因子、自适应机制

1.2.2.1 指数形式的跟踪奖励

PBHC中的奖励函数（详见附录C.2）由两个部分组成：

任务特定奖励，用于确保对参考动作的精确跟踪
以及正则化奖励，用于提升整体的稳定性和平滑性

任务特定的奖励包括用于对齐关节状态、刚体状态和足部接触掩码的项。除了足部接触跟踪项外，这些奖励均采用如下的指数形式——如下公式4 所示：

$r(x)=\exp (-x / \sigma)$

其中， $x$ 表示跟踪误差，通常以关节角等量的均方误差（MSE）来衡量，而 $\sigma$ 用于控制误差的容忍度，被称为跟踪因子。相比于负误差形式，这种指数形式因其有界性，有助于稳定训练过程，并为奖励权重分配提供了更直观的方法，因此更受青睐

直观来看，当 $\sigma$ 远大于 $x$ 的典型取值范围时，奖励值会保持接近1，并且对 $x$ 的变化变得不敏感
而当 $\sigma$ 过小时，奖励值趋近于0，同样会降低其敏感度
这凸显了合理选择 $\sigma$ 以提升响应性和追踪精度的重要性

该直观理解如图2所示

1.2.2.2 最优跟踪因子

为了确定最优跟踪因子的选择，作者提出一种简化的运动跟踪模型，并将其表述为一个双层优化问题

该表述的直观想法是，应选择跟踪因子 $\sigma$ ，以最小化收敛策略在参考轨迹上的累积跟踪误差。在手动调参的情况下，这通常通过一个迭代过程实现：工程师选择一个 $\sigma$ 值，训练策略，观察结果，并重复这一过程，直到获得令人满意的性能

给定一个策略 $\pi$ ，存在一个长度为 $N$ 的期望跟踪误差序列 $\boldsymbol{x} \in \mathbb{R}_{+}^{N}$ ，其中 $x_{i}$ 表示在第 $i$ 步rollout 过程中期望的跟踪误差
作者并不直接优化策略，而是将跟踪误差序列 $x$ 作为决策变量

这使他们能够将运动跟踪的优化问题重新表述为——如下公式5 所示
$\max _{\boldsymbol{x} \in \mathbb{R}_{+}^{N}} J^{\text {in }}(\boldsymbol{x}, \sigma)+R(\boldsymbol{x})$
其中
$\rightarrow$ 对于公式中的第一部分，内部目标 $J^{\text {in }}(\boldsymbol{x}, \sigma)=\sum_{i=1}^{N} \exp \left(-x_{i} / \sigma\right)$ 是由公式(4) $r(x)=\exp (-x / \sigma)$ 中的跟踪奖励诱导的简化累计奖励
$\rightarrow$ 对于公式中的第二部分，作者引入 $R(\boldsymbol{x})$ 以捕捉除 $J^{\text {in }}$ 以外的所有附加效应，包括环境动态和其他策略目标(如额外奖励)
方程(5)的解 $x^{*}$ 对应于最优策略 $\pi^{*}$ 所引起的误差序列
随后， $\sigma$ 的优化目标是最大化获得的累计负跟踪误差 $J^{\mathrm{ex}}\left(\boldsymbol{x}^{*}\right)=\sum_{i=1}^{N}-x_{i}^{*}$ ，即外部目标，可形式化为以下双层优化问题——如下公式6 所示
$\max _{\sigma \in \mathbb{R}_{+}} J^{\mathrm{ex}}\left(\boldsymbol{x}^{*}\right), \quad \text { s.t. } \quad \boldsymbol{x}^{*} \in \arg \max _{\boldsymbol{x} \in \mathbb{R}_{+}^{N}} J^{\text {in }}(\boldsymbol{x}, \sigma)+R(\boldsymbol{x})$

在额外的技术假设下，可以求解公式(6)，并推导出最优跟踪因子是最优跟踪误差的平均值，如下公式7所示(具体细节见附录A)
$\sigma^{*}=\left(\sum_{i=1}^{N} x_{i}^{*}\right) / N$

如原论文附录A所述，来看下最优跟踪Sigma的推导

回顾公式6中的双层优化问题，具体如下——分别定义为9a/9b
$\begin{aligned} \max _{\sigma \in \mathbb{R}_{+}} & J^{\text {ex }}\left(\boldsymbol{x}^{*}\right) \\ \text { s.t. } & \boldsymbol{x}^{*} \in \arg \max _{\boldsymbol{x} \in \mathbb{R}_{+}^{N}} J^{\text {in }}(\boldsymbol{x}, \sigma)+R(\boldsymbol{x}) \end{aligned}$
假设 $R(\boldsymbol{x})$ 取线性形式 $R(\boldsymbol{x})=\boldsymbol{A} \boldsymbol{x}+\boldsymbol{b}$ ， $J^{\mathrm{ex}}$ 和 $J^{\mathrm{in}}$ 是两次连续可微的，并且下层问题方程(9b) 存在唯一解 $\boldsymbol{x}^{*}(\sigma)$
因此，作者采用隐式梯度方法来求解
$J^{\mathrm{ex}}$ 关于 $\sigma$ 的梯度为——公式10
$\frac{d J^{\mathrm{ex}}}{d \sigma}={\frac{d \boldsymbol{x}^{*}(\sigma)^{\top}}{d \sigma}}^{\top} \nabla_{\boldsymbol{x}} J^{\mathrm{ex}}\left(\boldsymbol{x}^{*}(\sigma)\right)$

要想得到上面公式10中等号右边的这个 $\frac{dx^*(\sigma)}{d\sigma}$ ，由于 $x^*(\sigma)$ 是一个低层解，它满足——公式11
$\nabla_{\boldsymbol{x}}\left(J^{\text {in }}\left(\boldsymbol{x}^{*}(\sigma), \sigma\right)+R(\boldsymbol{x})\right)=0$
对公式（11）关于σ求一阶导数，得到——公式12和公式13：
$\begin{array}{c} \frac{d}{d \sigma}\left(\nabla_{\boldsymbol{x}}\left(J^{\text {in }}\left(\boldsymbol{x}^{*}(\sigma), \sigma\right)+R(\boldsymbol{x})\right)=\nabla_{\sigma, \boldsymbol{x}}^{2} J^{\text {in }}+{\frac{d \boldsymbol{x}^{*}(\sigma)}{d \sigma}}^{\top} \nabla_{\boldsymbol{x}, \boldsymbol{x}}^{2} J^{\text {in }}=0\right. \\ {\frac{d \boldsymbol{x}^{*}(\sigma)^{\top}}{d \sigma}}^{\top}=-\nabla_{\sigma, \boldsymbol{x}}^{2} J^{\text {in }}\left(\boldsymbol{x}^{*}(\sigma), \sigma\right) \nabla_{\boldsymbol{x}, \boldsymbol{x}}^{2} J^{\text {in }}\left(\boldsymbol{x}^{*}(\sigma), \sigma\right)^{-1} \end{array}$

将公式（13）代入公式（10），得到公式14
$\frac{d J^{\mathrm{ex}}}{d \sigma}=-\nabla_{\sigma, \boldsymbol{x}}^{2} J^{\mathrm{in}}\left(\boldsymbol{x}^{*}(\sigma), \sigma\right) \nabla_{\boldsymbol{x}, \boldsymbol{x}}^{2} J^{\mathrm{in}}\left(\boldsymbol{x}^{*}(\sigma), \sigma\right)^{-1} \nabla_{\boldsymbol{x}} J^{\mathrm{ex}}\left(\boldsymbol{x}^{*}(\sigma)\right)$

很好，继续往下
对于公式14中，有以下的公式15(a)和15(b)
$\begin{aligned} J^{\mathrm{ex}}(\boldsymbol{x}) & =\sum_{i=1}^{N}-x_{i} \\ J^{\mathrm{in}}(\boldsymbol{x}, \sigma) & =\sum_{i=1}^{N} \exp \left(-x_{i} / \sigma\right) \end{aligned}$
在公式（14）中计算一阶和二阶梯度如下——分别得到公式16a/16b/16c/16d
$\begin{aligned} \nabla_{\boldsymbol{x}} J^{\text {in }}(\boldsymbol{x}, \sigma) & =\exp (-\boldsymbol{x} / \sigma)\left(-\frac{1}{\sigma}\right) \\ \nabla_{\boldsymbol{x}} J^{\text {ex }}(\boldsymbol{x}) & =\mathbf{1} \\ \nabla_{\sigma, \boldsymbol{x}}^{2} J^{\text {in }}(\boldsymbol{x}, \sigma) & =\frac{\sigma-\boldsymbol{x}}{\sigma^{3}} \odot \exp (-\boldsymbol{x} / \sigma), \\ \nabla_{\boldsymbol{x}, \boldsymbol{x}}^{2} J^{\text {in }}(\boldsymbol{x}, \sigma) & =\operatorname{diag}(\exp (-\boldsymbol{x} / \sigma)) / \sigma^{2} \end{aligned}$

其中⊙表示按元素相乘
将(16)代入(14)，并令梯度等于零 $\frac{d J^{e x}}{d \sigma}=0$ ，则有公式17
$\sigma=\frac{\sum_{i=1}^{N} x_{i}^{*}(\sigma)}{N}$

1.2.2.3 自适应机制

虽然公式(7)为确定跟踪因子提供了理论指导

但 $\sigma^{*}$ 与 $x^{*}$ 之间的耦合关系导致出现循环依赖，无法直接计算
此外，由于参考动作数据的质量和复杂度各异，选取一个对所有动作场景都适用的单一固定跟踪因子是不现实的
为了解决这一问题，作者设计了一种自适应机制，通过误差估计与跟踪因子调整之间的反馈回路，在训练过程中动态调整 $\sigma$

在该机制中，作者维护了一个关于环境步数的即时跟踪误差的指数移动平均 $\text { (EMA) } \hat{x}$
该EMA 作为当前策略下期望跟踪误差的在线估计值，在训练过程中，这一数值应当接近当前因子 $\sigma$ 下的平均最优跟踪误差 $\left(\sum_{i=1}^{N} x_{i}^{*}\right) / N$

在每一步，PBHC 将 $\sigma$ 更新为当前的 $\hat{x}$ 值，从而形成一个反馈回路，使得跟踪误差的减少导致 $\sigma$ 的收紧。这个闭环过程推动策略的进一步优化，随着跟踪误差的降低，系统收敛到一个最优的 $\sigma$ 值，从而渐近地求解方程(9)，如图3 所示
为了确保训练过程中的稳定性，作者将σ 限制为非递增，并用一个相对较大的值 $\sigma^{\text {init }}$ 进行初始化。更新规则由公式(8) 给出
$\sigma \leftarrow \min (\sigma, \hat{x})$
如图4 所示，这一自适应机制使策略能够在训练过程中逐步提高其跟踪精度

1.2.3 RL训练框架：非对称Actor-Critic、奖励向量化、参考状态初始化、仿真到现实迁移

非对称Actor-Critic。遵循以往的工作[6,21]，引入了时间相位变量 $\phi_{t} \in[0,1]$ ，用于线性表示参考运动的当前进度，其中 $\phi_{t}=0$ 表示运动的开始， $\phi_{t}=1$ 表示运动的结束

actor的观测 $s_{t}^{\text {actor }}$ 包括
$\rightarrow$ 机器人的本体感知 $\boldsymbol{s}_{t}^{\text {prop }}$
而本体感知 $\boldsymbol{s}_{t}^{\text {prop }}=\left[\boldsymbol{q}_{t-4: t}, \dot{\boldsymbol{q}}_{t-4: t}, \boldsymbol{\omega}_{t-4: t}^{\text {root }}, \boldsymbol{g}_{t-4: t}^{\text {proj }}, \boldsymbol{a}_{t-5: t-1}\right]$ ，包括
关节位置 $\mathbf{q}_{t} \in \mathbb{R}^{23}$ 的5 步历史
关节速度 $\dot{\boldsymbol{q}}_{t} \in \mathbb{R}^{23}$
根部角速度 $\boldsymbol{\omega}_{t}^{\text {root }} \in \mathbb{R}^{3}$
根部投影重力 $\boldsymbol{g}_{t}^{\text {proj }} \in \mathbb{R}^{3}$
以及上一步动作 $\boldsymbol{a}_{t-1} \in \mathbb{R}^{23}$

$\rightarrow$ 以及时间相位变量 $\phi_{t}$

critic接收增强观测 $\boldsymbol{s}_{t}^{\text {crtic }}$ ，包括 $\boldsymbol{s}_{t}^{\text {prop }}$ 、时间相位、参考运动位置、根部线速度以及一组随机化物理参数
奖励向量化
为了便于学习具有多个奖励的价值函数，作者将奖励和价值函数向量化为： $\boldsymbol{r}=\left[r_{1}, \ldots, r_{n}\right]$ 和 $\boldsymbol{V}(s)=\left[V_{1}(s), \ldots, V_{n}(s)\right]$ ，遵循Xie 等人[22] 的方法

与将所有奖励聚合为单一标量不同，每个奖励分量 $r_{i}$ 被分配给一个价值函数 $V_{i}(s)$ ，该函数独立地估计回报，由具有多个输出头的critic网络实现。所有价值函数被聚合以计算动作优势。这一设计实现了精确的价值估计，并促进了策略优化的稳定性
参考状态初始化
作者采用参考状态初始化（RSI）[21]，该方法从参考动作的不同时间相位中随机采样，并以此初始化机器人的状态。这一做法有助于并行学习不同的动作阶段，从而显著提升训练效率
仿真到现实迁移
为弥合仿真与现实之间的差距，作者采用领域随机化方法，通过改变仿真环境和人形机器人的物理参数来实现。经过训练的策略会先通过仿真到仿真的测试进行验证，然后直接部署到真实机器人上，实现无需微调的零样本仿真到现实迁移。详细内容见附录C.3

如原论文附录C.1所述

对于观测空间设计
Actor 观察空间：Actor 的观测 $\boldsymbol{s}_{t}^{\text {actor }}$ 包括机器人本体感觉状态 $\boldsymbol{s}_{t}^{\text {prop }}$ 的5 步历史以及时间相位变量 $\phi_{t}$
Critic 观察空间：Critic 的观测 $\boldsymbol{s}_{t}^{\text {crtic }}$ 还包括基座线速度、参考运动的身体位置、当前与参考身体位置之间的差异，以及一组领域随机化的物理参数。详细信息见表5
在领域随机化中使用的若干随机物理参数被纳入critic观测范围，以提升价值估计的鲁棒性。领域随机化的详细设置见附录C.3
对于奖励设计
所有奖励函数详见表6
他们的奖励设计主要包括两部分：任务奖励和正则化奖励
具体而言，当关节位置超过软限制时，会施加惩罚。软限制是通过将硬限制按固定比例（α=0.95）对称缩放得到的
$\begin{aligned} \boldsymbol{m} & =\left(\boldsymbol{q}_{\min }+\boldsymbol{q}_{\max }\right) / 2 \\ \boldsymbol{d} & =\boldsymbol{q}_{\max }-\boldsymbol{q}_{\min } \\ \boldsymbol{q}_{\mathrm{soft}-\min } & =\boldsymbol{m}-0.5 \cdot \boldsymbol{d} \cdot \alpha \\ \boldsymbol{q}_{\mathrm{soft}-\max } & =\boldsymbol{m}+0.5 \cdot \boldsymbol{d} \cdot \alpha \end{aligned}$
其中 $q$ 表示关节位置。同样的方法也适用于计算关节速度 $\dot{\boldsymbol{q}}$ 和力矩 $\tau$ 的软限值

对于域随机化
为了提升他们训练策略在现实环境中的可迁移性，他们在训练过程中引入了域随机化，以增强从仿真到仿真以及从仿真到现实的鲁棒迁移能力
具体设置见表7

1.3 实验

在本节中，作者将通过实验评估 PBHC 的有效性。他们的实验旨在回答以下关键研究问题

Q1.他们的基于物理的动作过滤方法能否有效筛除不可跟踪的动作？
Q2.PBHC在仿真中相比以往方法是否实现了更优的跟踪性能？
Q3.自适应运动跟踪机制是否提升了跟踪精度？
Q4.PBHC在实际部署中表现如何？

1.3.1 实验设置：评估方法与指标

对于评估方法
作者采用通过所提出的运动处理流程（详见附录B）构建的高动态运动数据集，对策略的跟踪性能进行评估。相关示例见图5
他们根据动作的灵活性要求，将动作分为三个难度等级：简单、中等和困难。在每种设置下，策略均在IsaacGym[29]中使用三个不同的随机种子进行训练，并在1,000个回合的测试中进行评估

如原论文附录D.1所述，他们采用的计算平台、真实机器人设置分别如下所示

计算平台：每项实验均在配备24核Intel i7-13700 CPU（主频5.2GHz）、32GB内存和单块NVIDIA GeForce RTX 4090 GPU的机器上进行，操作系统为Ubuntu 20.04
且他们的的每个模型均训练27小时
真实机器人设置：他们在Unitree G1机器人上部署我们的策略
系统由车载运动控制板和外部PC组成，两者通过以太网连接
$\rightarrow$ 控制板采集传感器数据，并通过DDS协议传输至PC
$\rightarrow$ PC负责维护观测历史、执行策略推理，并将目标关节角度发送回控制板，控制板随后发出电机指令

对于指标
策略的跟踪性能通过以下指标进行量化：
全局平均每身体位置误差 $(E_{\mathrm{g}-\mathrm{mpbpe}}, \mathrm{~mm})$
即全局每个身体部位位置平均误差（Eg-mpbpe，毫米）：身体各部位在全局坐标系下的位置平均误差
$E_{\mathrm{g} \text {-mpbpe }}=\mathbb{E}\left[\left\|\boldsymbol{p}_{t}-\boldsymbol{p}_{t}^{\mathrm{ref}}\right\|_{2}\right]$

根相对平均每身体位置误差 $\left(E_{\text {mpbpe }}, \mathrm{mm}\right)$
即相对于根节点的每个身体部位位置平均误差（Empbpe，毫米）：身体各部位相对于根节点位置的平均误差
$E_{\text {mpbpe }}=\mathbb{E}\left[\left\|\left(\boldsymbol{p}_{t}-\boldsymbol{p}_{\text {root }, \mathrm{t}}\right)-\left(\boldsymbol{p}_{t}^{\text {ref }}-\boldsymbol{p}_{\text {root }, \mathrm{t}}^{\text {ref }}\right)\right\|_{2}\right]$

平均每关节位置误差 $\left(E_{\text {mpjpe }}, 10^{-3} \mathrm{rad}\right)$
即关节位置平均误差：关节旋转的平均角度误差
$E_{\mathrm{mpjpe}}=\mathbb{E}\left[\left\|\boldsymbol{q}_{t}-\boldsymbol{q}_{t}^{\mathrm{ref}}\right\|_{2}\right]$

平均每关节速度误差 $\left(E_{\text {mpjve }}, 10^{-3} \mathrm{rad} / \text { frame }\right)$
即平均每关节速度误差：关节角速度的平均误差
$E_{\text {mpjve }}=\mathbb{E}\left[\left\|\Delta \boldsymbol{q}_{t}-\Delta \boldsymbol{q}_{t}^{\text {ref }}\right\|_{2}\right]$
其中， $\Delta \boldsymbol{q}_{t}=\boldsymbol{q}_{t}-\boldsymbol{q}_{t-1}$

平均每身体速度误差 $\left(E_{\text {mpbve }}, \mathrm{mm} / \text { frame }\right)$
即身体部位速度平均误差（Empbve，毫米/帧）：身体各部位线速度的平均误差
$E_{\mathrm{mpbve}}=\mathbb{E}\left[\left\|\Delta \boldsymbol{p}_{t}-\Delta \boldsymbol{p}_{t}^{\mathrm{ref}}\right\|_{2}\right]$
其中， $\Delta \boldsymbol{p}_{t}=\boldsymbol{p}_{t}-\boldsymbol{p}_{t-1}$

以及平均每身体加速度误差 $\left(E_{\text {mpbae }}, \mathrm{mm} / \text { frame }^{2}\right)$
即平均每个身体部位加速度误差（Empbae , mm/frame2）：身体部位加速度的平均误差
$E_{\text {mpbae }}=\mathbb{E}\left[\left\|\Delta^{2} \boldsymbol{p}_{t}-\Delta^{2} \boldsymbol{p}_{t}^{\text {ref }}\right\|_{2}\right]$
其中 $\Delta^{2} \boldsymbol{p}_{t}=\Delta \boldsymbol{p}_{t}-\Delta \boldsymbol{p}_{t-1}$

1.3.2 运动过滤

为了解决Q1.他们的基于物理的动作过滤方法能否有效筛除不可跟踪的动作？作者对10个动作序列应用了基于物理的动作过滤方法（见§3.1）。其中，有4个序列因不符合过滤标准被剔除，其余6个序列被接受

为了评估过滤方法的有效性，为每个动作单独训练一个策略，并计算剧集长度比（ELR），即平均剧集长度与参考动作长度的比值

如图6所示

被接受的动作始终能够获得较高的ELR，这表明满足基于物理指标的动作能够在动作跟踪中实现更优的性能

相比之下，被拒绝的动作最大ELR仅为54%，这表明其经常违反终止条件。上述结果表明，作者的筛选方法能够有效排除本质上无法跟踪的动作，从而通过聚焦于可行候选项提升整体效率

1.3.3 主要结果

为了解决Q2.PBHC在仿真中相比以往方法是否实现了更优的跟踪性能？作者将PBHC与三种基线方法进行了比较：

OmniH2O [10]
Exbody2 [5]
MaskedMimic [23]

所有基线方法在跟踪参考动作时均采用了奖励函数的指数形式，具体如§3.2.1所述。实现细节详见附录D.3

如表1所示
PBHC在所有评估指标上均稳定优于基线方法OmniH2O和ExBody2
作者认为，这些提升归因于他们自适应的运动跟踪机制，该机制能够根据运动特征自动调整跟踪因子，而基线方法中固定且依赖经验调优的参数无法适应多样化的运动
MaskedMimic在某些指标上表现良好，但它主要用于角色动画，并不适用于机器人控制，因为它没有考虑诸如部分可观测性和动作平滑性等约束条件
因此，作者将其视为一种“oracle”风格的下界，而不是可以直接比较的基线方法

如原论文附录D.3所示，为确保公平对比，所有基线方法针对每种动作分别进行训练。他们考虑了以下基线方法

OmniH2O
OmniH2O 采用教师-学生训练范式。他们适度提高了跟踪奖励权重，以更好地适配 G1 机器人
在他们的设置中，教师策略和学生策略分别训练 20 小时和 10 小时
Exbody2
ExBody2采用了解耦的关键点-速度跟踪机制
教师策略和学生策略分别训练了20小时和10小时
MaskedMimic
MaskedMimic包括三个连续的训练阶段，他们仅使用第一个阶段，因为剩余阶段与他们的任务无关。该方法通过直接优化姿态级别的准确性来复现参考动作，而没有对物理合理性进行显式正则化
每个策略训练18小时

1.3.4 自适应运动跟踪机制的影响

为研究：Q3.自适应运动跟踪机制是否提升了跟踪精度

作者进行了消融实验，将作者的自适应运动跟踪机制（§3.2）与四种采用固定跟踪因子的基线配置进行对比：Coarse、Medium、UpperBound 和 LowerBound
这些配置中的跟踪因子从 Coarse、Medium、UpperBound 到 LowerBound 依次减小
其中 LowerBound 大致对应于训练收敛后自适应机制所得的最小跟踪因子，而UpperBound 则大致对应最大值。各基线的具体配置及自适应机制收敛后的跟踪因子详见附录 D.4

如原论文附录D.4所述

定义了五组跟踪因子：Coarse、Medium、UpperBound、LowerBound 以及 Ours的初始值，如表10所示

同时，作者在表11中提供了自适应机制收敛后的跟踪因子

如图7所示，固定跟踪因子配置（Coarse、Medium、LowerBound 和 UpperBound）的性能在不同运动类型之间存在差异

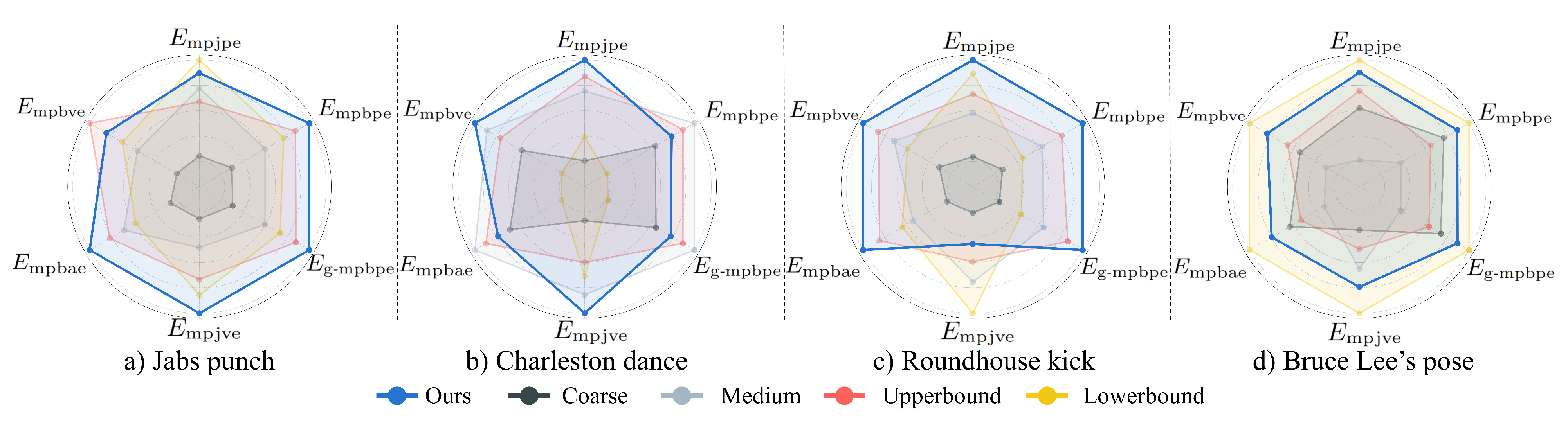
具体而言，虽然 LowerBound 和 UpperBound 在某些运动类型上表现出色，但在其他运动类型上表现不佳，这表明没有任何一种固定设置能够在所有运动中始终实现最优的跟踪效果
相比之下，作者的自适应运动跟踪机制能够在所有运动类型中始终实现接近最优的性能，充分证明了其根据不同运动特性动态调整跟踪因子的有效性

1.3.5 现实世界部署

如图8、图11及相关支持视频所示

他们的机器人在现实世界中通过多样化的高级技能展现出卓越的动态能力：

复杂的武术技巧，包括强有力的拳击组合（直拳、勾拳及马步冲拳）和高难度踢技（正踢、跳踢、侧踢、后踢及旋转鞭腿）
杂技动作，如完整的360度旋转
灵活的动作，包括深蹲和拉伸
艺术表演，从动感十足的舞蹈到优雅的太极序列

为了定量评估他们策略的跟踪性能，作者对太极动作进行了10次试验，并基于机载传感器读数计算评估指标，如表2所示「太极动作在现实世界与仿真环境中的跟踪性能对比。由于现实世界中无法访问，机器人根节点被固定在原点」

值得注意的是，现实世界中获得的指标与仿真到仿真平台MuJoCo上的结果高度一致，这表明我们的策略能够在保持高性能控制的同时，实现从仿真到现实的稳健迁移

1.4 结论、局限性、课程学习

1.4.1 结论与局限性

本文提出了PBHC，这是一种新颖的强化学习（RL）框架，用于人形机器人全身运动控制。通过基于物理的运动处理和自适应运动跟踪，该框架实现了卓越的高动态行为和优异的跟踪精度

实验结果表明，运动过滤指标能够高效地筛选出难以跟踪的轨迹，而自适应运动跟踪方法在跟踪误差方面始终优于基线方法

然而，他们的方法仍存在局限性

缺乏对环境的感知能力，例如地形感知和障碍物规避，这限制了其在非结构化现实环境中的部署
每个策略仅被训练用于模仿单一动作，这对于需要多样动作库的应用来说效率不高。他们将如何在保持高动态性能的同时实现更广泛技能泛化的问题留作未来研究

1.4.2 课程学习

为了模拟高动态动作，作者引入了两种课程机制：一种是终止课程，逐步降低对跟踪误差的容忍度；另一种是惩罚课程，逐步增加正则化项的权重，以促进更稳定且物理上更合理的行为

终止课程：当人形机器人的运动偏离参考超过终止阈值 $\theta$ 时，该回合将提前终止
在训练过程中，该阈值会逐步降低，以增加训练难度：
$\theta \leftarrow \operatorname{clip}\left(\theta \cdot(1-\delta), \theta_{\min }, \theta_{\max }\right)$

其中初始阈值 $\theta=1.5$ ，边界为 $\theta_{\min }=0.3$ , $\theta_{\max }=2.0$ ，衰减率 $\delta=2.5 \times 10^{-5}$
惩罚课程：为了在训练初期促进学习，同时逐步施加更强的正则化，作者引入了一个逐步递增的缩放因子 $\alpha$ ，用于调节惩罚项的影响
$\alpha \leftarrow \operatorname{clip}\left(\alpha \cdot(1+\delta), \alpha_{\min }, \alpha_{\max }\right), \quad \hat{r}_{\text {penalty }} \leftarrow \alpha \cdot r_{\text {penalty }}$

其中初始惩罚系数 $\alpha=0.1$ ，取值范围为 $\alpha_{\min }=0.0$ ， $\alpha_{\max }=1.0$ ，增长率 $\delta=1.0 \times 10^{-4}$