暑期算法训练.5

20. 力扣 34.在排序数组中查找元素的第一个位置和最后一个位置

20.1 题目解析：

20.2 算法思路：

20.3 代码演示：

编辑

20.4 总结反思：

21.力扣 69.x的平方根

21.1 题目解析：

21.2 算法思路：

21.3 代码演示：

21.4 总结反思：

22. 力扣 35.搜索插入位置

22.1 题目解析：

22.2 算法思路：

22.3 代码演示：

编辑

22.4 总结反思：

23 力扣. 852 山脉数组的封顶索引

23.1 题目解析：

23.2 算法思路：

23.3 代码演示：

23.4 总结反思：

24.力扣 162 寻找峰值：

24.1 题目解析：

编辑

24.2 算法思路：

24.3 代码演示：

24.4 总结反思：

25.力扣 LCR 173 点名

25.1 题目解析：

25.2 算法思路:

25.3 代码演示：

编辑

25.4 总结反思：

26 力扣 153.寻找旋转排序数组中的最小值

26.1 题目解析：

26.2 算法思路：

26.3 代码演示：

编辑

26.4 总结反思：

20. 力扣 34.在排序数组中查找元素的第一个位置和最后一个位置

20.1 题目解析：

题目很好理解，就是让你找出目标值的开始以及结束的位置。不过这道题目要注意处理一下，空数组以及没有结果的情况。

20.2 算法思路：

1.解法一就是暴力解法，就是遍历一遍数组，然后找出区间即可。这个的时间复杂度肯定是O（N）

2.解法二是咱们今天重点讲解的，就是用二分算法去解决这道题目。咱们直到，要想用二分算法，得先关注一下这道题目，得具有二段性才可以使用二分算法。升不升序倒是无所谓。因为你只要发现了规律，均可以使用二分算法。

【1】求区间左端点

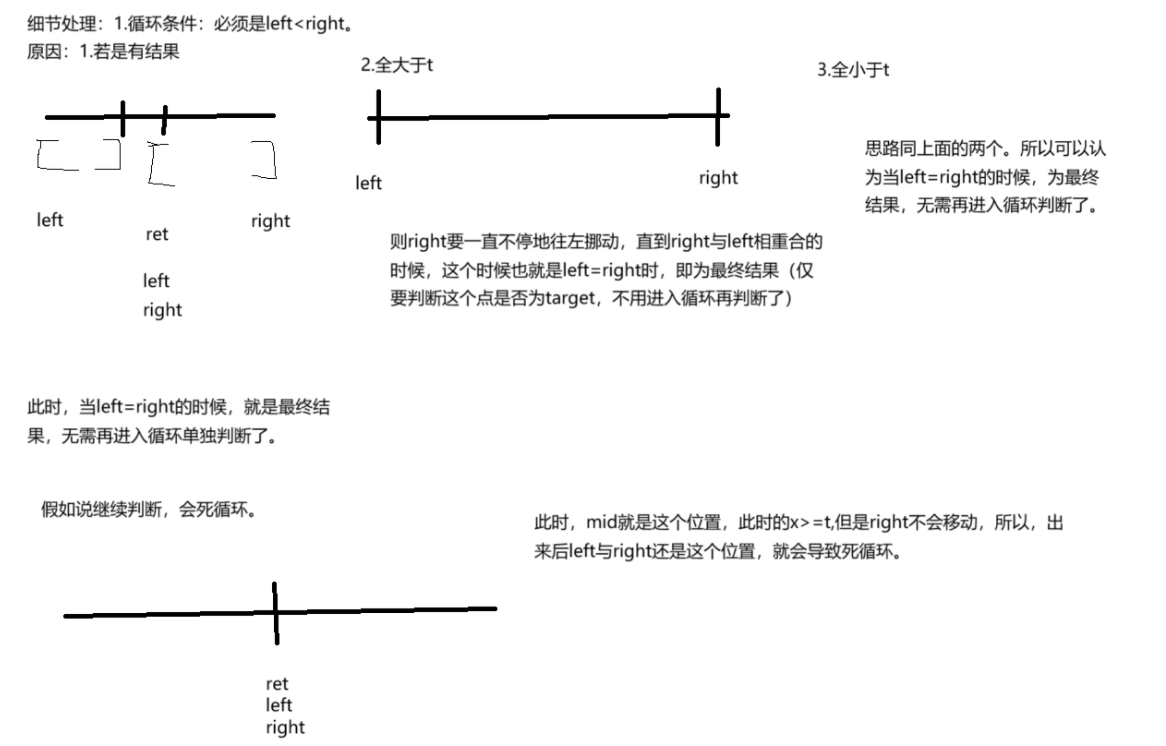
【2】求区间右端点

总结一下就是：

好了，这个题目的算法思路可算是写明白了。

20.3 代码演示：

vector<int> searchRange(vector<int>& nums, int target) {if (nums.size() == 0)  return { -1,-1 };//处理一下数组为空的情况int begin = 0;int left = 0; int right = nums.size() - 1;while (left < right){int mid = left + (right - left) / 2;if (nums[mid] < target) left = mid + 1;else right = mid;}//判断一下是否有结果，因为出了while循环后，left==rightif (nums[left] != target) return { -1,-1 };else begin = left;//这里写begin的目的仅仅是为了将left给存起来left = 0; right = nums.size() - 1;//其实，left直接从左端点开始就可以了while (left < right){int mid = left + (right - left + 1) / 2;if (nums[mid] <= target) left = mid;else right = mid - 1;}return { begin,right };//此时不需要判断是否有结果，因为只要有左端点，那么就一定有结果
}
int main()
{vector<int> nums = { 5,7,7,8,8,10 };int target = 8;vector<int> outcome = searchRange(nums, target);for (auto& e : outcome){cout << e << "";}cout << endl;return 0;
}

20.4 总结反思：

咱们来总结一下这类二分的模板：

不用死记硬背，只需要记住一点：就是若是下面出现了-1，那么上面mid给它加上1就可以了。

记住了求中点的方式，就可以推导出其他的了。

21.力扣 69.x的平方根

21.1 题目解析：

21.2 算法思路：

暴力解法很简单，就是遍历一边【0，x】内的数字i，若 i*i=x，直接返回x。若是i*i>x,则返回上一个数即可。

下面看解法二：

注意：寻找区间左端点，即找到大于等于目标值，说明右边还有满足条件的目标值（第一个满足条件的元素）。

寻找区间右端点：即找到小于等于目标值，说明右边不可能还有满足条件的目标值。（最后一个满足条件的元素）

所以说，为什么说这个寻找左端点是： < >=.原理上将等于归于右边，是因为若mid位于两个相等的值中间，此时不是最终结果。但你也可以想成，就是找左端点，右边肯定还有值。所以找右端点：左边还有值，就是<= >

所以本题是寻找k*k<=x,寻找右端点模板。

21.3 代码演示：

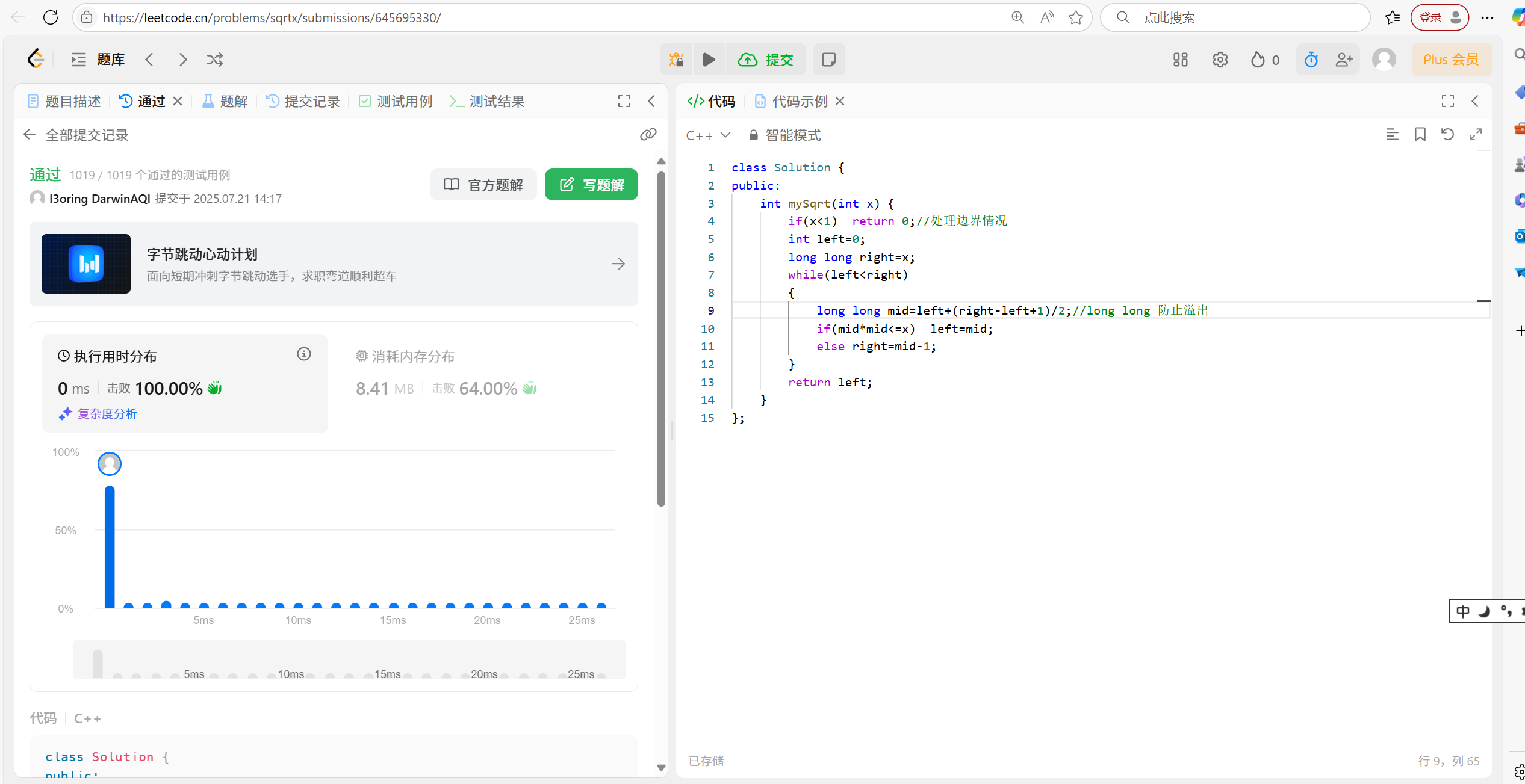
int mySqrt(int x) {if (x < 1)  return 0;//处理边界情况int left = 0;long long right = x;while (left < right){long long mid = left + (right - left + 1) / 2;//long long 防止溢出if (mid * mid <= x)  left = mid;else right = mid - 1;}return left;
}
int main()
{int x = 4;cout << mySqrt(x) << endl;return 0;
}

21.4 总结反思：

这个起始也就是一种二分算法的模板而已。

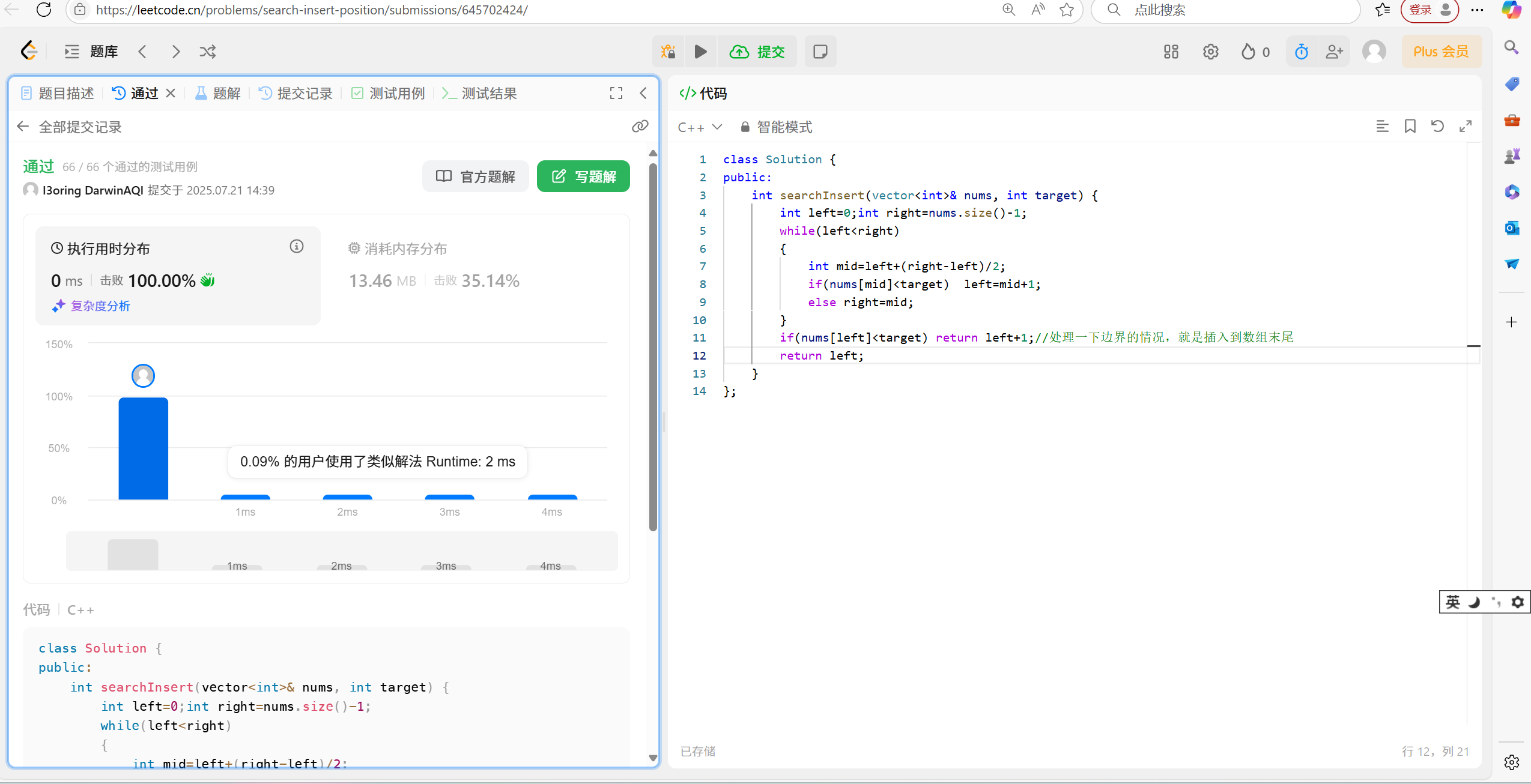
22. 力扣 35.搜索插入位置

22.1 题目解析：

注意关键句子：有序数组找到一个值。

22.2 算法思路：

1.找到了：直接返回下标即可。

2.若是没找到，就第一次出现了比目标值大的那个数（那个数大于等于目标值target）。或者数组末尾。

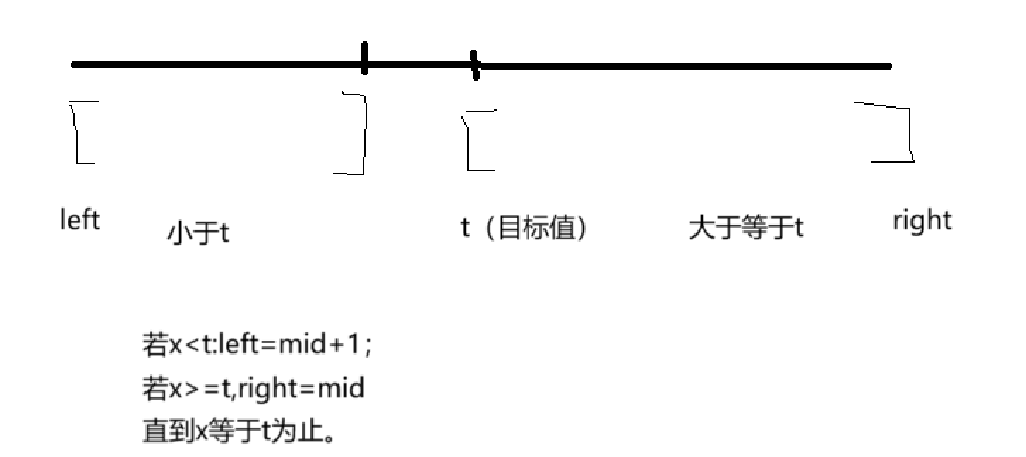这个mid（x）其实就是“那个数”，然后再继续进行判断即可。

22.3 代码演示：

int searchInsert(vector<int>& nums, int target) {int left = 0; int right = nums.size() - 1;while (left < right){int mid = left + (right - left) / 2;if (nums[mid] < target)  left = mid + 1;else right = mid;}if (nums[left] < target) return left + 1;//处理一下边界的情况，就是插入到数组末尾return left;
}
int main()
{vector<int> nums = { 1,3,5,6 };int target = 5;cout << searchInsert(nums, target) << endl;return 0;
}

22.4 总结反思：

这道题目是用到了求左端点的模板。要注意分清楚，还是挺好抓住的。

23 力扣. 852 山脉数组的封顶索引

23.1 题目解析：

就是让你找出山顶的索引。

23.2 算法思路：

就是找出最大的值呗。

1.暴力解法也好办，即使先遍历一遍数组，直至找到后一个数字比前一个数字小为止。返回那个数字的下标就可以了。

2.解法二就是二分查找算法：

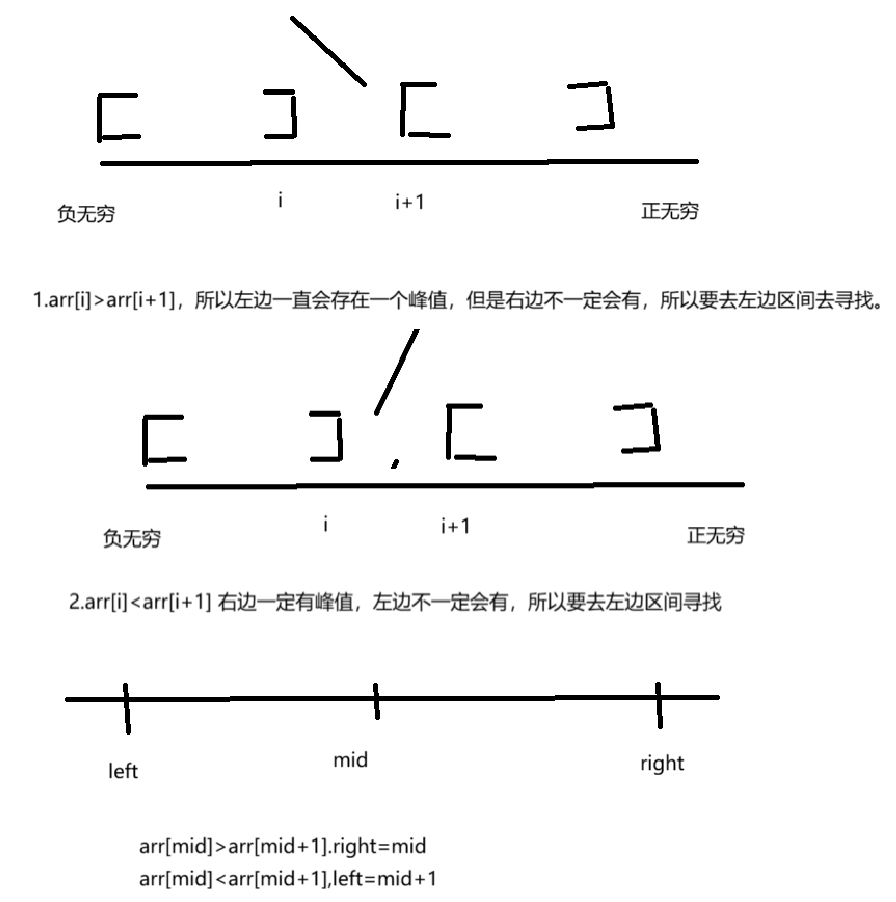
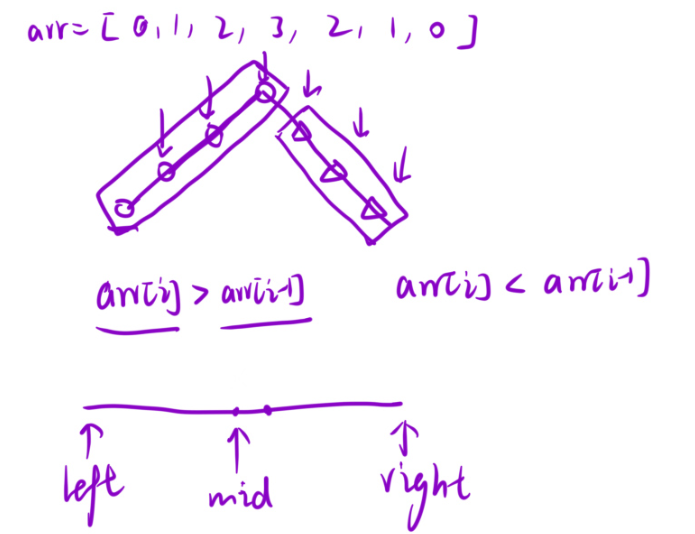那么这个时候：1.arr[mid]>arr[mid-1]（说明要到右区间去找），left=mid

2.arr[mid]<arr[mid-1]（说明要到左区间去找），即right=mid-1

mid位置呈现上升：那么接下来要在[mid+1,right]区间内搜索山峰。

mid位置呈现下降趋势，在[left,mid-1]区间内搜索山峰。

mid位置就是山峰，那么直接返回即可。

23.3 代码演示：

int peakIndexInMountainArray(vector<int>& arr) {int left = 0; int right = arr.size();while (left < right){int mid = left + (right - left + 1) / 2;if (arr[mid] > arr[mid - 1])  left = mid;else right = mid - 1;}return left;
}
int main()
{vector<int> arr = { 0,1,0 };cout << peakIndexInMountainArray(arr) << endl;return 0;
}

23.4 总结反思：

这道题目就不可以傻乎乎的再硬用了，需要分析一下为什么使用二分算法了。

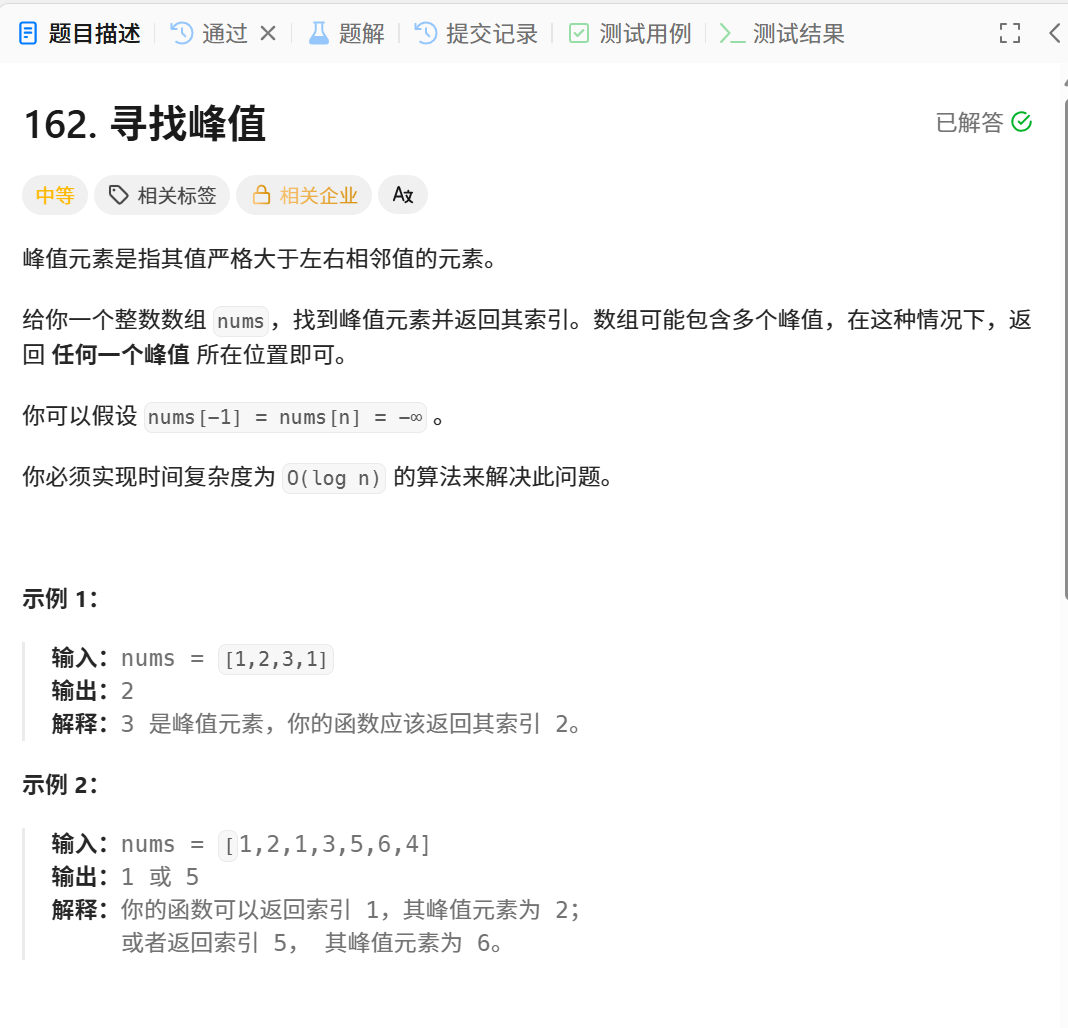
24.力扣 162 寻找峰值：

24.1 题目解析：

上一道题目是只有一个峰，但这个是有好多个峰，但是只返回任意一个峰即可。

并且题目中要求左，右，都可以是无穷小。

24.2 算法思路：

暴力解法：就是从第一个位置开始，一直向后走，分情况讨论：

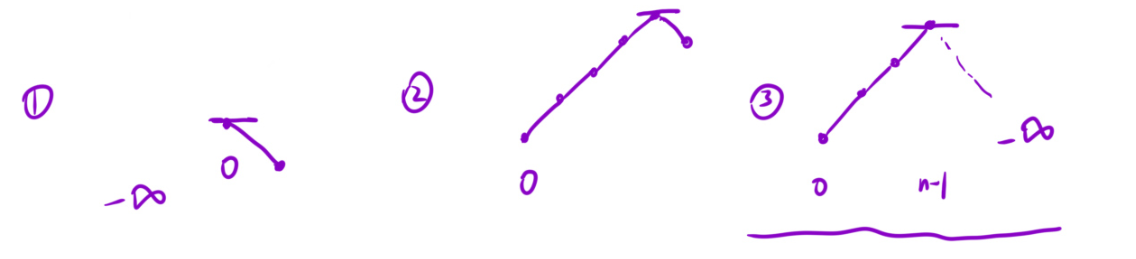
1.一开始就下降。2，上升着突然就下降了。3 一直向上走到最后一个位置。

2.二分算法：

这个mid应该就是随机选取的地方，然后再由这个分析规律（一开始，mid可能不等于你要求的那个值，只要是一个随机的值，但是循环完了，之后呢？left=right，此时的mid即为所求的值了。）

且上面所说的模板，若你right=mid-1，看到了减去一，那么在前面加上一就可以了。

24.3 代码演示：

int findPeakElement(vector<int>& nums) {int left = 0; int right = nums.size() - 1;while (left < right){int mid = left + (right - left) / 2;if (nums[mid] > nums[mid + 1]) right = mid;else left = mid + 1;}return left;
}int main()
{vector<int> nums = { 1,2,3,1 };cout << findPeakElement(nums) << endl;return 0;
}

24.4 总结反思：

这道题目也是考你灵活的运用二分模板。

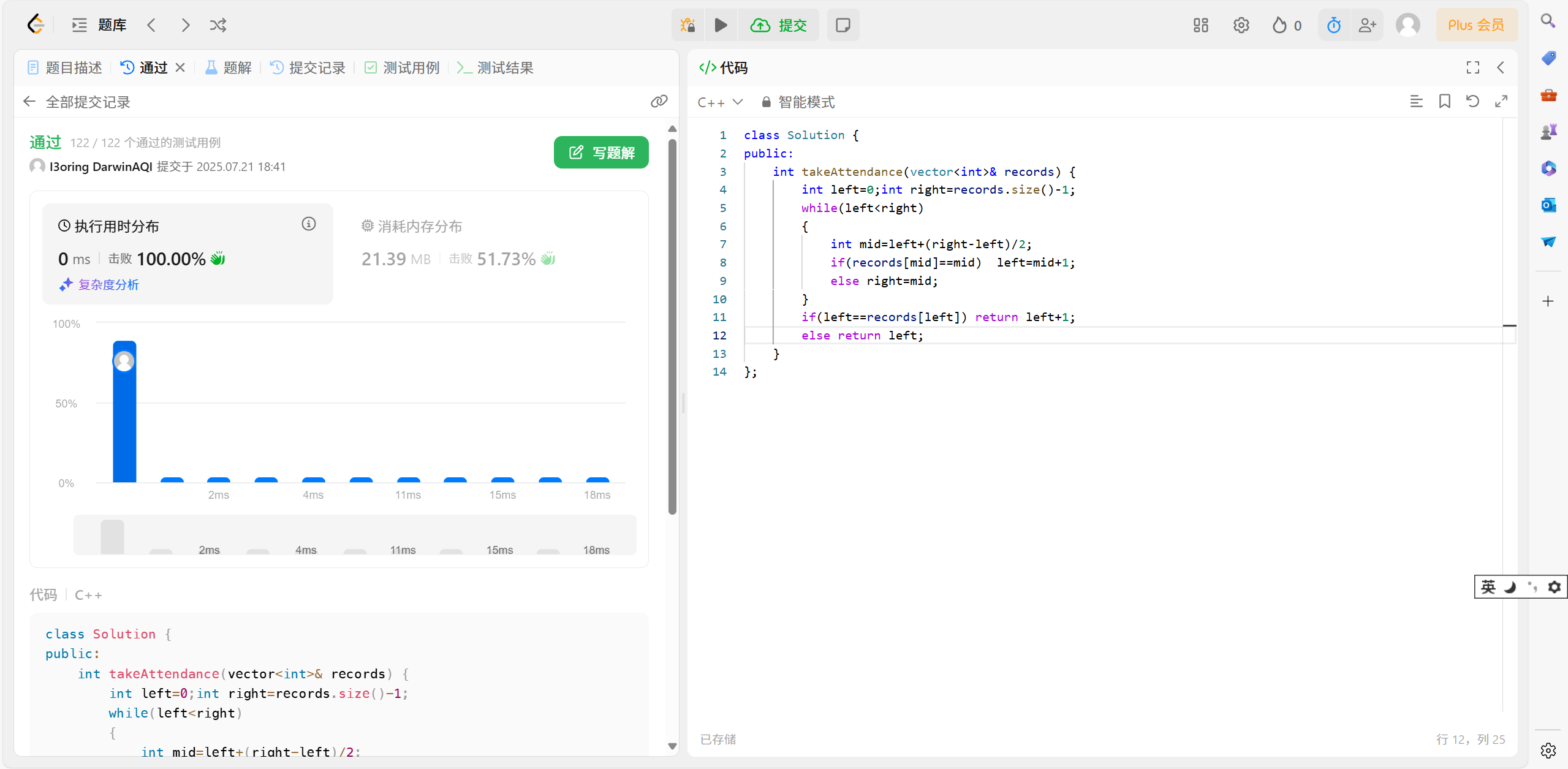
25.力扣 LCR 173 点名

25.1 题目解析：

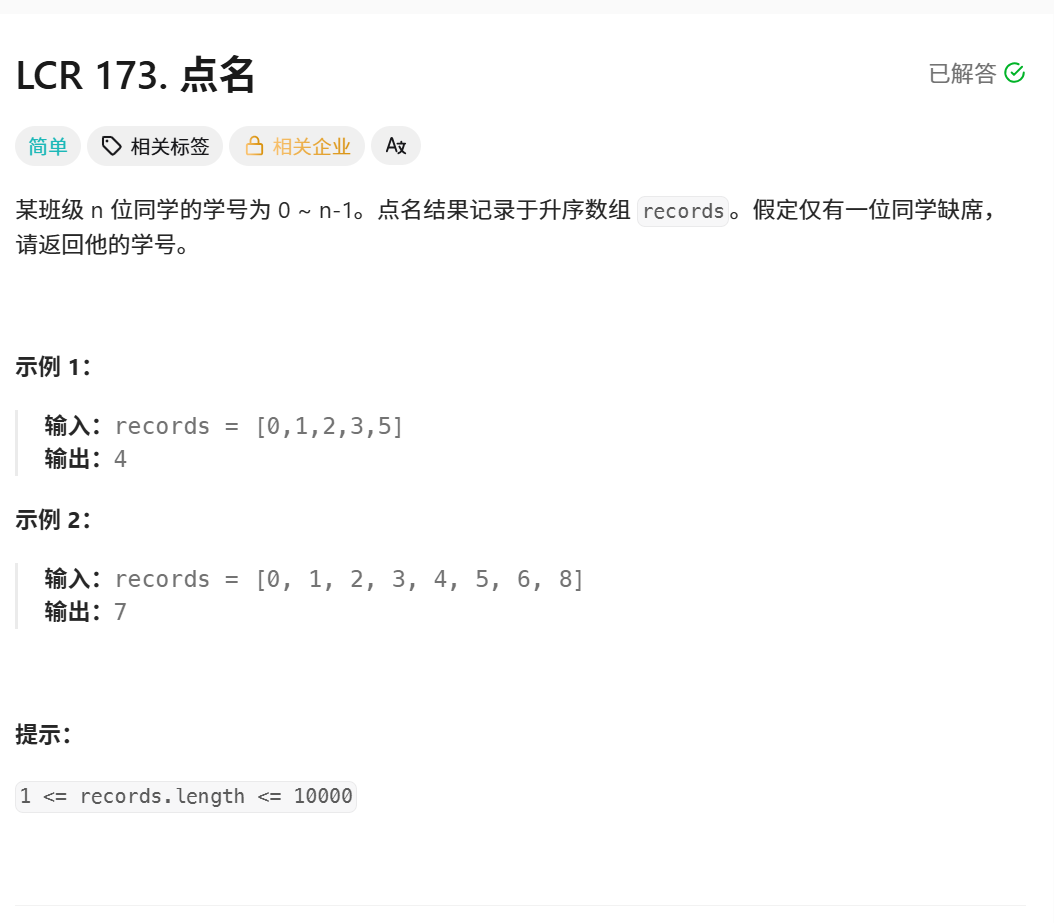这道题目就是让你找出缺失的数字

25.2 算法思路:

其实这道题目解法有很多，但是咱们今天在这里只讲二分算法：

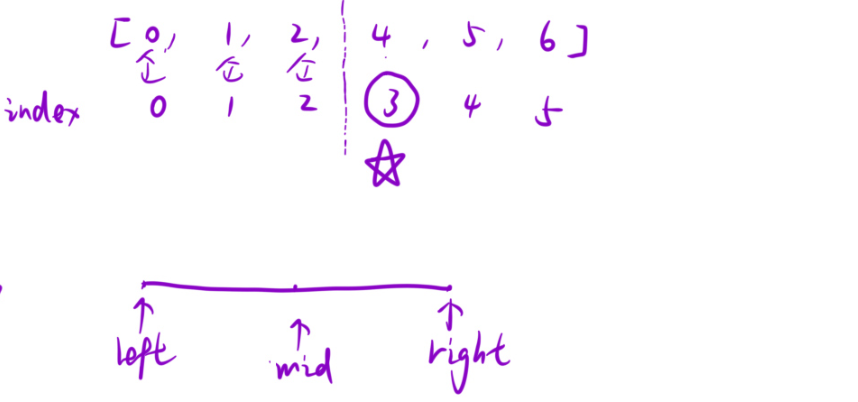
这个3就是区间的左端点。

1.左区间：若nums[mid]==mid,则left=mid+1；

2.右区间：nums[mid]!=mid,则right=mid

细节问题：边界：[0 ,1 ,2 ,3 ] 那么它缺的就是4.但是二分算法寻找的是右区间。但是这里没有右区间。所以，若最后一个值与下标值相同，则为完全递增数组，则返回left+1即可。

25.3 代码演示：

//点名
int takeAttendance(vector<int>& records) {int left = 0; int right = records.size() - 1;while (left < right){int mid = left + (right - left) / 2;if (records[mid] == mid)  left = mid + 1;else right = mid;}if (left == records[left]) return left + 1;else return left;
}
int main()
{vector<int> records = { 0,1,2,3,5 };cout << takeAttendance(records) << endl;return 0;
}

25.4 总结反思：

这道题目也是一道令人有想法的二分算法。

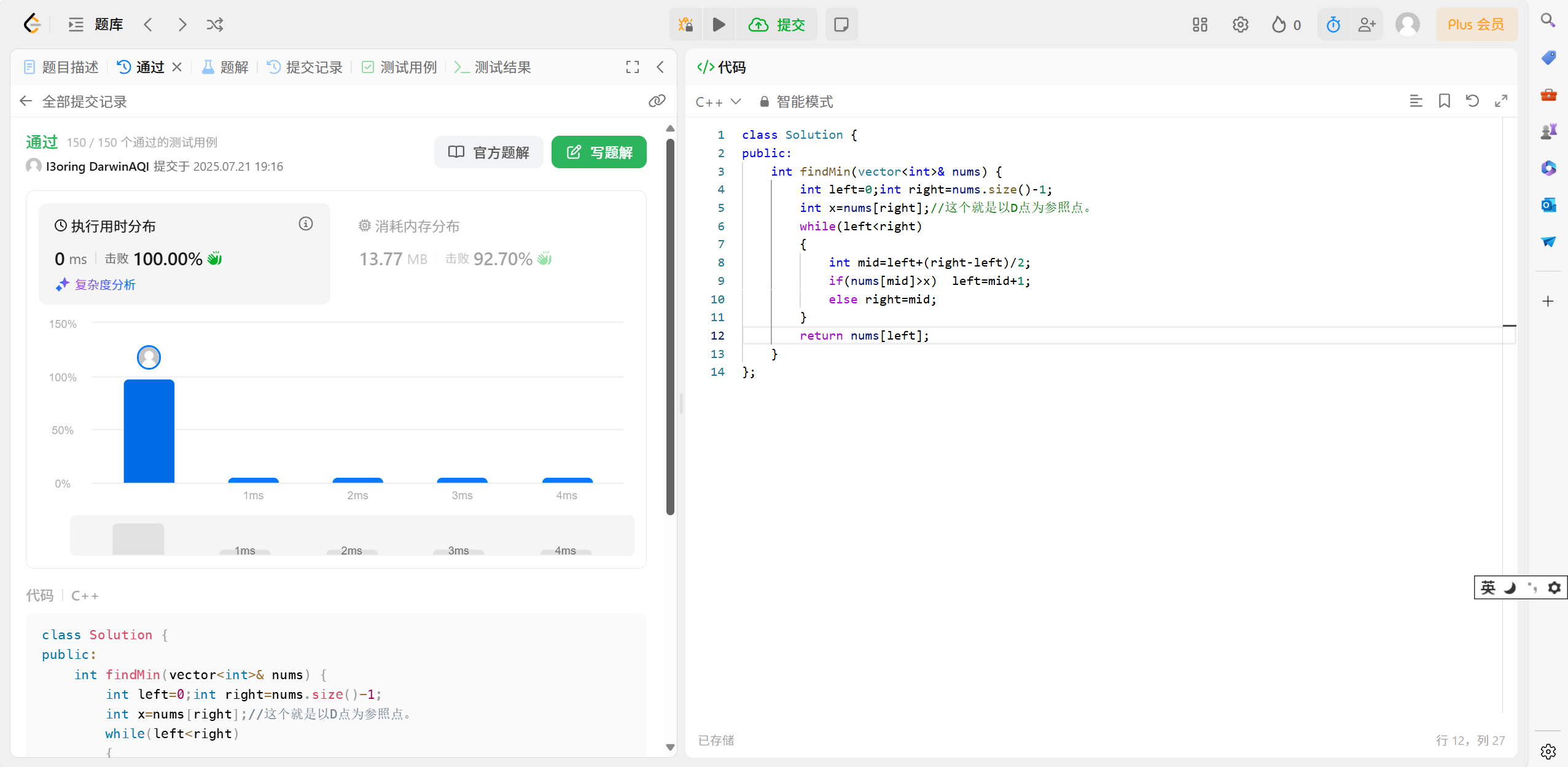
26 力扣 153.寻找旋转排序数组中的最小值

26.1 题目解析：

这道题目是我做的二分算法题目里面最不好理解的，也是最不好想的。题目很简单。咱们接下来看怎么做

26.2 算法思路：

咱们只讲二分算法：

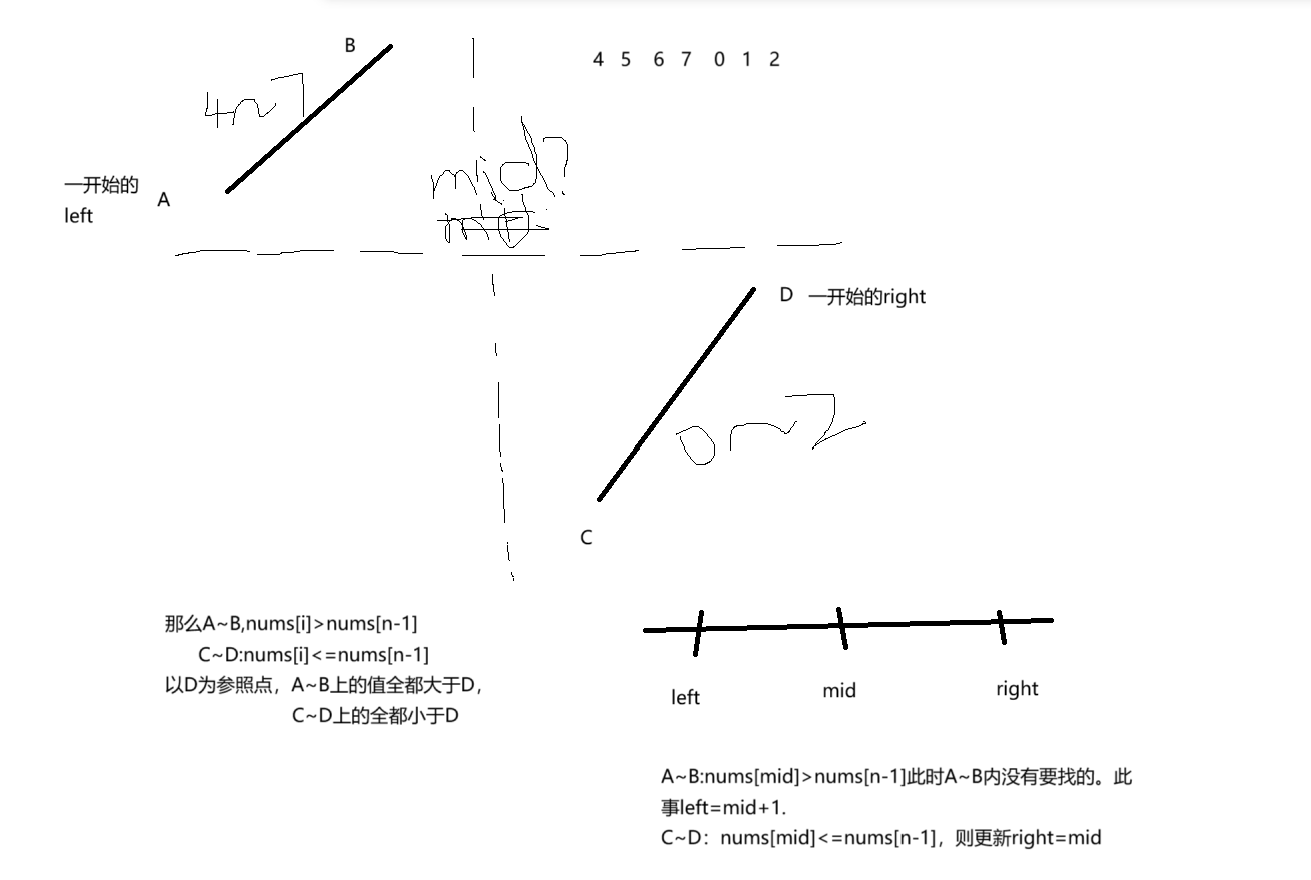
好，这个是以D点为参照点。那么以A点为参照点呢？

26.3 代码演示：

以D点为参照点：

//寻找旋转排序数组中的最小值
//以D点为参照点
int findMin(vector<int>& nums)
{int left = 0, right = nums.size() - 1;int x = nums[right]; // 标记⼀下最后⼀个位置的值(D点）while (left < right){int mid = left + (right - left) / 2;if (nums[mid] > x) left = mid + 1;else right = mid;}return nums[left];
}
int main()
{vector<int> nums1 = { 4,5,6,7,0,1,2 };vector<int> nums2 = { 3,4,5,1,2 };vector<int> nums3 = { 11,13,15,17 };cout << "nums1的最小值: " << findMin(nums1) << endl; // 输出0cout << "nums2的最小值: " << findMin(nums2) << endl; // 输出1cout << "nums3的最小值: " << findMin(nums3) << endl; // 输出11return 0;
}

以A点为参照点：

//以A点为参照点
int findMin(vector<int>& nums) {int left = 0;                  // A点，左边界int right = nums.size() - 1;// 数组未旋转的情况（完全升序）if (nums[left] <= nums[right]) {return nums[left];}// 二分查找while (left < right) {int mid = left + (right - left) / 2;// 中间元素大于左边界元素，说明左半部分有序，最小元素在右半部分if (nums[mid] > nums[left]) {left = mid;}// 中间元素小于左边界元素，说明最小元素在左半部分（包括mid）else {right = mid;}}// 循环结束时left == right，此时下一个元素即为最小值return nums[left + 1];
}
int main()
{vector<int> nums1 = { 4,5,6,7,0,1,2 };vector<int> nums2 = { 3,4,5,1,2 };vector<int> nums3 = { 11,13,15,17 };cout << "nums1的最小值: " << findMin(nums1) << endl; // 输出0cout << "nums2的最小值: " << findMin(nums2) << endl; // 输出1cout << "nums3的最小值: " << findMin(nums3) << endl; // 输出11return 0;
}