计算图

• 计算图（Computation Graph）是一种用于描述计算过程的图形化表示方法。

• 在深度学习中，计算图通常用于描述 网络结构、运算过程 和数据流向。

• 计算图是一种有向无环图，用图形方式来表示算子与变量之间的关系，直观高效。

• 它由节点（Node）和边（Edge）组成，如下图Netron库可视化的例子，其中节点表示操作或函数，边表示数据流向。

前向传播 与 反向传播

• 在Pytorch中，计算图的构建是通过神经网络的 前向传播 (forward) 过程完成的。

• 反向传播 根据计算图来计算梯度，从而进行参数更新。它为自动微分（automatic differentiation）提供了基础，使得深度学习框架能够自动计算梯度并进行反向传播。

静态计算图、动态计算图

计算图可以分为两种类型：静态计算图 和 动态计算图

• 静态计算图： 在静态计算图中，计算图在模型定义阶段就被固定下来，不会发生变化。典型的例子是 TensorFlow 1.x 中的计算图。在这种情况下，首先定义计算图，然后运行会话（session）来执行图中的操作。

• 动态计算图： 在动态计算图中，计算图在运行时根据输入数据的形状和大小动态构建。PyTorch 和 TensorFlow 2.x 采用了动态计算图的方式。在这种情况下，每次前向传播都会重新构建计算图，使得模型更加灵活。

在整个前向计算过程中，PyTorch采用 动态计算图 的形式进行组织，且在每次 前向传播时重新构建。
其他深度学习架构，如TensorFlow、Keras 一般为静态图。

叶子节点、非叶子节点、根节点

• 上面的计算图中，圆形表示变量，矩形表示算子，这些变量和算子构成了一个完整的前向传播过程
• 叶子节点 ： $x、w、b$ 为叶子节点，它们是用户创建的变量，不依赖于其他变量
• 非叶子节点 ： $y、z$为非叶子节点，它们是通过计算得到的变量
• 根节点 ： $z$ 为根节点，它之后不会再有后续的运算，我们一般让根节点来执行 反向传播方法 z.backward()

torch.tensor()的requires_grad参数

• 对于叶子节点（Leaf Node）的 张量Tensor，需要用 requires_grad 指明是否记录对其的操作运算，以便之后通过 反向传播求梯度。

• 一般仅对 叶子节点 设置 requires_grad， 这些叶子节点，一般就是网络中层的参数，他们一般都是 torch.nn.Parameter 对象，requires_grad 属性 默认为 True

• 叶子结点如果需要求导，requires_grad 需设置为 True，那么由这些叶子节点计算得出的非叶子节点，requires_grad 会自动置为True

import torchx = torch.tensor([2.0], requires_grad=True)   # 叶子节点
w = torch.tensor([3.0], requires_grad=True)   # 叶子节点
b = torch.tensor([1.0], requires_grad=True)   # 叶子节点y = w * x  # 非叶子节点
z = y + b  # 非叶子节点# 查看叶子节点和非叶子节点的 requires_grad 属性
print('x 的 requires_grad 属性:', x.requires_grad)
print('w 的 requires_grad 属性:', w.requires_grad)
print('b 的 requires_grad 属性:', b.requires_grad)
print('y 的 requires_grad 属性:', y.requires_grad)
print('z 的 requires_grad 属性:', z.requires_grad) 

grad_fn属性

• 通过运算创建的非叶子节点 tensor，会自动被赋予 grad_fn 属性，用于表明生成这个张量的操作
• 叶子节点的 grad_fn 为 None，因为它们不是通过其他操作计算得来的，而是网络的参数或输入数据

一些常见的 grad_fn 类型包括：

• <CatBackward>：表示这个张量是通过 torch.cat 操作得到的。
• <MatMulBackward>：表示这个张量是通过矩阵乘法操作得到的。
• <AddBackward>：表示这个张量是通过加法操作得到的。
• <AddmmBackward>：表示一个张量是通过 torch.addmm 操作得到的。
• <DivBackward>：表示这个张量是通过除法操作得到的。
• <ReLUBackward>：表示这个张量是通过 ReLU 激活函数得到的。

**import torch# 创建叶子节点张量
x = torch.tensor([2.0], requires_grad=True)
y = torch.tensor([3.0], requires_grad=True)# 创建非叶子节点张量，通过运算生成
z = x * y# 查看叶子节点和非叶子节点的 grad_fn 属性
print('x 的 grad_fn:', x.grad_fn) 
print('y 的 grad_fn:', y.grad_fn)
print('z 的 grad_fn:', z.grad_fn) **

反向传播

在反向传播中，以 loss（根节点 tensor ）为核心，步骤为：

1. 用 optimizer.zero_grad() 清空叶子节点梯度，避免多次 optimizer.step() 时梯度累加。
2. 调用 loss.backward() 反向传播，计算叶子节点梯度并存入 .grad 属性。
3. 执行 optimizer.step() ，依优化器算法和学习率，用 .grad 梯度更新叶子节点（即模型参数 ） 。

for epoch in range(epochs):model.train()for imgs, labels in train_loader        :# trainoptimizer.zero_grad()loss.backward()optimizer.step()

完整举例：

import torch# 输入张量 x， require_grad 属性默认为 False
x = torch.Tensor([2])# 初始化 权重参数w, 偏移量b，并设置 require_grad 属性为 True, 为自动求导
w = torch.randn(1, requires_grad=True)
b = torch.randn(1, requires_grad=True)# 实现向前传播
y = torch.mul(w, x)
z = torch.add(y, b)# 分别查看叶子节点 x, w, b 和 非叶子节点 y、z 的require_grad属性
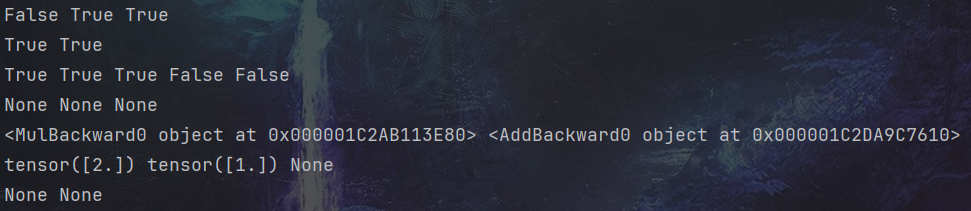
print(x.requires_grad, w.requires_grad, b.requires_grad)  # False True True
print(y.requires_grad, z.requires_grad )  # True True# 查看各节点是否为叶子节点
print(x.is_leaf, w.is_leaf, b.is_leaf, y.is_leaf, z.is_leaf)  # True True True False False# 分别查看 叶子节点 和 非叶子节点 的 grad_fn 属性
print(x.grad_fn, w.grad_fn, b.grad_fn)   # None None None
print(y.grad_fn, z.grad_fn)   # <MulBackward0 object at 0x7f8ac1303910> <AddBackward0 object at 0x7f8ac1303070># 反向传播计算梯度
z.backward()  # 查看叶子节点的梯度，x是叶子节点但它无须求导，故其梯度为None 
print(w.grad,b.grad,x.grad)  # tensor([2.]) tensor([1.]) None# 非叶子节点的梯度，执行backward之后，会自动清空 
print(y.grad,z.grad)  # None None

自动求导 Autograd

• 在神经网络中，一个重要内容就是进行参数学习，而参数学习的反向传播离不开求导。
• 现在大部分深度学习架构都有自动求导的功能，torch.autograd包 就是用来自动求导的。
• torch.autograd 包为张量上所有的操作提供了自动求导功能

实验：backward()反向传播自动求导

以下代码实现 ： 机器学习 回归问题举例，使用 backward() 反向传播自动求导，并手动更新参数

1. 先来造一批数据，作为样本数据 x 和 标签值y

import torch
import matplotlib.pyplot as plttorch.manual_seed(100)# 生成 x坐标数据，形状为 100 x 1
x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1)# 生成 y坐标数据，，形状为 100 x 1，加上一些噪声
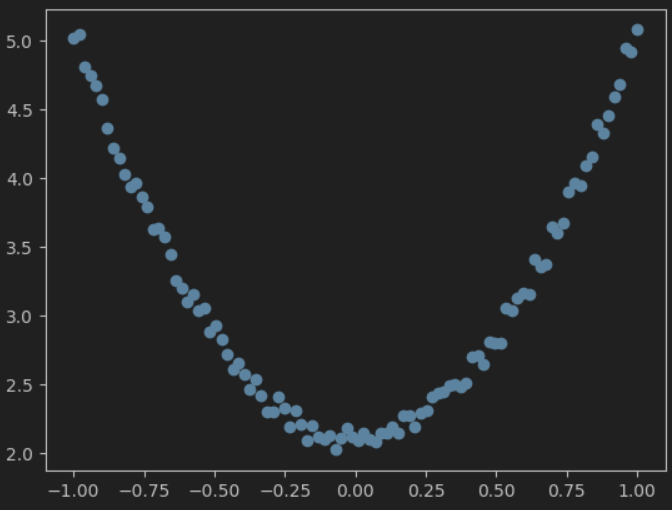
y = 3 * x.pow(2) + 2 + 0.2 * torch.rand(x.size())# 把tensor数据转换为numpy数据，并可视化
plt.scatter(x.numpy(), y.numpy())
plt.show()

2. 定义一个模型 y = wx +b, 我们要学习出 w 和 b 的值，用来拟合 x 和 y

# 初始化权重参数，参数 w、b 为需要学习的，故需要设置参数 requires_grad=True
w = torch.randn(1, 1, dtype=torch.float, requires_grad=True)
b = torch.zeros(1, 1, dtype=torch.float, requires_grad=True)
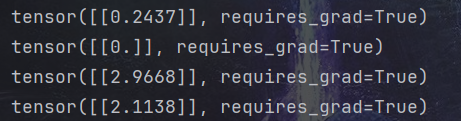
print(w)  # tensor([[1.1046]], requires_grad=True)
print(b)  # tensor([[0.]], requires_grad=True)lr = 0.001 # 学习率for i in range(800):# 向前传播，得到预测的y值，记为 y_predy_pred = w * x.pow(2) + b# 定义损失函数loss = (y - y_pred) ** 2loss = loss.sum()# 反向传播，自动计算梯度，存放在 grad 属性中loss.backward()# 手动更新参数，需要用torch.no_grad(), 使上下文环境中切断自动求导的计算with torch.no_grad():# 更新参数w -= lr * w.gradb -= lr * b.grad# 梯度清零w.grad.zero_()b.grad.zero_()print(w)  # tensor([[2.9668]], requires_grad=True)
print(b)  # tensor([[2.1138]], requires_grad=True)

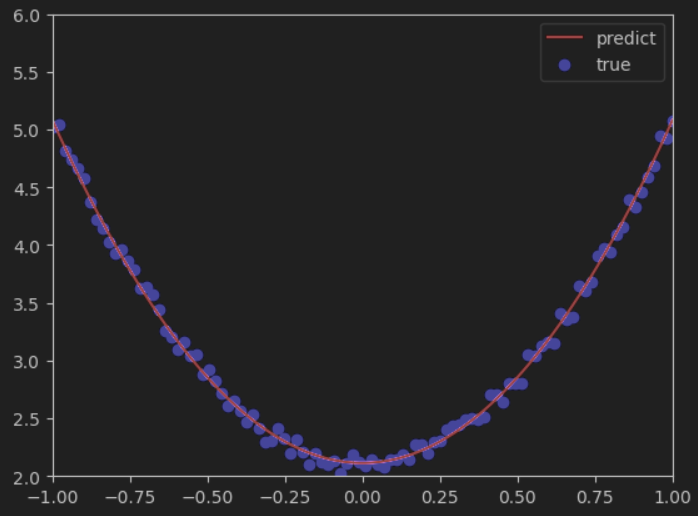
3. 可视化一下结果，红色曲线是预测结果 ，蓝色点是真实标签值