题目

题目链接🔗

在一个无限的 x 坐标轴上，有许多水果分布在其中某些位置。给你一个二维整数数组 fruits ，其中 fruits[i] = [positioni, amounti] 表示共有 amounti 个水果放置在 positioni 上。fruits 已经按 positioni 升序排列 ，每个 positioni 互不相同 。

另给你两个整数 startPos 和 k 。最初，你位于 startPos 。从任何位置，你可以选择 向左或者向右 走。在 x 轴上每移动 一个单位 ，就记作 一步 。你总共可以走 最多 k 步。你每达到一个位置，都会摘掉全部的水果，水果也将从该位置消失（不会再生）。

返回你可以摘到水果的 最大总数 。

示例 1：

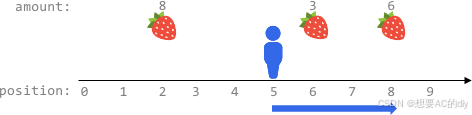
输入：fruits = [[2,8],[6,3],[8,6]], startPos = 5, k = 4
输出：9
解释：
最佳路线为：

• 向右移动到位置 6 ，摘到 3 个水果
• 向右移动到位置 8 ，摘到 6 个水果
  移动 3 步，共摘到 3 + 6 = 9 个水果

示例 2：

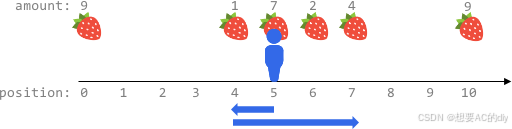
输入：fruits = [[0,9],[4,1],[5,7],[6,2],[7,4],[10,9]], startPos = 5, k = 4
输出：14
解释：
可以移动最多 k = 4 步，所以无法到达位置 0 和位置 10 。
最佳路线为：

• 在初始位置 5 ，摘到 7 个水果
• 向左移动到位置 4 ，摘到 1 个水果
• 向右移动到位置 6 ，摘到 2 个水果
• 向右移动到位置 7 ，摘到 4 个水果
  移动 1 + 3 = 4 步，共摘到 7 + 1 + 2 + 4 = 14 个水果

示例 3：

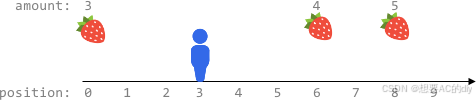
输入：fruits = [[0,3],[6,4],[8,5]], startPos = 3, k = 2
输出：0
解释：
最多可以移动 k = 2 步，无法到达任一有水果的地方

提示：

1 <= fruits.length <= 105
fruits[i].length == 2
0 <= startPos, positioni <= 2 * 105
对于任意 i > 0 ，positioni-1 < positioni 均成立（下标从 0 开始计数）
1 <= amounti <= 104
0 <= k <= 2 * 105

思路

本题的核心是求解从起始位置startPos出发，最多走k步所能摘到的最大水果数量。考虑到路径可能涉及向左或向右先走然后折返，我们可以枚举可能的右侧最远位置R（从startPos到startPos + k的范围），计算对应步数sr = R - startPos，然后计算在剩余步数下能到达的最左侧距离dd。dd通过两种策略计算：先向左走然后向右到R（dd <= (k - sr)/2），或先向右到R然后向左（dd <= k - 2*sr），取两种策略的最大dd，并clamp到[0, startPos]。使用数组arr存储每个位置的水果数量，left数组预计算从startPos向左的累加和。最后，对于每个R，计算从startPos - dd到R的水果总量，取最大值。这种方法高效地覆盖了所有可能路径，并确保在O(N)时间内求解，其中N = max(startPos, 最大位置) <= 4e5。

代码

C++

class Solution {
public:int maxTotalFruits(vector<vector<int>>& fruits, int startPos, int k) {int n = max(startPos, fruits.back()[0]);vector<int> arr(n + 1, 0);for(auto& x : fruits) arr[x[0]] += x[1];vector<int> left(n + 1, 0);// 向左走 startPos - i 步int last = 0;for(int i = startPos; i >= 0; i --) {left[startPos - i] = last + arr[i];last = left[startPos - i];}int x = 0, res = 0;for(int i = startPos; i <= min(startPos + k, n); i ++) {if(i != startPos) x += arr[i];int sr = i - startPos; // 向右走了 sr 步// 最多向左走了几步// l -> r// (k-sr)/2// r -> l// k - 2 * srres = max(res, x + left[min(startPos, max((k-sr)/2, k-2*sr))]);}return res;}
};

Java

class Solution {public int maxTotalFruits(int[][] fruits, int startPos, int k) {int n = Math.max(startPos, fruits[fruits.length - 1][0]);int[] arr = new int[n + 1];for (int[] x : fruits) {arr[x[0]] += x[1];}int[] left = new int[n + 1];int last = 0;for (int i = startPos; i >= 0; i--) {left[startPos - i] = last + arr[i];last = left[startPos - i];}int x = 0;int res = 0;int maxI = Math.min(startPos + k, n);for (int i = startPos; i <= maxI; i++) {if (i != startPos) {x += arr[i];}int sr = i - startPos;int cand1 = (k - sr) / 2;int cand2 = k - 2 * sr;int dd = Math.max(cand1, cand2);dd = Math.min(startPos, Math.max(0, dd));res = Math.max(res, x + left[dd]);}return res;}
}

Python

class Solution:def maxTotalFruits(self, fruits: List[List[int]], startPos: int, k: int) -> int:n = max(startPos, fruits[-1][0])arr = [0] * (n + 1)for p, a in fruits:arr[p] += aleft = [0] * (n + 1)last = 0for i in range(startPos, -1, -1):left[startPos - i] = last + arr[i]last = left[startPos - i]x = 0res = 0max_i = min(startPos + k, n)for i in range(startPos, max_i + 1):if i != startPos:x += arr[i]sr = i - startPoscand1 = (k - sr) // 2cand2 = k - 2 * srdd = max(cand1, cand2)dd = min(startPos, max(0, dd))res = max(res, x + left[dd])return res

复杂度分析

时间复杂度

O(N)，其中N = max(startPos, 最大位置) <= 4 \times 10^5，预计算left数组和循环枚举右侧位置均为O(N)。

空间复杂度

O(N)，用于存储arr和left数组。

结果

该解法通过了LeetCode的所有测试用例，运行时间和内存消耗均在可接受范围内。

总结

通过枚举右侧最远位置并计算最大左侧延伸距离，该方法巧妙地处理了路径折返的两种策略，确保了正确性和高效性。如果位置范围较大，可考虑使用前缀和优化进一步压缩空间，但当前实现已足够优秀。https://leetcode.cn/problems/maximum-fruits-harvested-after-at-most-k-steps/description/?envType=daily-question&envId=2025-08-03