Vanilla Convolution 普通卷积

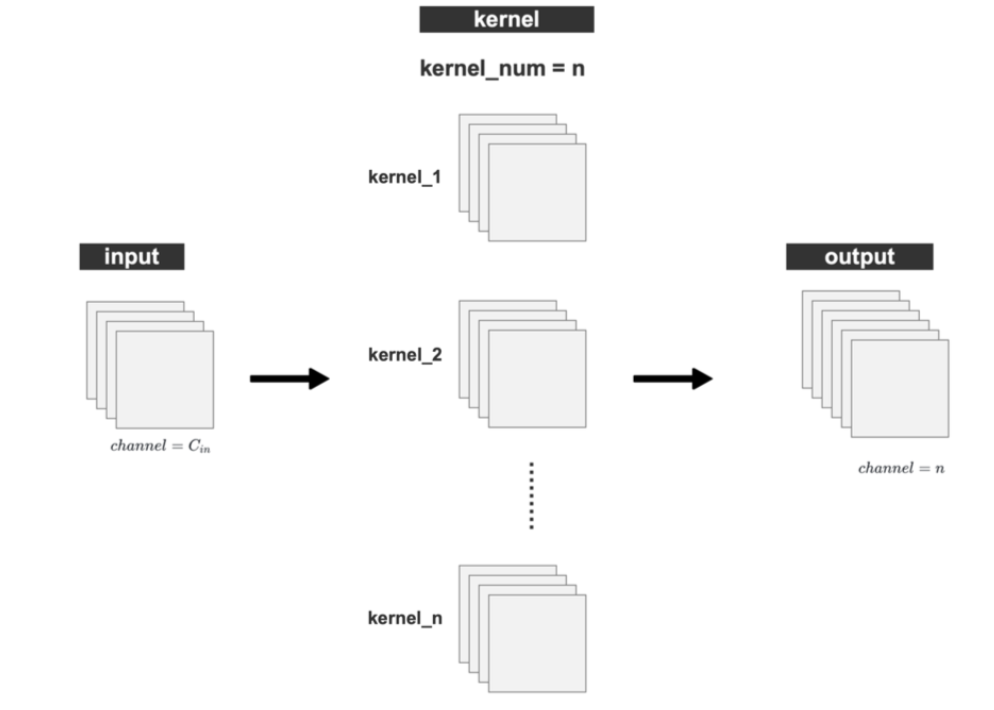
卷积通道数：

• 卷积核的数量决定输出的张量的通道数$n$，输入的张量和每一个核Kernel做卷积运算得到一个channel的输出。
• 输入通道数$C_{in}$决定每一个卷积核的通道数

卷积输出feature map的尺寸的计算公式：

• $W\_out=\frac{W_{in}+2P_w-K_w}{S_w}+1$
• $H\_out=\frac{H_{in}+2P_h-K_h}{S_h}+1$

其中，输入的尺寸为 $(W_{\text{in}},H_{\text{in}})$，卷积核的尺寸为 $(K_w,K_h)$，步幅为 $(S_w,S_h)$，填充为 $(P_w,P_h)$，输出的尺寸为 $(W_{\text{out}},H_{\text{out}})$

Group Convolution 分组卷积

Group convolution（分组卷积）最早是在AlexNet（Alex Krizhevsky等人于2012年提出的深度神经网络模型）中引入的。在 AlexNet中，作者们使用了分组卷积来将计算分布到多个GPU上。

计算

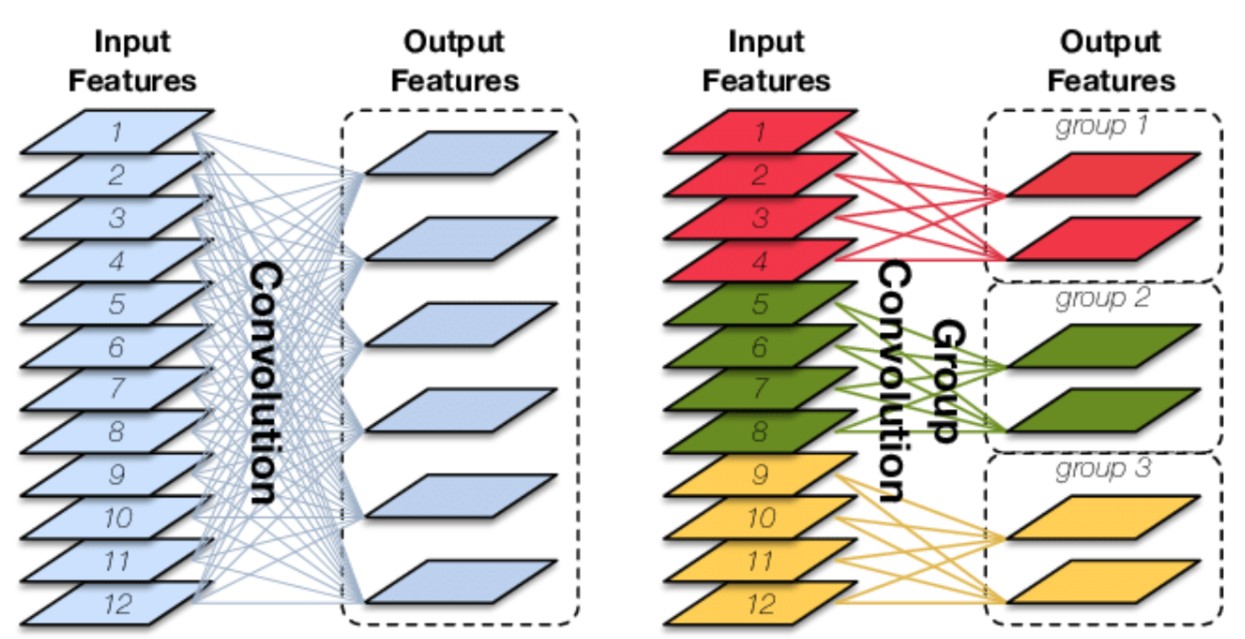
Group Convolution ：将输入的 feature map张量 在 channel 的维度上进行分组，然后再对每个分组 分别进行卷积操作，再将各个输出沿channel维度拼接在一起。

参数量

Group Convolution 优点为可减小参数量。

如下图，假设输入尺寸为 $C_{in}\times H\times W$，卷积核尺寸为 $K\times K$，输出的 Channel 数为 $n$，我们对于相同的输入和输出尺寸，分别使用 普通卷积 和 分组卷积来进行操作，并对比两种卷积方式的参数量。

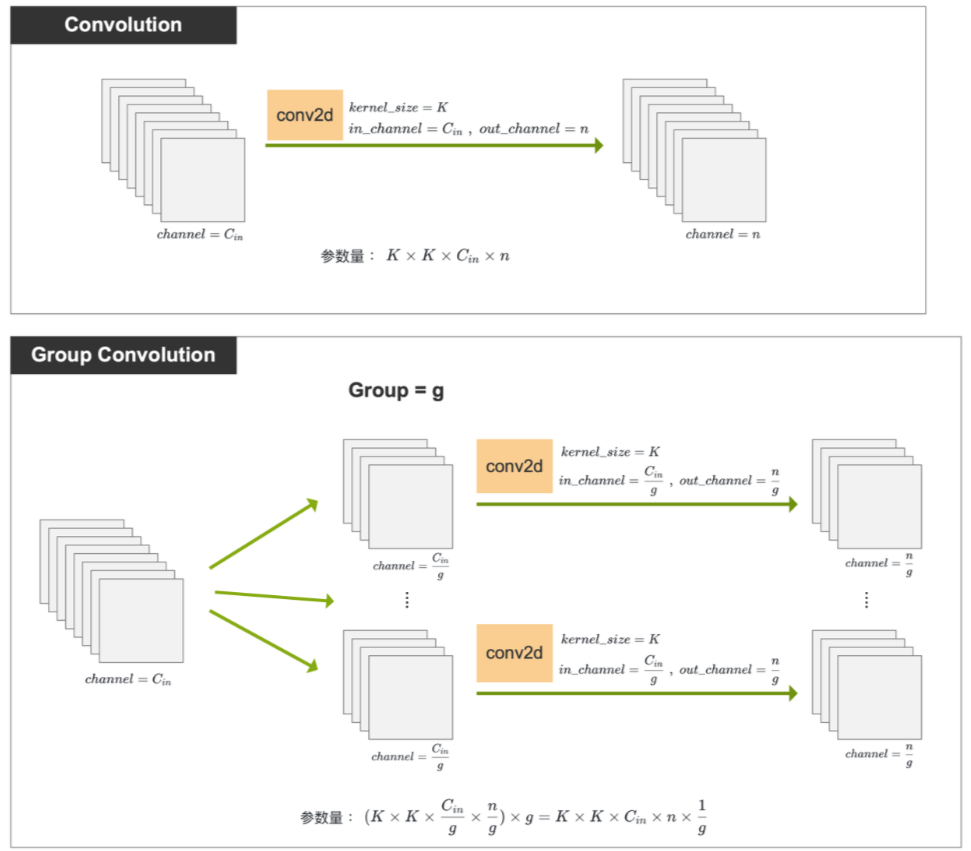
• 普通卷积：每个Kernel参数量为$K\times K\times C_{in}$ 一共有$n$个Kernel，总共参数量为：
  $$K\times K\times C_{in}\times n$$
• 分组卷积：将输入分为$g$个组，每个组进入普通卷积的channel数为 $\frac{C_{in}}{g}$，要保证最后沿channel维度拼接后为$n$，所以每个普通卷积的数维度为$\frac{n}{g}$，所以每个组用的卷积核参数量为 $K\times K\times \frac{C_{in}}{g}\times \frac{n}{g}$，一共$g$个组，所以总参数量为：
  $$(K\times K\times \frac{C_{in}}{g}\times \frac{n}{g})\times g=K\times K\times C_{in}\times \frac{n}{g}$$

所以分组卷积是普通卷积参数量的$\frac{1}{g}$。

代码实现

• 使用普通卷积方法 torch.nn.conv2d()，通过参数 groups 指定组数
• 注意：in_channels 和 out_channels 都必须可以被 groups 整除，否则会报错， 类似 ：ValueError: in_channels must be divisible by groups

import torch
import torch.nn as nnconv = nn.Conv2d(in_channels=10, out_channels=15, kernel_size=3, groups=5, stride=1, padding=1)
output = conv(torch.rand(1, 10, 20, 20))
print(output.shape)   # torch.Size([1, 15, 20, 20])

Depth-wise Convolution 逐深度卷积

是分组卷积的特例：当Group Convolution 的分组数量 $g$ 最大，等于输入channel 数$C_{in}$时，就变为了 Depth-wise Convolution逐深度卷积。

计算

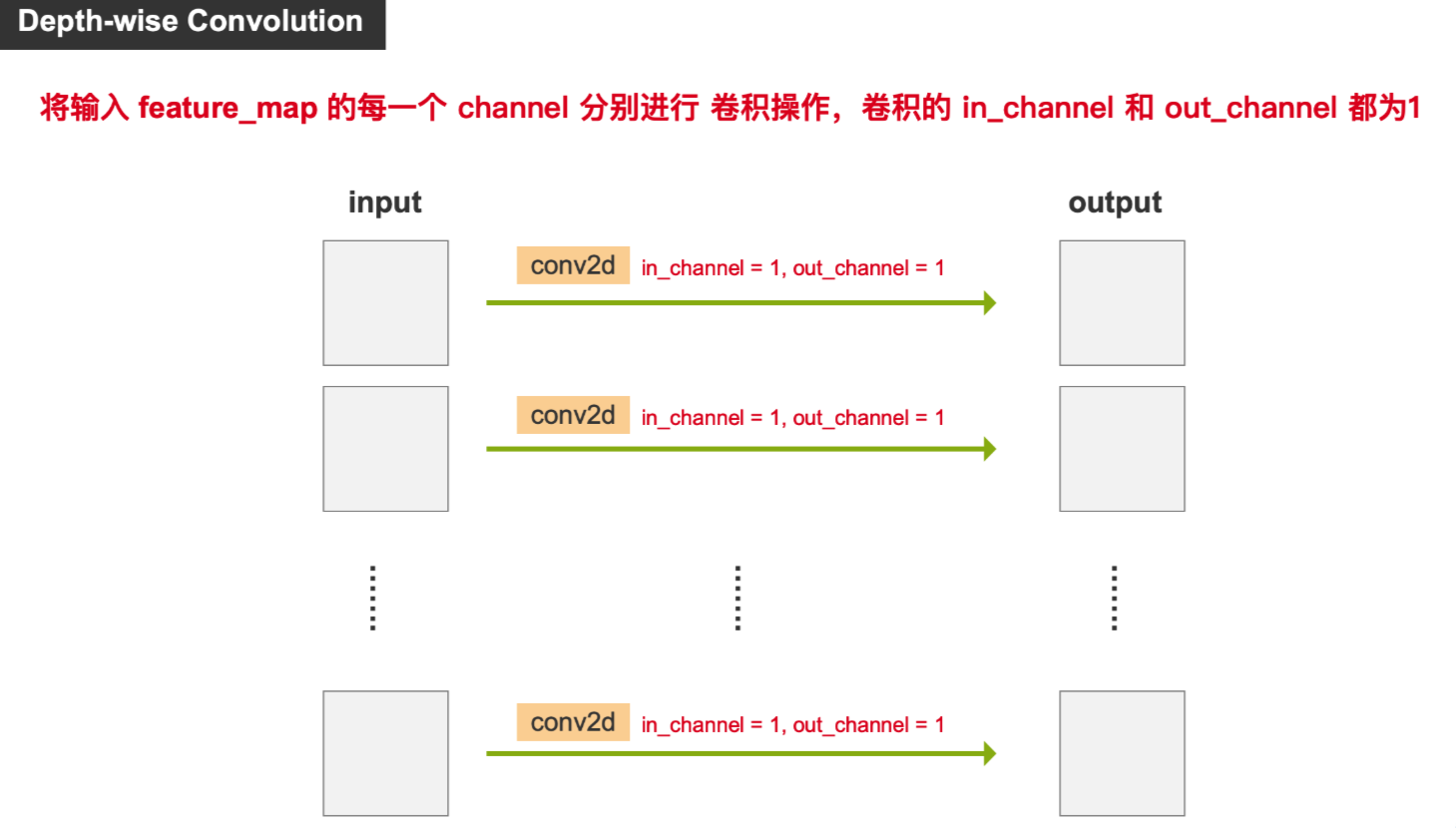
将输入的每个通道（channel）独立地进行 普通卷积运算（$C_{in}$和$C_{out}$都为1），每个通道使用一个单独的卷积核进行处理，即为 DWConvolution

具体做法如下：

• 将输入特征图按照 channel 进行分组，每个 channel 一个组，即 $g=C_{in}$
• 每个 channel （即每个 group ） 使用一个独立的卷积核（大小为 $1\times k\times k$ ）对其对应通道做卷积运算，输入输出通道均为 1

和Group Convolution的优点一样，参数量和计算量小。

代码实现

nn.Conv2d 的参数 out_channels 和 groups 都设置为等于 in_channels

import torch
import torch.nn as nnconv = nn.Conv2d(in_channels=10, out_channels=10, kernel_size=3, groups=10, stride=1, padding=1)
output = conv(torch.rand(1, 10, 20, 20))
print(output.shape)   # torch.Size([1, 10, 20, 20])

Point-wise Convolution 逐点卷积

是特殊的普通卷积，kernel_size=1x1，也就是我们经常看到的一乘一卷积 conv 1x1，
因为感受野是1x1，没有融合垂直于channl维度的平面上的信息，所以它通常用来组合每个像素各个通道之间的特征信息。

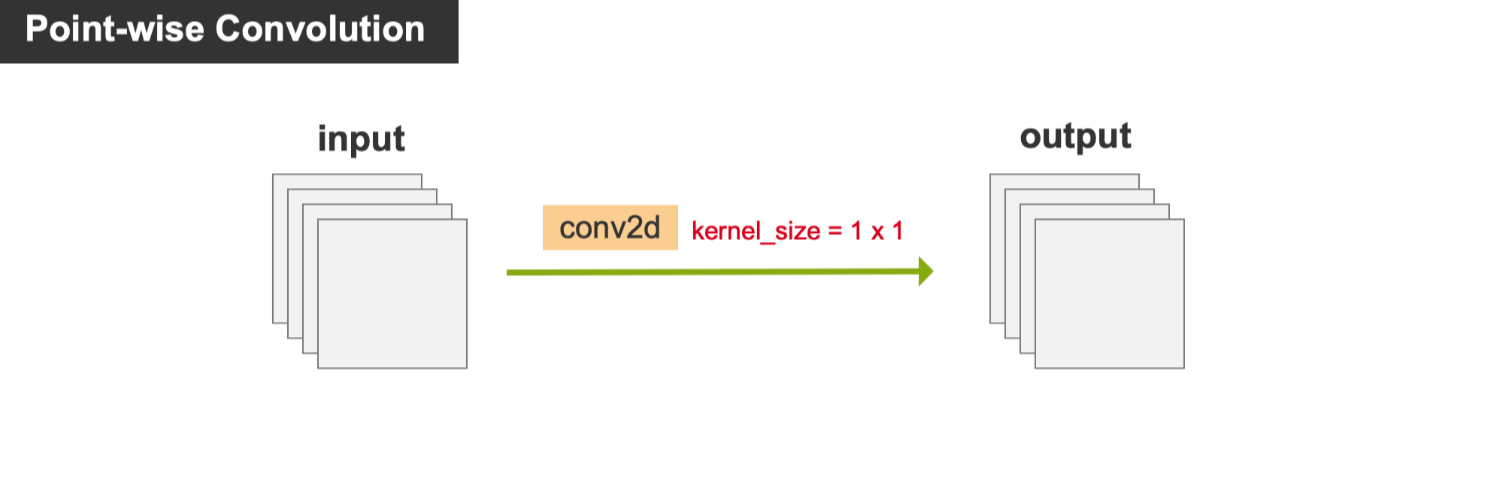
优点 ：参数量和计算量小

代码实现：将 nn.Conv2d 的参数 kernel_size 设置为等于 1

import torch
import torch.nn as nnconv = nn.Conv2d(in_channels=10, out_channels=10, kernel_size=1, stride=1)
output = conv(torch.rand(1, 10, 20, 20))
print(output.shape)   # torch.Size([1, 10, 20, 20])

Depth-wise Separable Convolution 深度可分离卷积

提出背景

Depth-wise Separable Convolution（深度可分离卷积）最早是由Google的研究团队在2014年提出的。该方法首次出现在论文《MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications》中。

计算

Depth-wise Separable Convolution 是

• 先做一个 Depth-wise Convolution ，后面再做一个 Point-wise Convolution
• 或者 先做一个 Depth-wise Convolution ，后面再做一个 Point-wise Convolution

计算量

Depth-wise Separable Convolution 的优势是 极大的减小了卷积的计算量。

这里还是对于相同的输入和输出尺寸，对比普通卷积核深度可分离卷积的计算量。
输入尺寸$D_F\times D_F\times M$，输出通道数为$N$

1、普通卷积计算量

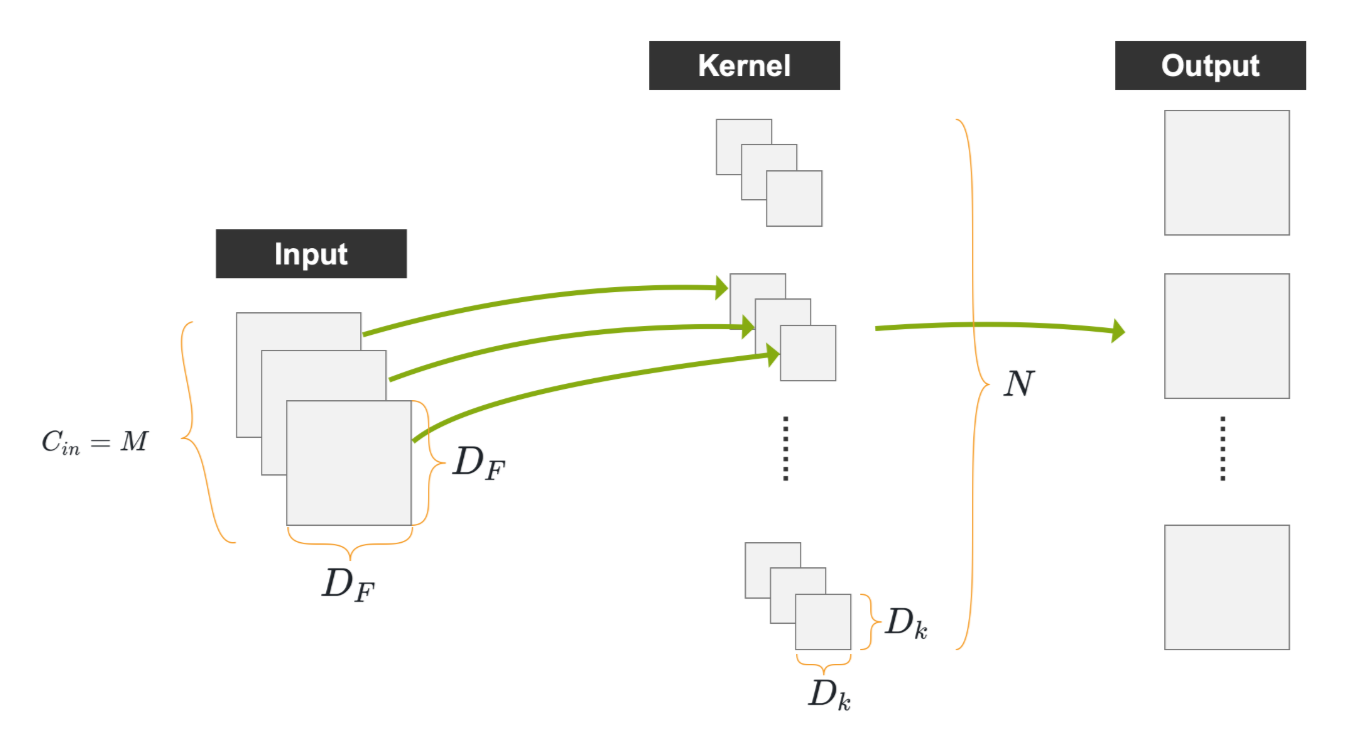
对于普通卷积，计算量公式：
$$D_k\cdot D_k\cdot M\cdot N\cdot D_F\cdot D_F\text{\hspace{1em}(1)}$$

2、深度可分离卷积（Depth-wise Separable Convolution）计算量

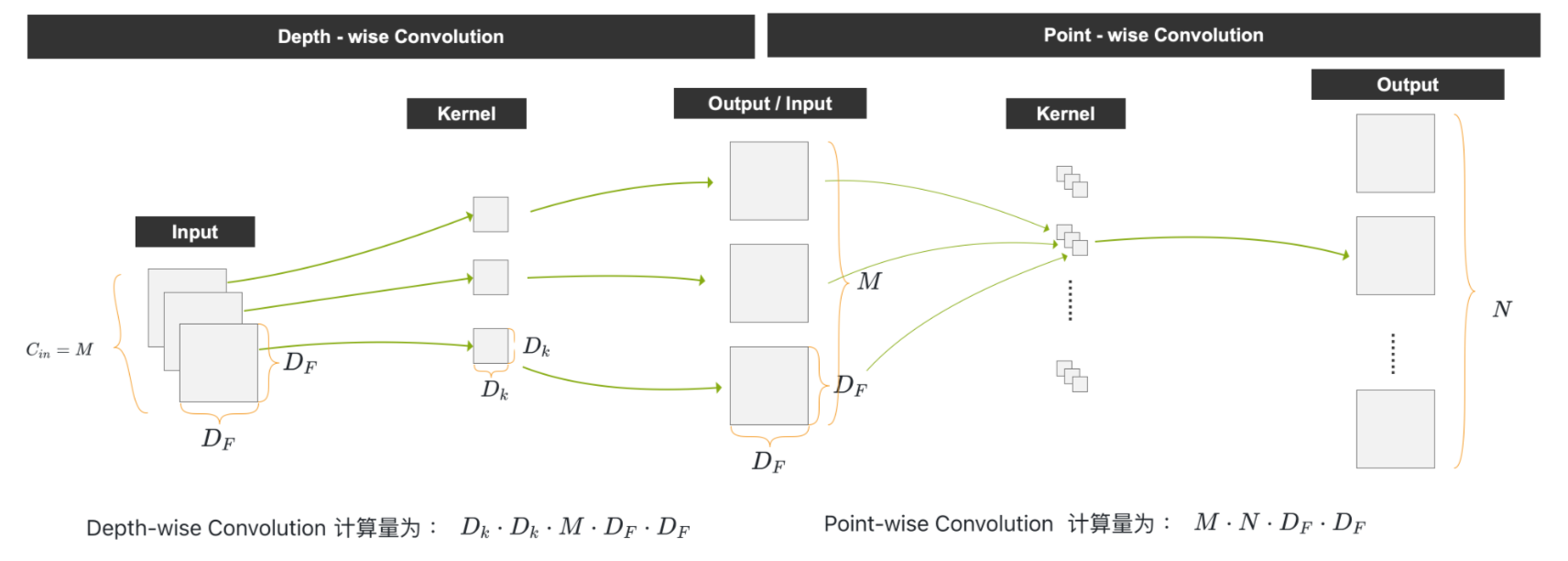
计算量分为两部分：

• Depth-wise 卷积：计算量为 $D_k\cdot D_k\cdot M\cdot D_F\cdot D_F$
• Point-wise 卷积：计算量为 $(1\cdot 1\cdot M\cdot D_F\cdot D_F)\cdot N$

深度可分离卷积计算量公式：
$$D_k\cdot D_k\cdot M\cdot D_F\cdot D_F+M\cdot N\cdot D_F\cdot D_F\text{\hspace{1em}(2)}$$

3、计算量对比（公式(2) ÷ 公式(1)）

为对比普通卷积与深度可分离卷积的计算量，用作商法比大小，将公式(2)除以公式(1)，推导得：

$$\frac{D_k\cdot D_k\cdot M\cdot D_F\cdot D_F+M\cdot N\cdot D_F\cdot D_F}{D_k\cdot D_k\cdot M\cdot N\cdot D_F\cdot D_F}=\frac{1}{N}+\frac{1}{D_k^2}\text{\hspace{1em}(3)}$$

4、典型场景（$D_k=3$，即 3×3 卷积）

实际常用 3×3 卷积（$D_k=3$ ），代入公式(3)得：

$$\frac{1}{N}+\frac{1}{D_k^2}=\frac{1}{N}+\frac{1}{9}$$

5、结论

理论上，普通卷积计算量是深度可分离卷积的 8～9 倍（因$N$为输出channel数往往很大，所以 $\frac{1}{N}$ 通常很小，主导项为 $ \frac{1}{9} $ ，故整体约为 9 倍 ）。

Dilation/Atrous Convolution 膨胀卷积/空洞卷积

计算与代码实现

• 普通卷积输出的每个像素是输入的连续的像素与卷积核运算得到的。
• 膨胀卷积输出的每个像素是输入的有间隔的像素与Kernel运算得到的。

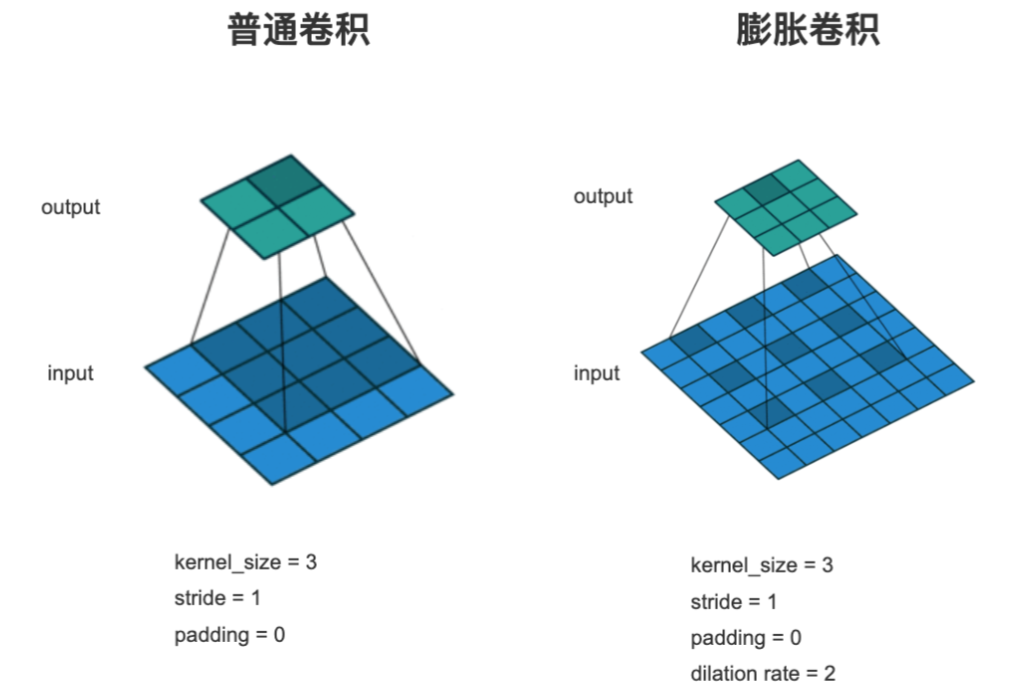
作用：增大卷积核的感受野。
感受野（Receptive Field）指CNN网络中，每个特征图的每个像素点对应输入图像的区域大小。

代码实现：指定nn.Conv2d()的膨胀率参数 dilation

• 当 dilation=1 时，没有间隔，是普通卷积
• 当 dilation=2 时，卷积核元素中间间隔一个像素

import torch
import torch.nn as nnconv = nn.Conv2d(in_channels=10, out_channels=10, kernel_size=3, stride=1, padding=2, dilation=2)
output = conv(torch.rand(1, 10, 20, 20))
print(output.shape)   # torch.Size([1, 10, 20, 20])

padding参数设置

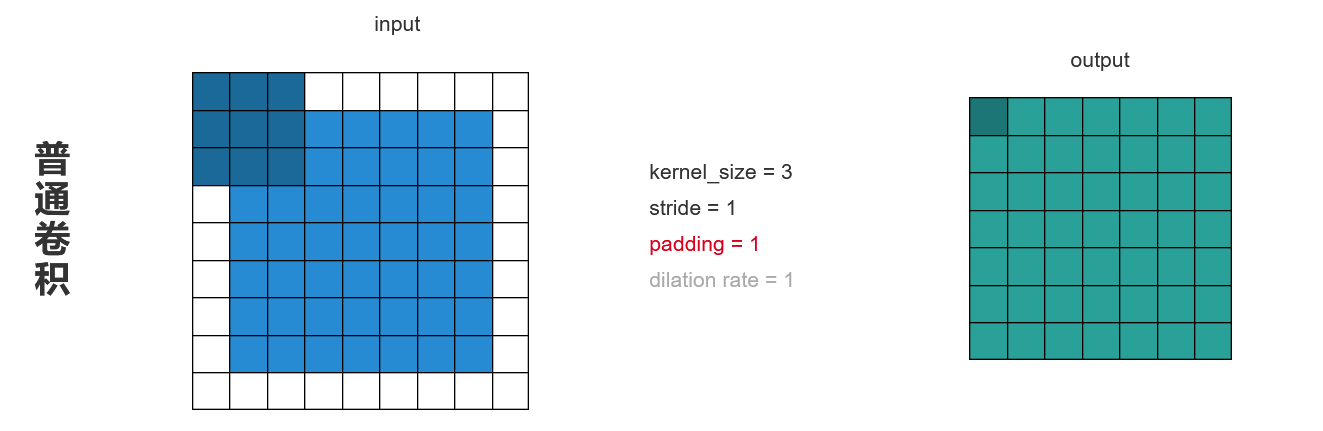
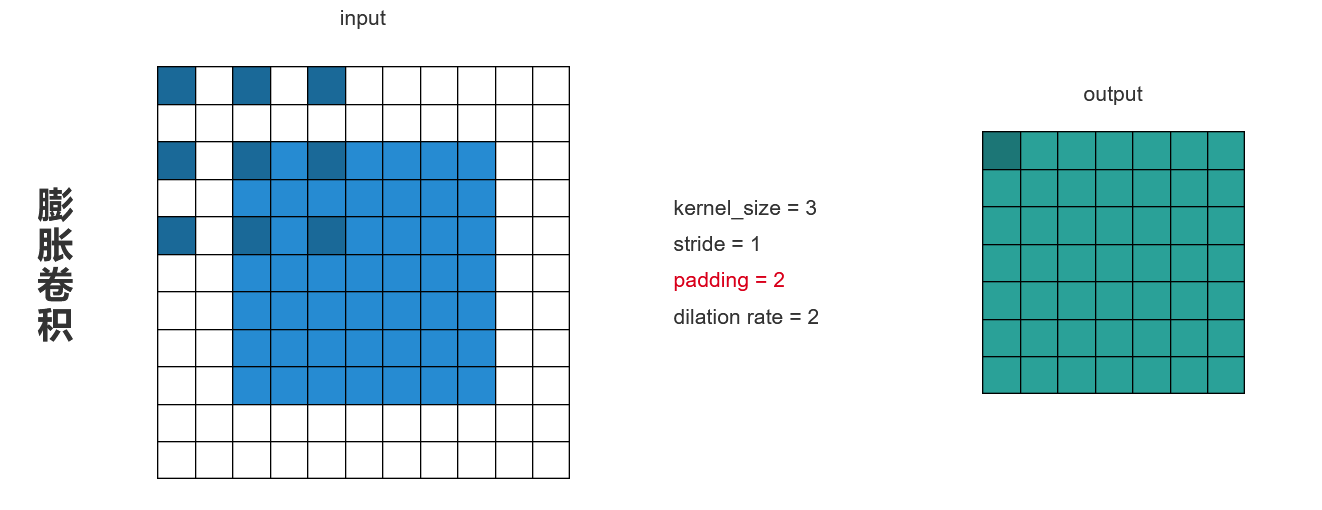
要保证输入输出的大小尺寸不变

• 普通卷积：步长stride=1，填充padding=1，即原图多加一圈像素。
• 膨胀卷积：步长stride=1，填充padding=2，加两圈像素。

缺点：网格效应Gridding Effect

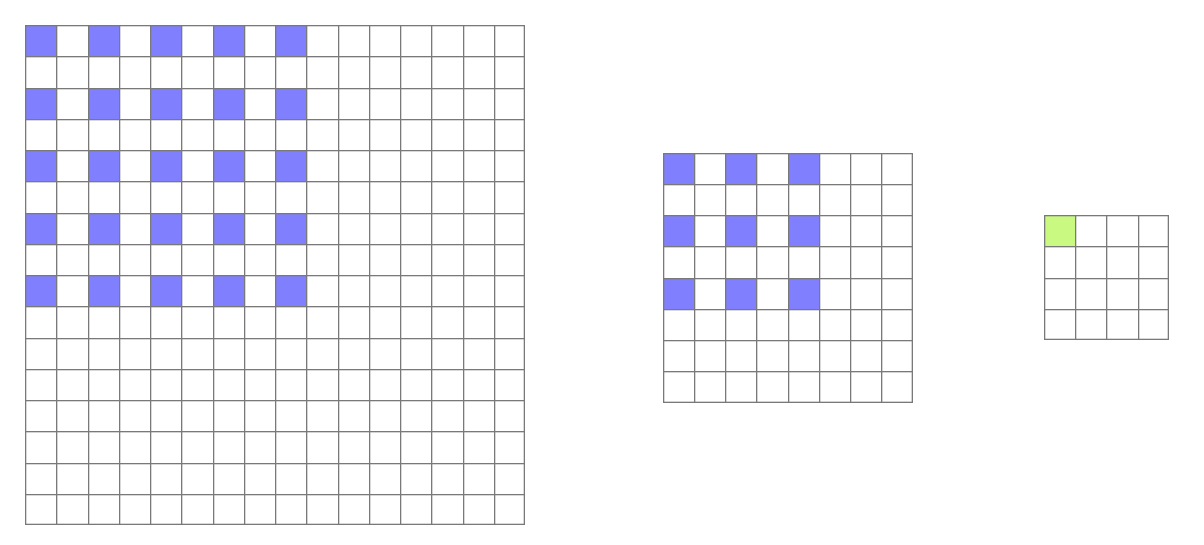
由于膨胀卷积是一种稀疏的采样方式，当多个膨胀卷积叠加时，有些像素根本没有被利用到，会损失信息的连续性与相关性，进而影响分割、检测等要求较高的任务。

比如这里连续用了两次膨胀卷积得到的feature map中的一个绿色的像素，回溯回去是由紫色像素得到的。所以如果整个网络只有两层膨胀卷积的话，相当于只有原图的四分之一的像素用到了。

Transposed Convolution 转置卷积

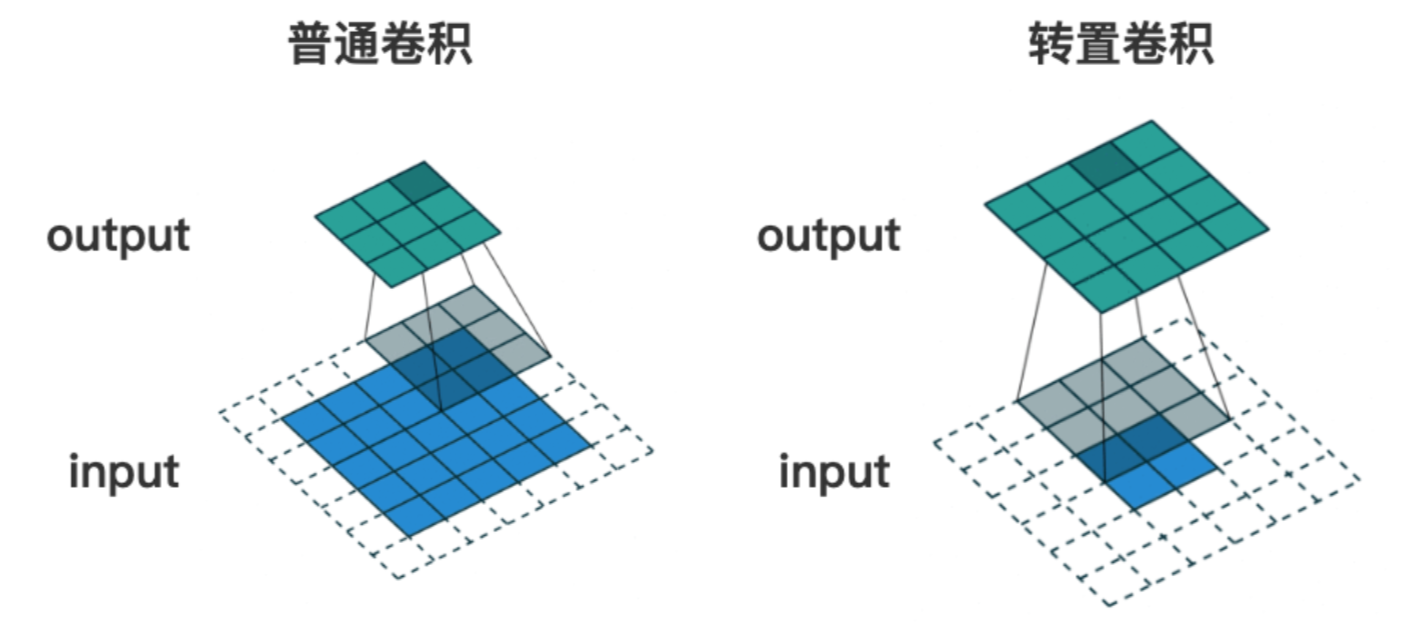
转置卷积也是卷积，只不过转置卷积 是一种上采样操作
如下图的转置卷积所示，输入图像尺寸为 2x2， 输出图像的尺寸为 4x4。

参数设置

如何设置 转置卷积 的 stride 和 padding

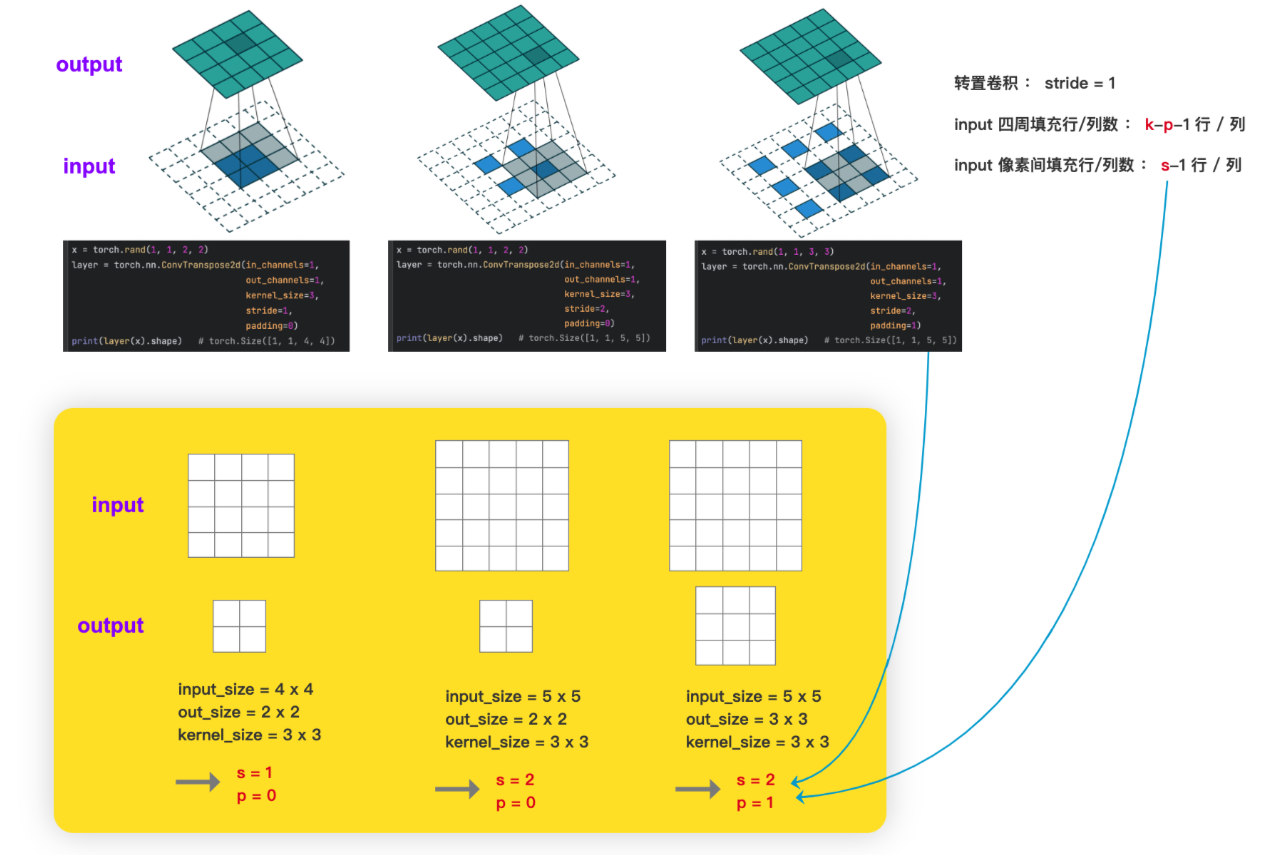
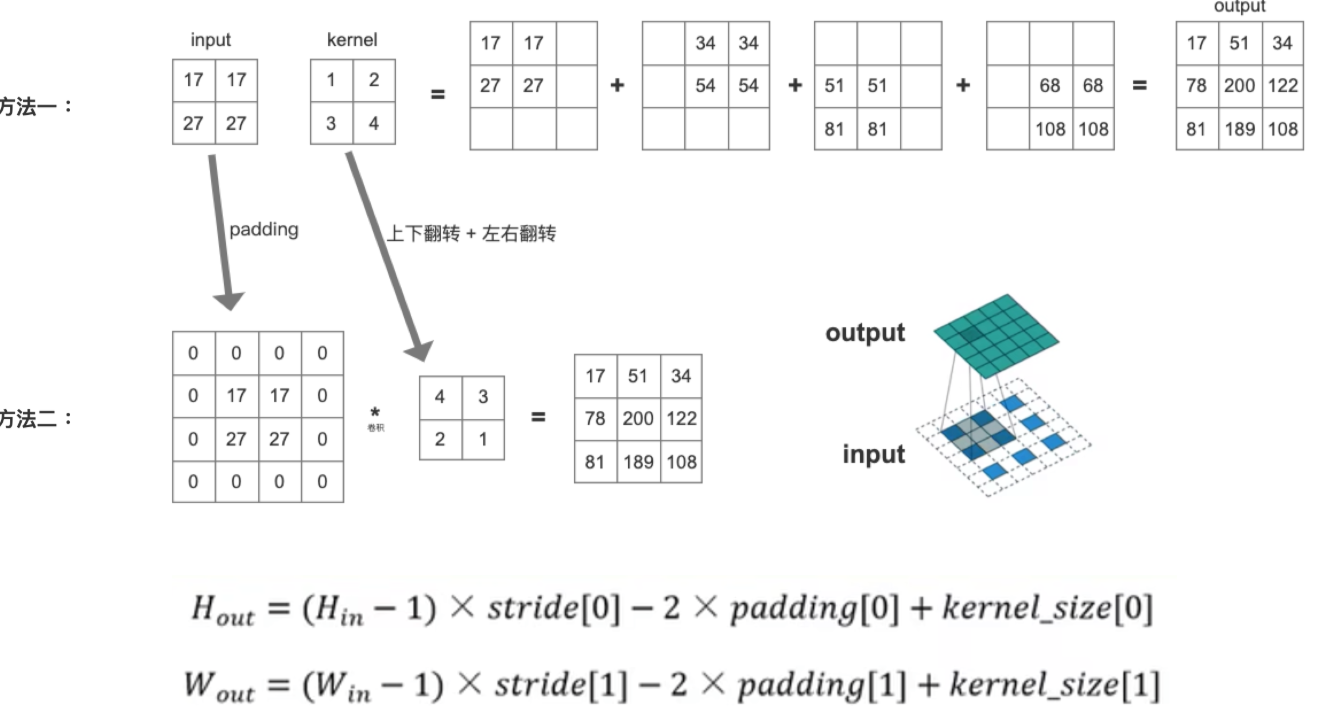
已知 input 和 kernel 求 output

Deformable Convolution 可变形卷积

论文：《Deformable Convolutional Networks》

普通卷积公式：
$$\mathbf{y}({\mathbf{p}}_0)=\sum _{{\mathbf{p}}_n\in \mathcal{R}}\mathbf{w}({\mathbf{p}}_n)\cdot \mathbf{x}({\mathbf{p}}_0+{\mathbf{p}}_n)$$

• $\mathbf{y}({\mathbf{p}}_0)$：输出特征图在位置 ${\mathbf{p}}_0$ 处的值
• $\mathbf{w}({\mathbf{p}}_{\mathbf{n}})$：卷积核（权重）在位置 ${\mathbf{p}}_{\mathbf{n}}$ 处的参数
• $\mathbf{x}({\mathbf{p}}_0+{\mathbf{p}}_{\mathbf{n}})$：输入数据在位置 ${\mathbf{p}}_0+{\mathbf{p}}_{\mathbf{n}}$ 处的原始值
• $\mathcal{R}$：卷积核的作用范围（即卷积核覆盖的所有位置集合，决定卷积的“视野”）

简单说，就是输出位置的值 = 卷积核权重与输入对应区域的加权求和。

可变性卷积公式：$$\mathbf{y}({\mathbf{p}}_0)=\sum _{{\mathbf{p}}_n\in \mathcal{R}}\mathbf{w}({\mathbf{p}}_n)\cdot \mathbf{x}({\mathbf{p}}_0+{\mathbf{p}}_n+\Delta {\mathbf{p}}_n)$$

• $\mathbf{y}({\mathbf{p}}_0)$：输出特征图在位置 ${\mathbf{p}}_0$ 处的像素值
• $\mathcal{R}$：卷积核的固定感受野范围（如 3×3 卷积的 9 个位置集合）
• $\mathbf{w}({\mathbf{p}}_n)$：卷积核在固定位置 ${\mathbf{p}}_n$ 处的权重参数
• $\mathbf{x}(\cdot )$：输入特征图
• $\Delta {\mathbf{p}}_n$：偏移量表示卷积核第 $n$ 个采样点相对于固定位置 ${\mathbf{p}}_n$ 的偏移。偏移量 $\Delta {\mathbf{p}}_n$是学习到的值，是浮点型数据，由图像经过普通卷积计算得到。