太阳平近点角详解:概念、计算与应用
1. 基本定义
**太阳平近点角(Mean Anomaly,M)**是描述天体(如地球)在其轨道上平均运动位置的角度参数。对于太阳系中的行星或卫星而言,它表示假设天体以恒定角速度运动时,从近日点开始计算的理论角度位置。
2. 轨道力学基础
在二体问题中,天体运动遵循开普勒定律:
- 开普勒第一定律:行星轨道是椭圆,太阳位于椭圆的一个焦点
- 开普勒第二定律:行星与太阳连线在相等时间内扫过相等面积
- 开普勒第三定律:轨道周期的平方与半长轴的立方成正比
3. 平近点角计算公式
3.1 基本公式
M = M₀ + n(t - t₀)
其中:
- M₀:历元时刻t₀的平近点角
- n:平均角速度(n = 2π/T,T为轨道周期)
- t:当前时刻
3.2 地球绕太阳运动的平近点角(J2000历元)
对于地球:
M = 357.52911° + 0.98560028°·d
其中d是从J2000.0起算的儒略日数
4. 相关概念对比
| 参数 | 定义 | 计算公式 | 物理意义 |
|---|---|---|---|
| 平近点角(M) | 假设匀速运动时的角度 | M = M₀ + n(t-t₀) | 理论平均位置 |
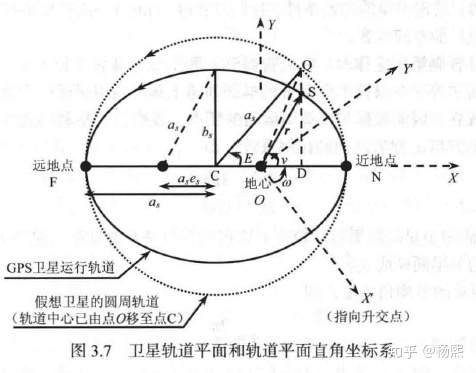
| 真近点角(ν) | 实际位置与近日点的角度 | 需解开普勒方程 | 实际观测位置 |
| 偏近点角(E) | 辅助计算用的角度 | M = E - e·sinE | 计算真近点角的中间量 |
5. 计算步骤示例
计算2023年1月1日地球的平近点角:
-
计算从J2000.0(2000年1月1日12:00 TT)到2023年1月1日0:00 UTC的日数:
- 约8400.5天
-
代入公式:
M = 357.52911° + 0.98560028°×8400.5≈ 357.52911° + 8280.5°≈ 8638.0° ≈ 358.0° (减去360°的整数倍)
6. 实际应用
6.1 轨道位置计算
通过平近点角→偏近点角→真近点角的转换,确定天体精确位置
6.2 太阳历法
用于计算太阳赤纬、日出日落时间等
6.3 航天任务
卫星轨道预报和轨道机动计算的基础参数
7. 现代计算工具
- NASA/NAIF SPICE工具包:提供精确的星历计算
- SOFA天文库:IAU标准算法实现
- VSOP87行星理论:高精度行星位置计算
8. 注意事项
- 历元选择:不同历元(如J2000、B1950)的M₀不同
- 时间系统:需统一使用TT或TDB时间
- 轨道摄动:长期计算需考虑其他天体的引力摄动
太阳平近点角作为轨道力学的基础参数,是连接理论计算与实际观测的重要桥梁,在航天工程和天文研究中具有不可替代的作用。



















