一、为什么需要 K-Means?
在监督学习中,我们总把数据写成
(x, y),让模型学习 x → y 的映射。
但现实中很多数据根本没有标签 y,例如:
啤酒:热量、钠含量、酒精度、价格
用户:访问时长、点击次数、消费金额
我们只想知道“这些样本天然能分成几类?”
这就是无监督学习——聚类。
K-Means 就是最经典、最易懂、跑得最快的聚类算法之一。
二、K-Means 的思想
随机撒 k 个“种子”当类中心,
把每个样本分给最近的种子,
再把种子移到新类的中心,
重复直到种子不再动。
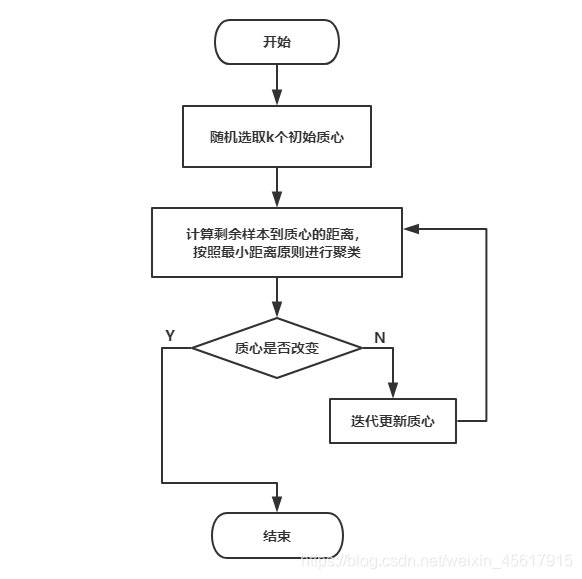
三、算法流程图解
选 k:先决定想聚几类。
初始化:随机或 k-means++ 选 k 个质心。
分配:每个样本找最近的质心,形成 k 个簇。
更新:把每个簇的均值当成新质心。
收敛:质心移动小于阈值或达到最大迭代次数。
四、Python 实战:啤酒聚类
项目目的:
在没有人工标签的情况下,把 20 种啤酒自动分成若干类别,并告诉你到底分几类最合适
1. 数据准备
我们有一份啤酒数据,只有 4 个数值特征:
表格
| 啤酒 | 热量(cal) | 钠(mg) | 酒精(%) | 价格($) |
|---|---|---|---|---|
| A | 150 | 15 | 4.5 | 2.3 |
| B | 100 | 10 | 3.0 | 1.8 |
| … | … | … | … | … |
2.读取 & 选特征
import pandas as pd
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
import matplotlib.pyplot as pltdata = pd.read_table("data.txt", sep=r'\s+', engine='python')
x = data[['calories', 'sodium', 'alcohol', 'cost']]3.选 k:轮廓系数法
轮廓系数 (Silhouette Coefficient)
对每个样本计算:
a:到同簇其它点的平均距离b:到最近外簇的平均距离s = (b - a) / max(a, b)
取值范围:
[-1, 1]≈ 1:聚得紧凑且远离它簇
≈ 0:边界模糊
< 0:可能分错了簇
用平均轮廓系数挑 k
# 1. 准备一个空列表,用来存放不同 k 值对应的轮廓系数
scores = []# 2. 依次尝试 k=2,3,...,9,看看聚成几类效果最好
for k in range(2, 10):# 2-1 用当前 k 值做 K-Means 聚类# random_state=42 保证结果可重复labels = KMeans(n_clusters=k, random_state=42).fit(x).labels_# 2-2 计算聚类结果的平均轮廓系数(-1~1,越大越紧凑)scores.append(silhouette_score(x, labels))# 3. 把 k 与对应的轮廓系数画成折线图,方便肉眼找“峰值”
plt.plot(range(2, 10), scores, marker='o')# 4. 给图加上坐标轴和标题
plt.xlabel("k") # 横轴:聚类个数
plt.ylabel("Silhouette Score") # 纵轴:平均轮廓系数
plt.title("选择最佳 k") # 图标题
plt.show() # 显示图形规则:选“峰值”对应的 k。
k=2 → 0.69 ← 最高
k=3 → 0.67
k=4 → 0.65那么 k=2 最合适。
④ 正式聚类 & 结果保存
k-means算法中的重要参数:
| 参数 | 作用 | 常用值 |
|---|---|---|
n_clusters | 类个数 | 根据业务或轮廓系数 |
init | 质心初始化 | 'k-means++'(默认)更快更稳 |
n_init | 随机初始化跑几次 | 10(默认) |
random_state | 复现实验 | 任意整数 |
best_k = 2
km = KMeans(n_clusters=best_k, init='k-means++', n_init=10, random_state=42)
data['cluster'] = km.fit_predict(x)
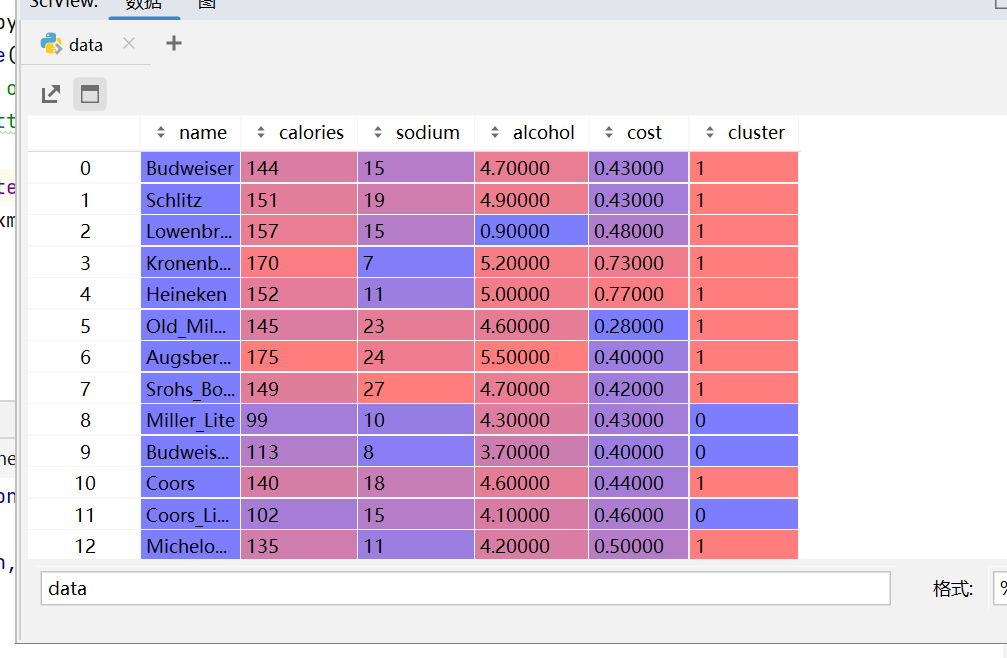
print(data.head())现在每一行都多了一个标签 cluster = 0 1,后续可以做市场细分、推荐策略等。
具体如图所示:
20种啤酒被聚类成 0,1两类
 这样的 Controller 方法)













和随机矩阵)




