笔者这些天终于达成了只狼的全成就，甚是欢喜。然而乐极生悲，最近做了些算法题，竟没有一道靠自己做出来。

感觉算法题常常用到“双指针法”呢……为什么到现在我还是做不出来这些算法题……

今天就来试着总结一下它的使用场景吧。

---

快慢指针法

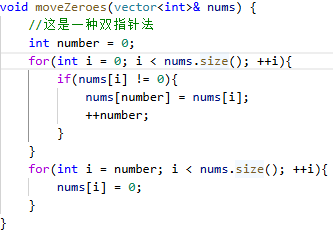
又名为“同向指针”，常见于“原地修改数组”的情况。LeetCode.283的移动零就需要通过快慢指针来实现。

题目要求将数组中所有的0移动到末尾。但是我们习惯于数组中数据前移的操作，所以我们将问题转换为“将非零数据前移并在末尾填充0”。

而快慢指针天然适用于这种场景：快指针跳过无用数据快速遍历，慢指针从头到尾依次递增方便数据覆盖。简单来说就是快指针的元素覆盖慢指针的元素。

这样一来，前移时，一个指针存放需要前移的元素（快指针），一个指针存放需要被覆盖的位置（慢指针）。最后快指针到达终点时，慢指针未遍历的元素数量就是快指针跳过的元素数量。

这里以LeetCode.80删除有序数组中的重复项为例。

不同于LeetCode.26的元素只出现一次，这里需要能够存放两个元素。那么对于这种原地修改数组的问题，我们依旧采用前指针覆盖后指针的策略。对于第26题，后指针作为被覆盖的元素，其移动受制于前指针是否发现新的不重复元素。而80题的后指针移动，不光受制于元素的不重复，也受制于后指针的前面是否够两个重复元素，如果有，就覆盖（始终从后指针的角度考虑，那些元素该保留，那些元素该被覆盖）。

class Solution {
public:int removeDuplicates(vector<int>& nums) {int x = 0;int y = 0;while(y < nums.size()){if(y <= 1){++x;}//因为元素有序，通过x-2判断同时保证了元素成功前移else if(y > 1 && nums[x-2] != nums[y]){nums[x] = nums[y];++x;}++y;}return x;}
};

相向指针法

两指针对向行驶，常见于“反转元素”的情况。LeetCode.345的反转元音字母。如果用while迭代的话，在处理完后记得让指针继续行驶。

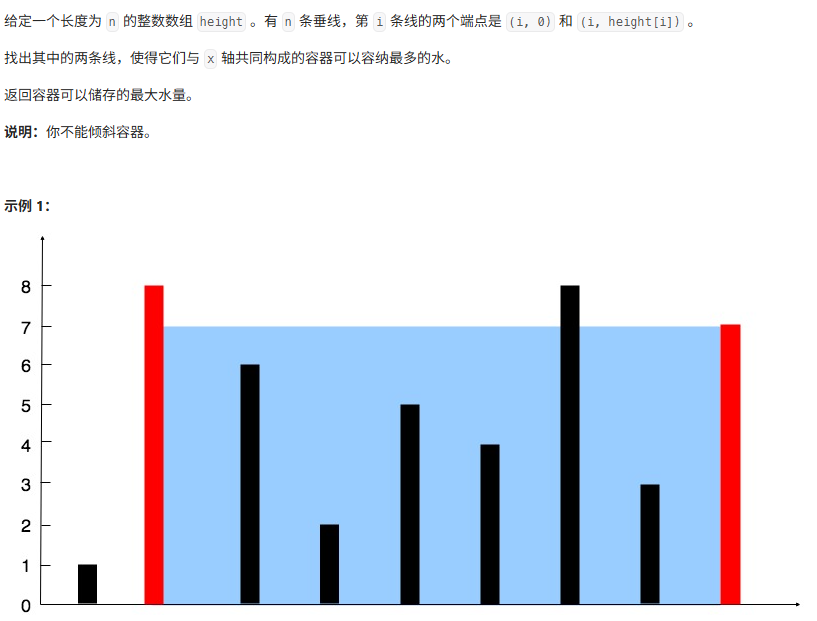
相向指针法也常常会与“贪心算法”的思想结合。常常作为条件来判断指针移动的时机。经典的是“盛水体积”问题，每次选择最短的木板移动。因为我们确定，局部的选择短板移动最终促成整体能够找到体积最大的状态（移动长板必定变小）。

这里以LeetCode.680验证回文串为例，题目要求最多删除一个字符，其能够成为回文串。这种对称的结构天然适合对向指针，只要两边一样就让两个指针行驶。

但如果两边字符不一样呢？最多删除一次的限制，我们应该考虑怎样的局部最优解能最终得出回文串。此时，若删除字符后剩余的字符串是回文串即可，那最终就是回文串。

class Solution {
public:bool validPalindrome(string s) {int left = 0;int right = s.size() - 1;bool canChange = true;while(left < right){if(s[left] == s[right]){++left;--right;}else{//两端不一样时，需要查看两种删除的情况return check(s, left + 1, right) || check(s, left, right - 1);}}//到最后就是普通回文串的情况return true;}//新建函数判断普通的回文串bool check(string s, int left, int right){for(int i = left, j = right; i < j; ++i, --j){if(s[i] != s[j]){return false;}}return true;}
};

​​​​​​​但还有一种情况是需要我们先转化之后再使用对向指针的类型。比如经典的三数之和。

如果是两数之和的话，可以直接使用双指针解开。按照这个思路，三数之和的话，固定一个数，那么剩余就是两数之和等于这个数的负数的问题。就这样继续用双指针。

class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {vector<vector<int>> vec;sort(nums.begin(), nums.end());for(int i = 0; i < nums.size() - 2 && nums[i] <= 0; i++){if(i > 0 && nums[i] == nums[i - 1]){continue;}int left = i + 1;int right = nums.size() - 1;int target = -nums[i];while(left < right){//去重if(left > i + 1 && nums[left] == nums[left - 1]){++left;continue;}int sum = nums[left] + nums[right];if(sum == target){vec.push_back({nums[i], nums[left], nums[right]});++left;--right;}else if(sum < target){++left;}else{--right;}}}return vec;}
};

​​​​​​​还有LeetCode.42的接雨水问题，这类问题的输出总是与两端元素的变化有关系，就需要考虑使用相向指针法解决。

滑动窗口

滑动窗口是一种较为特殊的同向指针，它通过两个指针来维护一个窗口，这个“窗口”通常是具有某种性质的连续元素或子串。

比较经典的就是无重复字符串的最长子串。前后指针从起点出发，前指针用于扩展窗口，并每次检测窗口“无重复字符”的性质是否改变。后指针用于收缩窗口，当字符开始出现重复，则进行收缩，当性质满足时，继续前指针扩展。这样一来，便可以遍历所有无重复字符的子串。

class Solution {
public:int lengthOfLongestSubstring(string s) {int left = 0;int right = 0;int length = 0;int maxLength = 0;vector<char> chars;bool skip = false;while(right < s.size()){char cur = s[right];for(auto c : chars){if(c == cur){//删除第一个元素chars.erase(chars.begin());++left;length = right - left;skip = true;//这里的continue对for起作用，不对while起作用break;}}if(skip){skip = false;continue;}chars.push_back(cur);++right;length = right - left;if(length > maxLength){maxLength = length;}}return maxLength;}};

​​​​​​​需要注意的是，for中的continue不对外部的while起作用。

现在以这道简单题为例，写一下滑动窗口的解法。

class Solution {
public:double findMaxAverage(vector<int>& nums, int k) {int left = 0;int right = k - 1;int sum = 0;for(int i = 0; i < k; i++){sum += nums[i];}int maxSum = sum;while(right + 1 < nums.size()){int newSum = sum - nums[left] + nums[right + 1];if(newSum > maxSum){maxSum = newSum;}            sum = newSum;++left;++right;}return (double)maxSum/k;}
};

---

小结

这便是双指针的3种常见使用方式。

如有补充交流欢迎留言，我们下次再见~