一、引言：为什么RBFN是神经网络中的“局部专家”？

在机器学习领域，神经网络的“全局逼近”与“局部逼近”一直是两大核心思路。像我们熟悉的多层感知机（MLP），使用Sigmoid、ReLU等全局激活函数，每个神经元都会对整个输入空间产生响应——就像“全员参与”处理所有数据，这种模式虽能拟合复杂函数，但训练速度慢、易陷入局部极小值。

而径向基函数神经网络（Radial Basis Function Neural Network，简称RBFN）却走出了一条“分而治之”的路：它借鉴生物神经元的“感受野”特性，让每个隐藏层神经元只对输入空间的特定局部区域响应，对区域外的数据则“漠不关心”。这种特性恰好对应一句中国俗语——“各人自扫门前雪”，每个神经元只专注处理自己“家门口”的“雪”（输入数据），再由输出层汇总所有“局部专家”的意见，最终完成任务。

这种“局部化”设计让RBFN具备三大核心优势：训练速度快（仅需线性优化输出权重）、不易陷入局部极小值（隐藏层参数通过无监督学习确定）、可解释性强（每个神经元的“责任区”清晰）。无论是实时系统（如工业控制）、非线性模式识别（如EEG脑电信号分类），还是函数逼近、时间序列预测，RBFN都能发挥重要作用。

本文将从“各人自扫门前雪”的比喻切入，系统拆解RBFN的核心思想、三层架构、数学本质、训练流程，结合可视化图表与完整Python代码，带您从理论到实战彻底掌握RBFN——即使是零基础读者，也能通过比喻和图表理解复杂概念。

二、RBFN核心思想：“各人自扫门前雪”的直观解读

要理解RBFN，首先要吃透“各人自扫门前雪”这一比喻与RBFN核心机制的对应关系。我们可以将RBFN的隐藏层神经元看作“扫雪人”，输入数据看作“雪”，每个“扫雪人”只负责自己“家门口”的一片区域，具体对应关系如下：

2.1 比喻与RBFN机制的一一对应（附可视化图）

为了更直观展示，我们用示意图呈现“扫雪人”与RBFN神经元的对应关系：

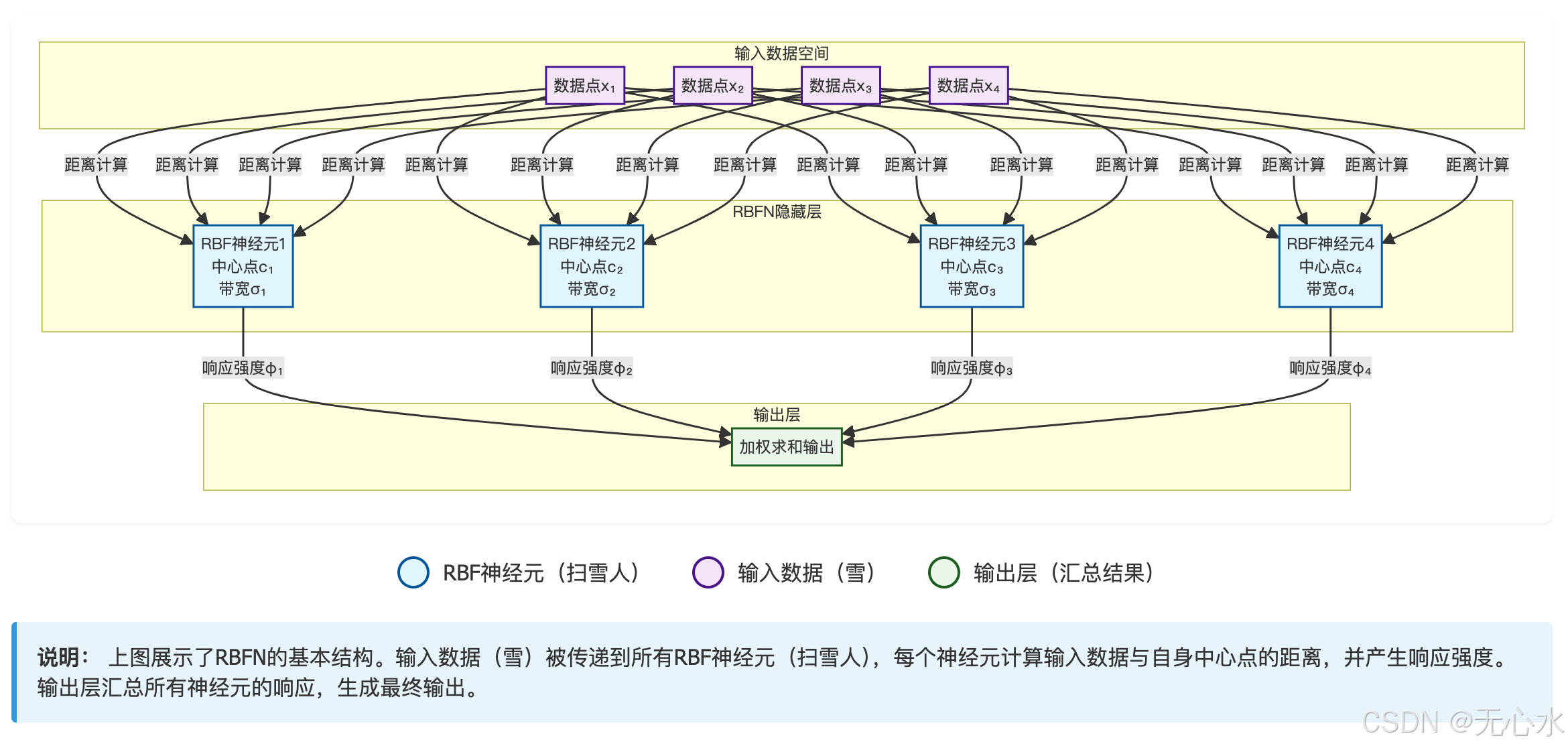
从图中可清晰看到四大对应关系：

1. “各人” → 多个RBF神经元分工
   隐藏层的每个RBF神经元都是独立的“扫雪人”，各自拥有专属的“家门口”（中心点）和“扫雪范围”（响应区域）。所有“扫雪人”共同覆盖整个输入空间，确保任何输入数据都能被至少一个“扫雪人”响应。
2. “门前雪” → RBF神经元的局部响应区域
   每个RBF神经元的“门前雪”范围由两个参数定义：
   • 中心点（${\mathbf{c}}_j$）：相当于“家门口”的位置，与输入向量维度相同（如输入是2D数据，中心点就是$(c_{j1},c_{j2})$），决定神经元最敏感的输入区域；
   • 带宽（${\sigma }_j$）：相当于“门前雪”的范围大小，控制响应区域的宽窄——带宽越大，“扫雪范围”越广；带宽越小，范围越窄。
3. “自扫” → 径向对称的局部响应
   当输入数据（“雪”）到来时，每个RBF神经元只计算“雪”到自己“家门口”（中心点）的欧氏距离（$d_j=\Vert \mathbf{x}-{\mathbf{c}}_j\Vert$），再通过径向基函数（RBF） 将距离转化为“响应强度”——这就是“自扫”的过程：
   • 若输入数据正好落在中心点（$d_j=0$），响应强度最大（接近1），如同“门前雪最厚，扫得最起劲”；
   • 随着输入数据远离中心点（$d_j$增大），响应强度指数级衰减（如高斯函数），直到趋近于0，如同“离家门越远，雪越薄，不再负责”。
4. “雪” → 输入数据与最终输出
   输入数据是需要被“处理”的“雪”，每个RBF神经元对“雪”的响应强度（激活值）会传递到输出层，输出层通过线性加权求和（权重为$w_{kj}$）汇总所有“扫雪人”的结果，最终得到网络输出——相当于“汇总各扫雪人的反馈，判断雪是否清理完成”。
   

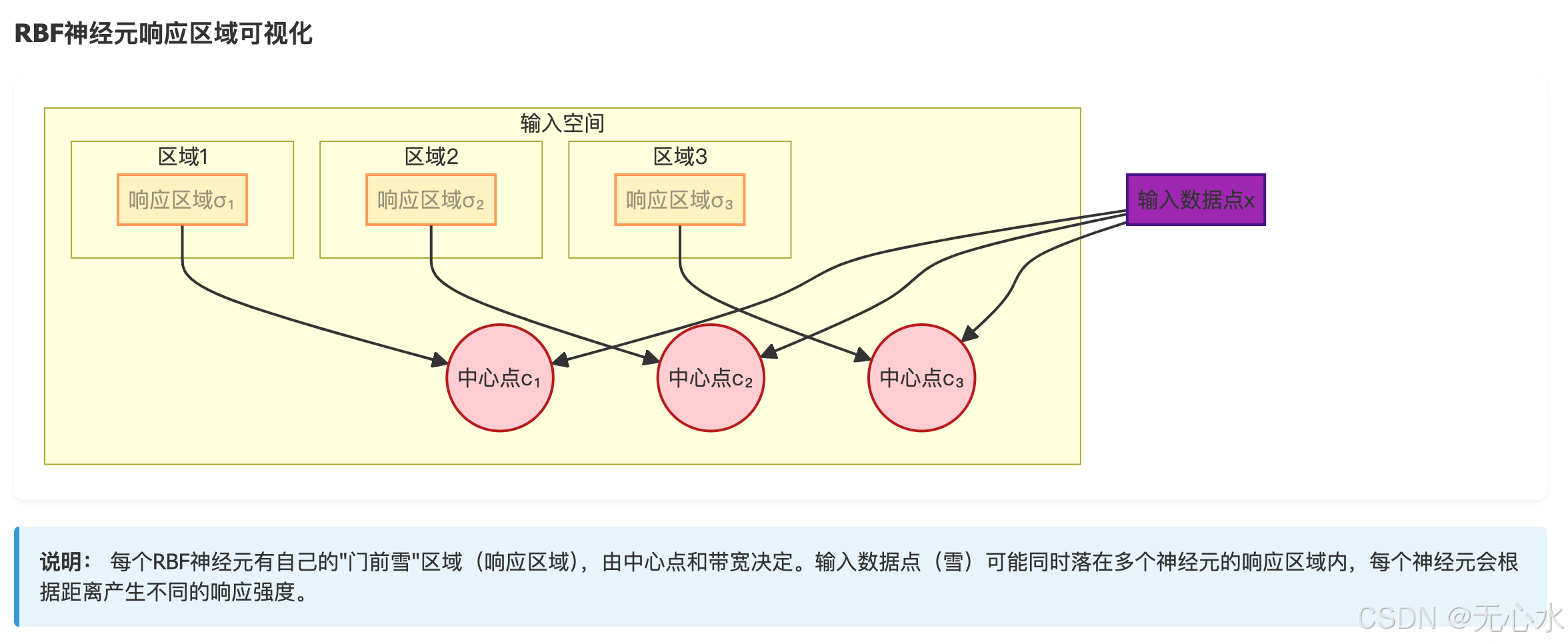
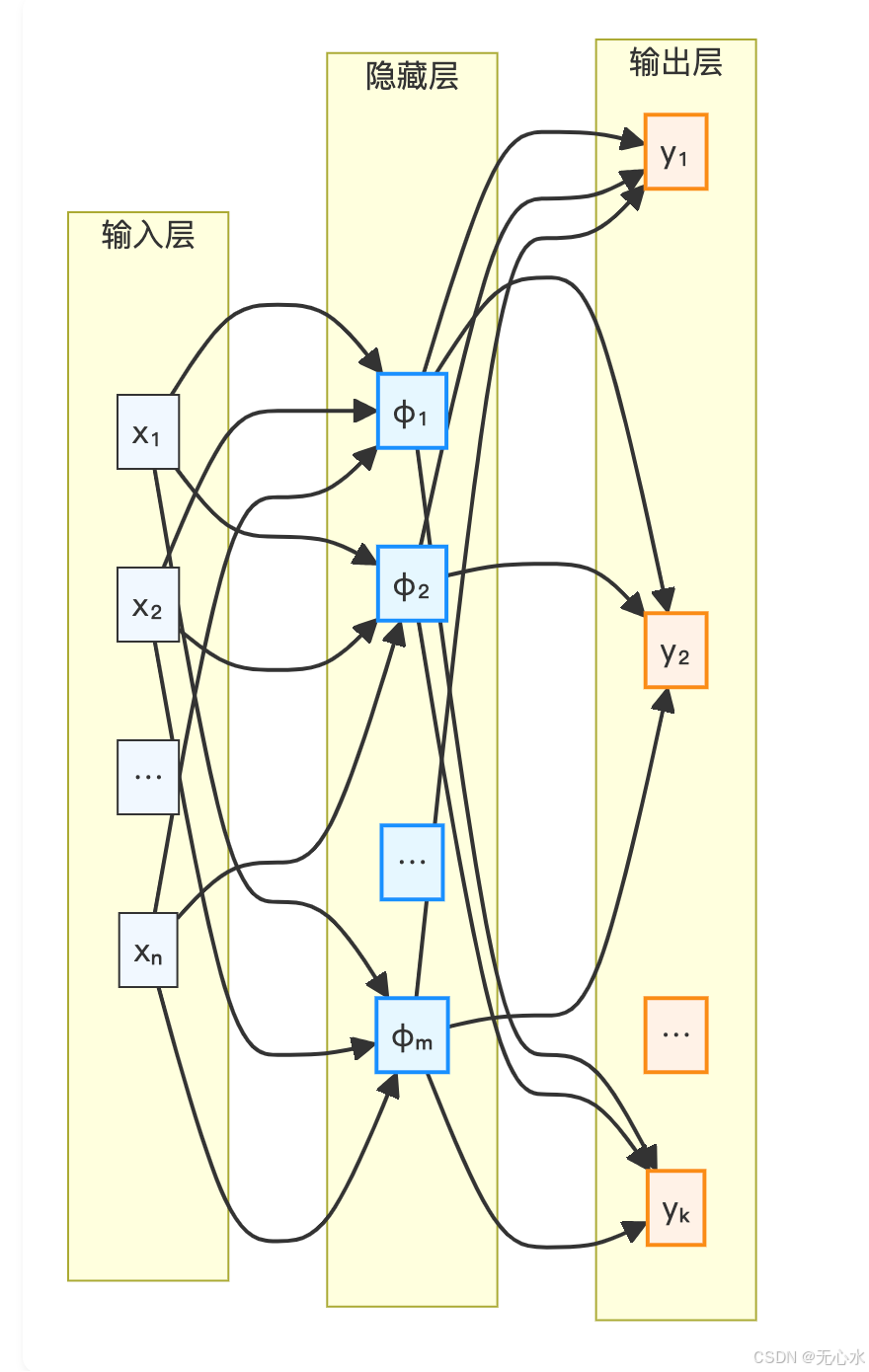
2.2 RBFN与MLP的核心差异：局部响应vs全局响应

为了突出RBFN的“局部性”，我们对比它与MLP（多层感知机）的激活函数响应模式：


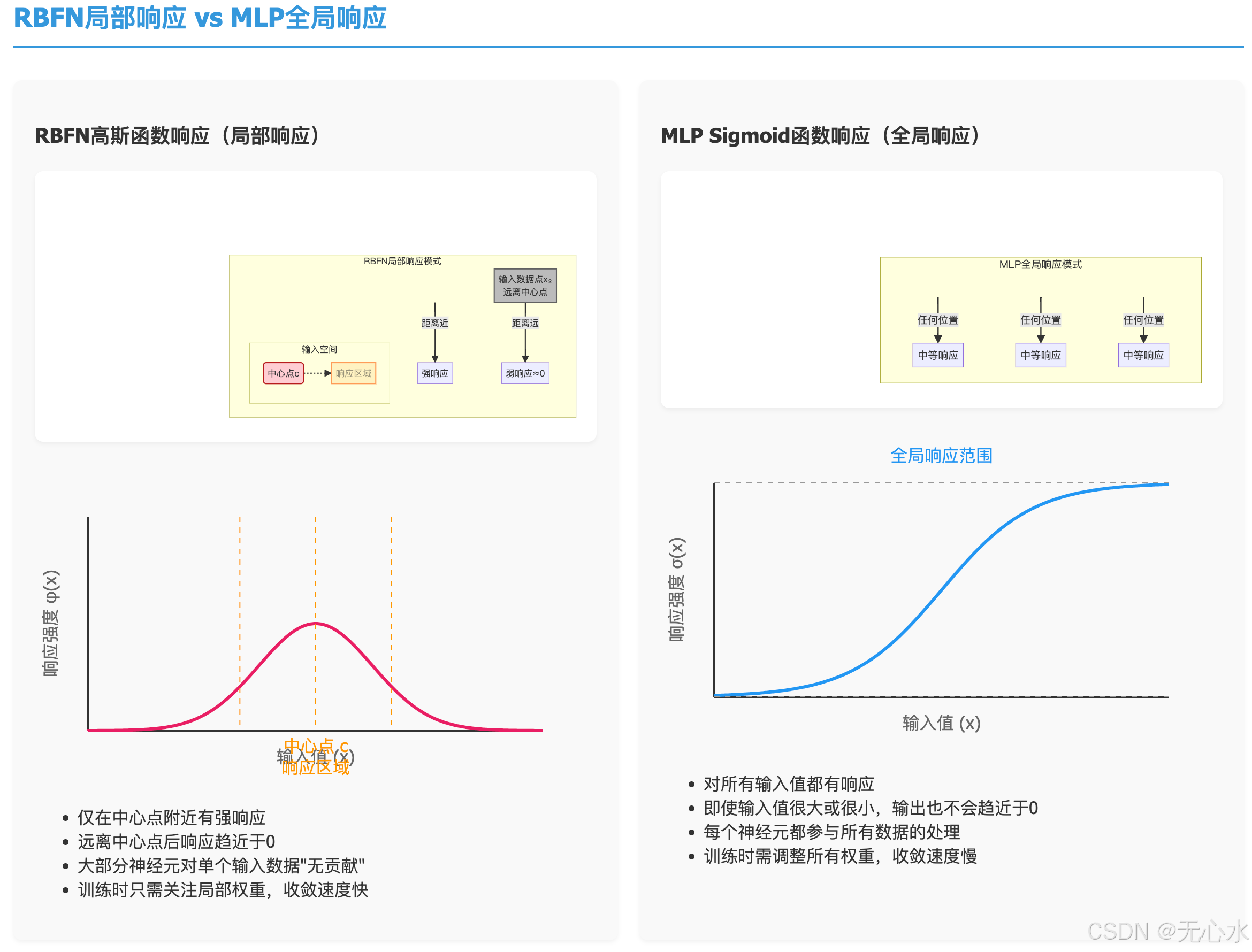
从图中可见：

• MLP的全局响应：Sigmoid函数对所有输入值都有响应（即使输入值很大或很小，输出也不会趋近于0），导致每个神经元都参与所有数据的处理，训练时需调整所有权重，收敛慢；
• RBFN的局部响应：高斯函数仅在中心点附近有显著响应，远离中心点后响应趋近于0，大部分神经元对单个输入数据“无贡献”，训练时只需关注局部权重，收敛速度远超MLP。

三、RBFN的三层架构：信号如何从输入流向输出？

RBFN是典型的三层前馈神经网络，结构简洁但功能强大。输入层接收数据，隐藏层通过RBF实现“局部响应”，输出层通过线性组合生成最终结果。我们用Mermaid流程图（图3）展示完整架构与信号流向：

3.1 三层架构可视化（Mermaid图）

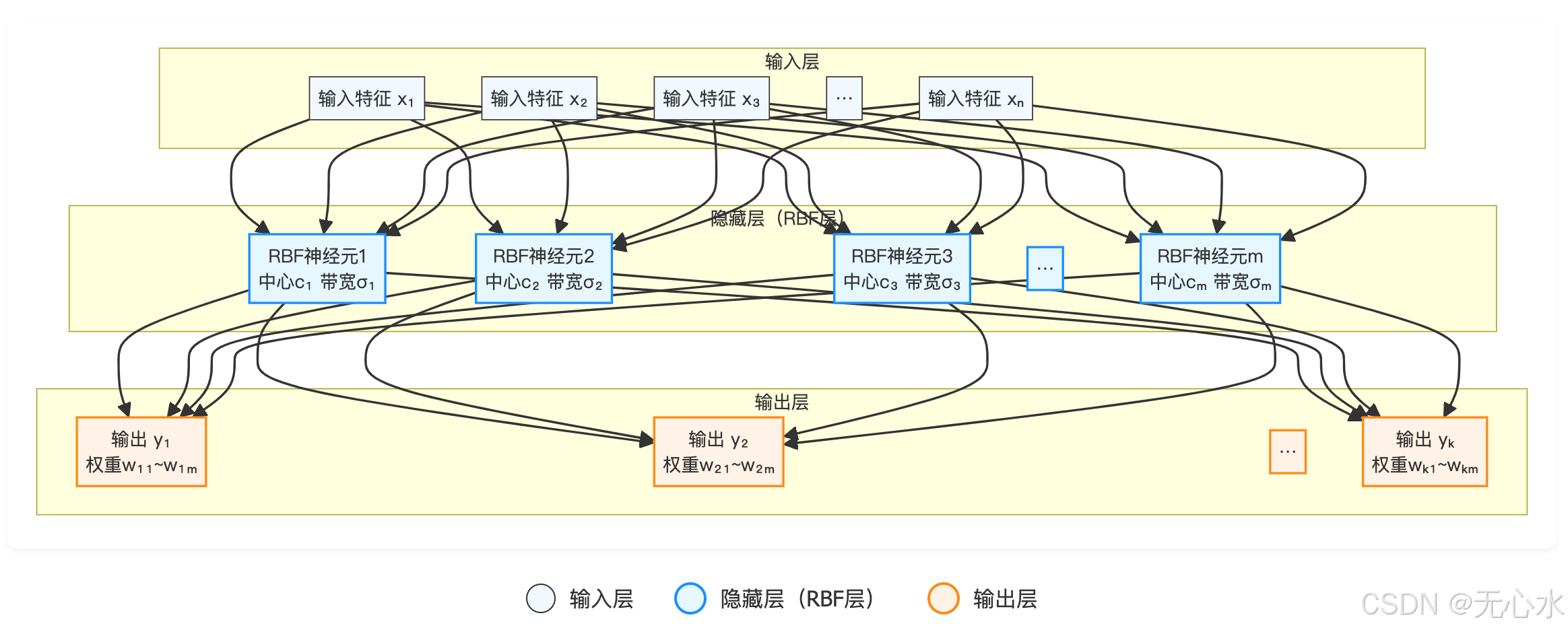
上图展示了RBFN的三层架构：输入层接收原始数据，隐藏层通过径向基函数实现局部响应，输出层通过线性加权组合生成最终结果。

3.2 各层功能详解

（1）输入层：数据“接收站”

• 功能：接收外部输入的特征向量$\mathbf{x}=(x_1,x_2,...,x_n)$，$n$为输入特征维度（如处理2D数据时$n=2$）；
• 关键特点：输入层神经元仅负责传递信号，不进行任何计算，且输入层到隐藏层的连接权重固定为1（无需训练）——这是RBFN与MLP的重要区别（MLP输入层权重需训练）。

（2）隐藏层：“局部专家”的核心阵地

隐藏层是RBFN的“灵魂”，由$m$个RBF单元组成，每个单元的核心任务是计算输入数据的“局部响应强度”，具体步骤如下（以第$j$个RBF单元为例）：

1. 计算距离：计算输入$\mathbf{x}$到自身中心点${\mathbf{c}}_j$的欧氏距离：
   $$d_j=\Vert \mathbf{x}-{\mathbf{c}}_j\Vert =\sqrt{(x_1-c_{j1}{)}^2+(x_2-c_{j2}{)}^2+...+(x_n-c_{jn}{)}^2}$$
2. 激活计算：将距离$d_j$代入径向基函数（如高斯函数），得到激活值${\varphi }_j(\mathbf{x})$（响应强度）：
   $${\varphi }_j(\mathbf{x})=\exp \left(-\frac{d_j^2}{2{\sigma }_j^2}\right)=\exp \left(-\frac{\Vert \mathbf{x}-{\mathbf{c}}_j{\Vert }^2}{2{\sigma }_j^2}\right)$$

（3）输出层：“意见汇总站”

• 功能：将隐藏层所有RBF单元的激活值${\varphi }_j(\mathbf{x})$进行线性加权求和，生成最终输出；
• 输出计算：若输出层有$k$个神经元（对应$k$个任务目标，如二分类时$k=1$，多分类时$k=$类别数），则第$k$个输出$y_k$为：
  $$y_k(\mathbf{x})=\sum _{j=1}^m{w}_{kj}\cdot {\varphi }_j(\mathbf{x})+b_k$$
  其中，$w_{kj}$是隐藏层第$j$个单元到输出层第$k$个单元的连接权重（需训练），$b_k$是输出层第$k$个单元的偏置（可选，通常可忽略）。
• 关键特点：输出层是线性层，这意味着RBFN的非线性能力完全来自隐藏层的RBF映射——通过RBF将低维非线性数据映射到高维线性可分空间，再用线性层求解。

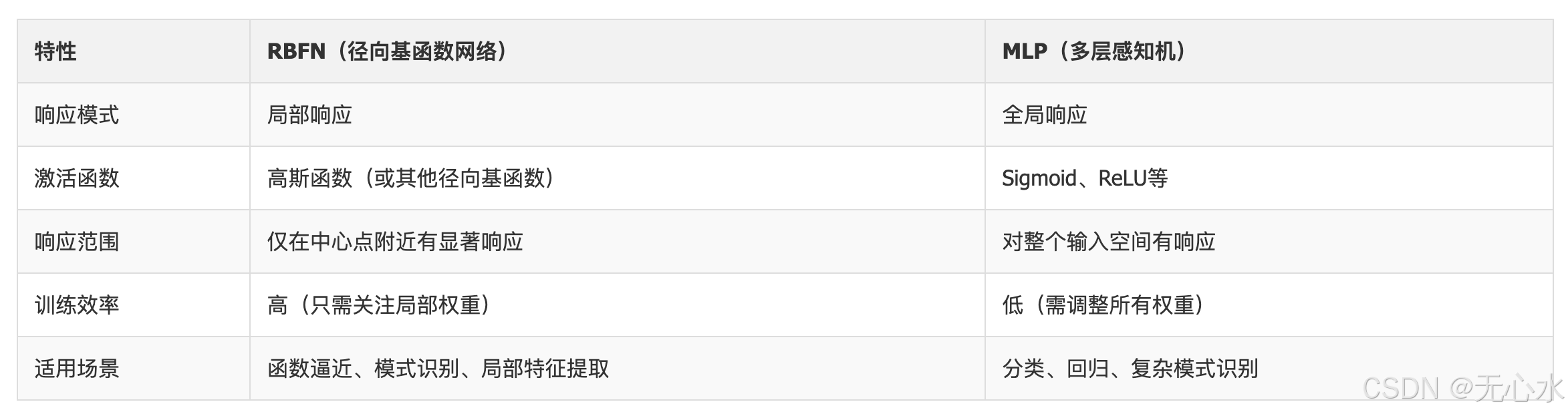
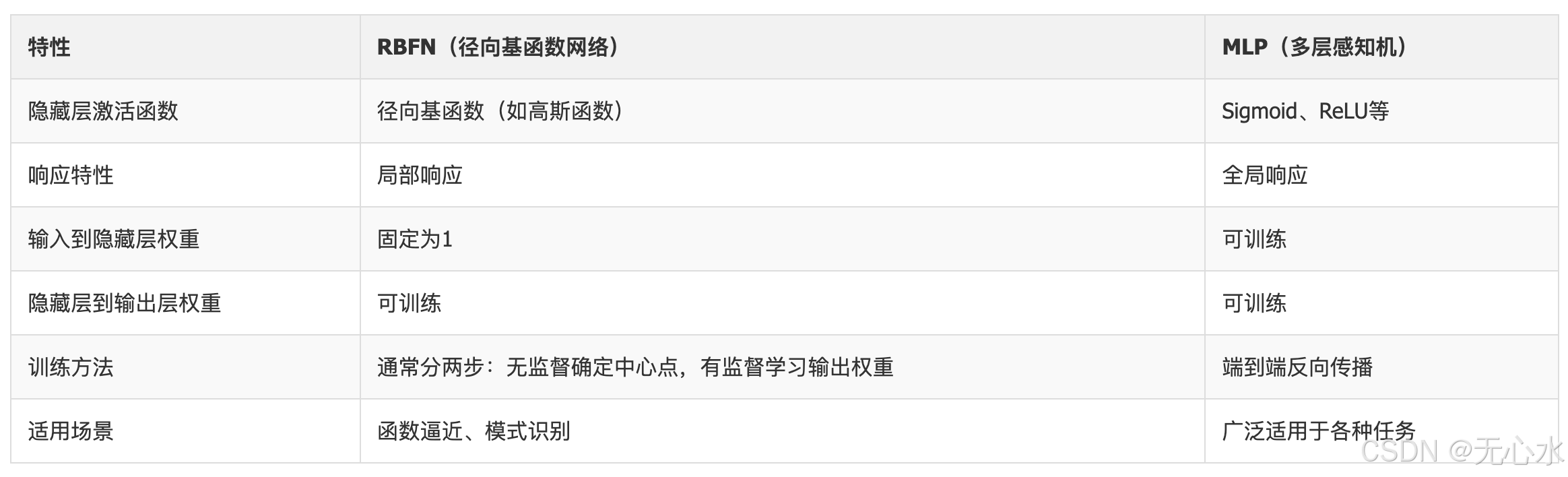
RBFN与MLP架构对比：

四、径向基函数（RBF）：RBFN的“响应核心”

径向基函数（Radial Basis Function，简称RBF）是隐藏层单元的“计算引擎”，其核心特性是径向对称——函数值仅取决于输入向量与中心点的距离，与方向无关。本节将重点讲解最常用的高斯函数，同时介绍其他常见RBF类型。

4.1 高斯函数：最常用的RBF（附可视化）

高斯函数是RBFN中应用最广泛的径向基函数，因其响应平滑、衰减快、数学性质优良，且与SVM的高斯核函数完全一致（为后续核技巧延伸奠定基础）。

（1）高斯函数的数学公式

$$\varphi (\mathbf{x},\mathbf{c},\sigma )=\exp \left(-\frac{\Vert \mathbf{x}-\mathbf{c}{\Vert }^2}{2{\sigma }^2}\right)$$
其中：

• $\mathbf{x}$：输入向量（维度为$n$）；
• $\mathbf{c}$：中心点向量（与$\mathbf{x}$同维度，决定函数的“峰值位置”）；
• $\sigma$：带宽（控制函数的“宽度”， σ > 0 \sigma>0