目录
一、先搞懂:原理图的 “构成密码”
(1)连接线:别被 “直线” 骗了!
(2)结点:红色小圆点才是 “真・连接”
(3)网络标签:“无形的连线”
二、必掌握:“支路、回路、网孔” 的概念辨析
(1)支路:“同一电流的通道”
(2)回路:“闭合的电流环路”
(3)网孔:“最简版回路”
三、核心定理:基尔霍夫定律,电路分析的 “万能钥匙”
(1)集总参数电路:定理的 “适用前提”
(2)基尔霍夫电流定律(KCL):“电荷不能凭空消失”
(3)基尔霍夫电压定律(KVL):“能量不能凭空产生”
四、定理小结:KCL 和 KVL 的 “配合打法”
电子电路就像一座精密的 “信号迷宫”,原理图是迷宫的 “设计蓝图”,而基尔霍夫定律是破解迷宫的 “万能钥匙”。今天咱们从原理图构成到核心电路定理,一步步把电路分析的基础逻辑讲透。
一、先搞懂:原理图的 “构成密码”
画原理图不是随便摆元件、连线条,每个元素都藏着 “潜规则”。
(1)连接线:别被 “直线” 骗了!
原理图里的绿色线条,看着是根普通导线,但实际在 PCB(印刷电路板)上是铜箔条 / 铜箔块—— 形状可能扭扭曲曲,和原理图里的直线完全不是一回事。比如电源走线为了避开其他元件,PCB 上的铜箔可能绕个大弯,而原理图里只用一条线简化表示。这是原理图与实际电路板的核心区别之一。
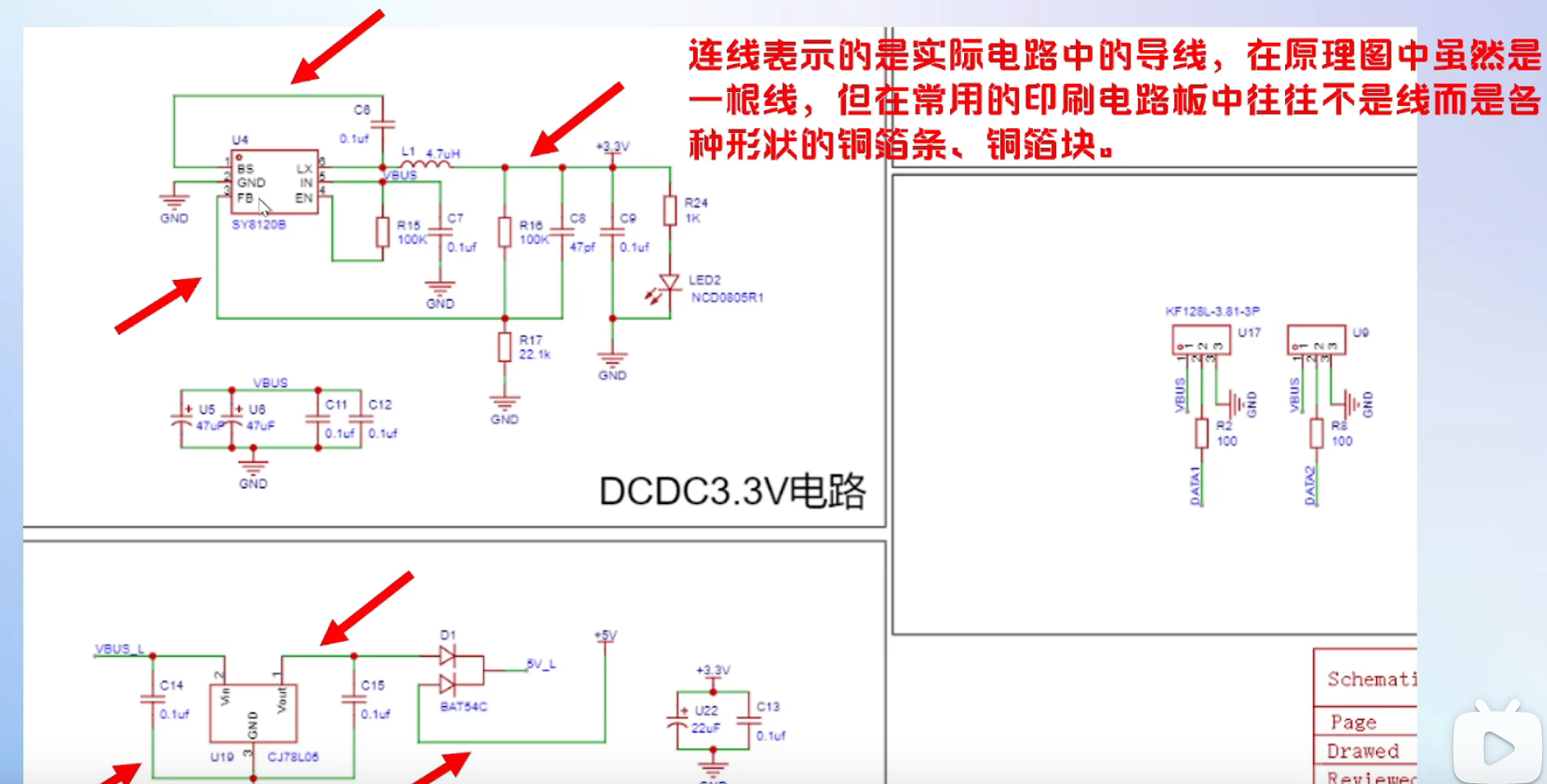

(2)结点:红色小圆点才是 “真・连接”
原理图里的红色圆点,是 “电气连接点” 的标志 —— 所有连到这个圆点的导线、元件引脚,必须保持导通。
注意:仅视觉交叉的导线,不算电气连接!就像城市里的立交桥,两条路看着交叉,实际是上下分层、互不连通的。判断结点的关键:有没有红色标记点。
举个例子:下图中多条线看似交叉,但只有带红点的 2 处,才是有效结点。
(3)网络标签:“无形的连线”
网络标签是个 “偷懒神器”——相同标签的器件,会自动建立电气连接,不用画一堆线把图搞得像 “盘丝洞”。
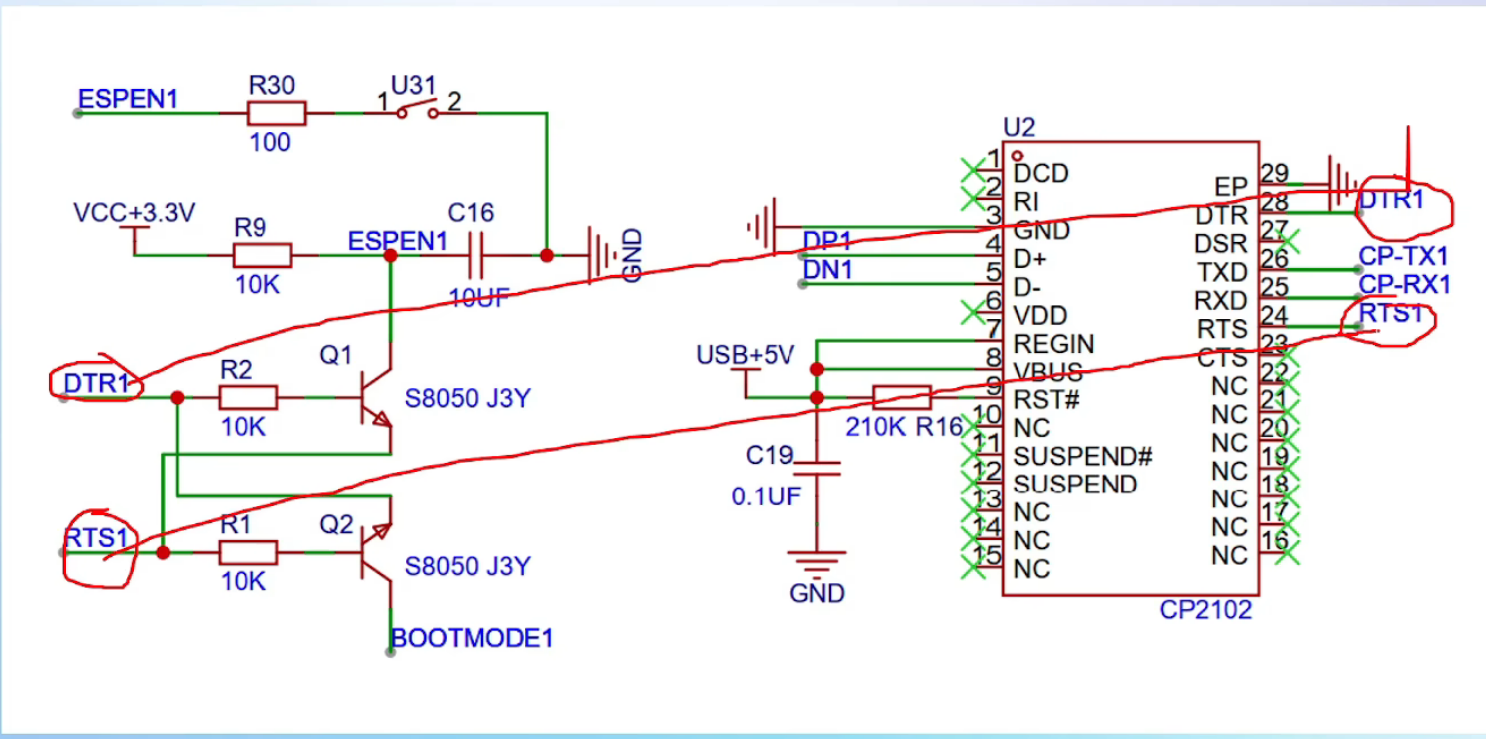
比如电源网络标VCC,所有标VCC的引脚都默认接同一电源;通信信号标UART_TX,相关模块就通过这个标签 “隐性连通”。既简化了布线,又能通过 “功能命名” 直观知道信号用途(比如DTR是串口通信信号)。
二、必掌握:“支路、回路、网孔” 的概念辨析
这三个词是电路分析的 “基础词汇”,得先分清逻辑。
(1)支路:“同一电流的通道”
电路中,通过同一电流的独立分支就是支路。它可以是单个元件(如一个电阻),也可以是多个元件串联(如 “电阻 + 二极管” 串联)。
识别方法:两个节点之间,每一条 “独立路径” 就是一条支路。同一支路里的所有元件,电流完全相同。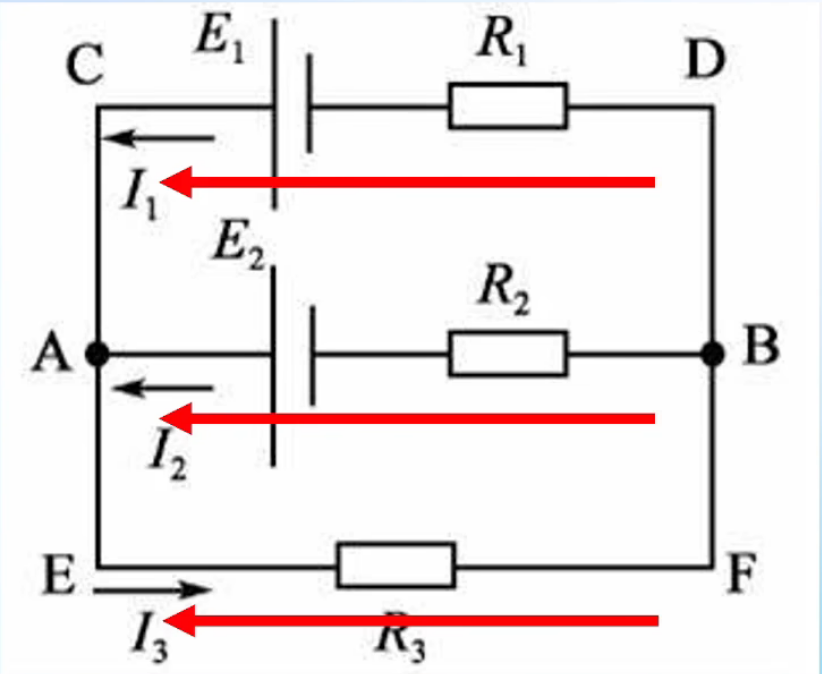
(2)回路:“闭合的电流环路”
任意闭合的电流路径就是回路(比如从电源正极出发,绕一圈回到负极)。
“独立回路” 的核心是:每次选择的回路,必须包含新的支路(类比数学里的 “独立方程”,不能重复)。如果电路没有回路,电流根本流不起来,就像 “死胡同”。
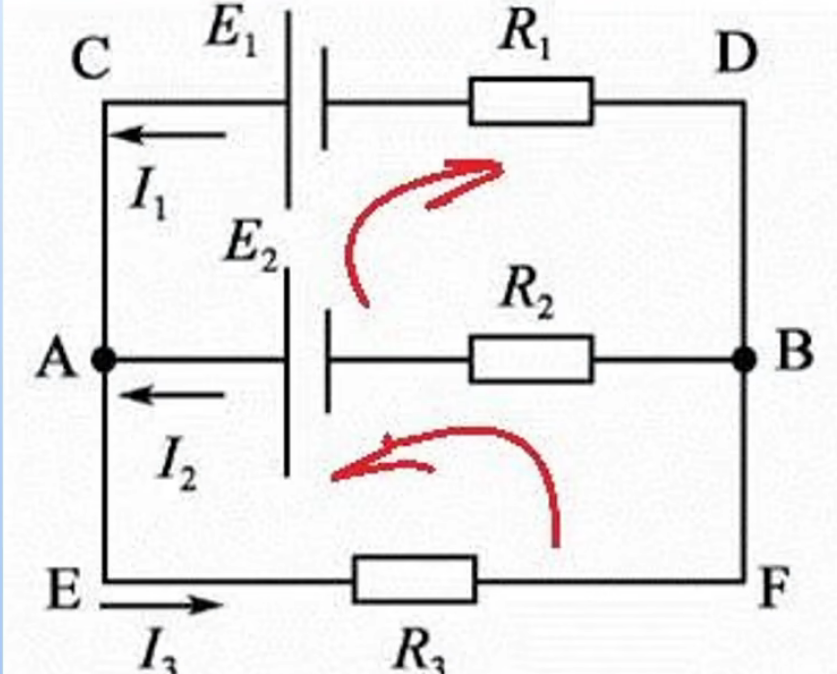
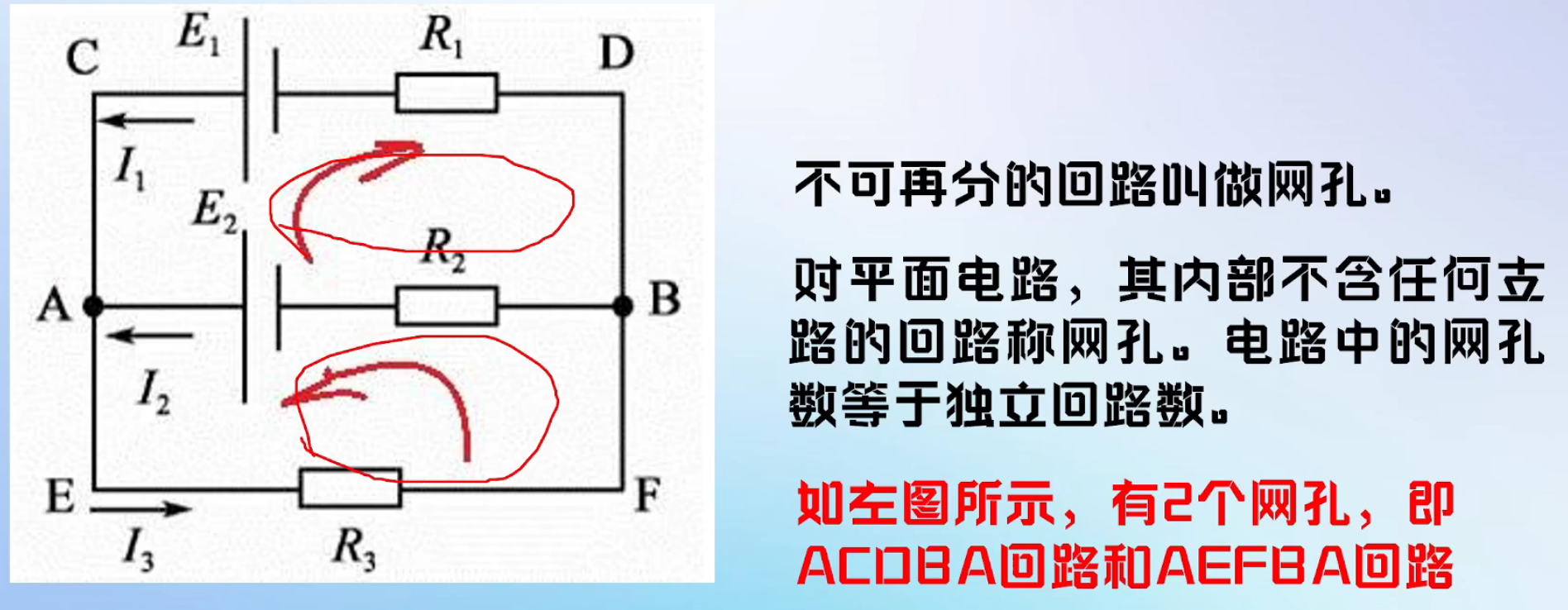
(3)网孔:“最简版回路”
网孔是内部不含任何支路的 “最简回路”。可以想象成 “渔网的孔洞”—— 中间没有其他线穿过。
平面电路里,数网孔就像数 “渔网有多少个洞”;立体电路则看 “能不能再拆分出支路”。网孔的数量等于电路的 “独立回路数”,用 “网孔法” 分析电路,能列出最简洁的方程组。
三、核心定理:基尔霍夫定律,电路分析的 “万能钥匙”
基尔霍夫定律分电流定律(KCL)和电压定律(KVL),是分析电路的核心逻辑。
(1)集总参数电路:定理的 “适用前提”
实际元件(如电阻、电容)工作时,电能消耗、电磁能储存是 “交织在整个元件里” 的。为了方便分析,我们把实际元件用 “理想元件组合” 代替(比如低频时,电阻等效为 “电阻 + 电感串联”;高频时,再并联电容)。
这种 “假设电磁现象只在元件内部发生、互不干扰” 的模型,叫集总参数电路。
但有个前提:电路尺寸必须远小于电磁波波长(公式:电路尺寸,其中c是光速,f是信号频率)。高频电路(如微波电路)波长太短,就不适用这一模型了。
(2)基尔霍夫电流定律(KCL):“电荷不能凭空消失”
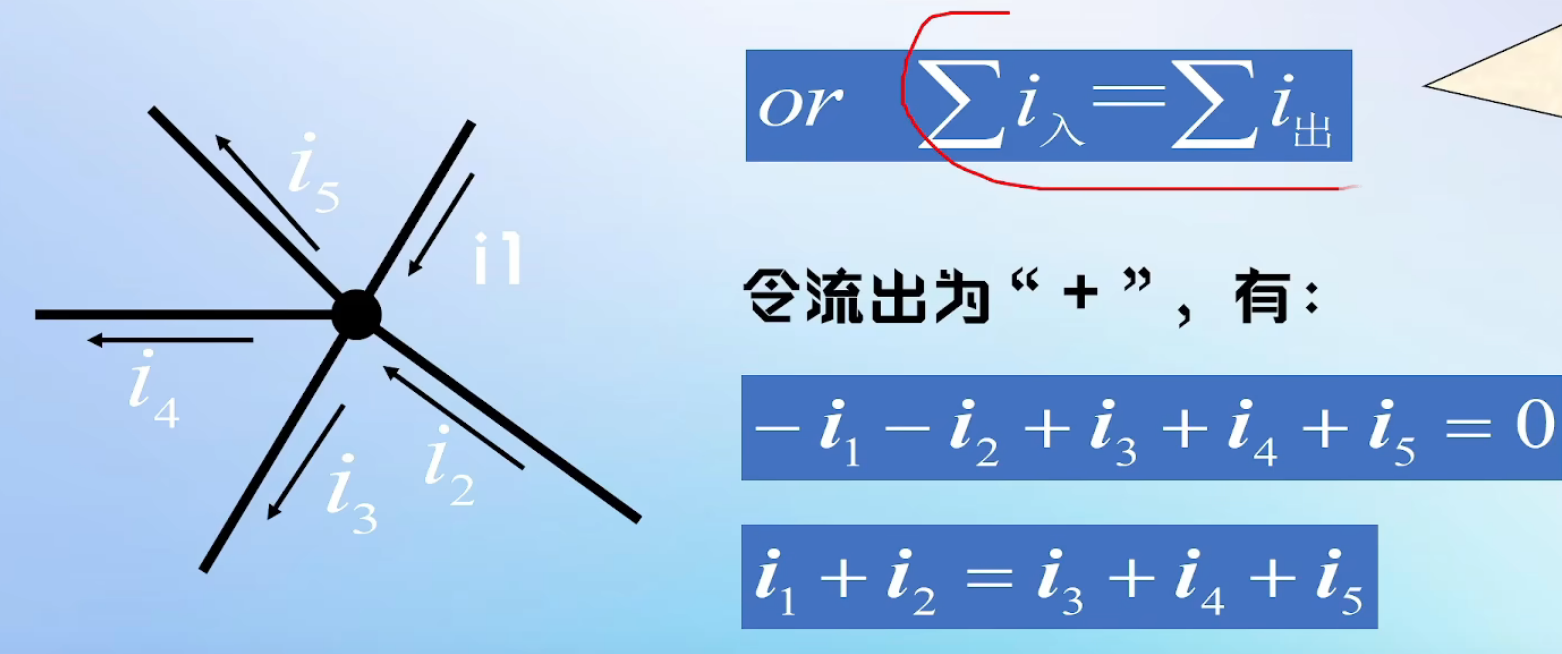
数学表达式:∑i=0(流入节点的电流总和为 0;也可规定 “流出为正”,总和为 0)。
物理类比:就像水管接头 —— 流入多少水,就得流出多少水,否则水会 “凭空消失 / 变多”,这是电荷守恒的体现。
举个例子:一个节点连了 5 条支路,电流分别为i1,i2,−i3,i4,−i5(负号表示 “实际电流方向与假设方向相反”),列方程就是:
i1+i2−i3+i4−i5=0
延伸应用:KCL 还能推广到 “闭合面”—— 比如把几个节点圈起来当一个 “大节点”,流入闭合面的总电流也为 0。
(3)基尔霍夫电压定律(KVL):“能量不能凭空产生”
数学表达式:∑u=0(回路中各元件电压的代数和为 0)。
列写步骤:
- 给每个元件标注 “电压参考方向”(比如假设电流从左流到右,电阻的电压为 “左正右负”);
- 选一个 “回路绕行方向”(顺时针 / 逆时针);
- 绕行时,电势升高的电压记为正,电势降低的记为负,总和为 0。
物理类比:像爬山 —— 从起点出发绕一圈回到起点,海拔高度的变化总和为 0(能量守恒)。
比如一个回路有 4 个元件,电压分别为u1,−u2,u3,−u4(负号表示 “实际电压极性与假设相反”),方程就是:
u1−u2+u3−u4=0
四、定理小结:KCL 和 KVL 的 “配合打法”
- KCL 管 “电流”:约束节点(或闭合面)的电流关系,与元件是电阻、电容还是电感无关;
- KVL 管 “电压”:约束回路的电压关系,也与元件性质无关;
- 适用范围:仅在 “集总参数电路” 中有效;
- 解题逻辑:单独用 KCL 或 KVL 无法完整求解,需联合两者,才能算出电路的电流、电压等参数。
电路分析的基础,就像盖房子的 “地基”—— 原理图元素是 “砖头”,支路、回路是 “骨架”,基尔霍夫定律是 “水泥”。把这些搞扎实,后面分析复杂电路才不会慌

与谐波分析)






)
)
详解)


)





