目录

一、概述

1、逻辑回归

2、激活函数  sigmoid函数

3、最大似然估计

二、逻辑回归

1、原理

2、损失函数

3、代码

三、混淆矩阵

1、定义

2、举例

3、代码

四、分类评估方法

1、精确率（Precision）

2、召回率（Recall）

3、F1（score）

4、代码

五、ROC曲线、AUC指标

1、ROC曲线

2、ROC 曲线图像中，4 个特殊点的含义

3、案例：ROC 曲线的绘制

4、AUC指标：曲线下面积

六、每日回顾

一、概述

1、逻辑回归

        逻辑回归是一种广泛应用于分类任务的统计模型，尤其擅长解决二分类问题（例如预测邮件是否为垃圾邮件、客户是否会购买产品等）。它通过逻辑函数（如Sigmoid函数）将线性回归的输出映射到[0,1]区间，从而得到事件发生的概率。尽管名称中包含"回归"，但它实际上是一种分类算法。        

原理：把线性函数的输出作为激活函数输入，设置阈值完成分类

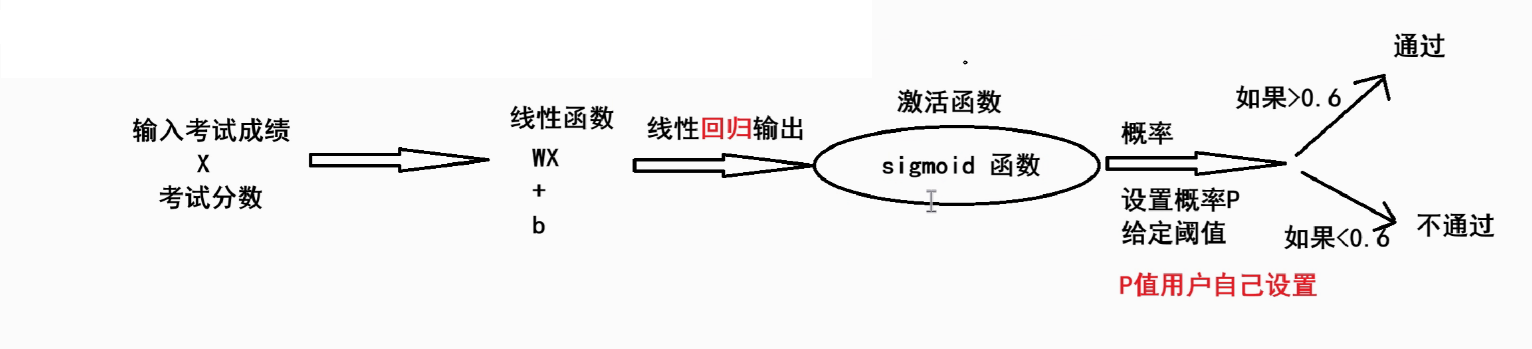
2、激活函数  sigmoid函数

        Sigmoid函数（也叫Logistic函数）是机器学习和神经网络中一个非常经典的非线性函数。它的核心作用是将任意实数输入映射到(0,1)区间，这个特性使其特别适合处理概率和二分类问题。

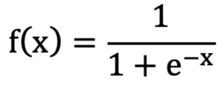
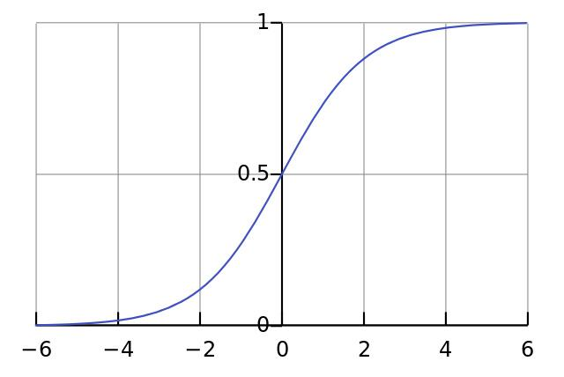
作用：把(-∞, +∞) 映射到 (0， 1)，增加模型的非线性因素

单调递增函数，拐点在x=0，y=0.5（可自定义）的位置

导函数公式：

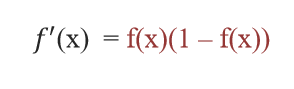
优点​​：

​​        输出概率解释​​：其输出值在(0,1)区间，天然适合解释为概率

        平滑可导​​：函数全程平滑且易于求导，便于在其基础上进行梯度下降等优化算法

缺点​​：

        梯度消失​​：当输入值的绝对值较大时（对应输出接近0或1），其导数会趋近于0。在深层神经网络中，这可能导致梯度在反向传播过程中逐渐变小并消失，使得网络训练困难

        输出非零中心​​：Sigmoid函数的输出恒为正值。这可能导致在训练过程中，权重更新时产生“之”字形抖动，收敛速度变慢

​​        计算成本​​：涉及指数运算（e^{-x}），计算量较大

3、最大似然估计

根据观测到的结果来估计模型算法中的未知参数

最大似然估计的基本原理是​​“既然事件已经发生，就假设它的发生概率是最大的”​​。这是一种在已知结果的前提下，反向推测最可能的原因（参数）的思维方式。

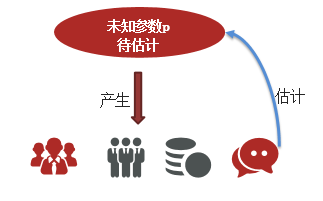
例子：

假设有一枚不均匀的硬币，出现正面的概率和反面的概率是不同的。假定出现正面的概率为𝜃

抛了6次得到如下现象 D = {正面，反面，反面，正面，正面，正面}。每次投掷事件都是相互独立的。则根据产生的现象D，来估计参数𝜃是多少？

f(𝜃) = θ⁴(1−θ)² 令导数=0求极值，可估计出𝜃值

二、逻辑回归

1、原理

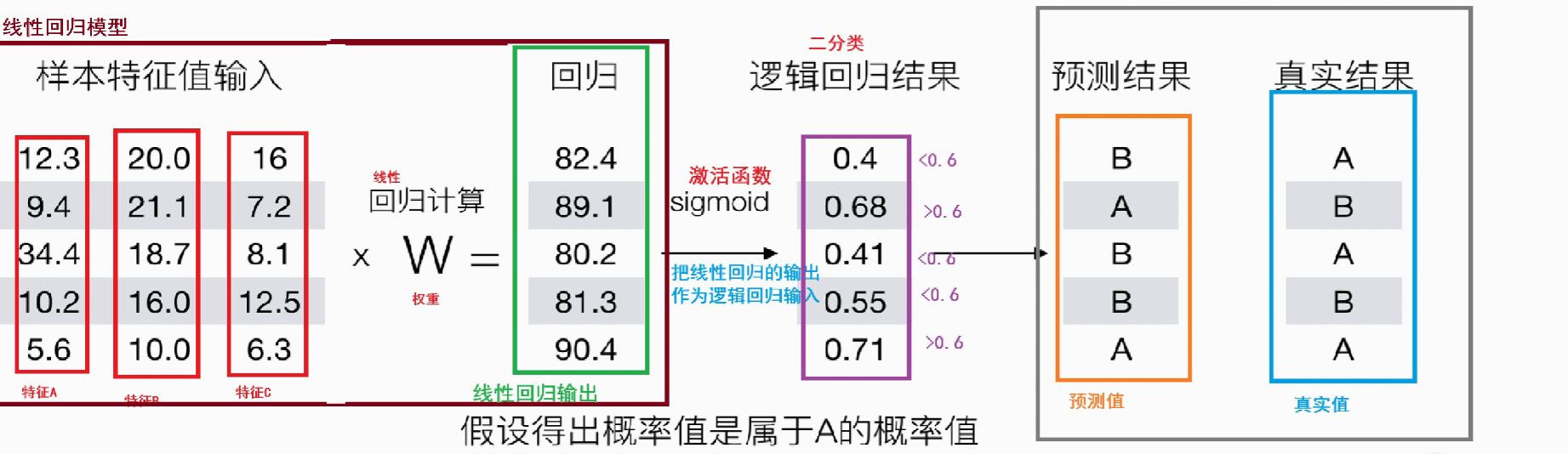
​​        利用一个线性回归模型的计算结果，再通过一个Sigmoid激活函数，将这个结果映射到0到1之间，将其解释为“属于某个类的概率”​​。

把线性回归的输出，作为逻辑回归的输入

2、损失函数

损失函数的工作原理：每个样本预测值有A、B两个类别，真实类别对应的位置，概率值越大越好

3、代码

import pandas as pd
import numpy as np
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScalerdata = pd.read_csv("breast-cancer-wisconsin.csv")
print('清洗前数据集大小为：',data.shape)
# 数据清洗处理
# 将数据中的问号("?")替换为NaN值，然后删除包含NaN值的行
# 这样可以清理掉无效或缺失的数据记录
data = data.replace(to_replace="?", value=np.nan)
data = data.dropna()
print('清洗后数据集大小为：', data.shape)# x = data[data.columns[1:-1]]
x = data.iloc[:, 1:-1]
y = data['Class']
X_train, X_test, y_train, y_test = (train_test_split(x, y, test_size=0.2, random_state=22))transfor = StandardScaler()
X_train = transfor.fit_transform(X_train)
X_test = transfor.transform(X_test)es = LogisticRegression()
es.fit(X_train, y_train)y_predict = es.predict(X_test)
print('预测结果：\n', y_predict)
acc = accuracy_score(y_test, es.predict(X_test))
print('准确率：', acc)

三、混淆矩阵

1、定义

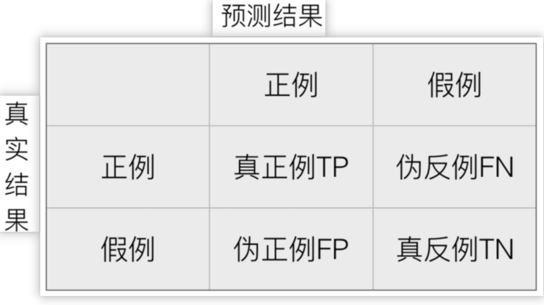
真实值是 正例 的样本中，被分类为 正例 的样本数量有多少，叫做真正例（TP，True Positive）
真实值是 正例 的样本中，被分类为 假例 的样本数量有多少，叫做伪反例（FN，False Negative）
真实值是 假例 的样本中，被分类为 正例 的样本数量有多少，叫做伪正例（FP，False Positive）
真实值是 假例 的样本中，被分类为 假例 的样本数量有多少，叫做真反例（TN，True Negative）

2、举例

已知：样本集10样本，有 6 个恶性肿瘤样本，4 个良性肿瘤样本，我们假设恶性肿瘤为正
模型A：预测对了 3 个恶性肿瘤样本，4 个良性肿瘤样本，计算：TP、FN、FP、TN

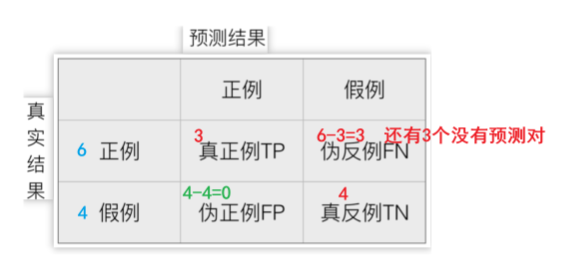
真正例 TP 为：3         伪反例 FN 为：3

伪正例 FP 为：0        真反例 TN 为：4

3、代码

from sklearn.metrics import confusion_matrix
import pandas as pd# 已知：样本集10个样本，有 6个恶性肿瘤样本，4个良性肿瘤样本，我们假设恶性肿瘤为正
# 1、定义真实数据值，手动设置正反例
y_train = ['恶性', '恶性', '恶性', '恶性', '恶性', '恶性','良性', '良性', '良性', '良性']label = ['恶性', '良性']  # 样本标签,标签1为正例，标签2为反例
df_label = ['恶性(正例)', '良性(假例)']# 2、定义预测数据集，手动设置正反例
y_pred_A = ['恶性', '恶性', '恶性','良性', '良性', '良性', '良性', '良性', '良性', '良性']# 3、计算混淆矩阵
# 参数1：真实值，参数2：预测值，参数3：标签
cm_A = confusion_matrix(y_train, y_pred_A, labels=label)
print(f"混淆矩阵为：\n{cm_A}")# 4、将混淆矩阵转为DataFrame
# 参数1：矩阵，参数2：行标签，参数3：列标签
df_cm_A = pd.DataFrame(cm_A, index=df_label, columns=df_label)
print(f"混淆矩阵为：\n{df_cm_A}")y_pred_b = ['恶性', '恶性', '恶性','恶性', '恶性', '恶性','恶性', '恶性', '恶性','良性']
cm_b = confusion_matrix(y_train, y_pred_b, labels=label)
df_cm_b = pd.DataFrame(cm_b, index=df_label, columns=df_label)
print(f"混淆矩阵为：\n{df_cm_b}")

运行结果

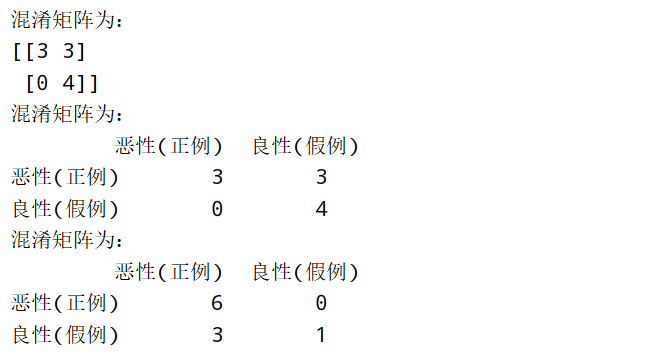
四、分类评估方法

1、精确率（Precision）

查准率，对预测的正例样本准确率。比如：把恶性肿瘤当做正例样本，想知道模型对恶性肿瘤的预测准确率。

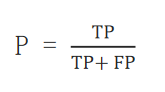
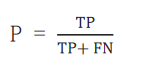
2、召回率（Recall）

也叫查全率，指的是预测为真正例样本占所有真实正例样本的比重。

3、F1（score）

若对模型的精度、召回率都有要求，希望知道模型在这两个评估方向的综合预测能力

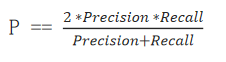
4、代码

from sklearn.metrics import recall_score, f1_score
from sklearn.metrics import precision_score
y_train = ['恶性', '恶性', '恶性', '恶性', '恶性', '恶性','良性', '良性', '良性', '良性']
y_pred_A = ['恶性', '恶性', '恶性','良性', '良性', '良性', '良性', '良性', '良性', '良性']
y_pred_b = ['恶性', '恶性', '恶性','恶性', '恶性', '恶性','恶性', '恶性', '恶性','良性']
def dm01_precision():result1 = precision_score(y_train, y_pred_A, pos_label='恶性')print('模型A的精确率：', result1)result2 = precision_score(y_train, y_pred_b, pos_label='恶性')print('模型B的精确率：', result2)
def dm02_Recall():result1 = recall_score(y_train, y_pred_A, pos_label='恶性')print('模型A的召回率：', result1)result2 = recall_score(y_train, y_pred_b, pos_label='恶性')print('模型B的召回率：', result2)
def dm03_F1():result1 = f1_score(y_train, y_pred_A, pos_label='恶性')print('模型A的F1：', result1)result2 = f1_score(y_train, y_pred_b, pos_label='恶性')print('模型B的F1：', result2)
if __name__ == '__main__':dm01_precision()dm02_Recall()dm03_F1()

五、ROC曲线、AUC指标

1、ROC曲线

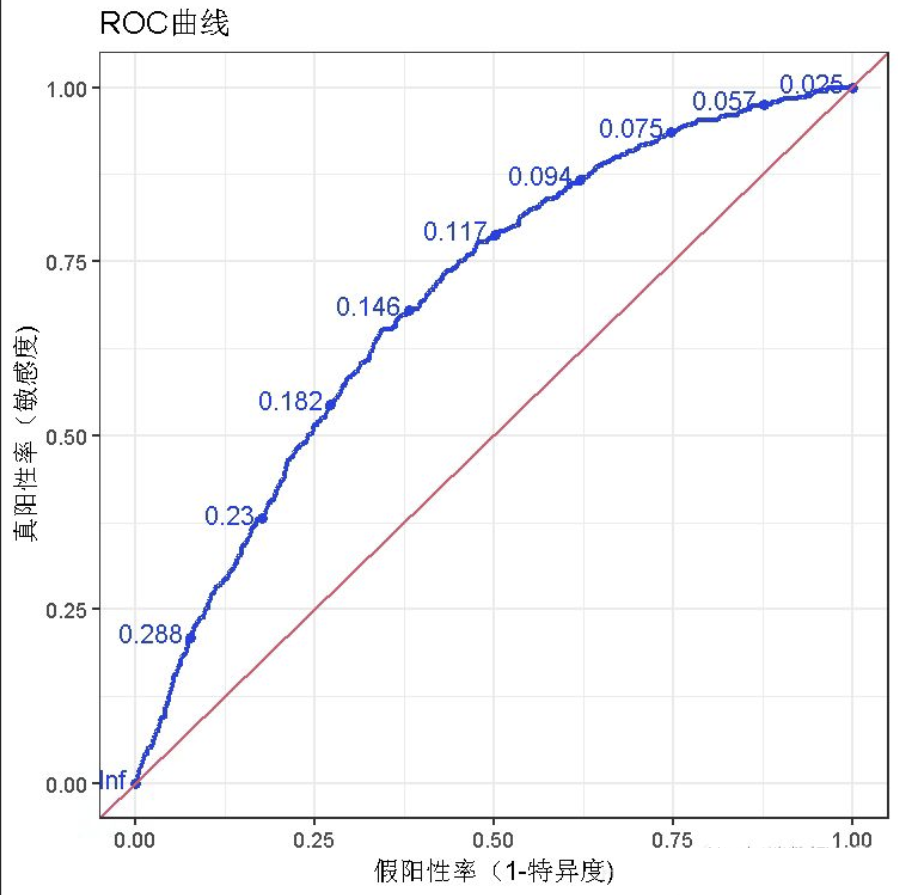
​​ROC曲线​​（Receiver Operating Characteristic Curve，受试者工作特征曲线）是一种图形化工具，用于展示二分类模型在不同分类阈值下的性能表现。它的​​横轴是假阳性率（FPR, False Positive Rate）​​，​​纵轴是真阳性率（TPR, True Positive Rate）​​。

​​真阳性率 (TPR)​​，也称为​​召回率（Recall）​​或​​灵敏度（Sensitivity）​​，计算公式为：TPR = TP / (TP + FN)。它表示​​实际为正例的样本中，被模型正确预测为正例的比例​​。

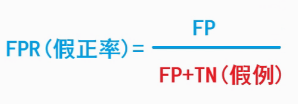
​​假阳性率 (FPR)​​，计算公式为：FPR = FP / (FP + TN)。它表示​​实际为负例的样本中，被模型错误预测为正例的比例。

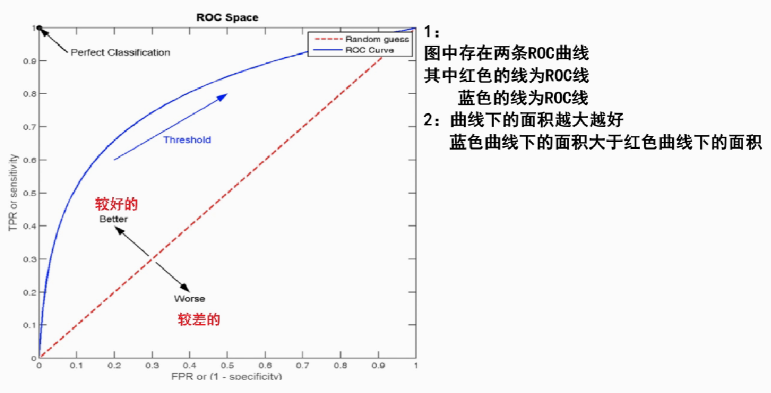
2、ROC 曲线图像中，4 个特殊点的含义

3、案例：ROC 曲线的绘制

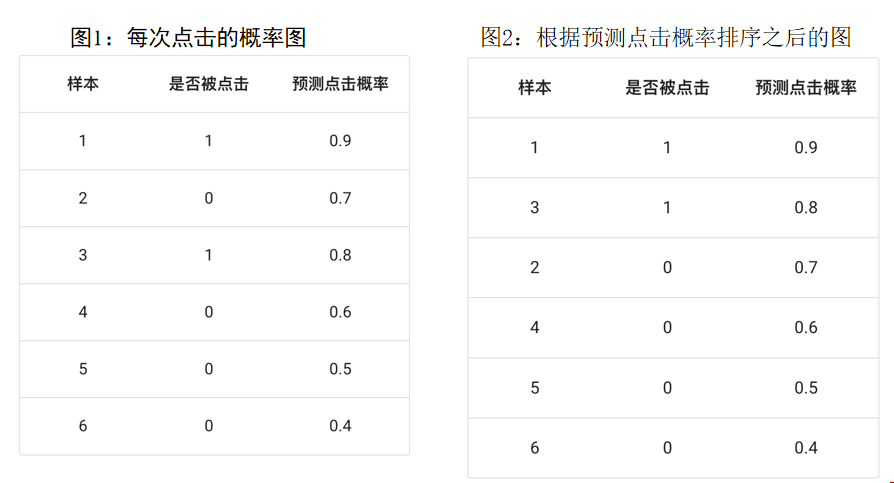
会得出不同阈值下的点坐标：(0, 0)、(0, 0.5)、(0, 1)、(0.25, 1)、(0.5, 1)、(0.75, 1)

则由 TPR 和 FPR 构成的 ROC 图像为

4、AUC指标：曲线下面积

​​AUC​​（Area Under the Curve）则是​​ROC曲线下的面积​​，用于量化模型的整体分类性能。AUC的取值范围在0到1之间。

ROC曲线的优劣可以通过曲线下的面积（AUC）来衡量，AUC越大表示分类器性能越好。​​AUC与ROC曲线​​：AUC就是这条ROC曲线下方的面积。ROC曲线越靠近左上角（即FPR越小，TPR越大），模型的性能通常越好，其AUC值也更接近1。

        当AUC=0.5时，表示分类器的性能等同于随机猜测当
        当AUC=1时，表示分类器的性能完美，能够完全正确地将正负例分类。
      （AUC=0时也可以，完美相反地正确预测）

AUC的核心优势在于其​​对类别不平衡不敏感​​，且​​综合了模型在所有可能阈值下的表现​​。理解其​​概率解释​​（随机正样本得分高于随机负样本的概率）有助于更深刻地把握其内涵。

六、每日回顾

1：逻辑回归主要解决什么类型的问题？逻辑回归的流程是什么 ？

2：混淆矩阵的四个基本元素（TP、TN、FP、FN）分别代表什么含义？

3：精确率（Precision）、召回率（Recall）的计算公式是什么？分别反映模型的什么能力？

4：ROC 曲线的横纵轴分别是什么？曲线上的每个点代表什么含义？

5：AUC 指标的含义是什么？其取值范围是多少？AUC=0.5、AUC=1 、AUC=0分别说明模型的什么性能？