信号调制与解调 matlab仿真
- 原始信号--频谱为cos(Wt*w)函数,外形如馒头
- 调制
- 解调
- 傅里叶变换
- 测试FT的频谱是否为锯齿波
- 理想低通滤波器,截至频率Wm
- 傅里叶变换
- 频谱为锯齿波函数的时域信号函数
- 傅里叶变换
- 调制频率1
- 理想低通滤波
- 调制频率2
- 理想低通滤波
% 调制定理演示Demo % 频域三角信号×G(w)门函数,得到锯齿波频谱 %解 [MATLAB程序]
T = 20; %采样周期 dt = 0.02; %积分时间, 采样时间 t = -T/2:dt:T/2;
原始信号--频谱为cos(Wt*w)函数,外形如馒头
Wm = 5; % 截至角频率--与横坐标交点 Wt = pi/(2*Wm); % cos(Wt*w) ft = Wm*sinc(Wm*(t+Wt)/pi) + Wm*sinc(Wm*(t-Wt)/pi); ft = ft / (2*pi); % 乘以系数Wc = 15; % 调制信号角频率Wc
调制
ft1 = ft .* cos(Wc*t); % 使用cos(Wc*t)调制ft
解调
ft2 = ft1 .* cos(Wc*t); % 使用cos(Wc*t)解调ft
傅里叶变换
W1 = 50;
N = 500;
k = -N:N;
W = k*W1/N;
% f(t)傅里叶变换
F0 = ft*exp(-j*t'*W)*dt; %求F(t)的傅里叶变换F1(jw)
F0 = abs(F0);
F1 = ft1*exp(-j*t'*W)*dt; %求F(t)*cos(Wc*t)的傅里叶变换F1(jw)
F1 = abs(F1);
F2 = ft2*exp(-j*t'*W)*dt; %求f1(t)*cos(Wc*t)*cos(Wc*t)的傅里叶变换F1(jw)
F2 = abs(F2);%%显示波形
subplot(3,1,1)
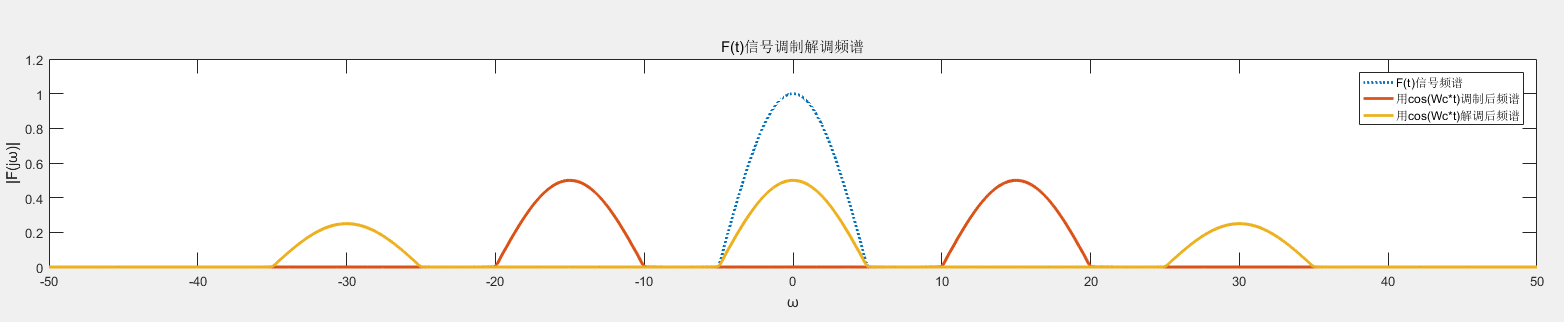
plot(W, F0, ':', W, F1, W, F2, 'linewidth', 2)
legend('F(t)信号频谱', '用cos(Wc*t)调制后频谱', '用cos(Wc*t)解调后频谱');
xlabel('ω')
ylabel('|F(jω)|')
title('F(t)信号调制解调频谱')
测试FT的频谱是否为锯齿波
T = 20; % 采样周期 Fs = 100; % 采样频率 dt = 1/Fs; % 积分时间, 采样时间 t = -T/2:dt:T/2;
理想低通滤波器,截至频率Wm
Wm = 2*pi*9; % 理想低通滤波器的截至频率 filter = Wm/pi*sinc(Wm*t/pi); % Wc/π*Sa(Wc*t) 理想低通滤波函数
傅里叶变换
W1 = 2*pi*100; N = 500; k = -N:N; W = k*W1/N;
频谱为锯齿波函数的时域信号函数
Wc = 2*pi*5; % 基本频率 W0 = 2*pi*30; % 频移--移出2个信号ft = Wc/pi.*(sinc(Wc*t/pi).^2); % 频谱为三角信号的函数 fr1 = Wc/pi.*sinc(Wc*t/pi).*exp(-j*Wc*t); % 频谱为G(w)门函数(移频) ft1 = conv2(ft, fr1, 'same')*dt; % 频域三角信号×G(w)门函数,得到锯齿波频谱 ft1 = ft1.*exp(j*W0*t);fr2 = Wc/pi.*sinc(Wc*t/pi).*exp(j*Wc*t); % 频谱为G(w)门函数(移频) ft2 = conv2(ft, fr2, 'same')*dt; % 频域三角信号×G(w)门函数,得到锯齿波频谱 ft2 = ft2.*exp(-j*W0*t); ft = ft1 + ft2;
傅里叶变换
F3 = ft*exp(-j*t'*W)*dt; %求f1(t)的傅里叶变换F1(jw) F3 = abs(F3);
调制频率1
Fy = 22; % 调制频率 ft1 = ft.*cos(2*pi*Fy*t); % 调制信号
理想低通滤波
ft1 = conv2(ft1, filter, 'same')*dt; % 理想低通滤波
F4 = ft1*exp(-j*t'*W)*dt; %求f1(t)的傅里叶变换F1(jw)
F4 = abs(F4);subplot(3,1,2)
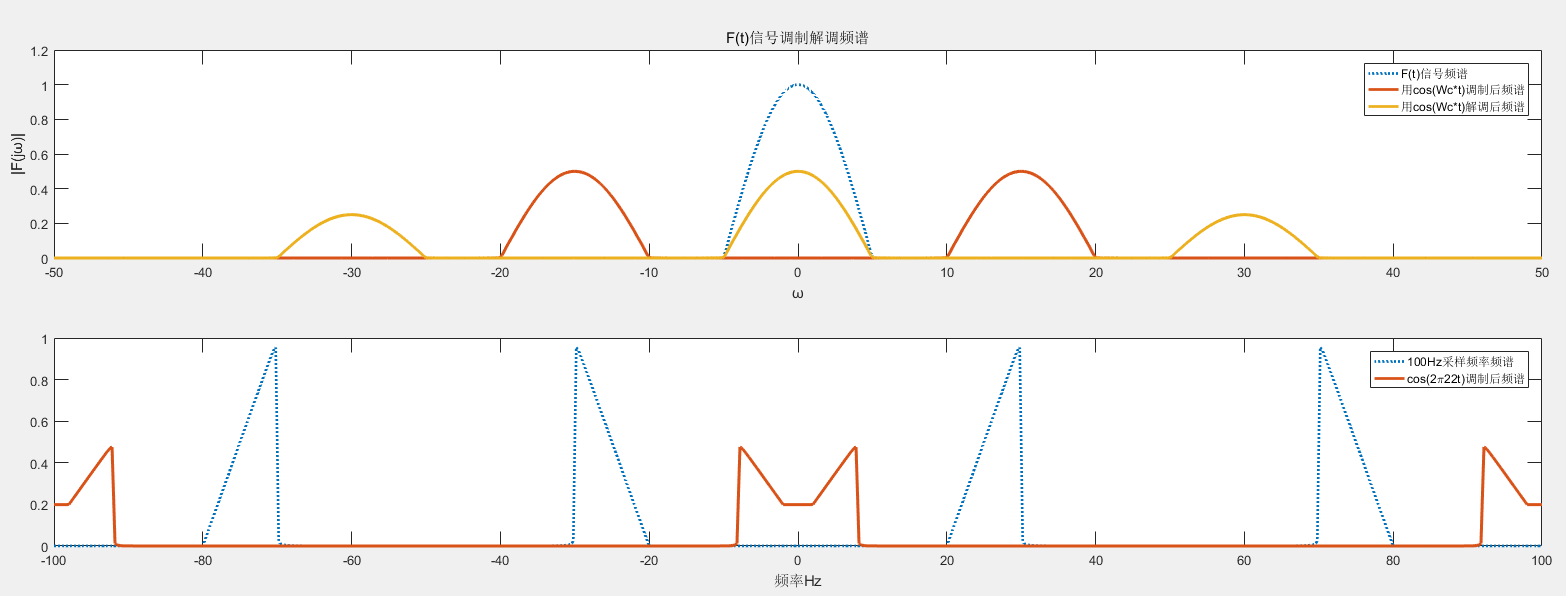
plot(W/(2*pi), F3, ':', W/(2*pi), F4, 'linewidth', 2);
legend('100Hz采样频率频谱', 'cos(2\pi22t)调制后频谱');
xlabel('频率Hz')
调制频率2
Fy = 25; % 调制频率 ft2 = ft.*cos(2*pi*Fy*t); % 调制信号
理想低通滤波
ft2 = conv2(ft2, filter, 'same')*dt; % 理想低通滤波
F4 = ft2*exp(-j*t'*W)*dt; %求f1(t)的傅里叶变换F1(jw)
F4 = abs(F4);subplot(3,1,3)
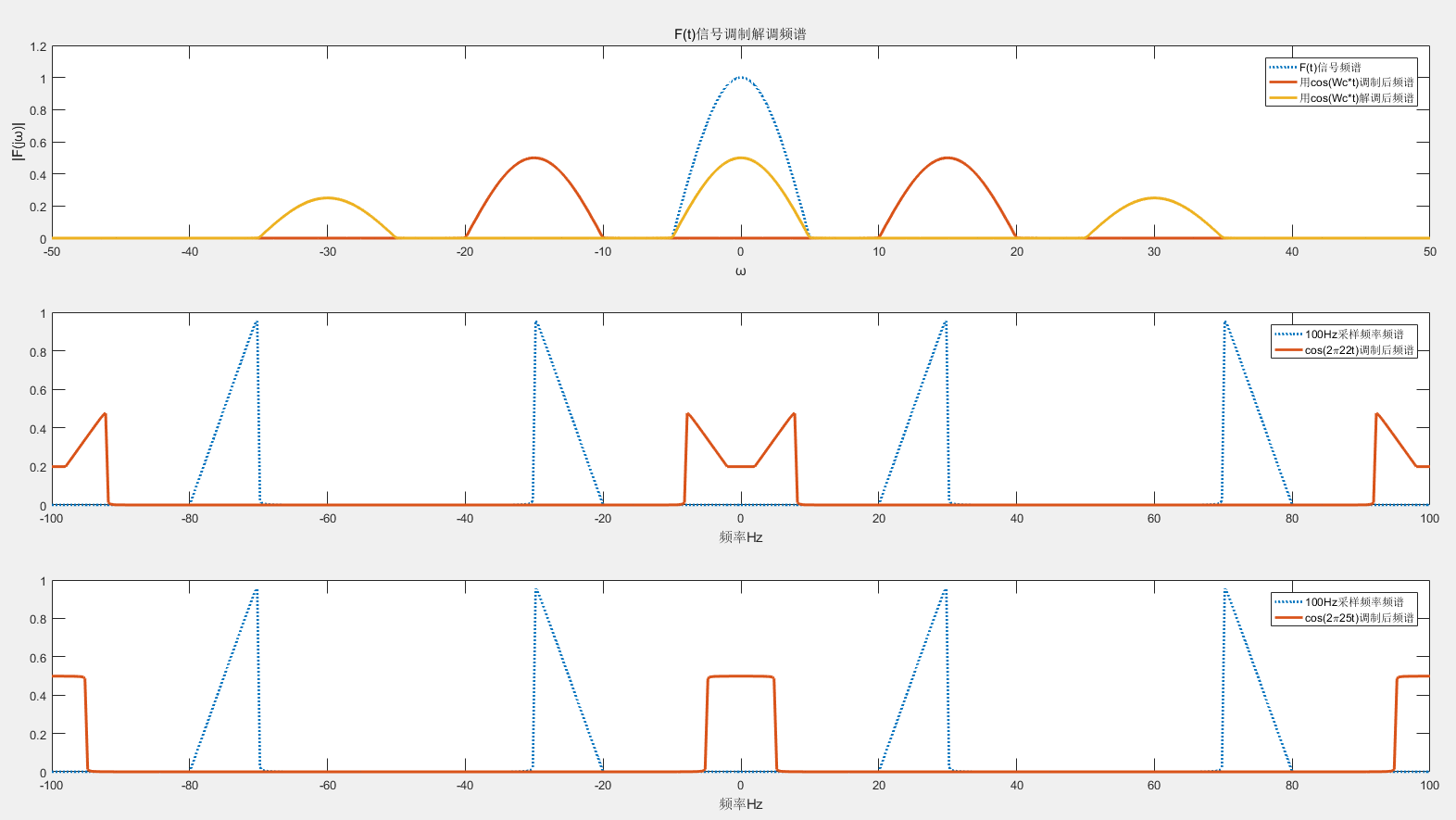
plot(W/(2*pi), F3, ':', W/(2*pi), F4, 'linewidth', 2);
legend('100Hz采样频率频谱', 'cos(2\pi25t)调制后频谱');
xlabel('频率Hz')
还可以直接利用采样频移,
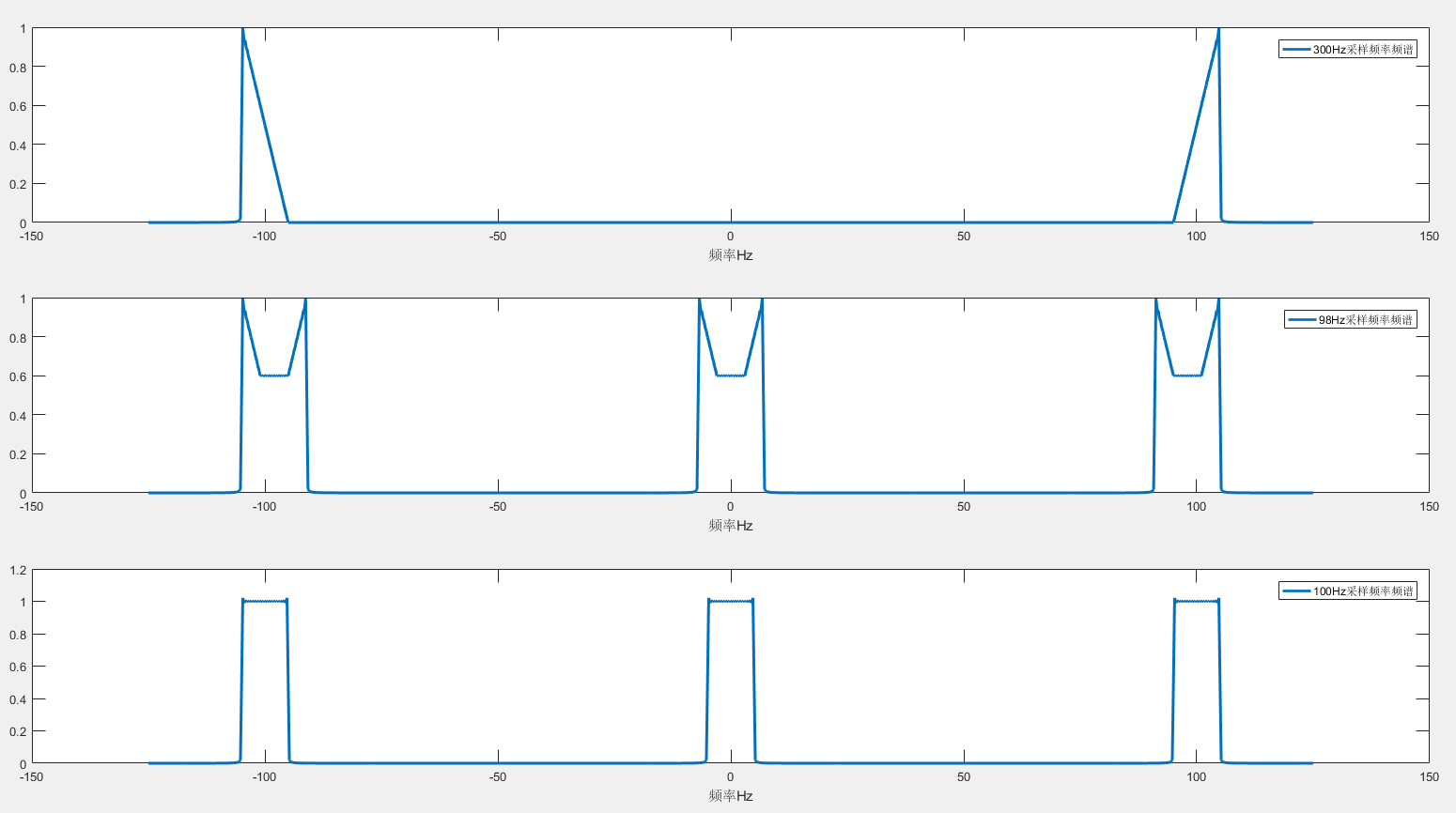
使用采样频移可参见不同采样率的频谱-CSDN博客



)



)




)

)


)


)