MATLAB 代码实现了一个基于物理信息神经网络（Physics-Informed Neural Network, PINN）的三维波动方程求解器。以下是详细分析：
🧠 一、主要功能
🔗 二、逻辑关联
代码结构清晰，分为五个主要部分：
- 问题定义与数据生成：定义方程参数、初始/边界条件，生成训练点。
- 神经网络构建：构建一个全连接网络，输入为
(x, y, z, t)，输出为u。 - 损失函数定义：包含 PDE 残差、初始条件、边界条件三部分。
- 训练循环：使用 Adam 优化器训练网络。
- 可视化：绘制损失曲线、波场切片和生成传播动画。
📐 三、算法步骤
-
数据采样：
- 内部点：随机采样
(x, y, z, t) - 初始条件点：
t=0处采样(x, y, z) - 边界条件点：在六个边界面上采样
(x, y, z, t)
- 内部点：随机采样
-
网络前向传播：
- 输入：
[x, y, z, t]（转换为dlarray格式，支持自动微分） - 输出：
u(x, y, z, t)
- 输入：
-
损失计算：
- PDE 残差损失：使用自动微分计算二阶导数，构造波动方程残差。
- 初始条件损失：确保
u(x,y,z,0)和u_t(x,y,z,0)满足初始条件。 - 边界条件损失：确保边界上
u=0。
-
反向传播与优化：
- 使用
dlgradient计算梯度，adamupdate更新参数。
- 使用
-
可视化：
- 绘制损失曲线（对数坐标）
- 绘制
z=0平面在不同时间的波场分布 - 生成波场传播动画
🧪 四、技术路线
- PINN 框架：将物理方程嵌入损失函数，引导网络学习物理规律。
- 自动微分（AD）：使用
dlgradient计算高阶导数，避免数值差分误差。 - 深度学习工具箱：使用
dlnetwork构建网络，支持自定义训练循环。 - 多任务损失：联合优化 PDE 残差、初始条件和边界条件。
📘 五、公式原理
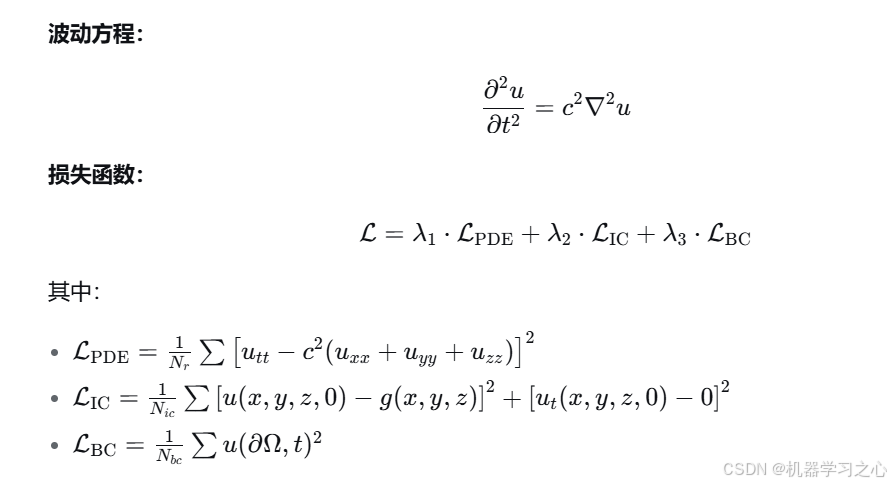
⚙️ 六、参数设定
| 参数 | 值 | 说明 |
|---|---|---|
c | 1.0 | 波速 |
x_min, x_max | -1, 1 | x 范围 |
y_min, y_max | -1, 1 | y 范围 |
z_min, z_max | -1, 1 | z 范围 |
t_min, t_max | 0, 1 | 时间范围 |
N_r | 5000 | 内部残差点数 |
N_ic | 1000 | 初始条件点数 |
N_bc | 1000 | 边界条件点数 |
numLayers | 5 | 隐藏层数 |
numNeurons | 100 | 每层神经元数 |
numEpochs | 1000 | 训练轮数 |
learningRate | 1e-3 | 学习率 |
💻 七、运行环境
- 软件：MATLAB（推荐 R2024a 或更高版本）
✅ 总结
该代码实现了一个完整的 PINN 求解三维波动方程的流程，结合了深度学习与物理建模，适用于无解析解或复杂边界条件下的波动问题。通过自动微分计算高阶导数，避免了传统数值方法的离散误差，具有较强的通用性和可扩展性。
” 报错)
