题面链接：Dashboard - Codeforces Round 1028 (Div. 2) - Codeforces

A. Gellyfish and Tricolor Pansy

思路

要知道骑士如果没了那么这个人就失去了攻击手段，贪心的来说我们只需要攻击血量少的即可，那么取min比较一下即可

代码

void solve(){int a,b,c,d;cin>>a>>b>>c>>d;int x=min(a,c);int y=min(b,d);if(x>=y){cout<<"Gellyfish\n";}else{cout<<"Flower\n";}
}

B. Gellyfish and Baby's Breath

思路

根据给的公式对于每个要求最大值，我们对于i来说其结果为   注意到p和q出现的都是0-i

因此对于每个只需要维护一下和的最大值然后取最大即可，可以用前缀和来维护

特别注意这里对于2的次方预处理更好一些

代码

#include<bits/stdc++.h>
using namespace std;#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL); 
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;const int N=2e5+10;
const int inf=1e18;
const int mod=998244353;int qpow(int a,int b){int ans=1;while(b){if(b&1){ans=(ans*a)%mod;}a=((a%mod)*(a%mod))%mod;b>>=1;}return ans;
}void solve(){int n;cin>>n;vi p(n);vi q(n);for(int i=0;i<n;i++){cin>>p[i];}vector<int> pp(n+10);int mx=p[0];pp[0]=0;for(int i=1;i<n;i++){pp[i]=pp[i-1];if(p[i]>mx){mx=p[i];pp[i]=i;}}for(int i=0;i<n;i++){cin>>q[i];}vector<int> pq(n+10);mx=q[0];pq[0]=0;for(int i=1;i<n;i++){pq[i]=pq[i-1];if(q[i]>mx){mx=q[i];pq[i]=i;}}vi r(n+10);for(int i=0;i<n;i++){if(p[pp[i]]>q[pq[i]]){r[i]=(qpow(2,p[pp[i]])+qpow(2,q[i-pp[i]]))%mod;}else if(p[pp[i]]<q[pq[i]]){r[i]=(qpow(2,p[i-pq[i]])+qpow(2,q[pq[i]]))%mod;}else{if(q[i-pp[i]]>p[i-pq[i]]){r[i]=(qpow(2,p[pp[i]])+qpow(2,q[i-pp[i]]))%mod;}else{r[i]=(qpow(2,p[i-pq[i]])+qpow(2,q[pq[i]]))%mod;}}}for(int i=0;i<n;i++){cout<<r[i]<<" ";}cout<<"\n";
}
signed main() {vcoistntcout<<fixed<<setprecision(2);int _=1;cin>>_;while(_--) solve();return 0;
}

C. Gellyfish and Flaming Peony

思路

贪心的来看我们最后要求的序列一定是全变成数列的gcd的

对于数列中存在gcd的数列我们可以直接用此gcd来改变其他数列的值

否则我们需要求出数列中最小的子集让子集的gcd=全局的gcd

对于第二部分我们可以 先将数组/gcd处理后 求所有数的gcd=1的最小子集的长度

我们用dp[i]表示gcd为i的时候的最小子集长度，需要dp[1]

代码

#include<bits/stdc++.h>
using namespace std;#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL); 
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;const int inf = 1e18;void solve() {int n;cin>>n;vi a(n);int g=0;for (int i=0;i<n;i++){cin>>a[i];g=__gcd(g,a[i]);}int ct=0;for (int i=0;i<n;i++) {if (a[i]==g) ct++;}if (ct>0){cout<<n-ct<<"\n";return;}vi b;for (int i = 0; i < n; i++) {b.push_back(a[i] / g);}vector<int> dp(5001, inf);dp[0]=0;for (int x:b) {vector<int> tdp = dp;for (int d=0;d<=5000;d++) {if (dp[d]==inf) continue;int tg=__gcd(d,x);if (tg<=5000){if (tdp[tg]>dp[d]+1){tdp[tg]=dp[d]+1;}}}dp=tdp;}int s=dp[1];cout<<s+n-2<<"\n";
}
signed main() {vcoistntcout<<fixed<<setprecision(2);int _=1;cin>>_;while(_--) solve();return 0;
}

D. Gellyfish and Camellia Japonica

思路

感觉是个很有意思的题，首先我们在进行构思的时候要对操作倒着来以达到还原原数组的目的

对于所有的操作我们可以试着构造一个二叉树的森林以z为父节点x,y为孩子节点

以样例2，3为例其构造出来的二叉树如下

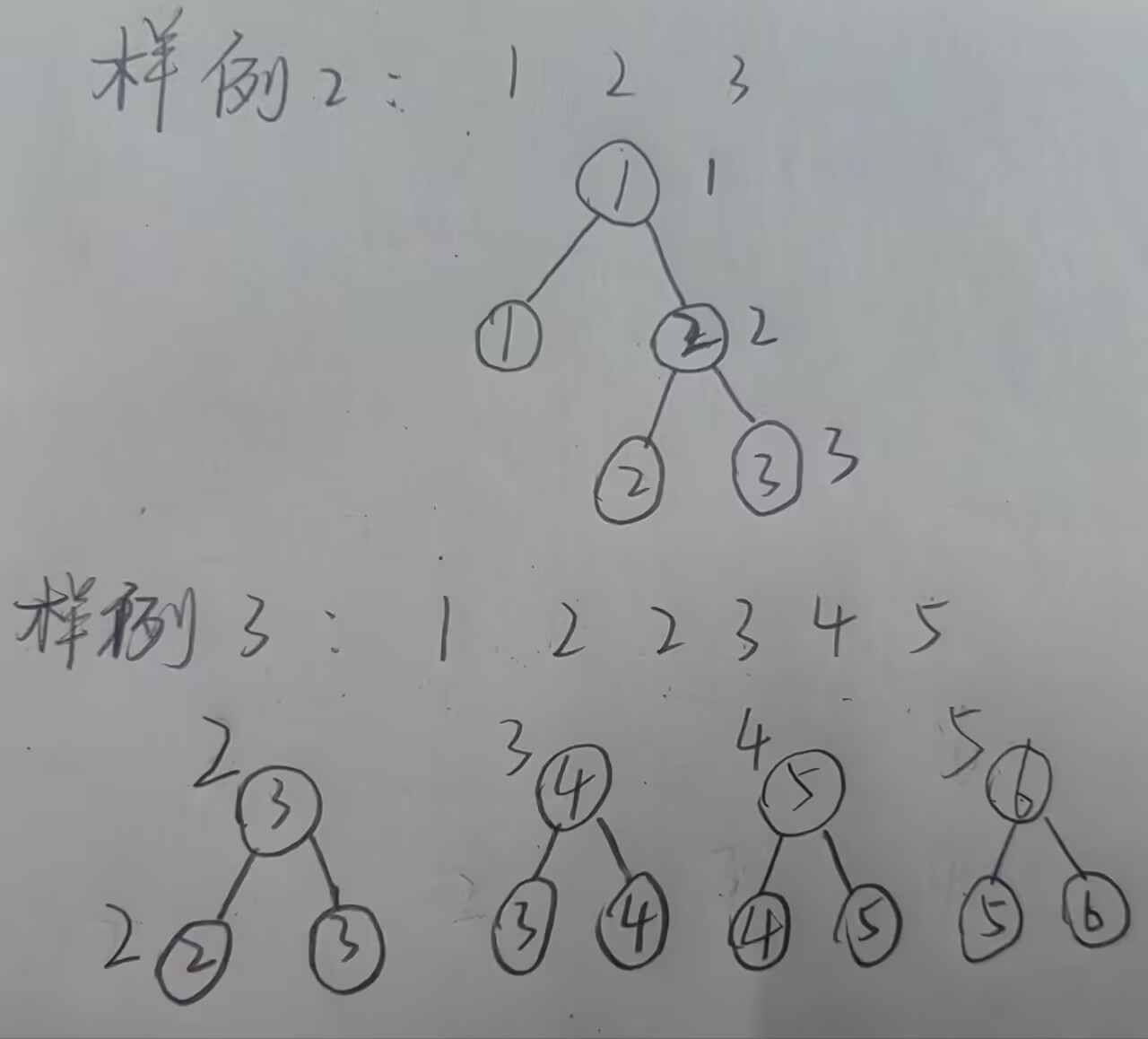
不难发现从左到右从根节点出发遇到的第一个出现的节点的值就是已经处理完之后a[i]的值，并且很容易观察出我们要求叶子节点的值

得到此结论后可以根据此树的建树过程来表示出孩子节点的上界a[x]=max(a[x],a[z])以及a[y]=max(a[y],a[z])

以此来统计出每个节点的上界，再模拟下过程看得到的数组是否和原数组相同，不相同则输出-1

代码

#include<bits/stdc++.h>
using namespace std;#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL); 
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;const int N=2e5+10;
const int inf=1e18;
const int mod=998244353;void solve(){int n,q;cin>>n>>q;vi a(n+1);for(int i=1;i<=n;i++){cin>>a[i];}vi c=a;vector<array<int,3>> Q(q+1);for(int i=1;i<=q;i++){cin>>Q[i][0]>>Q[i][1]>>Q[i][2];}for(int i=q;i>=1;i--){auto [x,y,z]=Q[i];a[x]=max(a[x],a[z]);a[y]=max(a[y],a[z]);if(z!=x&&z!=y){     //特别注意此特判a[z]=0;}}vi b=a;for(int i=1;i<=q;i++){auto [x,y,z]=Q[i];b[z]=min(b[x],b[y]);}if(b!=c){cout<<"-1\n";return;}for(int i=1;i<=n;i++){cout<<a[i]<<" \n"[i==n];}}
signed main() {vcoistntcout<<fixed<<setprecision(2);int _=1;cin>>_;while(_--) solve();return 0;
}