排序的概念
排序：就是将一串东西，按照要求进行排序，按照递增或递减排序起来

稳定性：就是比如排序中有两个相同的数，如果排序后，这两个相同的数相对位置不变，这说明是稳定的，反之不稳定

插⼊排序

思想：就是将一个后面未排序的数，从后向前面有序的数进行扫描，找到对应为止插入，就像平时玩扑克牌一样

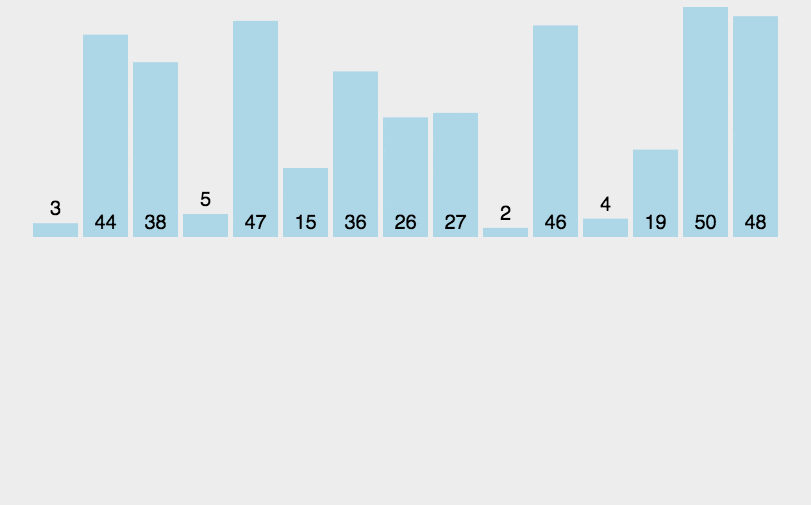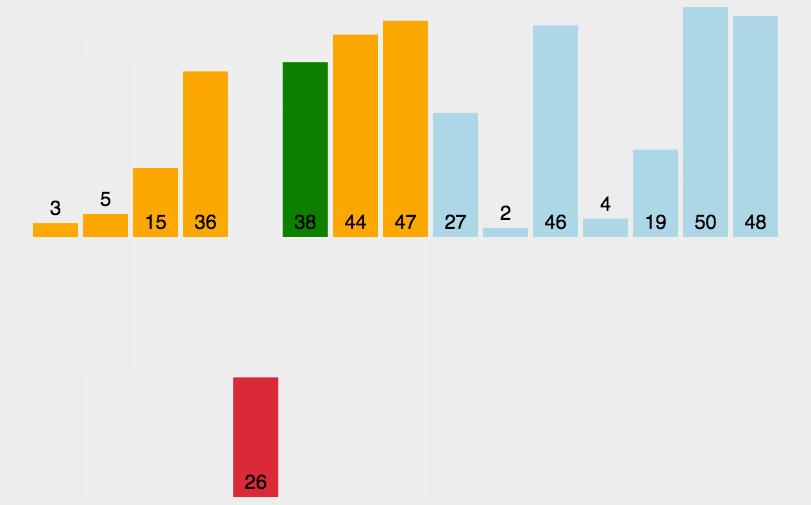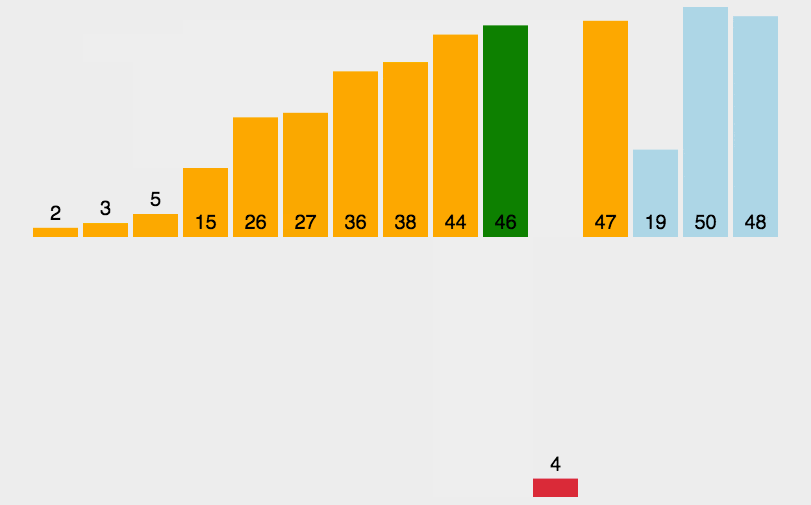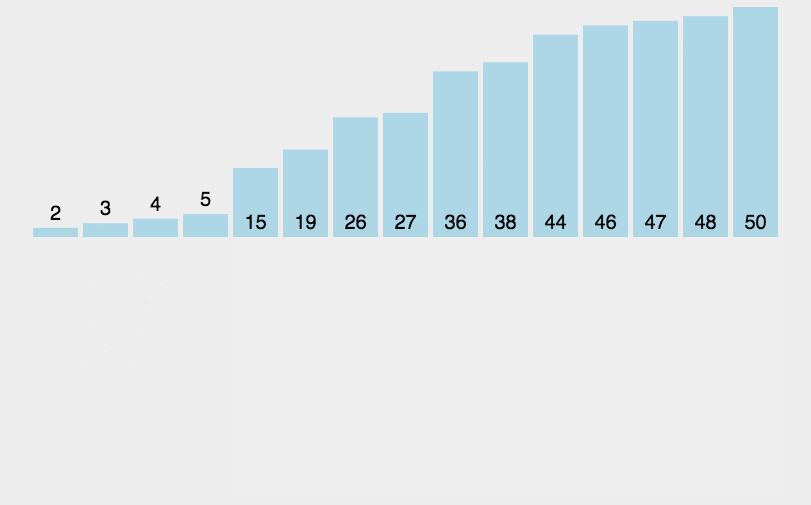
1.遍历整个数组，定义一个临时遍历tem存储当前要排序的值的值
2.当前元素与其前面元素进行比较
如果当前值大于tem就将这个值向后移动，反之就找到了退出，将该下标后面的值赋值为tem，array[ j + 1] = tem

public class Test {public static void main(String[] args) {int[] array = {3,1,2,3,4};insertSort(array);System.out.println(Arrays.toString(array));}//快速排序public static void insertSort(int[] array){for (int i = 1; i < array.length; i++) {int tem = array[i];int j = i-1;for (; j >=0 ; j--) {//如果存在下标j的值大于tem//就将这个值向后移动if(array[j]>tem){array[j+1] = array[j];}else {break;}}//最后将找到的j的后面那个值赋值给temarray[j+1] = tem;}}
}

运行结果如下

时间复杂度：O(N^2) ，因为这里最慢是1+2+3……+n,求和 n(n+1) / 2
空间复杂度：O(1)，这里就多开辟了tem
稳定性：稳定，这里再遇到<=tem就会退出循环，所以说遇到相同的并不会改变位置
并且可以发现如果元素集合越接近有序，其方式更高效

希尔排序

希尔排序（Shell Sort）是插入排序的一种改进版本
思想：它通过将待排序的列表分成若干子列表，对每个子列表进行插入排序，逐步缩小子列表的间隔，最终完成整个序列的排序

1.先选择增量序列：选择gap，用于将其分为若干子序列，经常就是采用（n / 2 ,n/4……1）
2 .分组进行插入排序，逐渐的缩小增量，直到增量为1，在对整个序列进行一次插入排序，就完成排序了

public class Test {public static void main(String[] args) {int[] array = {3,1,2,3,4};shellSort(array);System.out.println(Arrays.toString(array));}public static void shellSort(int[] array){int gap = array.length;//先进行分组进行插入排序while(gap>1){gap = gap/2;//确定分几组shell(array,gap);}}public  static void shell(int[] array,int gap){for (int i = gap; i < array.length; i++) {//根据组进行排序int tem = array[i];int j = i-gap;for (; j >=0 ; j-=gap) {//如果存在下标j的值大于tem//就将这个值向后移动if(array[j]>tem){array[j+gap] = array[j];}else {break;}}array[j+gap] = tem;}}
}

运行结果如下

希尔排序是直接插入排序的一种优化
稳定性：不稳定
时间复杂度：O(N) ~ O(N ^ 2)
空间复杂度：O(1)

直接选择排序

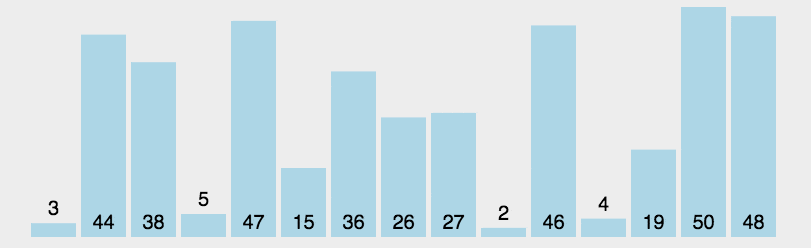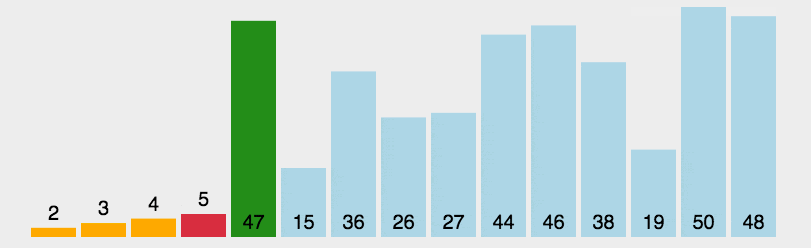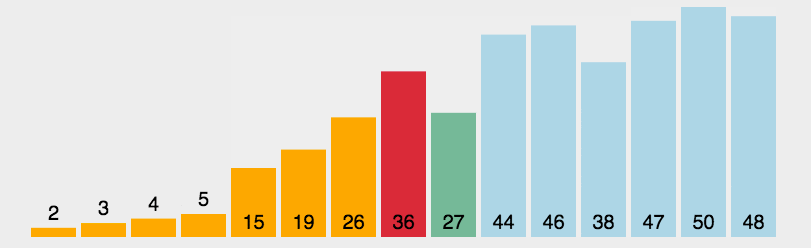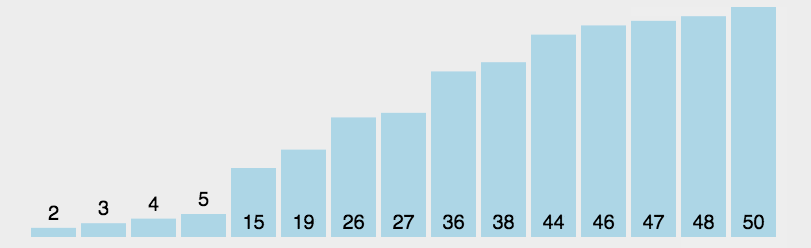
思想：每次从待排序数据元素中找到最小或最大的一个元素，放在待排序的起始位置，直到全部都排完
实现：遍历整个待排序列，记录当前下标i，再遍历其后面的元素，判断是否有比它小的，如果有记录当前下标，然后进行交换

public class Test {public static void main(String[] args) {int[] array = {3,1,2,3,4};selectSort(array);System.out.println(Arrays.toString(array));}//选择排序public static void selectSort(int[] array){for (int i = 0; i < array.length; i++) {int minIndex = i;for (int j = i+1; j <array.length ; j++) {if(array[j]<array[minIndex]){//记录最小元素下标minIndex=j;}}//进行交换swap(array,i,minIndex);}}public static void swap(int[] array,int i,int j){int tem = array[i];array[i] = array[j];array[j] = tem;}
}

时间复杂度：O(N^2)
空间复杂度：O(1)
稳定性：不稳定

堆排序

思想：就是利用堆这种数据结构进行排序
大根堆：用于排升序序列
小根堆：用于排降序序列

思路：以排升序为例
1.先将其数组创建为大根堆
2.定义一个end表示最后一个元素下标，每次堆顶元素都是最大的，将堆顶元素和堆底元素交换，将end–，相当于将堆底元素删除，这时就还要重新向下调整为大根堆
3.直到end为0的时候截止

public class Test {public static void main(String[] args) {int[] array = {3,1,2,3,4};heapSort(array);System.out.println(Arrays.toString(array));}//堆排序//从小到大，就使用大堆，每次把最后一个元素确定public static void heapSort(int[] array){//创建大根堆creatHeap(array);//每次将最后一个与第一个交换int end = array.length-1;while(end>0){swap(array,0,end);siftDown(array,0,end);//去掉最后一个从新排序end--;}}//建立大根堆堆private static void creatHeap(int[] array) {//从最下面的父亲节点开始调整for (int parent = (array.length-1-1)/2; parent >=0 ; parent--) {siftDown(array,parent,array.length);}}//向下调整private static void siftDown(int[] array, int parent, int length) {int child = 2*parent+1;while (child<length){if(child+1<length&&array[child]<array[child+1]){child++;}if(array[child]>array[parent]){swap(array,child,parent);parent = child;child = 2*parent+1;}else{break;}}}public static void swap(int[] array,int i,int j){int tem = array[i];array[i] = array[j];array[j] = tem;}
}

时间复杂度：O(N*logN)，调整堆O(logN)，需要遍历整个数组，每次可能都要调整堆
空间复杂度：O(1)
稳定性：不稳定

冒泡排序

冒泡排序（Bubble Sort）是一种简单的排序算法，它通过重复地遍历待排序的列表，比较相邻的元素并交换它们的位置来实现排序。每遍历一次就确定一个最后一个元素

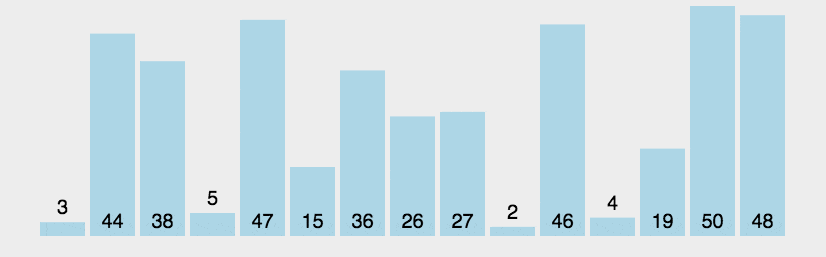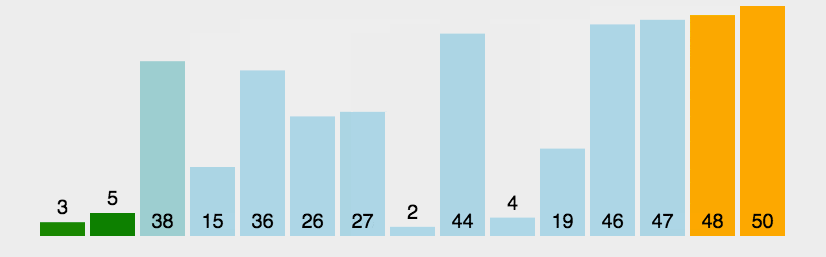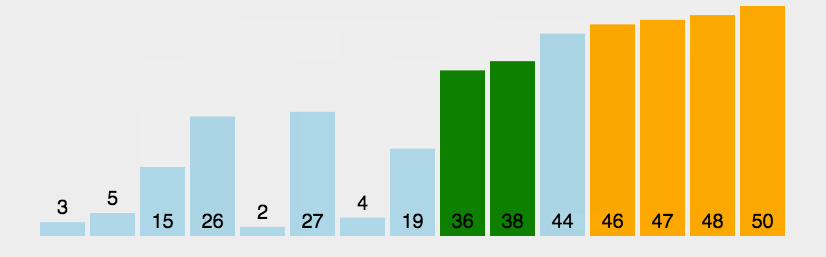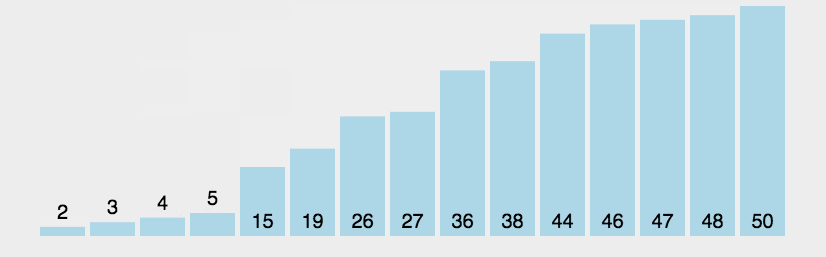
public class Test {public static void main(String[] args) {int[] array = {3,1,2,3,4};bubberSort(array);System.out.println(Arrays.toString(array));}public static void bubberSort(int[] array){//外层确定比较几趟/for (int i = 0; i < array.length-1; i++) {//内层确定每趟比较次数for (int j = 0; j < array.length-i-1; j++) {if(array[j]>array[j+1]){int tem = array[j];array[j] = array[j+1];array[j+1] = tem;}}}}
}

快速排序

快速排序（Quick Sort）是一种高效的排序算法，使用的是分治法的思想
就是找到一个基准值，将列表分为两部分，左边一部分是小于基准值，右边一部分是大于基准值，分别在此基准值的左边和右边，重复同样的操作
因此这里可以是使用递归来写的

1.通常以第一个为基准值，然后进行调整左右
2.递归其这个基准值下标左边 和 右边 ，直到左边下标>=右边下标就结束递归
3.这里找到基准值使用Hoare方法来来进行调整，就是high下标先从右向左找到比基准值小的值，low下标从左向右找到比基准值大的值，进行交换，low >= high ，就说明结束了，将此时的low下标与基准值进行交换

public class Test {public static void main(String[] args) {int[] array = {3,1,2,11,4};QuickSort(array);System.out.println(Arrays.toString(array));}//快速排序public static void QuickSort(int[] array){Quick(array, 0, array.length-1);}public static void Quick(int[] array,int left,int right){//截止条件if(left>=right){return;}//递归，先将其以key为界限分为两组//key左右两边又可以分组int key = Hoare(array,left,right);Quick(array,left,key-1);//递归左边Quick(array,key+1,right);//递归右边}//调整基准值位置，并返回其下标private static int Hoare(int[] array, int low, int high) {int i = low;int tem = array[low];while (low<high){//1.后面找到比前面基准值小的while (low<high&&array[high]>=tem){high--;}//2.从前面找比基准值大的while (low<high&&array[low]<=tem){low++;}//2.交换swap(array,low,high);}//与基准值进行交换swap(array,i,low);return low;}public static void swap(int[] array,int i,int j){int tem = array[i];array[i] = array[j];array[j] = tem;}
}

上面是使用的是Hoare方法来调整其列表

当然这里也可以使用挖坑法
挖坑法：就是先定义一个临时变量来存放我们的基准值
1.先从后向前找high下标一个小于临时变量的值，将这个值放入放入low下标
2.从前向后找low下标一个大于临时变量的值，将这个值放入high下标地方
重复操作，直到low>=high就结束，最后将low下标的值修改为tem基准值

这里调整基准值方法不仅可以使用Hoare方法，这里也可以使用挖坑法
1.先将基准值拿出来
2.先从后向左找一个小于基准值的值放入坑中，此时该位置就便相当于为坑
3.在从左向右找一个大于基准值的值放入坑中, 此时该位置就便相当于为坑

//挖坑法private static int parttion(int[] array,int low,int high){int tem =array[low];while (low<high){while (low<high&&array[high]>=tem){high--;}array[low] = array[high];while (low<high&&array[low]<=tem){low++;}array[high] = array[low];}array[low] = tem;return low;}

快速排序优化：三数取中
比如序列：1 2 3 4进行快速排序，这样会使其时间复杂度为N^2,因为其快速排序像构建二叉树一样，这样会浪费时间，因此可以使用一个方法
将low 、mid 和 high下标的值其中最中间的值作为基准值

上面找基准值就是找其第一个元素，但有时候第一个元素并不是最好的，所以可以找第一个、中间、最后一个其中中间的值，作为基准值这样更合理

//这里利用三数取中，获取其三个钟最中间元素的下标private static int mid(int[] array, int low, int high) {int mid = (low+high)/2;if(array[low]<array[high]){if(array[mid]<array[low]){return low;}else if(array[mid]>array[high]){return high;}else {return mid;}}else{if(array[mid]<array[high]){return high;}else if(array[mid]>array[low]){return low;}else {return mid;}}}

时间复杂度：O(N * log N) ~ O (N ^2)，因为每次进行基准值调整就像在构建一颗完全二叉树，构建数的复杂度为log N
这里又要重复N次 ，但是如果其数列有序的话，时间复杂度可能为O (N ^2)
空间复杂度：O(log N)，因为底层就像一颗二叉树
稳定性：不稳定

快速排序非递归形式
这里采用非递归，但是还是要使用挖坑法或者Hoare 方法进行基准值调整
这里是使用stack进行操作，这里如果符合条件就将其下标入栈，缩小其基准值调整范围，一部分一部分调整，不断的将下标入栈和出栈操作，当栈为空的时候就结束了

public class Test {public static void main(String[] args) {int[] array = {3,1,2,11,99,33,22,11,4,7,8};quickSortNor(array);System.out.println(Arrays.toString(array));}//快速排序非递归public static void quickSortNor(int[] array) {int start = 0;int end = array.length-1;int par = parttion(array,0,end);Stack<Integer> stack = new Stack<>();if(par>start+1){stack.push(start);stack.push(par-1);}if(par<end-1){stack.push(par+1);stack.push(end);}while (!stack.isEmpty()){end = stack.pop();start = stack.pop();par = parttion(array,start,end);if(par>start+1){stack.push(start);stack.push(par-1);}if(par<end-1){stack.push(par+1);stack.push(end);}}}private static int parttion(int[] array,int low,int high){int tem =array[low];while (low<high){while (low<high&&array[high]>=tem){high--;}array[low] = array[high];while (low<high&&array[low]<=tem){low++;}array[high] = array[low];}array[low] = tem;return low;}
}

运行结果如下

归并排序

归并排序（Merge sort）就是采用分治法将其分为子序列，先将子序列变为有序，在将子序列归并进行排序，最终整体就有序了

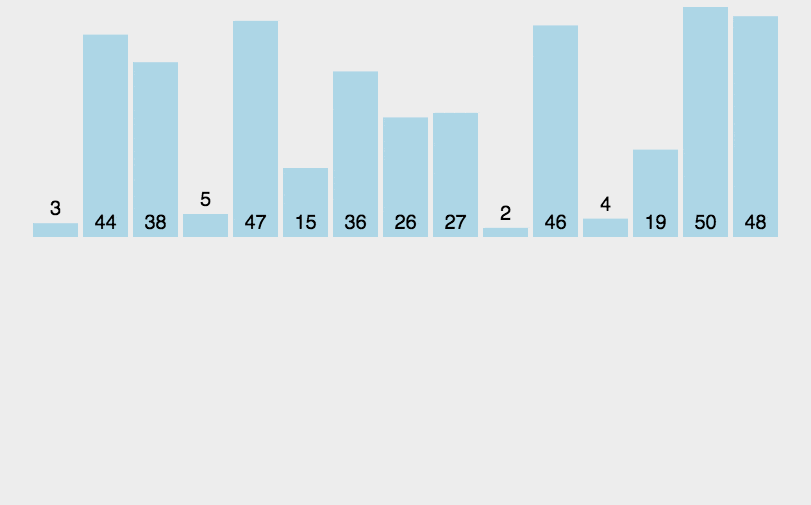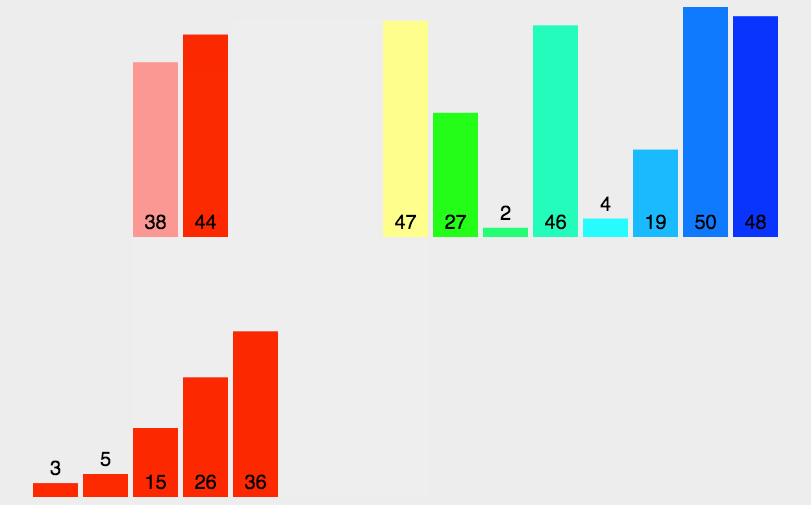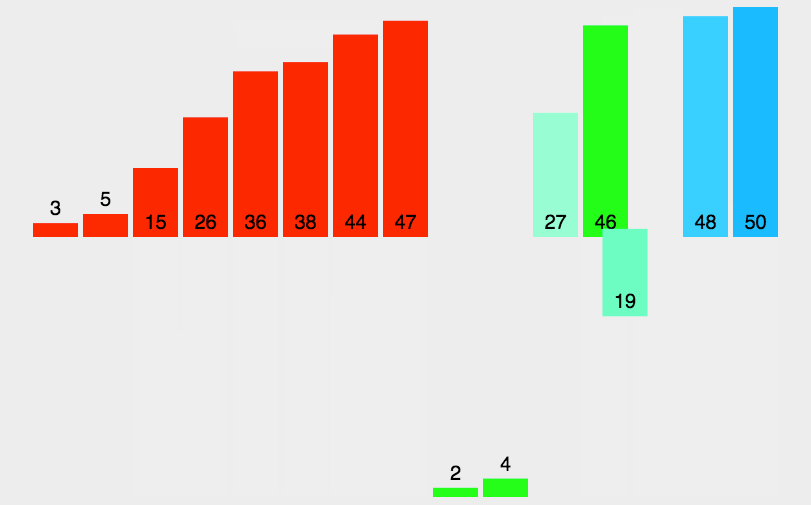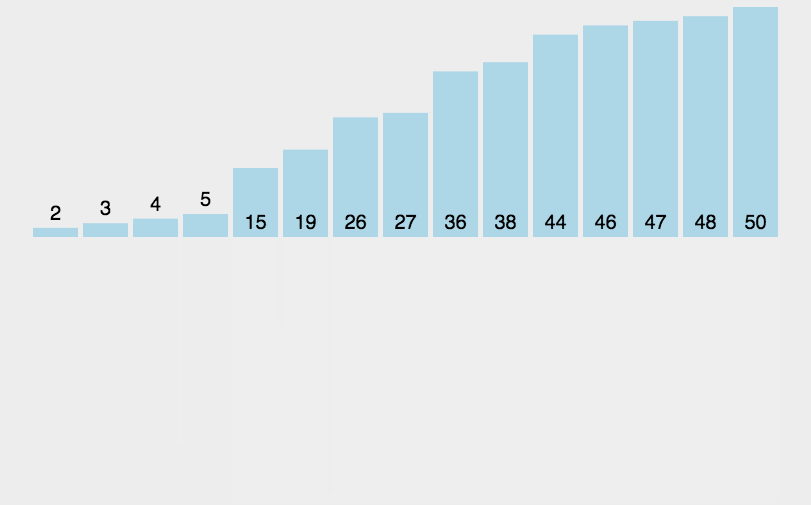
就是分解和合并两个操作
先将其分解到不能分解，合并过程中并且注意合并成是有序的数列，就这样一直和并子序列，最后整体的序列就有序了

public class Test {public static void main(String[] args) {int[] array = {3,1,2,11,4,7,8};mergeSort(array);System.out.println(Arrays.toString(array));}//归并排序public static void mergeSort(int[] array){mergeSortChild(array,0,array.length-1);}//使用递归实现private static void mergeSortChild(int[] array, int left, int right) {if(left>=right){return;}//每次将其分为两部分进行排序int mid = (left+right)/2;//递归左边mergeSortChild(array,left,mid);//递归右边mergeSortChild(array,mid+1,right);//合并merge(array,left,mid,right);}//合并private static void merge(int[] array,int left,int mid,int right){int tem[] = new int[right-left+1];int k = 0;int s1 = left;int e1 = mid;int s2 = mid+1;int e2 = right;//将这两个合并成一个有序数组while (s1<=e1&&s2<=e2){if(array[s1]<=array[s2]){tem[k++] = array[s1++];}else {tem[k++] = array[s2++];}}//最后将另一个没有放进去的放进去while (s1<=e1){tem[k++] = array[s1++];}while (s2<=e2){tem[k++] = array[s2++];}//最后将这个合并好的放入array数组中for (int i = 0;i<tem.length;i++){array[i+left] = tem[i];}}
}

运行结果如下

时间复杂度：O(N*log N)，和快速排序一样
空间复杂度：O(N)
稳定性能：稳定

计数排序

上面的排序都是不断的进行比较移动进行排序，而计数排序是非比较型
1.他就是通过数组下标来存放对应的值，如果这个值和某个下标相同，就将该下标的对应的值++，相当于用一个count数组来记录每个数出现的次数放在对应下标上
2. 全部放完以后，循环这个count数组，如果对应count[i] ! = 0 ，说明此下标存放值了，就将下标放入array数组中

注意这里再对应下标存放的时候，可能出现92  -  99这样范围的序列
因此这里再存放的时候下标可以减去最前面的值，下标-92，将这个作为下标
最后取出放入array数组的时候，要加上92

public class Test {public static void main(String[] args) {int[] array = {3,1,2,11,4,7,8};countSort(array);System.out.println(Arrays.toString(array));}//计算排序public static void countSort(int[] array){int min = array[0];int max = array[0];//1.获取其最大值和最小值for (int i = 1; i < array.length; i++) {if(array[i]>max){max = array[i];}if(array[i]<min){min = array[i];}}//确定数组长度//在对应下标存放于下标相同的值int range = max - min + 1;int[] count = new int[range];for (int i = 0; i < array.length; i++) {//将array[i]对应的值为count的下标，遇到就++int index = array[i];//这里之所以要减去min，是因为这里可能出现越界问题//如果是92 - 99的值，但是下标并不是这样的,减去最前面的值count[index-min]++;}int k = 0;for (int i = 0; i < count.length; i++) {while (count[i]!=0){//由于前面下标减去一个min,这里要加回来array[k] = i+min;count[i]--;k++;}}}
}

时间复杂度：O(n + k)，n是列表长度，k是数据范围
空间复杂度：O(n + k) ，需要额外的计数数组和结果数组

排序方式	最好	最坏	空间复杂度	稳定性
冒泡排序	O(N^2)	O(N^2)	O(1)	稳定
插入排序	O(N)	O(N^2)	O(1)	稳定
选择排序	O(N^2)	O(N^2)	O(1)	不稳定
希尔排序	O(N)	O(N^2)	O(1)	不稳定
堆排序	O(N*logN)	O(N*logN)	O(1)	不稳定
快速排序	O(N*logN)	O(N^2)	O(logN~N)	不稳定
归并排序	O(N*logN)	O(N*logN)	O(N)	稳定